基于半实物仿真的组合导航系统抗侧风设计*

陈 沣,杨鹏翔,刘梦焱,刘 琴,梅春波,郭昊昌

(西安现代控制技术研究所, 西安 710065)

0 引言

随着小型无人机体积、成本的下降,基于MEMS惯性器件的捷联惯性导航系统(SINS)、卫星导航系统(GNSS)进行的组合导航得到了广泛应用。但是在无人机平直飞行过程中,SINS/GNSS航向可观测性较差[1],低精度MEMS惯导无法保证长时间航向测量精度。文献[2]提出了一种磁强计组合方法,但是适用于小型无人机体积的磁强计大多需要标定,且容易受其他电子部件干扰,很难达到规定精度。文献[3]讨论了一种通过动力学模型以及惯性导航输出量估计攻角及侧滑角的方法,估计精度较高,但是需要精确的模型以及气动力的输入,在缺乏大气测量器件的情况下不可行。文献[4]、文献[5]提出了用GNSS位置、速度推算航向角的方法,在无风理想条件下取得了良好的效果,但是在有侧风条件,由于侧滑角的影响,航向角估计精度变差,而且会影响俯仰角精度。

在速度修正航向的基础上,文中以MEMS SINS/GNSS组合导航系统[5]为平台,设计了一种侧滑角在线估计与补偿方法。利用半实物仿真进行验证,结果表明,在侧风条件下,算法可有效提高组合导航系统的姿态角精度;无风条件下,姿态角精度亦不损失。

1 组合导航方案设计

1.1 序贯卡尔曼滤波方程建立

线性条件下,系统的状态方程和量测方程的简化形式为[6]：

(1)

Zk=HkXk+Vk

(2)

式中:Xk、Zk、Hk、Vk、Wk-1分别为tk时刻系统状态、量测值、量测距阵、量测噪声序列、系统噪声序列;Φk/k-1为tk-1时刻至tk时刻的一步状态转移矩阵;Γk-1为tk-1时刻系统噪声驱动矩阵。

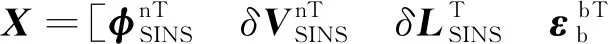
(3)

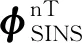
时间更新迭代方程如下：

状态一步预测[6]：

(4)

一步预测均方误差[6]：

(5)

式中,Qk-1为系统噪声协方差阵[7]。

量测更新采用序贯方式处理。量测更新方程为：

ZP,k=LSINS-LSAT

(6)

ZV,k=VSINS-VSAT

(7)

式中：ZP,k、ZV,k分别为tk时刻位置、速度量测值;LSINS、VSINS分别为惯性导航解算得到的位置、速度;LSAT、VSAT分别为卫星导航输出的位置、速度。

位置、速度量测的滤波增益均可表示为[6]：

(8)

其中,R为量测噪声协方差阵。

状态估计[6]：

(9)

均方误差[6]：

Pk/k=(I-KkHk)Pk/k-1

(10)

1.2 航向量测分析

在无水平机动的情况下,航向角观测性较差,故组合导航在平直运动时利用卫星导航相对地面的速度航向纠正航向角。

俯仰、滚转角较小时,近似认为速度矢量在水平面投影方向Ψtr与航向角Ψ误差为侧滑角β。

航向量测量[6]：

Zyaw,k=βk=Ψtr-Ψ

(11)

航向量测的滤波增益为：

(12)

式中:航向量测阵Hyaw=[0 1 001×12];Ryaw为量测噪声协方差阵,可认为航向噪声幅度为2°～6°。

均方误差[6]：

Pk/k=(I-Kyaw,kHyaw,k)Pk/k-1

(13)

状态估计[6]：

(14)

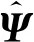
图1 速度增加量失准角示意图

在速度量测更新过程中水平速度误差会传递到俯仰、滚转误差角中,造成错误的姿态角修正,位置量测更新中也会出现类似现象。

由于存在以上误差,组合导航系统需要尽量减少航向失准角,同时减少航向失准角对于速度、位置量测的影响。

1.3 速度航向H∞滤波

由于速度量测对于姿态角影响较为显著,采用鲁棒性更好的H∞滤波进行速度量测,位置量测仍然采用标准卡尔曼滤波量测更新。

在随机线性离散系统中,H∞滤波算法递推公式可以表示为[8]：

(15)

其中,Lk为线性矩阵,这里取为单位阵。为调节鲁棒性和精度的因子,当γ→∞时H∞滤波就退化为Kalman 滤波[9]。γ越大系统精度越高,但鲁棒性降低,这里取为30。

1.4 侧滑角估计

由于转弯过程中航向角误差可观测性增加,初始航向误差会逐渐减小。所以载体转弯过程中,停止航向量测更新。转弯结束,滚转角及俯仰角均小于10°后,可以认为航向误差收敛到最小,且载体纵向对称平面近似垂直于地面。根据载体航迹特性,等待一定时间,并进行平滑滤波。

平滑后的侧滑角为：

βm=Ψtr,m-Ψm

(16)

其中,Ψtr,m为转弯结束后tm时刻速度矢量在水平面投影,Ψm为转弯结束后tm时刻航向角。

则航向量测量变为：

Zyaw,k=Ψtr,k-βm

(17)

其中,Ψtr,k为下次转弯开始前的tk时刻速度矢量在水平面投影方向。速度、位置量测更新后进行类似式(8)～式(10)的航向量测更新,以修正平直飞行过程中天向陀螺造成的航向漂移。每次转弯结束后,更新一次βm。

2 半实物仿真环境设计

为了验证组合导航算法在物理平台中的性能,搭建了半实物仿真环境进行验证。仿真系统框图如图2所示。仿真机控制转台运行,根据载体数学模型生成载体的加速度以及比力,注入到组合导航系统中。组合导航系统安装在三轴转台上,敏感转台转动角速率,同时接收卫星模拟器发射的卫星信号以及仿真机注入的比力数据,进行组合导航解算。组合导航系统输出的姿态角、速度、位置信息又送回到仿真机参与控制模型解算与弹道动力学方程解算。

图2 半实物仿真系统框图

控制模型接收导航输入的姿态角、速度、位置,进行爬升控制、航线控制、高度控制等中制导控制策略,输出舵偏角δ。

仿真机由舵偏角δ可以得出滚动、偏航、俯仰力矩Mx、My、Mz,并由质心转动方程解出载体系下转动角速率[10]：

(18)

其中,Jx、Jy、Jz为载体系下转动惯量,ωf为仿真机计算的载体系下角速率。

仿真机可以由式(19)解出姿态角[10]：

(19)

位置、速度的计算,仿真机转入弹道坐标系处理。载体的质心动力学方程为[10]:

(20)

其中,Fd为弹道坐标系下载体受到的外力,可以由推力、载体气动参数等得出。V、θv、Ψv分别为仿真机计算载体的速度、弹道倾角、弹道偏角。

Fd转到载体坐标系下为Fb。在载体质量m已知的情况下,可计算出载体系下加速度ab,转换到导航系下为an。

导航系比力为：

(21)

进而得到载体系下比力fb。fb由仿真机注入到组合导航系统中,以模拟组合导航装置的线运动。

质心运动的动力学方程为[10]：

(22)

其中,x、y、z为弹道坐标系下位置。

弹道坐标系下的速度、位置输入到卫星信号模拟器中,模拟器可以模拟载体的卫星导航信号,发送给组合导航系统。

组合导航输出的姿态、速度、位置,与仿真机输出姿态、速度、位置转到同一坐标系下比较,即可得出组合导航误差。

3 组合导航系统的半实物仿真试验

仿真系统选用的低精度MEMS SINS,陀螺零位偏差约为300°/h,刻度系数重复性小于5%。卫星接收机定位误差小于10 m,速度误差小于0.5 m/s。安装误差角小于0.3°。

飞行轨迹如图3所示。

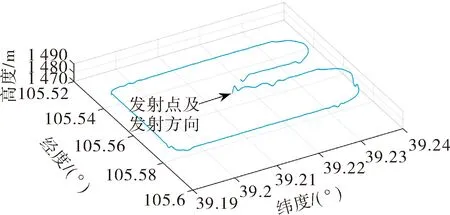
图3 飞行轨迹

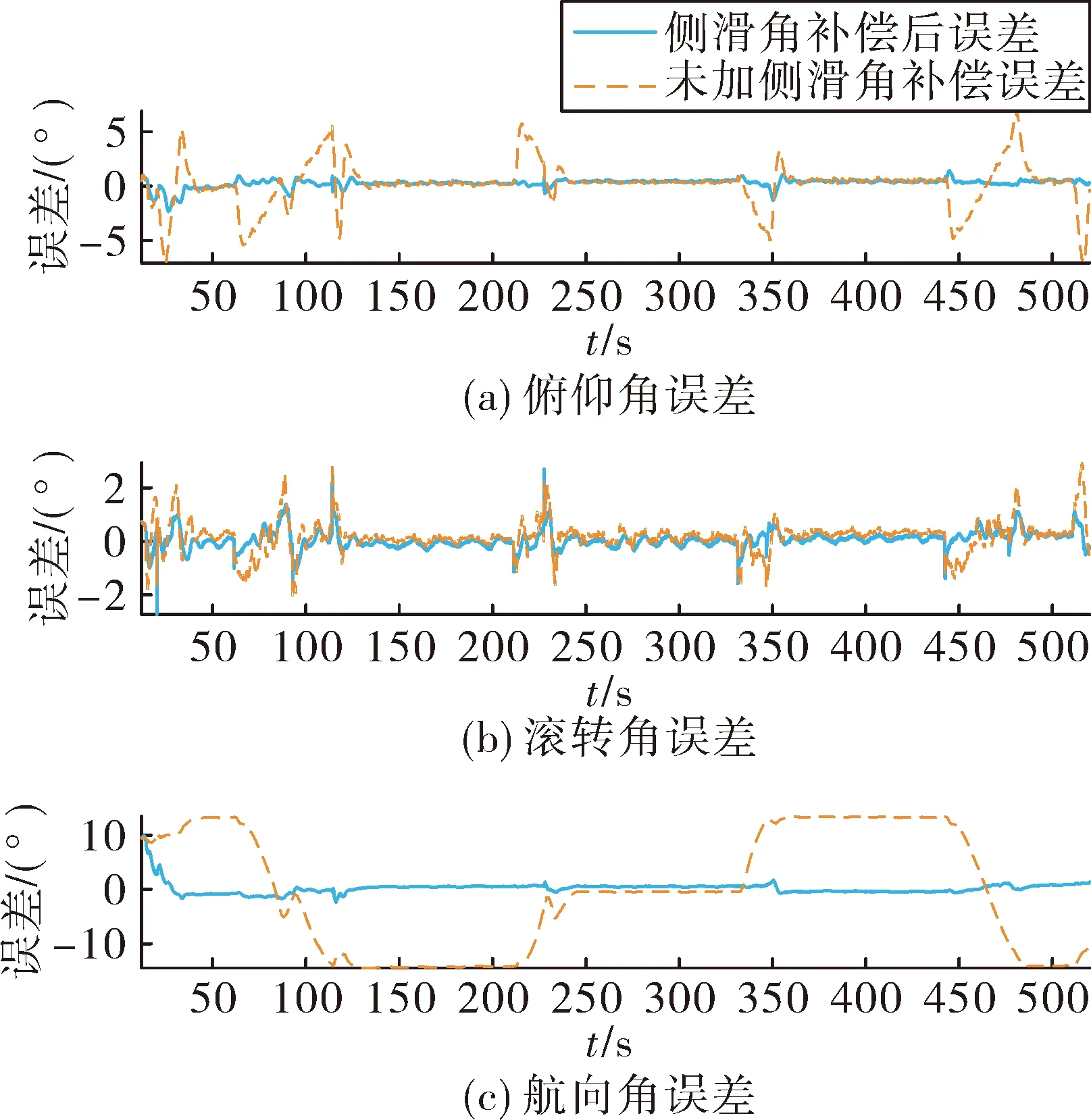
图4 姿态角误差曲线

风力条件侧向10 m/s,方向由西向东时,侧滑角补偿前后误差曲线如图4所示。分别比较不同侧风条件下,两种方法姿态角误差,如表1所示。姿态角误差为组合导航系统输出姿态角与转台姿态角作差得到。位置、速度误差为组合导航输出与仿真机输出求差得到,具体数值见表1。

表1 误差统计表格(RMS)

如表1所示,侧滑角补偿方法在3种条件下误差分布较为平均：在无风条件下比未补偿方法误差偏大;但是在6 m/s侧风及10 m/s侧风条件下,航向角误差有显著改善,且俯仰角误差改善也较为明显。同时,速度、位置误差没有显著增加。

4 结论

应用抗侧风侧滑角估计方法后,增加了航向角解算中天向陀螺的权重,增加了速度量测的鲁棒性,降低了速度方向对航向角修正的作用。所以相对于全程用速度方向修正航向角的方法,侧滑角估计方法在无风条件下误差稍大,但是在有侧风条件下,由于航向失准角较小,航向角、俯仰角误差显著降低。小型无人机飞行速度慢,在飞行过程中较容易受到侧风影响,所以在实际飞行中侧滑角估计方法的姿态角误差更小。