平面复合连杆机构设计及可动性分析

张 春，胡小春，林佳裔

（合肥工业大学机械工程学院，安徽 合肥 230009）

1 引言

平面连杆机构是由若干刚性构件通过低副联接而成，低副的制造成本较低，接触面积大，承载能力较强，在送料机、冲床、内燃机、压缩机、鹤式起重机等各类机械中得到广泛应用[1]。平面四杆机构的设计研究已经取得丰硕的成果，对于平面五杆机构的设计研究有待完善，平面四杆和五杆复合机构的研究甚少。

平面连杆机构的常见设计方法有同源机构法、矢量环方程法、矩阵约束法。文献[2]利用数值图谱法进行曲柄滑块机构连杆轨迹的尺度综合，并探讨同源机构在尺度综合中的应用。文献[3]利用胚图插点的方法分析了平面两自由度五杆、七杆、九杆机构。文献[4]根据连杆机构基本尺寸与其转角函数的关系，建立了连杆曲线数值图谱，以及推导了连杆机构实际尺寸、连杆上点的位置和安装尺寸参数理论公式。文献[5]以平面可调五杆机构为研究对象，利用机构的闭环矢量方程，运用SIMULINK进行机构运动学分析。文献[6]通过分析齿轮五杆曲柄滑块机构的尺寸约束条件，利用复矢量理论和Fourier级数理论建立了机构连杆轨迹的数学模型。文献[7]根据五杆机构的装配条件，研究了五杆机构双曲柄存在的充要条件。文献[8]采用拆运动链法分析了平面铰链五杆机构曲柄存在的条件。文献[9]应用“杆组法”研究了含RPRⅡ级杆组的双自由度五杆机构双曲柄存在的充要条件。文献[10]通过研究两自由度多环混合驱动机构的可动性分析，提出了适用于多自由度多环混合驱动机构可动性分析的方法。文献[11]将单环运动链的可动性条件与其工作空间相结合，分析、求解平面多环、多自由度机构可动性。文献[12]根据机构输入输出的速度Jacobian矩阵，提出了求解平面多环多自由度机构奇异位形的一般方法。文献[13]分析了闭环机构运动时所存在的各种奇异性。文献[14]分析了四个三自由度对称零扭矩并联机构的奇异性。

利用解析法和矢量环方程法设计平面四杆和五杆滑块复合机构，运用Grashof法则分析并得到复合机构的杆长关系，根据机构的位置矩阵和速度矩阵分析符合机构的各种奇异性。

2 机构设计

2.1 曲柄滑块机构设计

曲柄滑块机构在刨床、冲床、压缩机等各类机械有着广泛应用。曲柄滑块机构常用的设计方法有作图法、解析法、同源机构法、矢量环方程法、矩阵约束法等。采用解析法设计曲柄滑块机构。

已知曲柄滑块机构的行程速比系数K、最大行程S、偏心距e，确定该机构曲柄长度u和连杆长度x的尺寸，如图1所示。图中：C1和C2—滑块的极限位置；S—距离；兹—该机构的极位夹角。

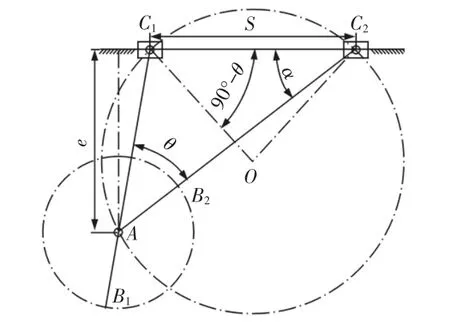
图1 曲柄滑块机构设计简图Fig.1 Design Sketch of Slider Crank Mechanism

平面四杆机构的行程速比系数表达式为：

所以平面四杆机构的极限夹角表达式为：

∠C1AC2为机构的极限夹角。在驻OC1C2中，∠C1OC2=2∠C1AC2=2兹，所以：

在 驻AC1C2中：

根据式（3）和式（5），推导得到琢表达式为：

由式（1）～式（6），可推导出曲柄和连杆的长度参数 u，x，其表达式如下：

2.2 五杆滑块机构设计

随着机械产品的发展，平面五杆机构被广泛地应用，如串联式机器人和机械臂；其常用设计方法：同源机构法、矢量环方程法、矩阵约束法等。因平面五杆机构具有2个自由度，将五杆滑块机构与曲柄滑块机构采用复合方式降低机构自由度，如图2所示。

矢量环方程法是设计平面铰链机构的有效方法，但对于复合机构和五杆滑块机构涉及较少。采用矢量环方程法设计复合机构中五杆滑块机构的公共连杆CD长度y和连杆DE长度z，其机构简图，如图3所示。

图3 机构简图Fig.3 Schematic Diagram of Mechanism

曲柄从B位置运动到Bi位置的机构简图，如图3所示。ABCCiBiA和EDCCiDiEiE分别组成封闭的矢量环，因此可列出方程：

式中：j—虚数单位；兹1i—曲柄AB到达ABi位置所旋转的角度；兹2i—三角形BCD到达BiCiDi所旋转的角度；兹3i—杆件DE到达DiEi所旋转的角度。

由式（8）可推导出：

当给定复合机构中AB和BC转角兹1i、兹2i和DE转角兹3i和滑块运动矢量di棕的三个运动位置，由克莱姆法则得到DE和CD矢量z和y，其表达式为：

3 复合机构的可动性分析

五杆滑块机构（如图4所示）是平面铰链五杆机构（如图5所示）演化而成，其演化原理与曲柄滑块机构的演化机理一致。所设计的五杆滑块机构只能存在单曲柄，所以演化后的平面铰链五杆机构只存在一个曲柄。

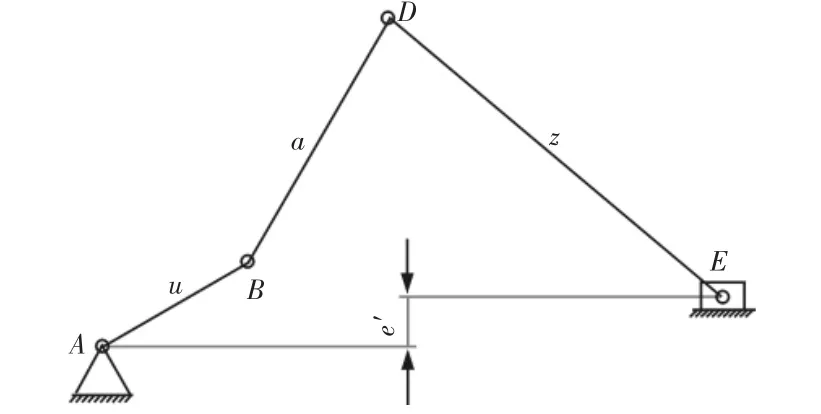
图4 五杆滑块机构简图Fig.4 Sketch Diagram of Five-Bar Slider Mechanism

图5 平面五杆机构简图Fig.5 Sketch of Planar Five-Bar Mechanism

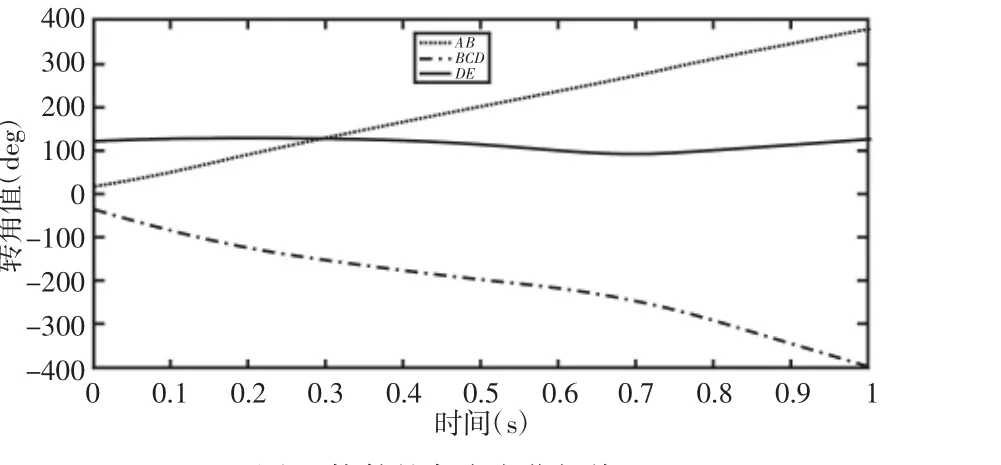
根据演化过程可得到lg=∞，ls=∞+e′，所以ls是最长杆长。l为u，a，z中的最大值，m+n=u+a+z-l。根据格拉斯霍夫准则[15]可知：当平面铰链五杆机构满足ls+m+n

当u

当该机构中a

4 复合机构的奇异性分析

机构奇异性关系到机构稳定性和安全性；机构发生奇异时，机构不稳定、不可控、机构特性较差。根据机构的位置约束方程：F（兹，f）=0可以推导得到速度矩阵Af˙+B兹˙＝0，当det（A）=0或det（B）=0时，机构将产生奇异性，f和兹分别表示输入参数和输出参数。

根据机构正向运动学分析可推导出：

根据式（14）可推导出复合机构中曲柄滑块机构的速度矩阵，其表达式可表示为：

根据机构产生奇异的条件并结合式（15）可知：cos兹2=0或sin（兹2-兹1）=0。由于 u≠x，所以曲柄滑块机构产生奇异的条件为：兹1=此时机构瞬间增加自由度。

根据式（14）可推导出复合机构中五杆滑块机构的速度矩阵，其表达式可表示为：

根据机构产生奇异的条件并结合式（16）可知：cos兹3=0或sin时，此时五杆滑块机构正逆向运动学同时产生奇异；当 兹2+琢＝兹1或 兹2+琢＝兹1+π 时，此时五杆滑块机构逆向运动学产生奇异，机构瞬间减少自由度。

5 实例

根据上述的设计方法，设计出平面四五杆滑块机构的设计尺寸，其尺寸参数，如表1所示。通过计算机仿真，机构运动过程中构件角度变化规律，如图6所示。

表1 实例机构的设计尺寸（单位：mm）Tab.1 Example Mechanism of Design Dimensions

图6 构件的角度变化规律Fig.6 Angle Change Law of Component

6 结论

根据图1所示曲柄滑块机构杆件参数的几何关系，推导得到曲柄滑块机构中曲柄参数连杆参数的解析表达式；由图3所示复合机构并利用矢量环方程法推导得到五杆滑块机构的杆件参数；根据复合机构的装配条件和格拉斯霍夫准则，分析得到机构存在曲柄的条件；根据该复合机构的正向运动学推出该机构的位置矩阵和速度矩阵，分析得到该机构产生奇异的位置。