轮履复合移动平台连杆切换机构的设计分析
2020-03-28杜忠华尚宇晴
王 腾,杜忠华,谢 磊,尚宇晴
(南京理工大学机械工程学院,江苏 南京 210094)
1 引言
在城市废墟搜救和工程探险勘测、反恐防暴、军事侦察、星球探测[1]等复杂环境下事件的应对中,人员的伤亡十分严重,为实现机器人代替执行高危任务的目的,各国日益重视对无人战车的研究。目前的无人战车存在的问题主要是:履带式平台拥有很强的地面通过性和环境生存力,但机动灵活不足,响应迟缓;轮式平台机动灵活,反应快速,但地面通过性和环境适应性差。所以轮-履复合是移动平台研究的热点与趋势[2-4]。目前轮履复合最常见的方式是一平台同时安装轮式和履带式机构,在不同的场合使用相应的行走机构,如美国的Andros移动平台[5]和沈阳自动化研究所“灵蜥”反恐防暴移动平台[6];但大多此类移动平台并没有实现轮、履的彻底切换,不能实现纯轮、纯履的运动;或者明显偏重一方,另一方只起辅助作用。另一种方式为模块化可更换形式,即针对不同环境,需要进行轮、履人为更换,国内外普遍通用一种三角履带总成[7];这大大削弱了平台的自主性,无法满足战场需求。第三种为基于变胞原理的复合方式,根据环境变化、任务需求,平台进行自我重组和重构。如Viper移动平台采用的以色列Galileo公司研制的轮履复合式底盘[8],此类平台内部结构较为复杂,控制困难,可靠性差。针对以上讨论,提出的轮履复合移动平台,通过关节式切换机构实现轮、履的组合与彻底转换。既克服了履带式作战平台机动灵活不足,响应迟缓的缺点,又解决了轮式作战平台地面通过性和环境适应性差的问题。而且自主性高,既能满足实战要求、又控制可靠。
2 系统组成
移动平台的结构布局,如图1所示。整体看,履带模块设置在车体的两侧,形似车体的肋部位置,轮子安装在车桥(包括前桥和后桥)上,形似车体的四肢部位。关节式轮履切换机构设置在车体内部的四角方位,车桥再通过切换机构安装在车体上。如此布局,履带前后轮与车体刚性连接,跨越壕沟、越障和承载能力更强。车轮采用四驱的模式,能够实现平台灵活运动和差速转向,动力性好。现有的轮履复合移动平台研究中对悬架的研究不多,普遍较为简陋,功能不全。本研究自主设计的主、被动结合的悬架能够主动调整车桥相对地面的位置高度,既做到轮履切换又实现爬坡越障;主动悬架与切换机构一体化设计。被动悬架下挂弹性元件、导向机构以及减震器,能够补偿四个轮子之间的离地高度差。保障平台行走的平顺。
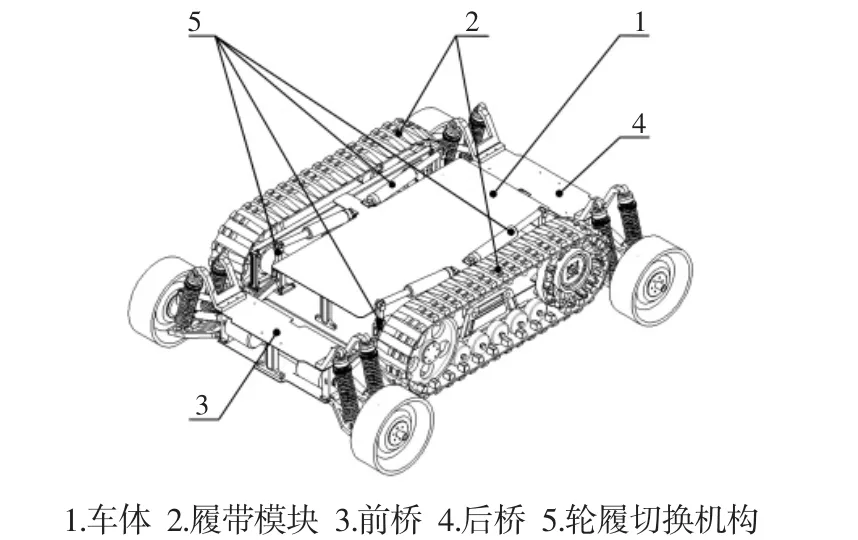
图1 移动平台结构布局Fig.1 Robot Structure Layout
移动平台具有轮式和履式两种运动模式,轮型模式,如图2(a)所示。适用于平坦路面,实现快速前进、转弯、后退,灵活迅速、机动性高;履带模式,如图2(b)所示。附着力大,通过性好,用于爬坡越障、跨越壕沟,任意地形下平稳前进;移动平台还可以实现不完全切换,如图2(c)所示。应对特殊场合,如在翻越台阶时,采用车前轮先抬起登上台阶,车后轮着地,使履带保持一定高度,辅助翻越的策略。这种方式使得平台的质心更容易攀越台阶的外角线。

图2 移动平台运动模式及姿态Fig.2 Robot Movement Pattern and Attitude
3 轮履切换机构设计
3.1 基本构成
轮履切换机构是设计的核心,如图3所示。切换机构单个模块由一个电缸,一个固定座,若干连杆和若干根销轴组成,各连接处通过销轴铰接,由电缸驱动。

图3 轮履切换机构结构示意图Fig.3 Structure Diagram ofthe Wheel-Track Switching Mechanism
3.2 工作原理
行走方式由履带式向轮式切换时,电缸5的推杆伸出,推动摆动杆1绕A点转动,摆动杆1带动连杆2旋转,连杆2推动悬臂杆3带动车桥落下。推杆完全伸出后,摆动杆1正好竖直,与连杆2重叠,同时悬臂杆3上限位块抵住连杆2,使得连杆2前有限位块抵住,后因推杆推住,前后都不能转动。此时连杆机构锁死。地面传递给轮子的力最终由连杆2在竖直方向承受,推杆只是在侧边抵住,保持结构不变,几乎不受力,避免了震动可能对电缸造成的损伤。
行走方式由轮式向履带式切换时,电缸5推杆缩回,运行顺序相反,切换终止后,应避免摆动杆1与电缸5共线,停留在死点位置,出现下一轮切换锁死现象。
3.3 运动学分析
轮履切换机构为五杆机构,杆EF为伸缩驱动杆,机构简化运动学模型,如图4所示。图中:1、3—极限位置,选用一般位置(加粗实线)分析。

图4 轮履切换机构运动过程Fig.4 Movement Process of the Wheel-Track Switching Mechanism
在坐标系x′Ay′下,定义摆动杆杆长lAB、连杆长lBC、悬臂杆长lDC、底座销孔位置距离为lAD,构成的封闭矢量方程式(以复数形式表示)为:

式中:φ3、φ2、φ1—悬臂杆 3、连杆 2、摆动杆 1 与 x′轴的正方向的夹角;均以x′轴的正方向逆时针方向度量。
上式可解得φ3和φ1的关系:

同理,在坐标系xAy下得到θ1与伸缩杆长lEF的关系。其中:θ1为摆动杆与轴的正方向的夹角;θ2为电缸中轴线与轴的正方向的夹角;
又由关系 φ1=θ1-β,lEF=l0+δ,得到 φ1和 δ的关系。
式中:l0—电缸原长;
δ—电缸伸长量。
所以,最终可求得轮子最低点所在水平线与履带最低点所在水平线高度差:

式中:r—轮子半径;
R—履带轮半径;
lDH—悬臂杆3长度。
上极限位(轮式)时,h符号为正;h下极限位(履带式)时,符号为负。
通过h-φ3-φ1-θ1-lEF-δ,至此我们得到h与δ的位置间关系表达式。
将式(1)对时间求导数可得速度关系:

同理,得ω1表达式:

式中:v0—电缸推杆的运动速度。
由此我们得到机构ω3与v0的速度间关系。
上述分析对悬臂杆的驱动与控制相当重要,特别是在移动平台攀爬障碍时,悬臂杆需要定时定量且精准的完成起落,这需要对电缸推杆的伸长量进行严格控制,才能实现目的。
4 优化研究
4.1 定义变量
四杆机构设计是一个多变量、多目标、多约束、非线性的优化设计问题。
定义设计变量:

4.2 目标函数
为使在轮式模式下,机构实现自锁,避免电缸受震。要求摆动杆1竖直时,连杆2也竖直并与之重合,注意到此时状态的特点:φ2=3π/2-β。这里,将这一关系处理为φ2无限接近这个目标值,φ2可由式(1)解出。定义二者差值绝对值的最小值为目标函数。
在满足悬臂杆起落跨度需求下,我们希望角速度ω3变化范围越小越好。

根据此连杆机构的特性可知,ω3为递减函数,最大值出现在1位置,最小值出现在3位置。
还希望所需电缸推力(和拉力)越小越好。分析易见,机构在1位置,推杆受拉力最大;在履带刚脱离地面,轮子受到地面支撑(h=0)时推力最大。连杆为二力杆,摆动杆、悬臂杆均存在三力汇交。这里由于杆长参数未定,质量未知,且推力最大时速度较低,所以能用静力学分析代替动力学,忽略连杆重力与惯性力,提出的目标函数是必要不充分的,但是表明的关系、优化的方向是一致的。
分别对A、D点取矩,又得一目标函数:

式中:G—车体单元、履带模块和切换机构总重量,方向指向y轴负方向。
综上所述,轮履切换四杆机构优化设计的目标函数为:

式中:μ1、μ2、μ3—加权因子,和为 1。
4.3 约束条件
(2)履带模式下,终止位置电缸要与摆动杆呈一定角度不共线,设计传动角σ不小于[σ][10];
(3)运动过程中不能发生轮履之间、杆与杆之间的干涉等;满足以上条件,优化出各杆长及铰接孔位距离尺寸搭配。
建立数学模型:

由基本参数:标准台阶高×宽:(160×260)mm;故 160mm≤。电缸推力6000N,电缸初始长与行程关系:l0=δmax+105,选用δmax=100mm、l0=205mm。其它:r=127mm(8寸)、R=142mm、β=45°、G=1200N、v0=12mm/s。取:μ1=0.8、μ2=0.1、μ3=0.1。
4.4 优化结果
四杆机构优化问题是一个有限定条件的非线性规划问题。通过Matlab优化工具箱,将上述数学模型转换为程序语言,求解可得各参数值,如表1所示。(优化值取小数点后一位):

表1 轮履切换模块机构参数表Tab.1 Wheel-Track Switching Module Parameter Table
根据表中参数,编写程序,电缸伸长量δ在一定范围内按一定步长循环取值,对比优化前后h、ω3和Q的变化曲线,如图5所示。

图5 目标优化前后对比Fig.5 Comparison of Optimized Goals with Before
由图5看出,优化后的曲线,范围变小,坡度变缓,前者可提高效率、节省时间,后者使切换过程更平顺,速度和受力更合理。其中受力图中突变处为轮履切换的瞬间,受力情况由轮胎和履带的变形而定,并非突变,较为复杂,此处暂未作考虑。
5 结论
针对轮履复合移动平台的轮履切换机构进行了设计优化研究,获得了以下几点结果:(1)采用典型连杆机构,加入自锁特性,设计了一款轮履复合切换机构,解决了轮履复合及切换问题。(2)建立了连杆机构的运动学模型,从运动学的角度,分析了轮、履切换的运动过程,以及机构位置、速度、受力的状况,并求得输入与输出之间的运动关系。(3)提出了一种综合位置、速度、受力指标,对四连杆机构参数进行多目标优化的方法,获得了较优的四杆机构参数,为连杆机构的其他类似应用提供了参考。
