一种长悬臂梁结构动力学建模方法

赵宇飞，张中哲，李 科，王燕波，程远超

一种长悬臂梁结构动力学建模方法

赵宇飞，张中哲，李 科，王燕波，程远超

（北京精密机电控制设备研究所，北京，100076）

为了有效抑制长悬臂梁结构在受到固定端持续传来的周期性振动时在远端连接处产生的疲劳破坏，保护悬臂梁结构，需要对其远端连接处保持的辅助支撑机构施加一定的主动抑振控制算法。为此提出悬臂梁结构动力学建模，为控制算法分析、参数设计和研究提供模型基础。在对欧拉-伯努利梁振动模型和柔性基础简化模型的分析基础上，根据固定端输入的周期性振动信号推导出辅助支撑点处的含柔性基础悬臂梁振动微分方程，并结合梁的结构推导出符合实际的结构动力学模型。通过计算仿真，获得柔性基础悬臂梁的动态响应并确认了模型的准确性。因此为长悬臂梁结构提供了一种有效的建模方案并对具有柔性基础的机械臂的振动抑制具有一定的借鉴意义。

悬臂梁结构；柔性基础；结构动力学建模；振动抑制

0 引 言

近年发展起来的大型空间机械臂系统在航空航天领域做出了卓越的贡献。为了减少振动与定位误差，应用于传统工业的机械臂结构一般设计成高刚性结构，而在航空航天及精密机械领域，一类重量轻、能耗低、效率高、执行速度快且结构紧凑的柔性机械臂逐渐取代了传统高刚度结构，但抗弯刚度较低的机械臂将会在工作过程中不可避免地受到振动的影响[1]。这类振动问题一旦发生，仅仅依靠材料本身的阻尼很难自行衰减，会使系统损失定位精度、降低工作效率，严重时将会导致系统共振，大幅度缩短机械臂的寿命[2]。

在复杂的力学环境下，这类具有柔性基础的机械臂构型可以简化为多段连接而成的大型悬臂梁结构，由于结构存在柔性，受到梁的固定端传来的周期性振动时极易在远端连接处产生疲劳破环，使得这类大型悬臂梁结构产生惯性加速度过载而在远离固定端的连接处产生振动变形，甚至造成梁结构的共振。为延长结构的疲劳寿命，需要在远离悬臂梁固定端的末置位增加一个抱持机械臂，通过抑振控制算法实现悬臂梁结构前端交变载荷的减小。

本文将根据长悬臂梁结构的具体搭建方式与梁本身的实际结构进行模型抽象化，针对多段连接形成的外伸梁结构，采用简支梁和悬臂梁叠加的建模方式，分别进行结构动力学的建模，并根据两主挂点处输入的振动激励推导出传递至辅助支撑点处的振动激励，并通过仿真验证模型的准确性，为后期的抑振控制算法研究提供模型基础。

1 柔性基础悬臂梁振动模型建立

1.1 悬臂梁振动模型

悬臂梁在横向发生弯曲振动时，假定梁各个截面的中性轴都保持在同一平面内，作用于梁上的外载荷亦然，当梁结构收到固定端传来的振动时，弯曲变形成为梁的主要变形，当振动频率较低时一般忽略剪切变形以及截面绕梁的中性轴转动惯量的影响，这种梁模型称为欧拉-伯努利梁[3]。为了简化推导悬臂梁动力学模型，梁模型将采用欧拉-伯努利梁进行构建，悬臂梁弯曲变形示意如图1所示。

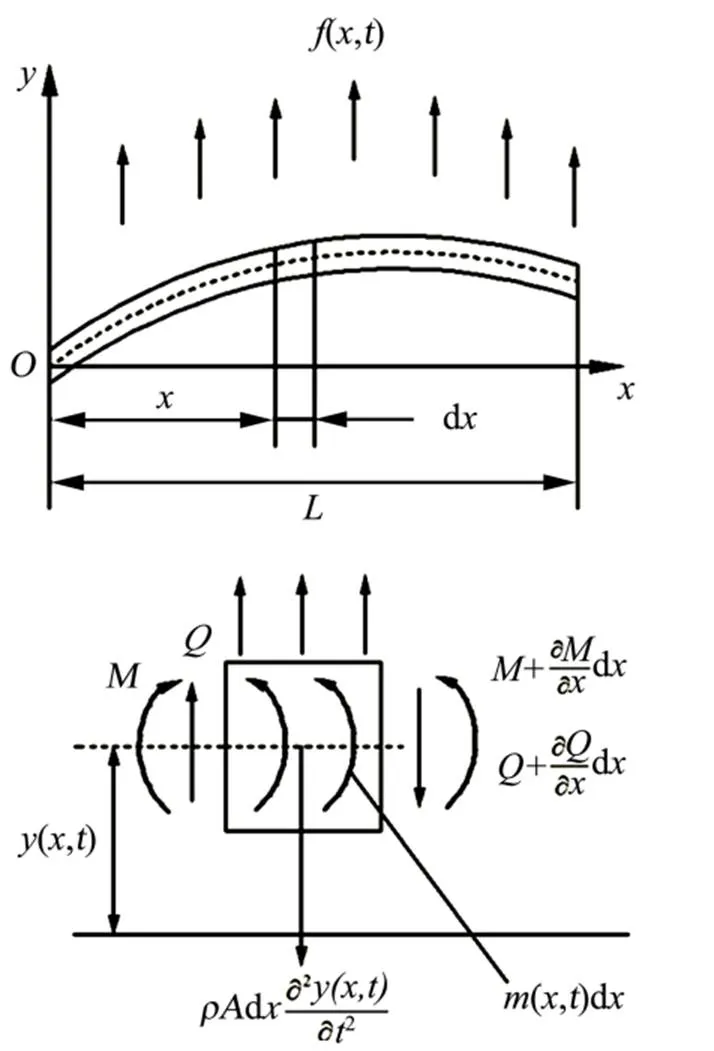
图1 悬臂梁弯曲变形示意

1.2 悬臂梁弯曲振动微分方程

取梁上任意微段d为研究对象，对其进行受力分析，根据力平衡方程得到：

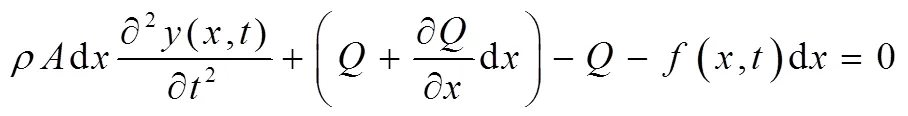
根据力矩平衡方程得：

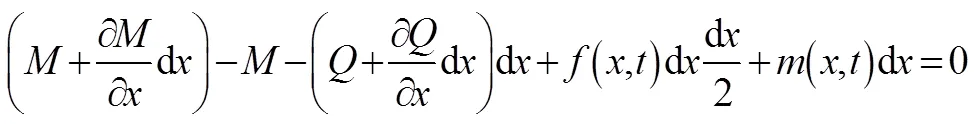
(d)2很小可忽略不计，式（2）可简化为

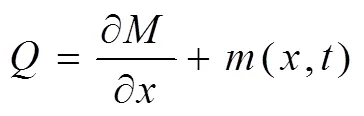
将式（3）代入简化后的力平衡方程，可得到：

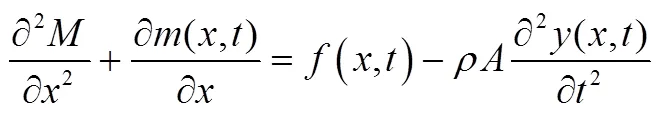
由材料力学的平截面假设[4]得知，梁所受弯矩与挠度之间存在如下关系：

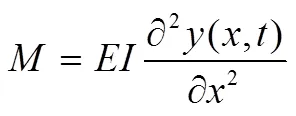
式中为材料的弹性模量；为梁截面对中性轴的惯性矩。

将式（5）代入简化后的平衡方程中可得：

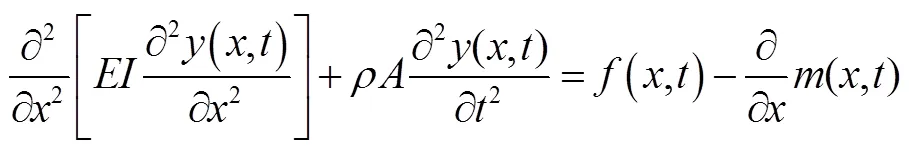
式（6）为根据欧拉-伯努利梁模型建立的悬臂梁弯曲振动微分方程。

1.3 悬臂梁的固有频率及振型函数

对于上述推导所得微分方程，如果所受外力()与外力矩()均为零，此时梁作自由振动，则此时的振动微分方程为

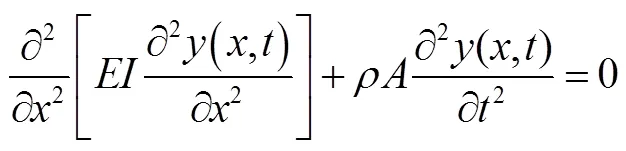
即：

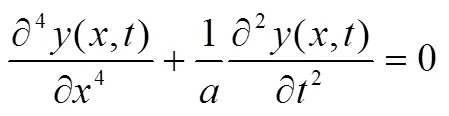
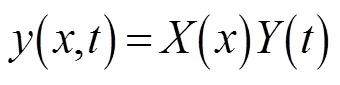
将式（9）代入简化后的式（8）中，得：

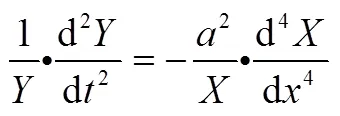
由式（10）可以看出，取左右两端等于同一常数2，则：

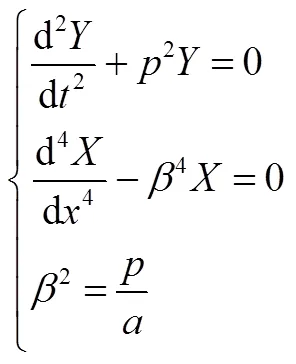
式（11）中第1个方程的通解为

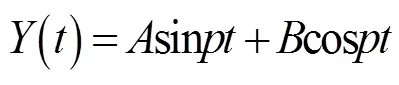
由于式（11）中第2个方程是一个4阶常系数齐次线性微分方程，其特征方程为

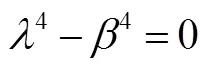
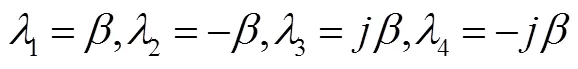
特征方程可简化为含待定参数c的下式：

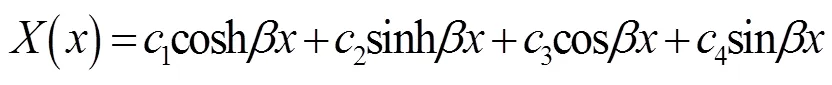
由此得到梁的主振动表达式为

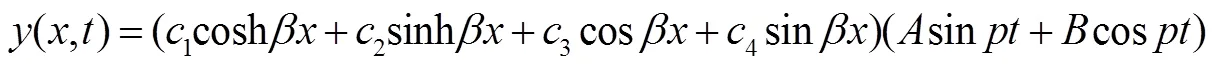
梁一端固定，另一端自由的边界条件[5]可以表示为

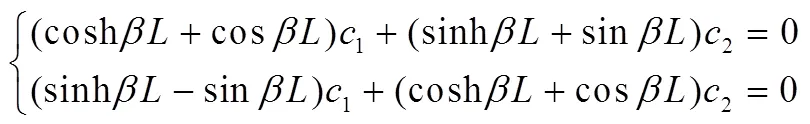
式（16）展开化简得到：

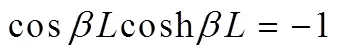
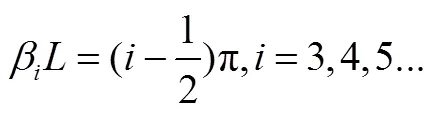
悬臂梁的各阶固有频率为

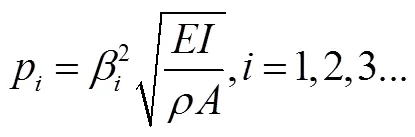
将各个特征值代入方程后可确定各个系数的比值，故对应的振型函数为

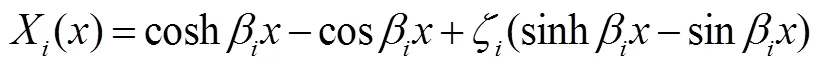
2 梁结构动力学建模

一个长约米，总重量为的长悬臂梁结构由主体和头端组成，结构主体和头端在点刚性连接，头端重M，质心在点处。结构整体通过相距L米的和两个主挂点以悬挂的方式吊挂运输，结构末端距离点为L米，以外伸梁的方式延伸到两个挂载点之外。

静止时，由于结构头端段没有辅助支撑，连接点和结构末端点较挂载点和延伸了较长的距离，在自然重力的重力下，延伸段的结构逐渐发生了弯曲形变，使得结构的点和点偏离理想水平轴线，使得结构表现出一定的柔性。同时在连接点处（头体连接处）受到了弯曲作用将会产生一定的弯矩载荷。当结构在自然重力下正常下垂时，末端距离理想水平轴线的距离为。

完成理论准备后回归结构建模，将长悬臂梁结构采用欧拉-伯努利梁进行建模，如图2所示。

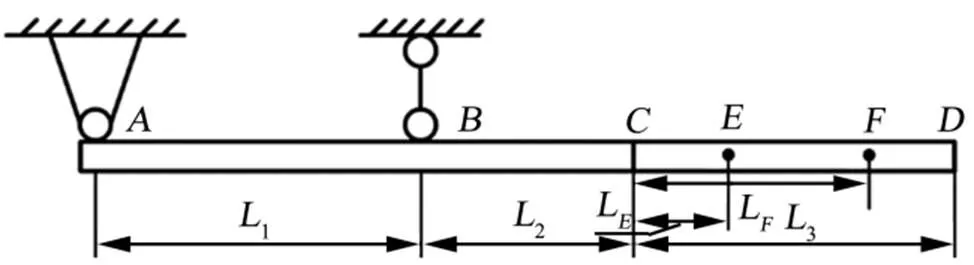
图2 结构的建模

1—两主挂点之间的距离；2—前挂点至产品头体连接处的距离；3—产品头体连接处至辅助支撑点的距离；L—产品头体连接处至头部质心的距离；L—产品头体连接处至辅助支撑点的距离

和分别为两个挂点，为结构头体连接处，为段的质心，为辅助支撑点。将外伸梁模型分解成和两段进行分析，并最后将结果进行叠加，最终得到结构的振动激励和动力学模型。其中，段可以等效为2个固定支点的简支梁，段可以等效为悬臂梁。

2.1 简支梁AB的建模

将段简化为简支梁进行建模，建模中为梁结构水平方向，为垂直轴线竖直向上方向，并将简支点作为坐标系原点，如图3所示。

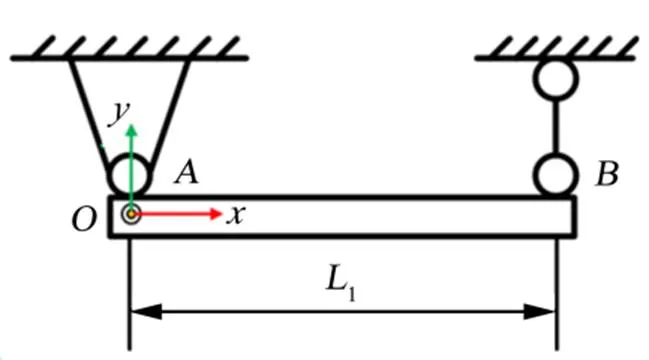
图3 简支梁模型

简支梁的结构动力学模型可以表示为

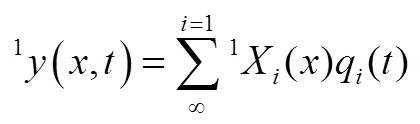
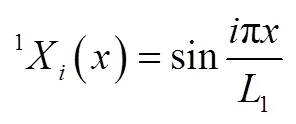
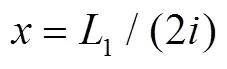
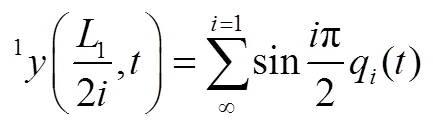
2.2 悬臂梁BD的建模

将段结构采用欧拉-伯努利梁进行建模，为梁结构水平方向，为垂直轴线竖直向上方向，并将固支点作为坐标系原点，如图4所示。

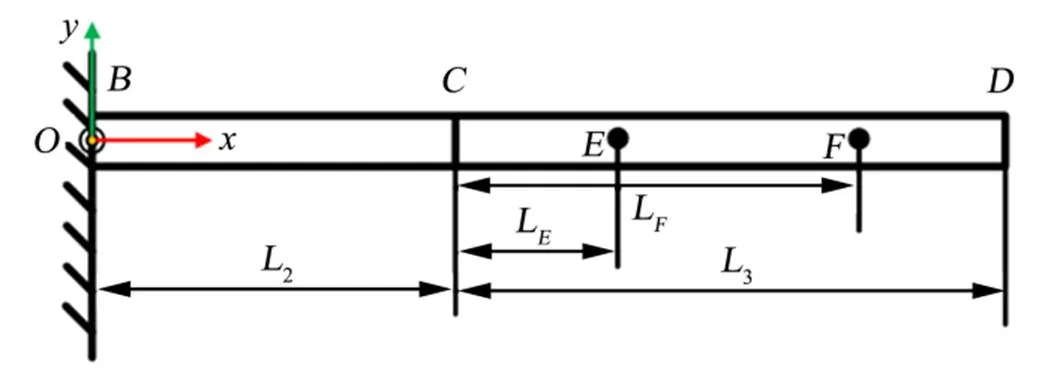
图4 悬臂梁模型

在悬挂段的点加入辅助支撑机构后，结构将被分解为两段：段和段。其中段较长可以使用悬臂梁模型进行等效；段较短，可以直接默认为刚体，并且由于段在辅助支撑点之后，且结构头端的质心在辅助支撑点之前，因此建模时可忽略段，只考虑段的悬臂梁建模。

对于无限多自由度的连续系统的动态响应，利用振型叠加法可以将其转化为无限个单自由度的模态相应的叠加，则段悬臂梁的微分动力学模型为

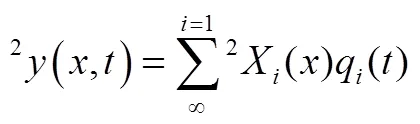
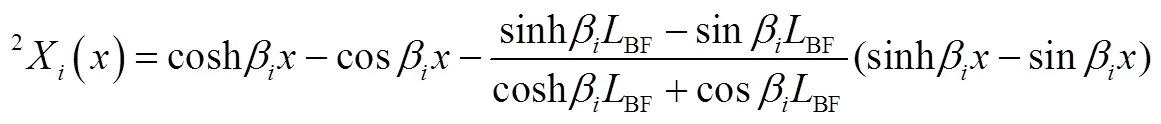
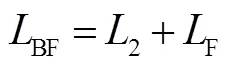
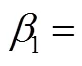
现在只考虑结构辅助支撑点的结构动力学，则点振型函数为

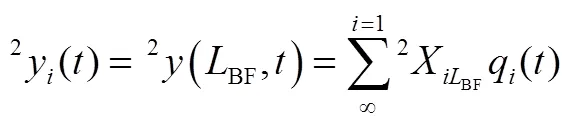
2.3 结构振型叠加

由上可得到由简支梁和悬臂梁振形叠加后的结构辅助支撑点的第阶模态的位移变形为

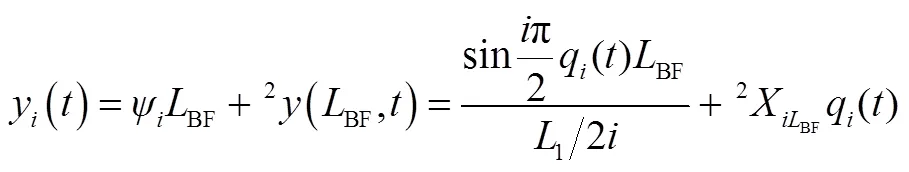
结构末端各阶模态振型导致的位移变形的总和为

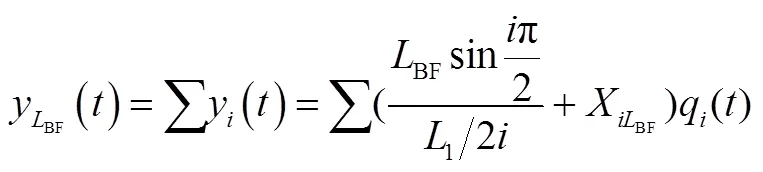
考虑简支梁变形微小，可将位移影响看作是一个简易杠杆，根据结构的尺寸数据可知，点的位移约为中点位移的2.81倍。为进一步确定振动输入对点带来的位移影响，在ANSYS中创建简支梁模型，并在两主挂点施加振动输入。在两主挂点施加振动输入后如图5所示。

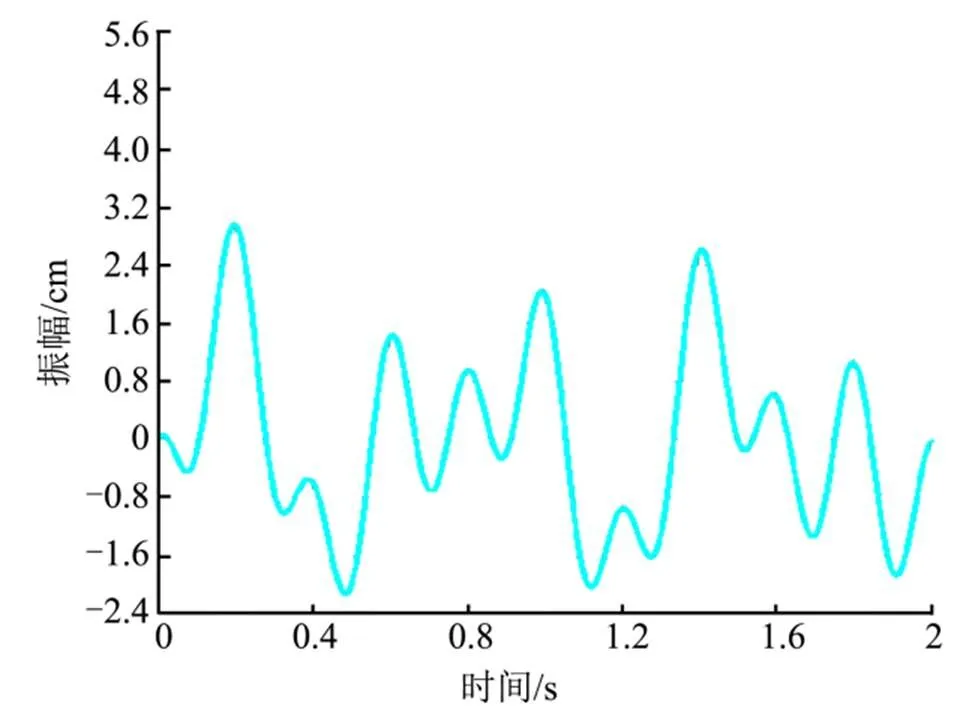
图5 时域波形

瞬态分析后得到中点的位移波形如图6所示。

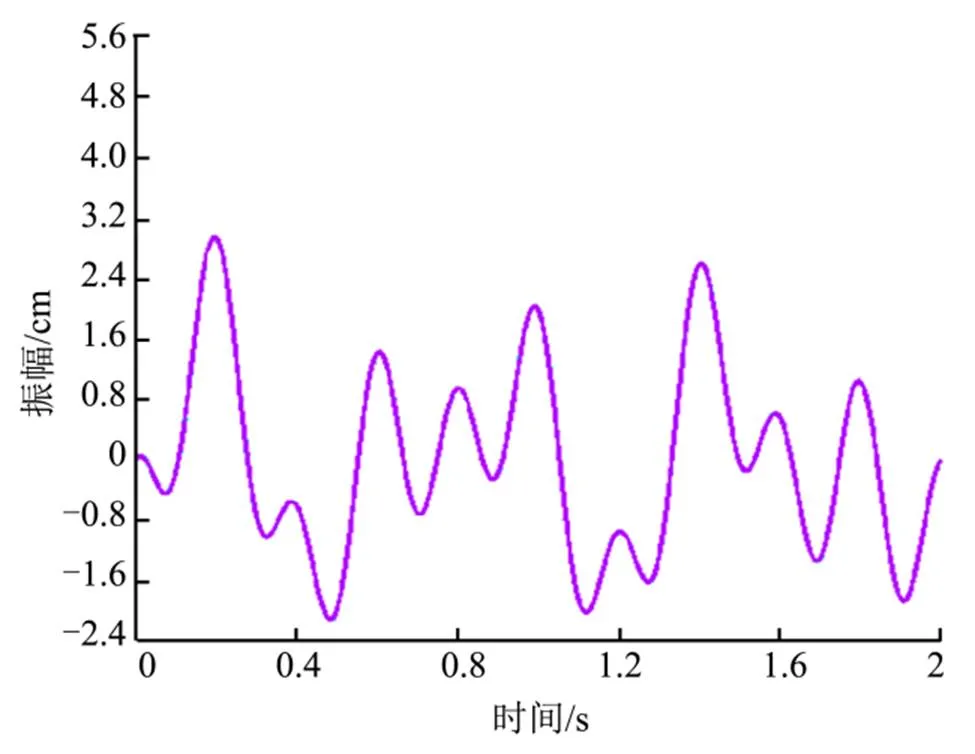
图6 位移波形

对比图5、图6可以看出，简支梁变形产生的挠角极其微小，因此在点产生的影响可以忽略不计，以下只对悬臂梁部分进行分析。

2.4 外力扰动下的结构动力学模型

考虑能量耗散时，长悬臂梁的结构动力学模型则可以化简得到广义坐标下的微分动力学方程：

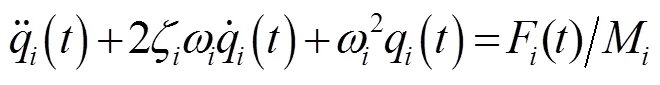
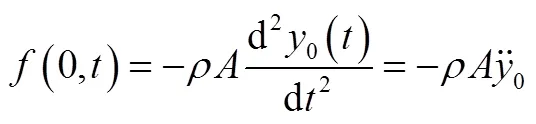
所以受到的广义力为

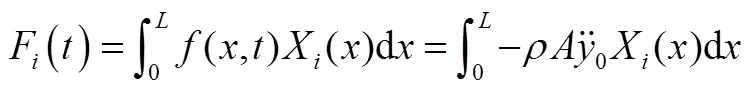
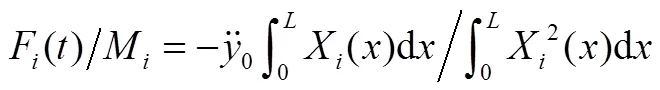
该振动将成为系统的激励，所以结构受迫振动时的微分方程为

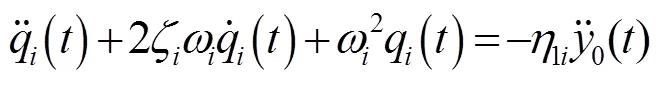
对式（33）进行拉普拉斯变换得到：

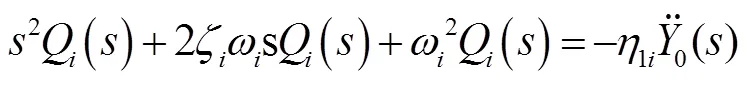
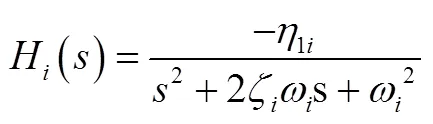
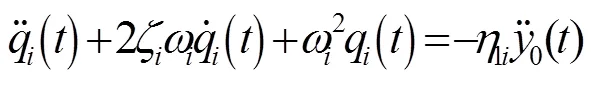
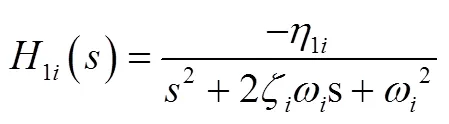
3 悬臂梁模型准确性验证

根据前面推导可知悬臂梁的第1、2阶振型函数为

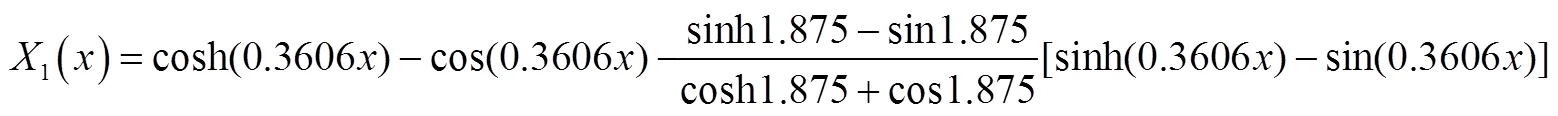
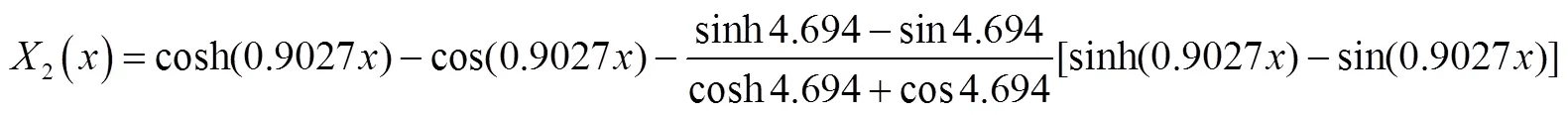
参考其他类似结构后初步假设结构的系统阻尼比=0.2，则有：

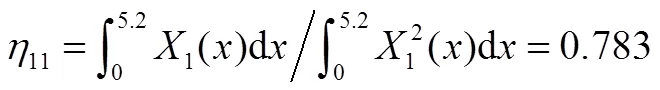
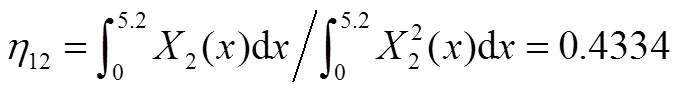
则可推出前两阶传递函数为

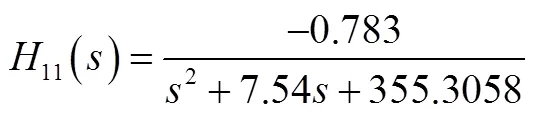
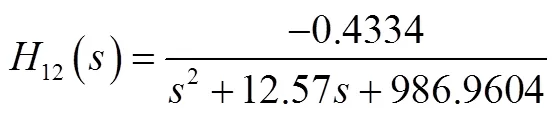
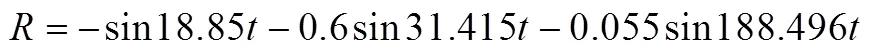
对比一阶和总输入相应可知，总位移输出主要由一阶响应构成，在之后的分析和控制中，将使用一阶的动力学模型作为主模型即可保证分析控制的准确性与实时性。

采用简化的只考虑一阶模态的动力学模型计算的点和点的位移比来和ANSYS中的全模态得到的两点的位移比进行对比验证，以验证理论模型的准确性和简化模型的有效性。

根据结构动力学和已知参数，将整个梁结构假设为只受到弯曲应力的悬臂梁，材料参数如表1所示。

表1 悬臂梁参数定义

Tab.1 Parameter Definition of Cantilever Beam

材料钢材 密度/(kg·m-3)7850 杨氏模量/GPa2.06 结构半径（等截面）/m0.2 泊松比0.31 阻尼系数0.2

点的微分动力学模型为

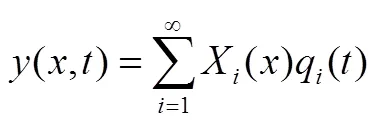
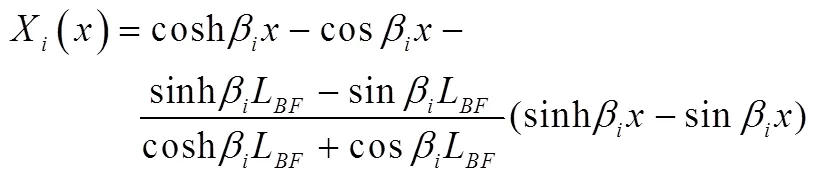
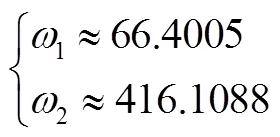
则辅助支撑点的振型函数为

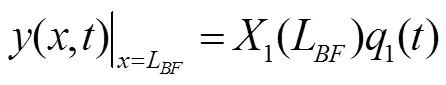
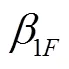
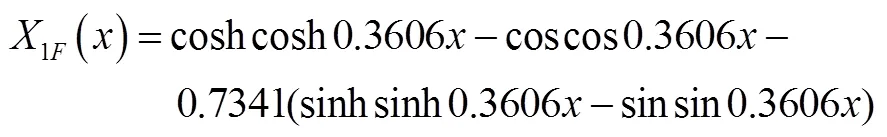
在外力扰动下，简化的结构动力学模型得：

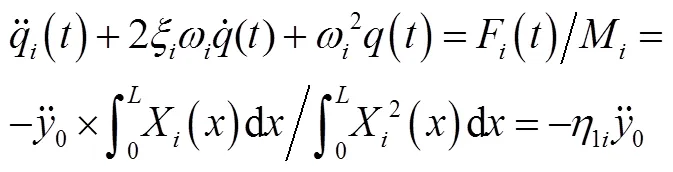
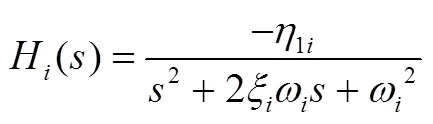
将点和结构参数代入得（仅考虑一阶）：

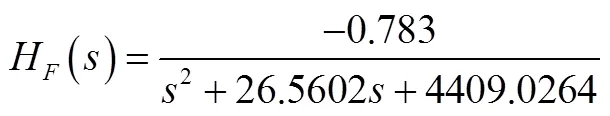
（52）

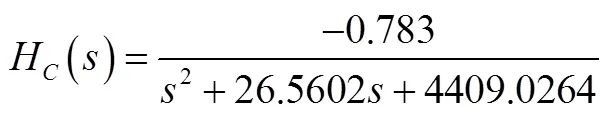
将L代入得到：

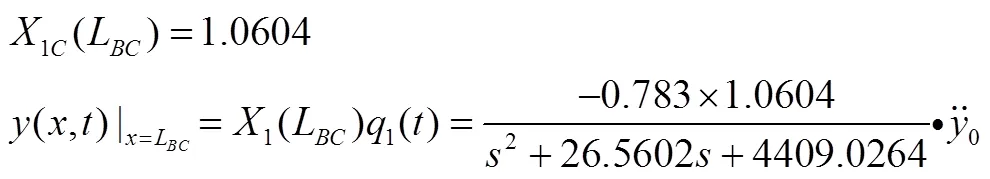
则，理论上点与点的一阶相对位移比为1.887。

进行模态分析得到悬臂梁的前两阶固有频率分别为10.571和65.209，可见固有频率与理论推导所得结果相符合。

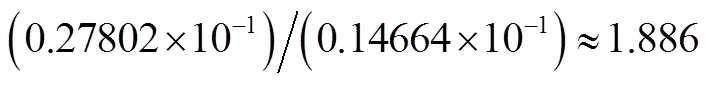
4 结 论

本文建立了一种多点支撑的长悬臂梁结构的动力学模型。首先介绍了欧拉-伯努利梁的概念，以其为理论基础分析了悬臂梁的振动特性，并建立了柔性基础悬臂梁的振动微分方程。然后根据悬臂梁的安装情况和实际结构进行结构动力学建模，并研究了该结构在外部振动激励情况下的动力学模型；随后推导出柔性基础模型的传递函数，结合悬臂梁振动模型推导出在外力扰动下的悬臂梁结构动力学模型，最后通过计算仿真，获得柔性基础悬臂梁的动态响应，并以此验证了所建立模型的准确性。

[1] 王达. 大型空间机械臂关节及其抑振控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.

Wang Da. Research on a large space manipulator joint and its vibration suppression control[D]. Harbin: Harbin Institute of Technology, 2012.

[2] 于登云, 孙京. 空间机械臂技术及发展建议[J]. 航天器工程, 2007, 16(4): 1-8.

Yu Dengyun, Sun Jing. Suggestion on development of chinese space manipulator technology[J]. Spacecraft Engineering, 2007,16(4): 1-8.

[3] 翟兆阳. 柔性基础悬臂梁振动主动控制[D]. 西安: 西安理工大学, 2010.

Zhai Zhaoyang. Active vibration control of a cantilever beam on elastic base[D]. Xi’an: Xi’an University of Technology, 2010.

[4] 白象忠. 材料力学[M]. 北京: 科学出版社, 2007.

Bai Xiangzhong. Mechanics of materials[M]. Beijing: Science Press, 2007.

[5] 郭闯强, 倪风雷，孙敬颋. 具有力矩传感器的柔性关节的振动抑制[J]. 机器人, 2011, 33(4): 449-454.

Guo Chuangqiang, Ni Fenglei, Sun Jingting. Vibration suppression for the flexible joint with torque sensor[J]. Robot, 2011, 33(4): 449-454.

[6] Virk G S, Al-Dmour A S. Real-time vibration suppression in a flexible cantilever rig[J]. Microprocessors and Microsystems, 2009(23): 365-384.

[7] 罗飞, 余达太. 主动式控制_机器人抑振控制的有效方式[J]. 机器人, 2015, 17(14): 23-27.

Luo Fei, Yu Datai. Active control_an effective method of reducing vibration control of robotics[J]. Robot, 2015, 17(14): 23-27.

[8] Xu W L, Han J D. Joint acceleration feedback control for robotics[J]. Robotic and Computer Integrated Manufacturing, 2000, 43(16): 207-320.

[9] 刘旭亮, 黄玉平. 柔性机械臂建模及动力学特性分析[J]. 噪声与振动控制, 2014, 34(6): 7-11 .

Liu Xuliang, Huang Yuping. Modeling and dynamic characteristic analysis of flexible robotic arm[J]. Noise and Vibration Control, 2014, 34(6): 7-11.

A Structural-Dynamic-Modeling Method for Long Cantilever Beam

Zhao Yu-fei, Zhang Zhong-zhe, Li Ke, Wang Yan-bo, Cheng Yuan-chao

(Beijing Research Institute of Precise Mechatronics and Controls, Beijing, 100076)

The long cantilever beam structure connected by multiple sections is often designed as a multi-point support. It is easy to generate fatigue and breakage at the distal joint when it is subjected to periodic vibration continuously transmitted from the fixed end, resulting in a significant reduction in fatigue life. In order to achieve effective vibration suppression and protect the structure, it is necessary to apply a certain active control algorithm to the auxiliary support manipulator holding the beam. The cantilever beam structure dynamics modeling proposed is intended for providing a model basis for parameter-designation of the control algorithm. Based on the analysis of the Euler-Bernoulli beam vibration model, the vibration differential equations of the beam are derived, and the actual structural dynamics model is established based on the structure of the beam. Finally, through the calculation and simulation, the dynamic response of the cantilever beam is obtained and the accuracy of the model is confirmed.It provides an effective modeling solution for the long cantilever beam structure and has certain reference significance for the vibration suppression of the manipulator with flexible foundation.

cantilever beam; flexible foundation; structure dynamic modeling; vibration suppression

TH113.1

A

1004-7182(2020)01-0083-06

10.7654/j.issn.1004-7182.20200115

2019-09-16；

2019-11-24

赵宇飞（1994-），男，硕士研究生，主要研究方向为航天机器人技术。

张中哲（1972-），男，研究员，主要研究方向为航天伺服控制。

李 科（1986-），男，高级工程师，主要研究方向为智能机器人与航天伺服控制。

王燕波（1978-），男，研究员，主要研究方向为空间智能机器人技术。

程远超（1990-），男，工程师，主要研究方向为机器人技术与应用。