采用有限元方法的平板锥形金属膜盒内压柱失稳研究

王亚军，陈牧野，周浩洋

采用有限元方法的平板锥形金属膜盒内压柱失稳研究

王亚军1,2，陈牧野2，周浩洋2

（1. 中国航天科技集团有限公司，北京，100084；2. 北京宇航系统工程研究所，北京，100076）

运载火箭蓄压器多使用平板锥形金属焊接膜盒，当膜盒充压超过其柱失稳临界压力时会发生柱失稳现象，为获得求解膜盒发生柱失稳压力的方法，使用有限元分析软件进行分析。首先利用ABAQUS非线性屈曲法求解膜盒柱失稳临界压力值，然后利用有限元方法求解膜盒在不同压力下的拉伸、压缩刚度值，结合推导的膜盒柱失稳理论计算式，得到了一种平板锥形金属膜盒内压柱失稳临界压力值计算方法，将计算结果与试验结果进行对比，验证了方法的适用性。

平板锥形；柱失稳；非线性；有限元方法；刚度

0 引 言

大型液体火箭已有的飞行试验显示，火箭的结构与推进系统之间存在相互作用，使液体火箭产生闭合回路的不稳定性纵向振动，即“POGO”振动[1]。抑制POGO振动最简便的方法就是在推进剂输送管路上设置抑制装置蓄压器。目前，中国的运载火箭采用安装金属膜盒式蓄压器来抑制“POGO”振动。而膜盒式蓄压器的核心部件平板锥形金属膜盒在内压过高时会发生柱失稳，导致蓄压器失效，因此掌握平板锥形金属膜盒的柱失稳规律变得十分重要。

膜盒柱失稳规律研究可以采用理论方法[2,3]和有限元方法。随着计算机技术的发展，有限元方法在工程问题中得到广泛的应用。近年来非线性有限元发展迅速，使得求解非线性屈曲问题的方法越来越完善，更多的学者选择使用有限元方法来求解屈曲问题。

针对平板锥形焊接金属膜盒的刚度和强度问题，有学者已经采用有限元方法进行了相关研究。史淑娟[4]等针对充气膜盒在充气气压作用下相邻膜片出现贴合的状态，分析了考虑接触非线性对刚度的影响，最后借助ANSYS软件的接触分析求得了充气膜盒在出现接触状态下的刚度。娄路亮[5]采用有限元分析软件对不同结构的焊接波纹管进行强度、刚度和模态分析。

针对膜盒类产品的稳定性问题，有限元方法已经被广泛地运用于U型、碟形波纹管的稳定性研究。张庆[6]等采用ANSYS软件，用有限元法对同时承受轴向、横向和转角位移载荷的U型波纹管进行内压稳定性分析。刘岩[7]等针对碟形金属波纹管，使用ANSYS非线性稳定性分析，通过与试验值相比对，证明了有限元模型能够较好地分析碟形波纹管的稳定性。李杰[8]等针对多层波纹管，考虑了其在内压载荷下的层间接触问题和稳定性屈曲问题，对非线性屈曲初始缺陷的施加进行了描述，最终在载荷位移曲线上，采用双切线交点法得到失稳临界载荷。

本文首先采用非线性有限元屈曲分析方法，再采用柱失稳理论公式和有限元计算刚度相结合的方法，分别对平板锥形金属膜盒的内压柱失稳临界压力进行求解，并将不同方法的计算结果与试验结果进行比较，为后续相关研究提供借鉴。

1 膜盒内压柱失稳有限元仿真分析

针对不同目的和屈曲特点，应用有限元分析软件ABAQUS可有如下屈曲分析方法[9]：弧长法分析，隐式动力分析，显式动力分析，线性屈曲分析，通用静力分析。

目前的研究中，多使用弧长分析法求解屈曲临界压力，因为弧长法可以求解后屈曲过程，但该方法求解后屈曲过程时，要求平衡路径必须是连续的，当存在接触分离的情况时，平衡路径就会出现不连续现象，因此结构中若存在接触时，使用弧长分析法极容易出现求解不收敛问题。而膜盒在充压状态下接触分离现象不可避免，因此仿真膜盒柱失稳不适合采用该方法求解。隐式动力分析和显式动力分析法同样不适用于仿真膜盒失稳，因为膜盒结构较复杂，分析过程涉及几何非线性、物理非线性和接触非线性，计算费用高昂且耗时过长。线性屈曲法只考虑弹性变形，而未考虑膜盒非线性变形，故所求得的失稳临界压力值为发生失稳的上限压力值，与实际失稳值相差较大。通用静力分析法考虑了非线性因素，在引入线性屈曲模态后，虽不能准确求解后屈曲状态，但可以用来判断进入失稳的临界压力值。综上分析，本文使用通用静力分析法求解膜盒的柱失稳临界压力值。

本文的研究对象均为平板锥形金属膜盒，其膜片结构示意和膜盒示意如图1所示。

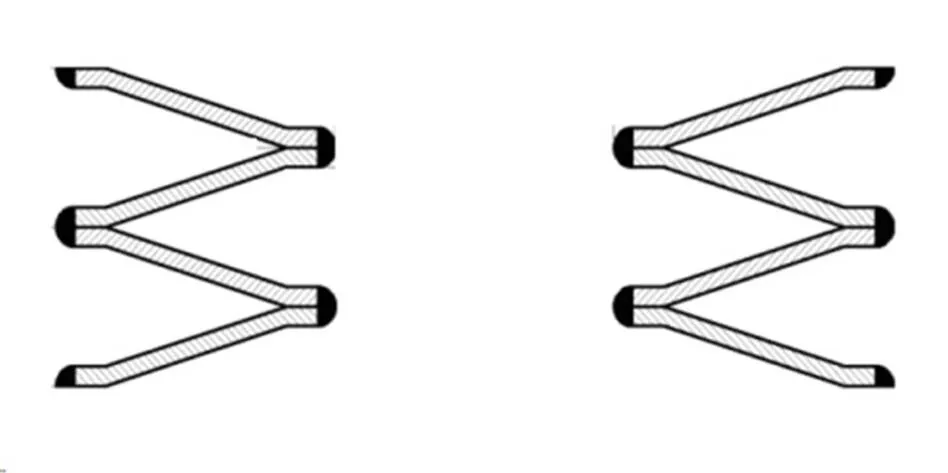
a）膜片结构

b）金属膜盒

续图1

本文中可能使用到的膜盒的具体尺寸参数以及柱失稳试验值如表1所示，各膜盒的材料参数如表2所示。

表1 各膜盒尺寸参数及柱失稳试验值

Tab.1 Size Parameters and Column Instability Experiment Values

膜盒代号外径mm内径mm直边长mm膜片厚度mm膜片高度mm膜片数片柱失稳试验值MPa 11401041.50.21.5500.4 2523210.21600.75 3816610.120.4960.4 41701461.50.21561.4 52001701.50.31.33600.9 61401041.50.21.5480.3 717014610.20.861000.32

表2 各膜盒材料参数

Tab.2 Material Parameters

膜盒代号弹性模量GPa屈服强度MPa抗拉强度MPa断面延伸率泊松比 120013001500200.3 220013001500200.3 320013001500200.3 420013001500200.3 5200520850300.3 62006501000200.3 7200520850300.3

整个膜盒属于薄壳结构，因此膜盒采用壳模型进行建模。整个膜盒的有限元模型和网格划分如图2所示，采用S4R四节点壳单元进行网格划分，对于靠近内缘处的膜片斜边段以及焊缝处的网格进行了加密。

图2 膜盒有限元模型和膜片网格划分

在文献[2]中已经推导了考虑拉伸、压缩刚度不一致的平板锥形焊接金属膜盒内压柱失稳计算公式，文献中指出对于不满足刚度不变基本假设的膜盒，公式计算的结果误差较大。因此本文选择使用有限元方法，以期能够获得这一类膜盒较为准确的失稳内压值。

屈曲可以定义为结构处于一种状态，当载荷增量为一个微量时，其位移增量很大。逐级施加载荷，得到载荷-位移曲线，当载荷增量较小，而位移增量较大时，即认为发生失稳，在载荷-位移曲线中通过双切线法可以获得失稳临界压力值。

在使用通用静力分析法进行非线性屈曲分析前，需要使用线性屈曲分析获得膜盒的失稳模态。采用的边界条件为上、下两个端面固支。施加单位内压载荷，求解膜盒的一阶和二阶失稳模态及其对应的失稳压力。

以1号膜盒作为研究对象，其一阶、二阶线性屈曲失稳模态及失稳压力结果见表3。

表3 1号膜盒线性屈曲分析结果

Tab.3 Linear Buckling Result of Bellows 1

模态阶数失稳模态失稳值/MPa 一阶0.327 二阶0.646

使用通用静力分析法分析膜盒的柱失稳，采用的边界条件为上、下两个端面固支。使用*imperfection语句将线性屈曲分析获得的一阶模态按照一定比例引入作为非线性屈曲分析的初始缺陷。施加线性屈曲分析获得的一阶失稳值两倍大小的内压载荷，当内压载荷达到线性屈曲一阶特征值的两倍或因结构变形过大导致不收敛时计算终止。

仍以1号膜盒作为研究对象，分别将一阶屈曲模态的0.1%、0.3%和1%引入金属膜盒有限元模型作为非线性分析的初始缺陷，计算由于结构变形过大导致不收敛而终止。绘制位移最大节点的载荷-位移曲线，如图3所示。由图3可知，引入不同比例缺陷的3条曲线均在0.22 MPa和0.42 MPa处产生明显拐点，符合载荷增量较小而位移增量较大的条件。因3条曲线的拐点一致，故对引入0.3%一阶屈曲模态的结果展开进一步分析。

图3 1号膜盒位移最大节点的载荷-位移曲线

通过观察膜盒在拐点后一定压力范围内的变形形态来确定膜盒具体的柱失稳临界压力值，提取拐点后0.23 MPa和0.43 MPa下的变形云图，进行适当放大后如图4所示。

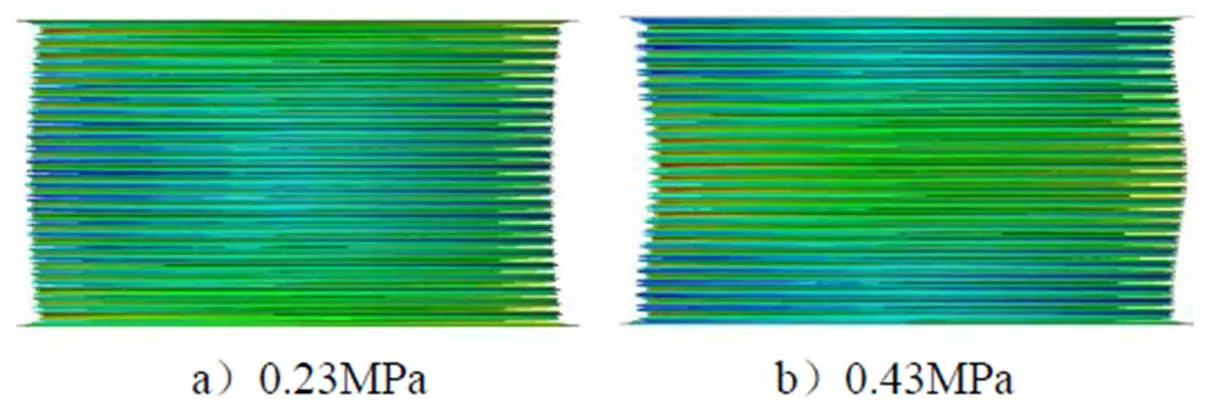
图4 膜盒变形

从图4中可以观察到在0.23 MPa下，膜盒的中心轴线整体发生了侧移，呈现出一阶失稳模态且与试验柱失稳模态一致。在0.43 MPa下，膜盒呈现出二阶失稳模态，与实际试验结果不符，因此认为0.22 MPa为膜盒的柱失稳临界压力。

以其它膜盒为研究对象，使用线性屈曲分析获得一阶屈曲模态，再将一阶屈曲模态的0.3%引入模型作为初始缺陷进行仿真，获取其载荷-位移曲线（如图5所示）。若曲线中出现多个拐点，则观察不同拐点压力后膜盒的变形形态，选择变形形态与试验一阶柱失稳形态一致的为柱失稳临界压力值，失稳值汇总结果如表4所示。

图5 各膜盒的节点位移-载荷曲线

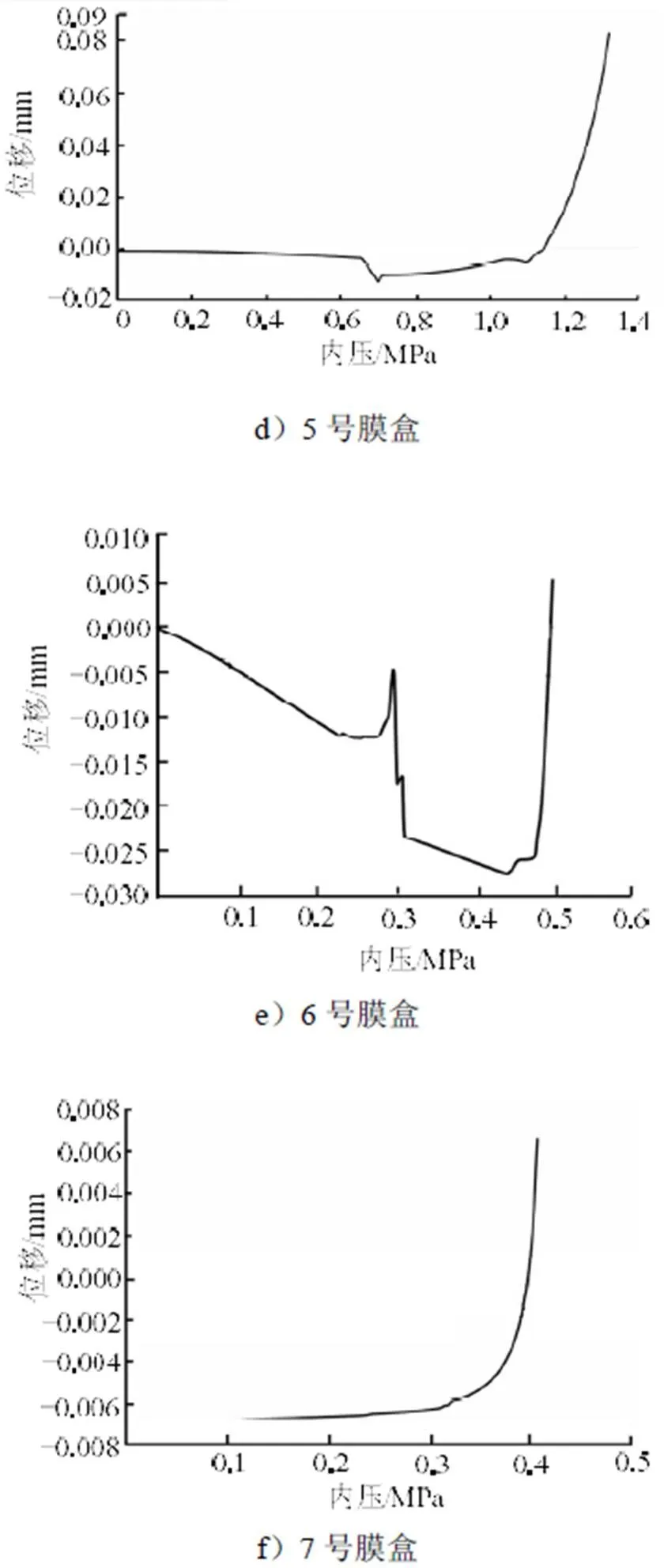
续图5

表4 采用通用静力分析获得的各膜盒失稳值

Tab.4 The Column Buckling Pressure Using Non-linear Buckling Method

膜盒代号失稳试验值MPa非线性屈曲分析得到的失稳值MPa误差 10.40.22-45% 20.750.7-6.7% 30.40.6665% 41.40.67-52.1% 50.90.68-24.4% 60.30.28-6.7% 70.320.4128.1%

由表4中可见，采用引入线性屈曲模态的通用静力分析法可以分析膜盒的柱失稳临界压力，但与试验结果相比，有的膜盒计算结果偏差较大，达到了-52.1%和65%。

2 结合柱失稳理论公式的有限元仿真分析

由于直接使用通用静力分析法求解时部分膜盒的柱失稳临界压力结果误差偏大，因此考虑将有限元方法和理论公式进行结合求解膜盒的柱失稳临界压力值。

在文献[2]中，通过对膜盒建立理论模型求解，已经获得了膜盒的柱失稳临界压力理论公式[3]：

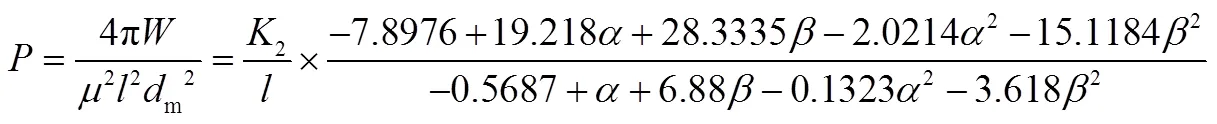
平板锥形膜盒在内压的作用下，膜片之间产生的接触以及一些其它原因会导致膜盒的机械刚度随内压发生变化，在这种情况下，式（2）可能不能准确表达膜盒的刚度。其中，5号膜盒在文献[2]中就已被证明使用式（2）计算后获得的失稳内压值误差过大。

因此考虑使用有限元软件获取不同膜盒在不同内压值下的拉伸、压缩机械刚度，再将有限元求得的这些刚度值代入到公式中求解柱失稳临界压力。

2.1 充内压下的膜盒机械刚度有限元仿真

建立膜盒的轴对称模型，采用CAX4I非协调四节点双线性轴对称单元。求解膜盒的轴向机械刚度时，给膜盒的内表面施加一定的内压载荷，将底端面固支，顶面施加轴向位移载荷。提取出该内压下不同轴向位移对应的顶面轴向支反力，通过支反力和位移的关系求出在该压力下膜盒的轴向机械刚度。

各膜盒在不同内压下的拉伸、压缩机械刚度值如图6所示。

图6 各膜盒在不同内压下的拉伸、压缩刚度曲线

由图6可见，5号膜盒的刚度在不同内压下有着较大的波动，因此无法直接使用式（2）计算5号膜盒的刚度。除了5号膜盒，其余膜盒在不同内压下的刚度也存在一定的变化。可见充压确实导致膜盒的刚度产生了变化，因此直接在公式中使用不充压的机械刚度是不准确的。观察图6曲线还可以发现，大部分膜盒刚度会存在一个较剧烈的升高，这是由于膜盒的中部膜片在该压力值附近发生了贴合，引起膜盒整体刚度的变大。

由图6中各曲线走势可以发现，不同膜盒的刚度-内压曲线变化规律不一致，使用统一的公式表达来描述充内压下的刚度值较为困难，因此采用有限元方法求解不同内压下膜盒的拉伸、压缩刚度值。

2.2 考虑充压下机械刚度的膜盒柱失稳分析

由式（1）知，膜盒的抗弯刚度可以由膜盒的拉伸、压缩机械刚度求得，是膜盒抵抗柱失稳的一个重要因素。在其他条件相同的情况下，每一个抗弯刚度确定了结构在该抗弯刚度下不发生柱失稳可以承受的最大压力值，即膜盒的柱失稳临界压力值。给定一个膜盒内压，采用轴对称模型可以求出压力下膜盒的拉伸、压缩机械刚度，进而求得该内压下膜盒的抗弯刚度，采用此抗弯刚度可以求出此时膜盒的失稳临界压力，若给定的膜盒内压大于失稳临界压力表明膜盒在该内压下会发生失稳。

以抗弯刚度为横坐标，由抗弯刚度求出的临界失稳压力为纵坐标，如图7所示，可以得到不同抗弯刚度下膜盒的失稳压力线，位于该线上方的部分表示结构处于失稳状态。

图7 抗弯刚度-压力曲线与失稳区域

以实际压力为纵坐标，该压力下的膜盒抗弯刚度为横坐标，即可以得到膜盒在不同内压下的膜盒抗弯刚度曲线。将该曲线与不同抗弯刚度下膜盒的失稳压力线绘制在一起。两线的第1个交点对应的压力值即为膜盒发生失稳的临界压力值。

由于公式理论模型与实际膜盒之间存在偏差，实际失稳值可能与理论公式值有一定误差。若图中的曲线存在未相交但相距较近的情况，以5%作为理论计算值与实际值之间可允许的误差，考虑理论值5%误差后获得的交点压力值仍可视作膜盒的柱失稳临界压力值。

各膜盒失稳曲线如图8所示，失稳结果见表5。

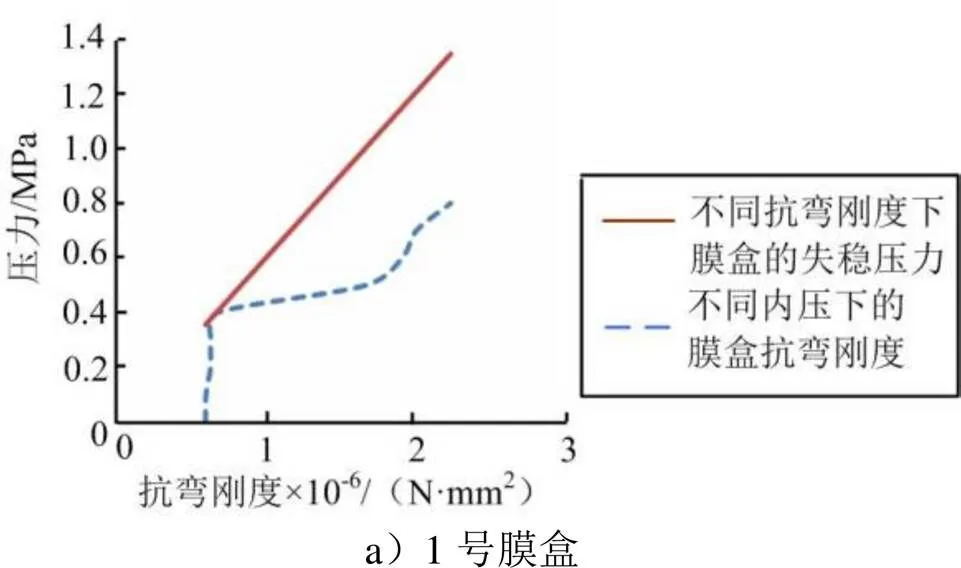
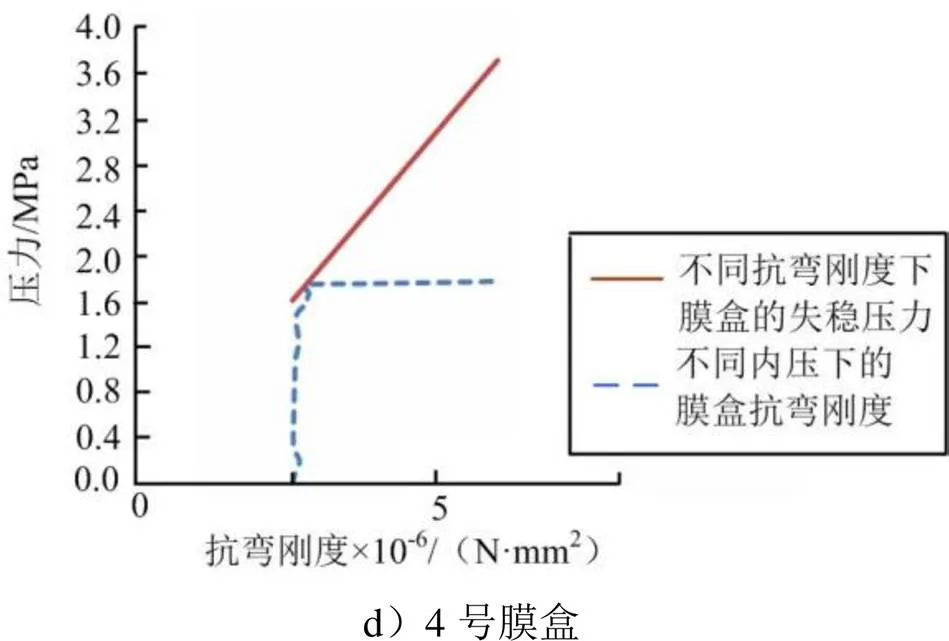
图8 各膜盒失稳曲线

续图8

表5 各膜盒失稳值汇总

Tab.5 The Column Buckling Result of Different Method 膜盒试验值MPa失稳值/MPa误差 方法一方法二方法三方法一方法二方法三 10.40.220.3950.28-45%-1.25%-30% 20.750.70.770.73-6.7%2.7%-2.67% 30.40.660.530.565%32.5%25% 41.40.671.71.36-52.1%21.4%-2.86% 50.90.681.181.74-24.4%31%93.3% 60.30.280.3650.29-6.7%21.6%-3.3% 70.320.410.3250.4628.1%1.6%43.75%

注：方法一为使用通用静力分析法计算得到的失稳值；方法二为使用有限元计算刚度得到的失稳值；方法三为使用理论公式计算刚度得到的失稳值，其中5号、7号膜盒不满足文献[2]中提出的充压刚度基本不变条件

表5中柱失稳计算分析结果与膜盒试验结果之间存在一定偏差，这些偏差主要是由以下原因所致：

a）膜片的实际几何形状（如壁厚、内外径等尺寸）与理论存在偏差；

b）柱失稳试验采用目视估读的方法获取失稳值，该方法存在一定的随机误差。

由表5可知：对比方法一和方法二，方法二结果误差范围明显优于方法一；对比方法二与方法三，这2种算法都是基于式（1）求解膜盒柱失稳压力，均可以用于求解膜盒的内压柱失稳临界压力。在文献[2]中指出，使用方法三膜盒需要满足充压情况下轴向刚度保持基本不变的条件，故方法三适用范围较小。方法二可以分析充压后的膜盒刚度，扩大了式（1）的适用范围。此外，方法二的误差范围为-1.25%～32.5%，方法三在适用范围内（排除5、7号膜盒）的误差范围为-30%～25%，方法二的离散度更小。

广播电视节目的传统传播机制，也就是立足于传统媒介的广播电视。在广播电视台普遍邀请受众现场参与节目录制，以及互联网以家用计算机和智能手机为终端进入百姓生活之前，信息的发布与接收是单向的。如果受众希望与节目制播机构交换信息，则必须借助纸质媒介或有线电话，这时候的双向交流具有滞后性。此时，信息的传播机制可以用图1表示。

3 结束语

本文使用ABAQUS软件，按比例引入线性屈曲模态作为初始缺陷，利用非线性通用静力分析法分析膜盒的柱失稳，通过求解载荷-位移曲线拐点获得膜盒失稳值。结果显示该方法可以用来求解膜盒的柱失稳问题，但部分结果与实验结果相比偏差较大。且使用有限元仿真分析获取膜盒在不同内压下的拉伸、压缩刚度值，结合理论公式，通过求解曲线交点的方法，求得膜盒的内压柱失稳值，扩大了式（1）的使用范围。

金融市场的核心环节就是金融资产的定价，倘若金融资产定价机制模糊，自然就会造成整个金融市场的混乱。同样互联网金融市场也逃离不了。而且由于互联网金融作为新兴产业，其定价机制并没有像传统金融产业那样十分清晰的定价标准，更多的都是处于摸索当中。而且由于互联网金融风险根本无法计量识别，在资产定价时也无法将相关风险因素纳入到考虑范围中，因此对于互联网金融市场的发展来说是极为不利的。当下互联网金融产品的价格更多的是依赖市场供需关系所决定的，但是这就会脱离实际，不利于金融产品价值的评估，而且十分容易因为市场的不稳定从而引发金融资产的价值的不稳定。

参 考 文 献

[1] 廖少英. 液体火箭推进增压输送系统[M]. 北京: 国防工业出版社, 2007.

Liao Shaoying. Liquid rocket propellant and pressurization feed systems[M]. Beijing: National Defense Industry Press, 2007.

[2] 王亚军, 等. 平板锥形金属膜盒内压柱失稳理论研究[J]. 导弹与航天运载技术, 2019(6): 11-16.

Wang Yajun, et al. Reserch on column buckling calculation formula under internal pressure of plane-cone shaped bellows[J]. Missiles and Space Vehicles, 2019(6): 11-16.

[3] 朱卫平. 波纹管在内压作用下柱失稳临界压力的计算[J]. 力学与实践, 2002(5): 32-35.

Zhu Weiping. Instability analysis of corrugated cylinder under internal pressure[J]. Mechanics in Engineering, 2002(5): 32-35.

[4] 史淑娟, 等. 考虑接触的膜盒刚度分析[J]. 导弹与航天运载技术, 2003(2): 41-44.

Shi Shujuan, et al. Non-linear stiffness analysis for metal bellows[J]. Missiles and Space Vehicles, 2003(2): 41-44.

[5] 娄路亮, 等. 焊接波纹管的非线性力学分析与试验研究[C]. 黄山: 全国膨胀节学术会议, 2006.

Lou Luliang, et al. Nonlinear mechanical analysis and experimental study of welded bellows[C]. Huangshan: China Pressure Vessel Institute Expansion Section Committee, 2006.

[6] 张庆, 等. U型波纹管稳定性非线性有限元分析[J]. 南京理工大学学报(自然科学版), 2002, 26(3): 270-273.

Zhang Qing, et al. Nonlinear finite element analysis of stability of u-shape bellows[J]. Journal of Nanjing University of Science and Technology, 2002, 26(3): 270-273.

[7] 刘岩, 等. 碟形金属波纹管的内压稳定性研究[J]. 压力容器, 2007, 24(4): 4-9.

Liu Yan, et al. Research on instability of v-shaped metal bellows under internal pressure[J]. Pressure Vessel Technology, 2007, 24(4): 4-9.

[8] 李杰, 段玫. 多层波纹管接触分析及稳定性屈曲分析[J]. 材料开发与应用, 2011, 26(6): 53-57.

Li Jie, Duan Mei. Analysis on contact and stable squirm of multi-ply bellows[J]. Development and Application of Materials, 2011, 26(6): 53-57.

[9] 江丙云, 孔祥宏, 罗元元. ABAQUS工程实例详解[M]. 北京: 人民邮电出版社, 2014.

Jiang Bingyun, Kong Xianghong, Luo Yuanyuan. ABAQUS detailed engineering examples[M]. Beijing: The People's Posts and Telecommunications Press, 2014.

Research on Column Buckling Calculation Formula under Internal Pressure of Plane-cone Shaped Bellows Using Finite Element Method

Wang Ya-jun1,2, Chen Mu-ye2, Zhou Hao-yang2

(1. China Aerospace Science and Technology Corporation, Beijing, 100084; 2. Beijing Institute of Astronautical System Engineering, Beijing, 100076)

Abstract: Rocket accumulator uses plane-cone to shape metal bellows, these bellows will occur column instability under internal pressure. To obtain the method of calculating the buckling pressure of metal bellows, firstly, nonlinear method using ABAQUS is used. Secondly, the finite element method is used to calculate the tensile and compressive stiffness values of the bellows under internal pressure. Combining with the deduced theoretical formula for calculating column pressure value of plane-cone shaped bellows and experiment results, an engineering acceptable calculation method for critical column pressure of plane-cone shaped bellows under internal pressure is obtained.The calculation results are compared with the experiment results to be proved valid.

Key words: plane-cone shaped; column buckling; nonlinear; finite element method; stiffness

中图分类号：V42

文献标识码：A

文章编号：1004-7182(2020)01-0007-07

DOI：10.7654/j.issn.1004-7182.20200102

收稿日期：2018-01-06；

修回日期：2018-04-12

作 者 简 介

王亚军（1966-），男，博士，研究员，主要研究方向为飞行器设计。

陈牧野（1992-），男，工程师，主要研究方向为增压输送系统设计。

周浩洋（1974-），男，博士，研究员，主要研究方向为增压输送系统设计及仿真研究。