一种基于三框架四轴惯性平台的飞转判断算法

张 娜，赵军虎，余贞宇

一种基于三框架四轴惯性平台的飞转判断算法

张 娜，赵军虎，余贞宇

（北京航天控制仪器研究所，北京，100039）

针对三框架四轴平台系统的飞转判断算法进行了研究，详细分析了平台系统产生飞转的基本原理，并根据三框架四轴平台特点设计了基于软件实现的飞转判断算法。当惯性平台系统出现框架超速时，通过该方法可以实现飞转的快速判断，同时还能有效降低飞转判断的虚警率，有效预防由于平台飞转造成的巨大损失，对于提高平台的可靠性有重要意义。

惯性平台系统；三框架四轴；飞转判断

0 引 言

惯性平台是导弹、运载火箭等飞行器中制导与控制系统中的核心部件，主要是为相关飞行器建立惯性空间的方位和姿态角基准，包括陀螺仪、加速度计和伺服回路。陀螺仪测量飞行器相对惯性空间的角度、角速度，加速度计测量飞行器相对惯性空间的速度和加速度。陀螺仪、加速度计能否正常工作直接关系着飞行器的可靠性。

惯性平台失稳倒台是惯性平台测试和正常工作中应重点防范的故障。当外部环境过载或稳定回路的某一环节发生故障时，可能导致系统不稳定发散或开环，引起环架伺服电机单向驱动，造成平台环架从原来的稳定位置向某一边快速转动倒下，由于惯性平台上环架和陀螺具有交耦性，在高速率的情况下，会引发其它各环架伺服回路的同时倒环，这就是所谓的惯性平台失稳倒台。如果不及时切断电源，会对惯性平台上的惯性器件造成致命性损伤[5]。

为防止惯性平台倒台造成的巨大损失，利用平台弹（箭）上软件系统进行防飞算法实现，使惯性平台系统对飞转的判断更加全面、有效地预防了由于平台飞转造成的巨大损失，同时降低了平台飞转判断的虚警率，具有较高的可靠性。

1 三框架四轴惯性平台

三框架四轴平台是在原来的三轴平台的基础上，通过在最外面增加一个随动框架构成的。原来的三轴平台的外框架轴通过轴承安装在随动框架轴上，而随动框架轴通过轴承安装在弹（箭）上。这样，平台共有4个自由度，因一般相对于惯性空间的的稳定平台只需要3个自由度，因此就有一个多余的自由度，可以用来避免“框架锁定”现象。这种四轴平台在弹（箭）作大姿态角飞行时，里面的3个框架轴能始终保持相互垂直状态，因此称为全姿态稳定平台[1]，图1示出了这种平台的结构原理，其中ppp为平台坐标系，FFFYF为平台本体框架轴系。

图1 平台系统框架结构示意

2 三框架四轴平台伺服回路

惯性平台是提供空间惯性坐标系的基准, 是通过平台稳定回路实现的。稳定回路原理如图2所示。以平台轴为例，轴受干扰力矩时，台体偏离轴惯性基准。此时陀螺敏感台体偏离角度，输出电信号，经前置放大器（简称“前放”）、变换放大器等电子线路，传递为直流信号输入到轴平台力矩电机。力矩电机产生电磁力矩，抵消干扰力矩, 使台体稳定在惯性空间。

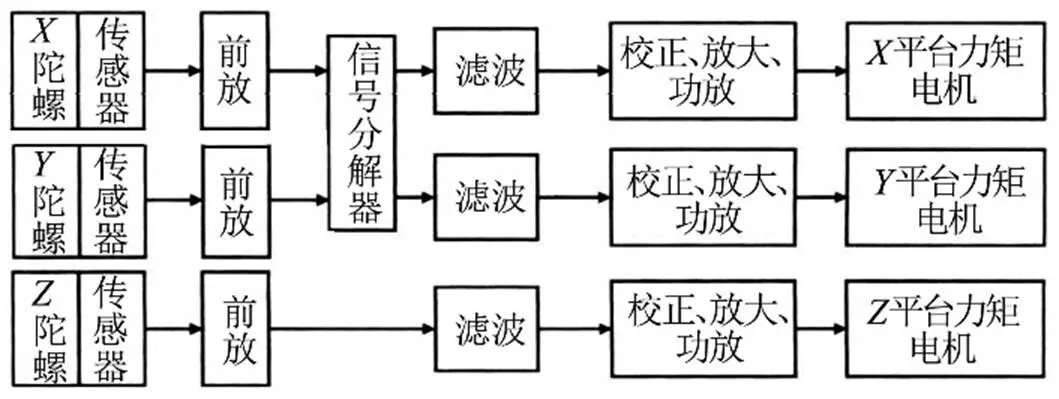
图2 平台稳定回路原理[1]

为了实现弹体全姿态飞行以及避免在特定角度时平台丢失自由度，三框架四轴平台增加了随动环，因此相对于三轴平台增加了随动环的控制功能。全姿态随动环控制方案，包括随动模式、当前位置锁定模式，随动环90°翻滚模式。随动模式时，随动框架跟随内框架运动，内框架与外框架固连，此时平台等效为由随动轴-外环轴-台体轴组成的三轴平台；当前位置锁定模式时随动框架被锁定而与基座固连，此时平台等效为由外环轴-内转轴-台体轴组成的三轴平台。在当前位置锁定模式下，由内环敏感载体在该方向上的运动；当内环角度超出预先设定的门限值后，随动环控制器进入90°翻转模式，通过将随动环翻转90°的方式将平台内环和外环敏感载体运动的方向进行调换，能够使外环离开90°，同时能使内环回到零位附近，此时，随动环控制器可重新切换到随动工作模式。

3 平台飞转原理

通过故障模式分析，可知引起平台稳定轴飞转的故障主要有：稳定/随动回路故障，动压马达未正常启动，陀螺仪输出异常，前放/解调电路故障，异常干扰力矩等。每种故障模式对应的平台稳定轴飞转情况有一定差异，其中导致飞转角加速度最大的情况为稳定或随动回路功率级输出饱和，使得弹（箭）上28 V直接加到力矩电机上，力矩电机带动平台轴加速转动。

对于平台框架：

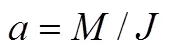
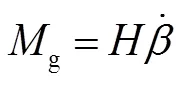
陀螺力矩相对力矩电机力矩可忽略，主要考虑摩擦力矩和力矩电机力矩引起的平台框架快速转动，并依据其进行防飞转算法的设计。

4 防飞转算法设计

对于随动回路工作在随动模式、当前位置锁定模式的四轴平台，采用传统的防飞转原理进行设计，即对姿态角进行实时检测，判断短时间内姿态角的变化率，即角速度是否超过设定的阈值。若超出，则输出保护信号。该方法的关键设计指标即为输出姿态角超速信号到判断平台飞转的时间特性。依据第3节内容，可知框架最大角加速度为

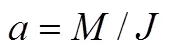
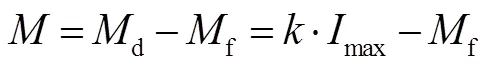
防飞设计相关参数包括：

a）耐回转角速度：陀螺仪动压马达耐回转角速度达360（°）/s；

b）转动惯量：台体轴转动惯量为0.024 kg/m2，内环轴转动惯量为0.091 kg/m2，外环轴转动惯量为 0.183 kg/m2，随动轴转动惯量为0.218 kg/m2；

c）最大干扰力矩：台体轴、内环轴最大干扰力矩不大于100 （mN·m），外环轴、随动轴大干扰力矩不大于150 （mN·m）；

依据上述参数，并考虑软件计算周期，计算各种延时条件下各轴的最大飞转角速度如表1所示。

表1 四轴最大飞转角速度

Tab.1 The Maximum Angular Velocity of Four-axis

轴名称角加速度rad/s220ms角速度(°)/s160ms角速度(°)/s200ms角速度(°)/s 台体轴31.21 35.76 286.0874357.61 内环轴8.23 9.43 75.4516394.31 外环轴6.92 7.93 63.41179.26 随动轴5.81 6.65 53.2303366.54

从表1看出，由于台体轴转动惯量较小，因此在200 ms延时条件下，角速度接近陀螺的耐回转角速度，为保证飞转判断有不小于20%余量，从输出台体轴姿态角超速信号到判断平台飞转时间最大不能超过160 ms，其它各轴的时间特性设定为200 ms即能满足要求。

飞转判据中若仅考虑框架角变化率容易导致飞转虚警，因此将力矩电机电流融合到飞转判据里进行综合判断，仅当框架角变化率达到门限值，同时力矩电机电流也同样达到最大力矩电流的80%时，判断为飞转，因此飞转判据可描述为：当随动回路工作在随动模式、当前位置锁定模式时，实时对平台台体轴、内环轴、外环轴、随动轴角速率超速信号进行判断，当有任意一个轴的角速率监测信号出现超速标识，且对应的力矩电机电流大于等于80%或小于等于-80%，台体轴连续160 ms，且内环轴、外环轴和随动轴连续 200 ms满足该条件时，则判断平台飞转，发送飞转信号。

a）当台体轴角速率监测信号出现超速标识，且外环在Ⅰ、Ⅱ象限，台体飞转方向与随动轴相反但随动轴框架角超出目标角度45°或台体飞转方向与随动轴相同时，若连续60 ms满足该条件，则判断平台飞转，发送飞转信号；

b）当台体轴角速率监测信号出现超速标识，且外环在Ⅲ、Ⅳ象限，台体飞转方向与随动轴相同但随动轴框架角超出目标角度45°或台体飞转方向与随动轴相反时，若连续60 ms满足该条件，则判断平台飞转，发送飞转信号；

c）当台体轴角速率监测信号出现超速标识，且力矩电机电流大于等于80%或小于等于-80%，若连续160 ms满足该条件，则判断平台飞转，发送飞转信号。

5 软件设计实现

根据第4节设计的防飞转算法进行软件程序的实现，软件判断周期为1 ms，其中台体轴飞转160 ms连续判断算法如图3所示。

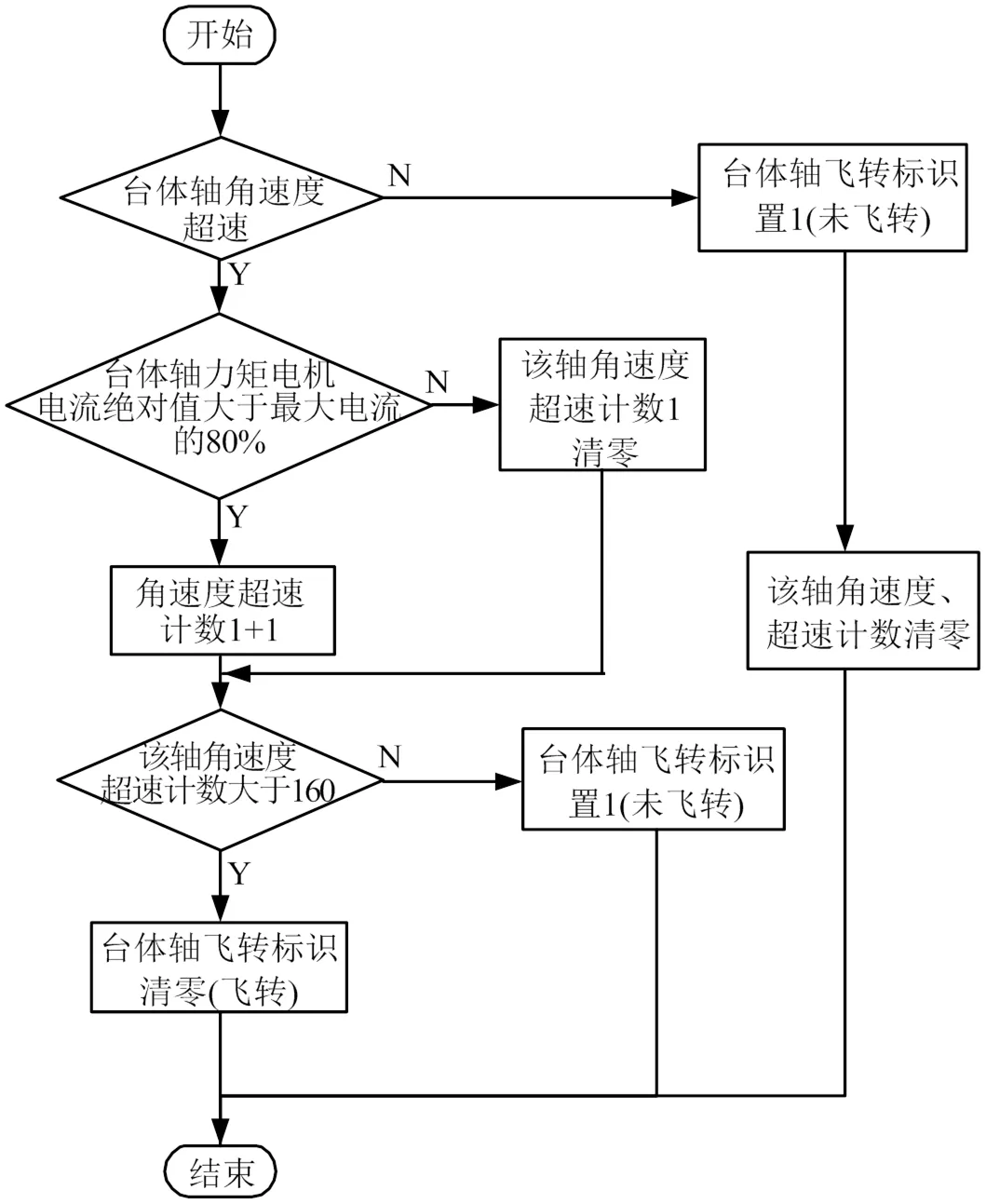
图3 随动及随锁模式下台体轴飞转判断流程

随动环90°翻滚模式时台体轴飞转判断算法如图4所示。内环轴、外环轴和随动轴飞转判断算法相同，如图5所示。飞转判断算法的总流程如图6所示。

图4 随动环90°翻滚模式下台体轴飞转判断流程

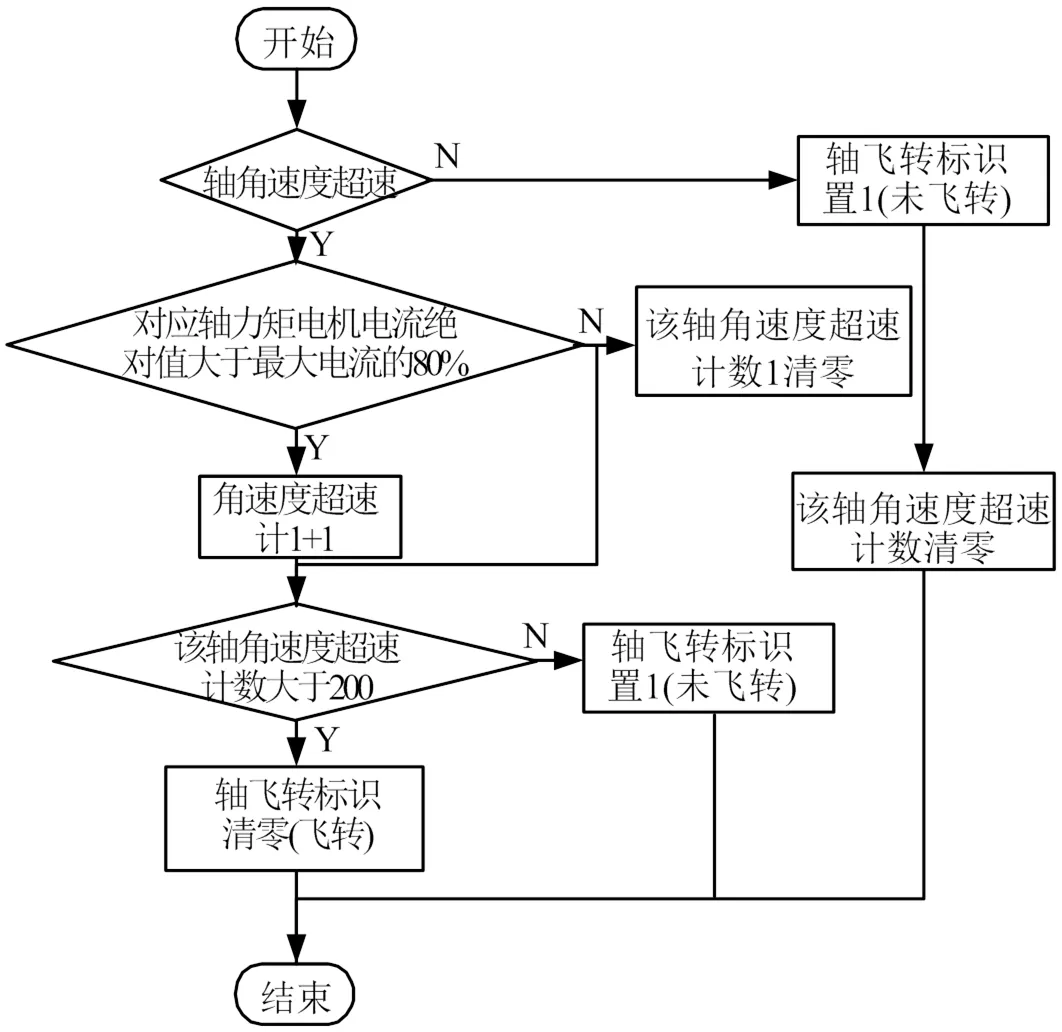
图5 内环轴、外环轴和随动轴飞转判断流程

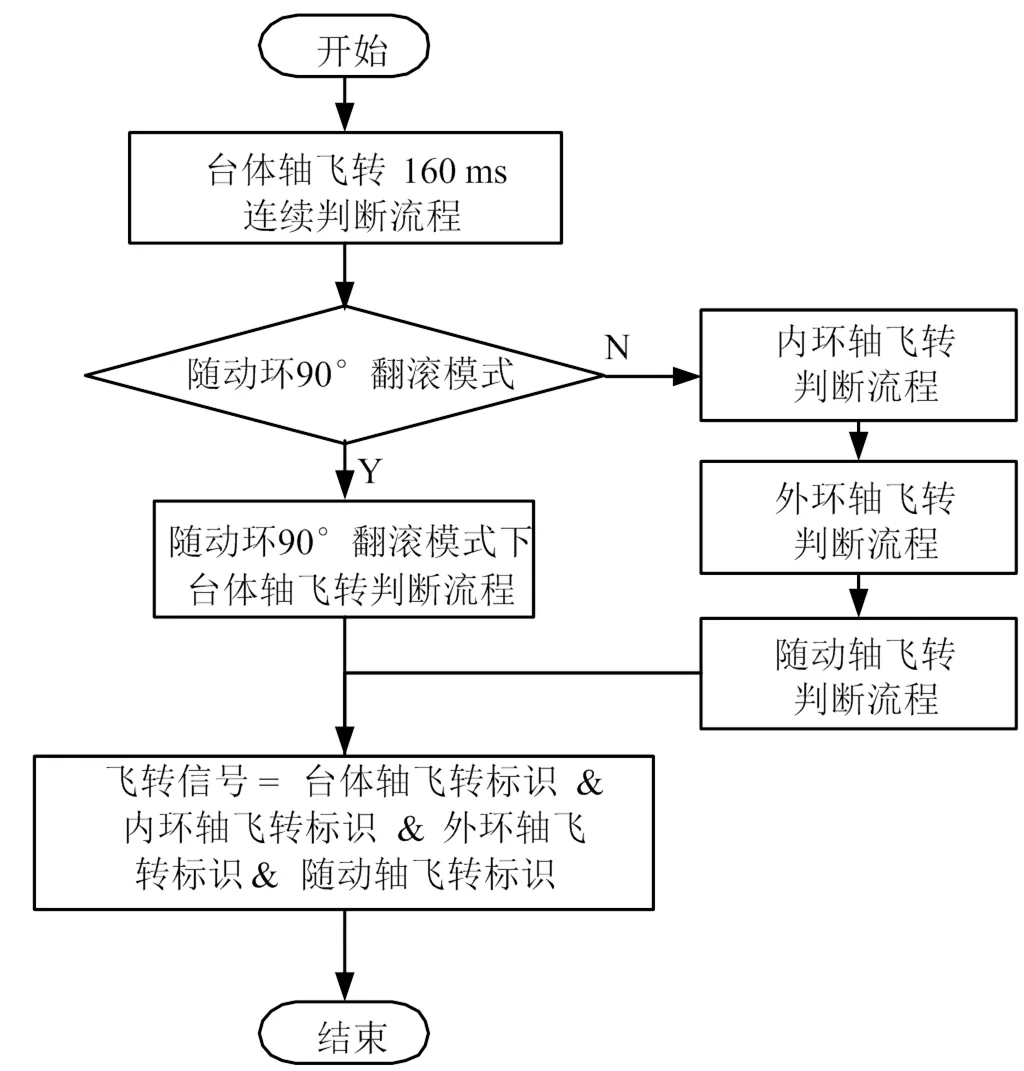
图6 飞转判断算法流程

6 实现及验证

将以上设计的飞转判断方法在某型号惯性平台系统伺服回路控制软件上进行设计实现。由RDC板通过485总线发送姿态角信息和各轴的超速信号，由伺服回路控制软件通过回路控制率计算出力矩电机电流以驱动力矩电机，并根据防飞转算法进行飞转判断，将飞转标识传递至控制系统，以及时切断回路及电源，伺服回路控制软件外部接口如图7所示。

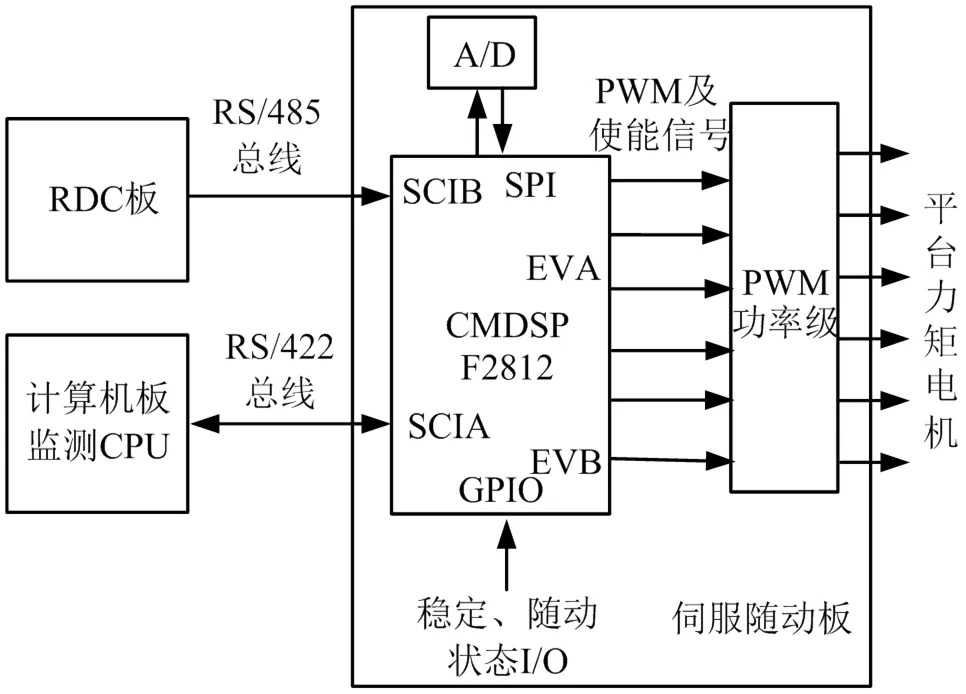
图7 伺服回路控制软件外部接口图

图8为平台飞转过程中内环框架角和随动环框架角的变化情况，内环和随动环分别在2 ms内转动了11.24°和11.3°，此时输出的超速标识及飞转标识结果如表2所示。

图8 飞转过程中框架角变化

表2 超速飞转标识

Tab.2 The Output Flag in Runaway Situation

时间/ms随动环控制模式内环轴超速标识随动轴超速标识飞转标识 0随动负向超速正向超速不飞转 20随动负向超速正向超速不飞转 40随动负向超速正向超速不飞转 60随动负向超速正向超速不飞转 80随动负向超速正向超速不飞转 100随动负向超速正向超速不飞转 120随动负向超速正向超速不飞转 140随动负向超速正向超速不飞转 160随动负向超速正向超速不飞转 180随动负向超速正向超速不飞转 200随动负向超速正向超速飞转

在上述过程中，平台外环轴和台体轴均未超速，从表2可以看出，算法能够准确地判断出平台飞转状态，满足设计要求。

7 结 论

三框架四轴平台系统飞转判断算法在前期飞转判断基础上进行了全面的整合与优化，结合稳定和随动回路数字控制原理实现了对三框架四轴平台系统飞转弹上自主判断方案。该方法经过实际平台系统验证，能够有效地对飞转状态进行判断并降低虚警率，且算法结构灵活，适应于复杂控制流程的要求。

[1] 陆元九. 惯性器件[M]. 北京: 中国宇航出版社, 1990.

Lu Yuanjiu. Inertial device[M]. Beijing: China Aerospace Press,1990.

[2] 秦永元. 惯性导航[M]. 北京: 科学出版社, 2006.

Qin Yongyuan. Research inertial navigation[M]. Beijing: Science Press, 2006.

[3] 邓益元. 静压液浮陀螺平台系统[M]. 北京: 中国宇航出版社, 2012.

Deng Yiyuan. Hydrostatic liquid-bearing gyro stabilized platform[M]. Beijing: China Aerospace Press, 2012.

[4] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2007.

Hu Shousong. Automatic control theory[M]. Beijing: Science Press, 2007.

[5] 陈乃川. 平台防飞的软件设计依据[J]. 航天控制, 1994(4): 19-21.

Chen Naichuan. The basis for designing a software to prevent a platform from runaway[J]. Aerospace Control, 1994(4): 19-21.

[6] 赵春海. 一次惯性平台失稳倒台故障分析[J]. 导弹与航天运载技术, 1999(2): 22-25.

Zhao Chunhai. The trouble analysis of an inertial platform running away because of M is-stability[J]. Missles and Space Vehicles, 1999(2): 22-25.

[7] 翟兆松, 等. 惯性平台防倒台保护电路设计[J]. 电子科技, 2010, 23(11): 77-79.

Zhai Zhaosong, et al. Design of a protection circuit to avoid collapse of the inertial platform[J]. Electronic Science and Technology, 2010, 23(11): 77-79.

[8] 孙保和, 杨朋军. 惯性平台台体动态分析及动力修改[J]. 弹箭与制导学报, 2006, 26(3): 53-58.

Sun Baohe, Yang Pengjun. Dynamic analysis and modification for inertial platform[J]. Journal of Projectiles Rockets Missiles and Guidance, 2006, 26(3): 53-58.

A Runaway Judgment Method for Three-frame and Four-axis Inertial Platform

Zhang Na, Zhao Jun-hu, Yu Zhen-yu

(Beijing Institute of Aerospace Control Devices, Beijing, 100039)

The runaway judgment method for three-frame and four-axis inertial platform is studied, the basic principle of platform runaway situation is analysed, and according to the four-axis platform characteristics the runaway judgment method is designed using software to implement this function. When the frame of inertial platform exceed the speed threshold, it can make quick runaway judgment using this method, at the same time can reduce the incidence of error. This method can make effective prevention of huge losses because of the inertial platform runaway. It is meaningful for improving the inertial platform’s reliability.

inertial platform system; three-frame and four-axis; runaway judgment

V448

A

1004-7182(2020)01-0067-05

10.7654/j.issn.1004-7182.20200112

2018-03-22；

2018-05-28

张 娜（1981-），女，研究员，主要研究方向为导航、制导与控制及嵌入式软件设计。

赵军虎（1985-），男，高级工程师，主要研究方向为导航、制导与控制及硬件电路设计。

余贞宇（1972-），女，研究员，主要研究方向为导航、制导与控制。