基于模态振型和L1正则化的结构损伤识别

2020-03-26

福建工程学院学报 2020年1期

(福建工程学院土木工程学院，福建福州 350118)

为了保障安全性，许多重大工程结构通过安装结构健康监测系统来实时监测其服役期间安全状况[1-5]。结构损伤识别是结构健康监测的重要内容，近30年，基于动力特性的损伤监测研究有了重大的进展，其基本原理为通过结构损伤前后结构模态信息的改变进行结构损伤诊断，采用的方法主要有模态应变能法[6]、模态置信度判据法[7]、曲率模态法[8]、刚度法[9]、柔度法[10]等。其中，基于有限元模型的结构损伤识别方法主要通过结构实测振动响应数据提取的模态参数或损伤特征参数，结合有限元模型，识别结构系统参数，然后进行损伤识别[11]。正则化方法是目前求解动力学反问题的主流方法，如Tikhonov正则化[12]和奇异值分解法[13]，等。这些方法的原理是基于2范数的正则化算法，存在对识别结果过度光滑的效果。而结构局部损伤的特点是突变性和稀疏性，因此可将L1范数正则化方法运用到求解结构损伤识别中的动力学反问题，提高识别精度，改善求解过程的不适应性[14-19]。

为此，本文利用结构模态振型，引入L1正则化，提出一种基于模态振型和L1正则化的结构损伤识别方法。

1 结构损伤识别方法

1.1 特征方程

无损结构用特征值方程描述结构的模态特性[14]，即：

(1)

式中，K和M分别为整体刚度矩阵和质量矩阵；ωi和Φi是无损结构的第i阶固有频率和第i阶振型；n为无损结构的振型总数。

当结构发生损伤时，其特征方程为：

(2)

1.2 单元损伤指标

以单元的刚度减少来定义损伤即：

(3)

(4)

1.3 单元损伤方程

(5)

又知单元刚度矩阵与整体刚度矩阵的关系，如下：

(6)

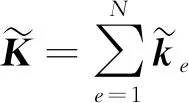
(7)

式中，N是单元总数。子矩阵ke是第e个单元对结构整体刚度矩阵的贡献。

将式(4)代入式(7)，则：

(8)

同理，第i阶振型为：

(9)

假设结构的质量矩阵在损伤前后保持不变。这种假设在大多数实际应用中是可行的。取式(5)的转置，将式(1)(8)(9)代入，得到的损伤方程如下：

i=1,…,n且j=1,…,m

(10)

式(10)可以表示为：

[S]{Δa}={ΔR}

(11)

式中灵敏度矩阵[S]的系数为：

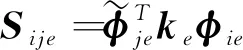
(12)

右侧残差向量ΔR为：

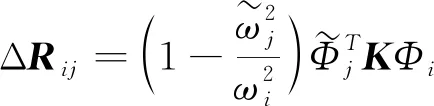
(13)

2 稀疏正则化优化算法

设原始信号为{x}，其长度为l，假设通过线性映射[17]得到长度为k的向量{y}：

{y}=[Θ]{x}

(14)

式中，[Θ]称为测量矩阵或感知矩阵，其维数为k×l。假设{x}中只有s项(s≈k≪l)非零，其他n-s项为零，当k≪l时，未知数远多于方程数，故式(14)为欠定方程组。

根据稀疏恢复理论，{x}可以通过式(15)优化求解：

(15)

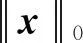
利用l1范数代替l0范数，将式(15)的非凸组合优化问题转化为凸松弛问题求解：

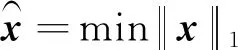
(16)

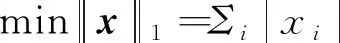
实际应用中，多数信号近似稀疏，而且信号测量过程中由于硬件设备等原因会引入噪声，当测量存在噪声时，压缩感知测量过程表示为：

{y}=[Θ]{x}+e

(17)

式中，e为测量误差。

x可通过求解如下l1优化问题进行重构：

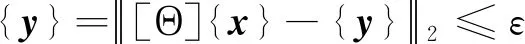
(18)

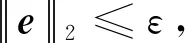
由式(11)可进一步得到[15,16]：

[S]{Δa}={ΔR}={R0}-{RE}

(19)

式中，{R0}为无损结构测得的特征值，{RE}为损伤结构测得的特征值。

式(19)建立了结构单元损伤刚度变化系数向量{Δa}与测试的结构模态参数直接的关系，但{Δa}的维数远大于测点数目，即未知数远多于方程数，式(19)为一病态的线性方程组，考虑到结构单元损伤向量{Δa}具有稀疏性，只有少数损伤的结构单元其值为非零，因此可通过式(20)优化求解：

(20)

将式(19)代入(20)中：

(21)

式中，R({Δa})=[S]{Δa}+{RE}。

式(21)可转化为无约束最小化问题：

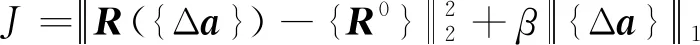
(22)

式中，拉格朗日乘子β为正则化参数且大于0。

一般采用优化方法求解式(22)，传统的模型修正方法是采用L2正则化方法，即：

(23)

采用L2正则化方法常常导致结果过于光滑，这与实际损伤的稀疏性不符，为此，本文采用式(22)作为收敛方程，且考虑到损伤值的非负性，增加限定条件0≤Δa≤1。

3 数值算例分析

3.1 简支梁数值模拟

建立简支梁有限元模型，简支梁总长6 m，含15个单元，弹性模量E=32 GPa，密度ρ=2 500 kg/m3。模型如图1所示。

为了研究方法的有效性，设置种损伤工况，工况模拟见表1。其中，结构损伤主要根据模拟刚度降低。为了研究噪声的影响，本文在工况3中对振型添加了1%的噪声水平，即：

z=za×(1+εR)

(24)

式中，za和z分别代表原始信号和噪声污染后的振型；R是均值为0，偏差为1的正态分布随机数；ε是噪声水平为1%。

正则化参数β采用L曲线法确定，取0.1。

图1 简支梁模型Fig.1 Model of the simply-supported beam

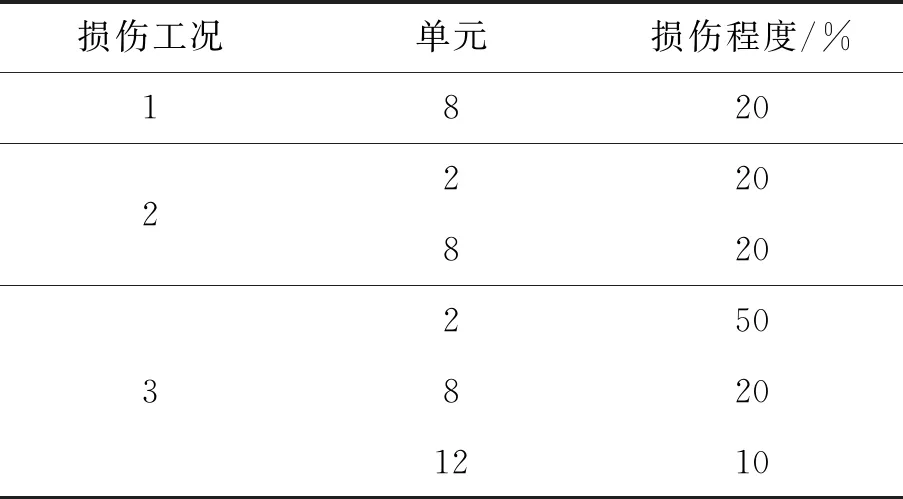
表1 损伤工况模拟

3.2 计算结果

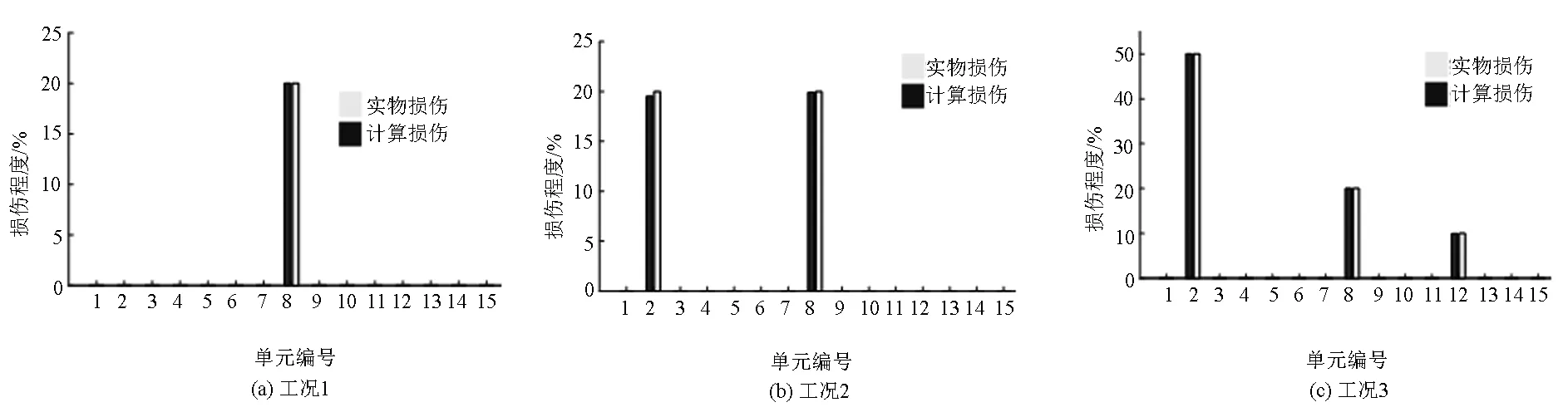
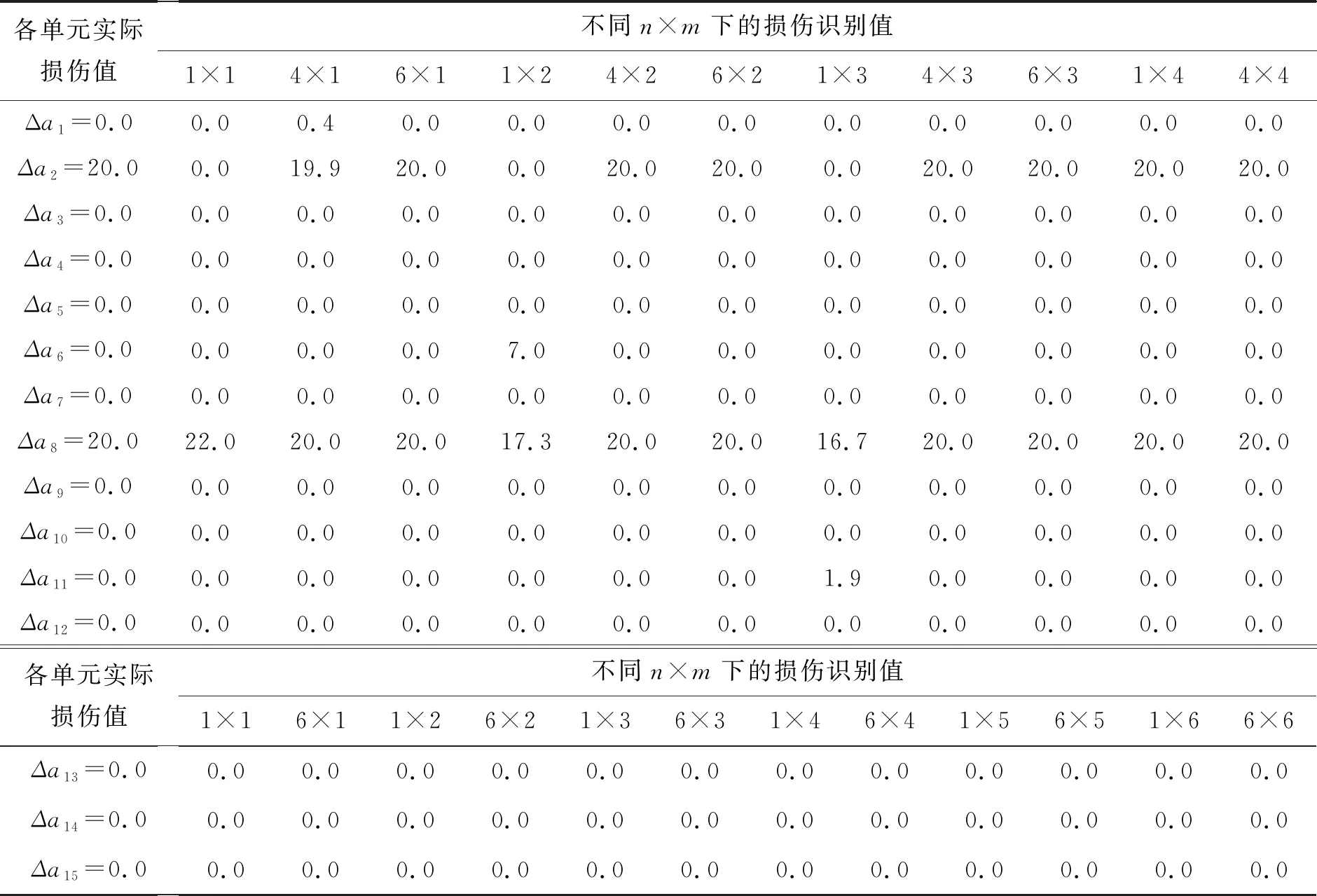
取n=4个，m=3个((n×m)

3.3 振型数对识别影响分析

为进一步研究无损结构的振型数n、损伤结构的振型数m以及二者的总振型数对损伤识别结果的影响对3种损伤工况展开分析。

图2 3种损伤工况下的损伤识别结果Fig.2 Identified damage results of three cases

表2为无损结构的振型数n∈[1,6]，损伤结构的振型数m∈[1,6]时工况1的识别结果。从表2可以看出，针对单损伤工况，无损结构和损伤结构的振型数对识别结果均无影响，基于L1正则化的损伤识别方法均可精确地识别结构损伤。

表3为损伤工况2在不同振型数下的损伤识别结果。从表3可见，当n×m为1×1，1×2，1×3时，单元2识别值的相对误差达到100%，识别错误。分析原因为n与m的值均较小时，提供信息较少，且损伤单元有2个，工况较为复杂，故识别结果较差。对于剩余振型数，单元2和单元8的识别误差最大分别为0.5%和16.5%，均小于20.0%，且大多数情况相对误差为0，故本文方法可以较准确地识别出损伤位置与损伤程度。

表4为损伤工况3在不同振型数下的损伤识别结果。从表4可知，当损伤结构的振型数为1或无损结构的振型数为1时，识别误差为100%，但当n×m>4时，不再出现识别值为0的情况，随着n和m的不断增加，识别精度逐渐提高。当n×m≥6时，单元2检测值的最大误差为0.8%，单元8检测值的最大误差为0.5%，单元12检测值的最大误差为2%，均小于20%，处于可接受的范围。故建议通过本文所提方法进行结构损伤识别时，n×m可取大于等于6。