用分位数回归建立的混交林树高生长模型1)

2020-03-26赵梦草顾海燕

东北林业大学学报 2020年2期

赵梦草顾海燕

(东北林业大学，哈尔滨，150040)

与分位数有关的回归方法已经有很长的统计学历史，最早由Roger et al.[1]于1978年提出。分位数回归能够描述除中心位置外任意发散点处变量的变化趋势，较经典的最小二乘回归具有独特的优势。目前，分位数回归在国内外林业界得到了广泛的应用：高慧淋等[2]利用Reineke方程和线性分位数回归技术，建立了不同分位点的长白山落叶松人工林最大林分密度与林木平均胸径的关系模型；Ramazan et al.[3]依据h-d模型评价了固定、校准固定和校准混合效应模型、三分位数和五分位数回归5种替代建模方法。Paula et al.[4]开发了桉树人工林的h-d方程，研究了Harrison方程和配有迭代重加权最小二乘法。Som et al.[5]将分位数回归系统运用到对树木直径增长函数的研究中，比较了混合效应模型、九分位数、五分位数、三分位数四种回归方法。本文利用分位数回归，研究影响树高的因素并对其影响程度的大小进行分析，为混合林的经营策略提供参考。

1 研究区概况

研究地区位于黑龙江省大兴安岭地区新林区北部翠岗地区，海拔1 000～1 400 m，地理坐标北纬43°～53°30′，东经117°20′～126°。大兴安岭为寒温带大陆性季风气候，被称为中国的“寒极”，南北气候差异明显，由北向南年均温为-5.7～4.0 ℃，年降水量北部为400～500 mm、南部及部分西坡小于400 mm。森林覆盖率达86.6%，木材蓄积量占全省26.6%，占全国7.8%；树种以兴安落叶松和樟子松为主。

2 研究方法

2.1 分位数回归

分位数回归是回归分析的方法之一。分位数是指将一个随机变量的概率分布范围分为几个等份的数值点。分位数回归是给定回归变量、估计响应变量条件分位数的一个基本方法，不仅可以度量回归变量在分布中心的影响，而且还可以度量在分布上尾和下尾的影响，进一步推论因变量的条件概率分布。

线性分位数回归的基本公式为：

(1)

式中：xi为第i个回归变量；X=(1，x1，x2，…，xm)T是m+1维向量；b=(β0(τ)，β1(τ)，…，βm(τ))T；τ为分位数；系数回归常数和回归系数为β0(τ)、β1(τ)、…、βm(τ)。

2.2 数据处理

选择翠岗地区的4块落叶松白桦混交林样地，实测样地内所有林木的树高、胸径、活枝高及树冠东、南、西、北的冠幅，共获得677组数据，分析不同τ的胸径、活枝高及树冠东、南、西、北冠幅与树高的关系。

由图1、图2可见：树冠东、南、西、北的冠幅与树高的关系，在不同τ没有十分明显的区别，因此重点采用分位数回归研究胸径、活枝高与树高的关系。统计研究的3个变量的基本信息见表1；其中间伐组实行三年一次间隔的弱度间伐。

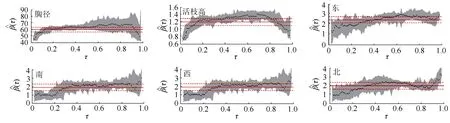
图中纵坐标表示不同分位数回归系数的参数估计值图中阴影部分表示的95%的置信域。

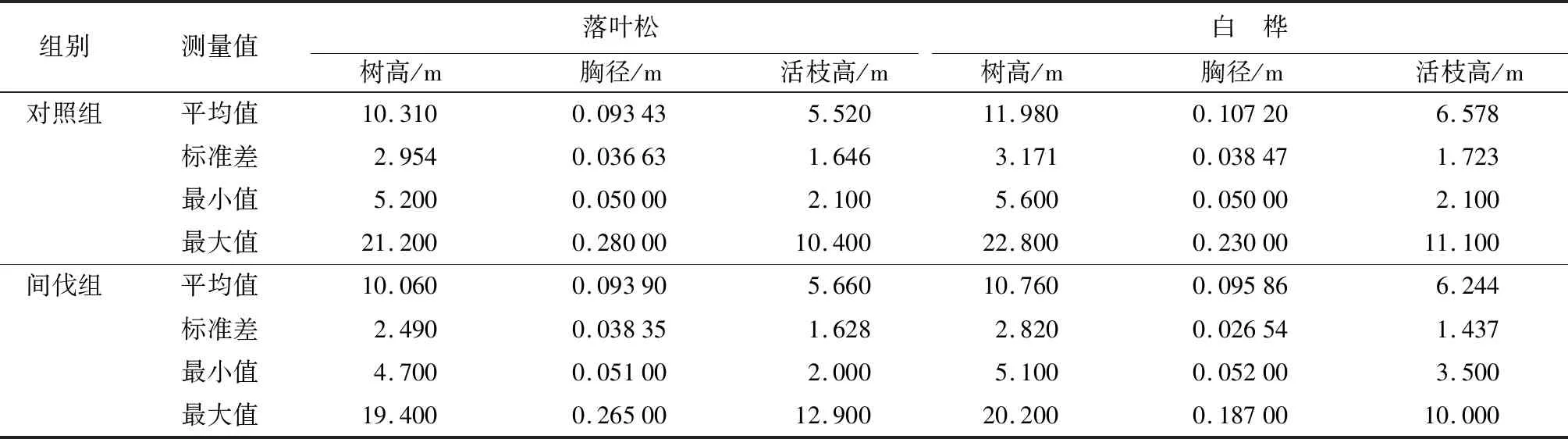
表1 树木特征因子统计

3 结果与分析

3.1 胸径、活枝高与树高的相关性

由表2可见：胸径、活枝高与树高都有较强线性关系，因此用线性模型分析比较合适。

3.2 胸径与树高关系的分位数回归

由于树高与胸径呈现线性趋势，因此采用一元线性分位数回归模型，利用公式QY(τ|x)=β0(τ)+xβ1(τ)，τ∈(0，1)，x为胸径，所得参数估计值见表3。

表2 胸径、活枝高与树高的相关系数

表3 树高与胸径关系的分位数回归参数估计值

由表3可见：落叶松对照组，在τ=0.10，树高增加最多，胸径每增加1 cm，树高增加约67.3 cm；在τ=0.90，树高增加最少，胸径每增加1 cm，树高增加约50.7 cm；由最小二乘法得到，胸径每增加1 cm，树高平均增加约64.2 cm。落叶松间伐组，在τ=0.50，树高增加最多，胸径每增加1 cm，树高增加约56.8 cm；在τ=0.90，树高增加最少，胸径每增加1 cm，树高增加约45.6 cm；由最小二乘法得到，胸径每增加1 cm，树高平均增加约50.4 cm。

由表3可见：白桦对照组，在τ=0.90，树高增加最多，胸径每增加1 cm，树高增加约89.6 cm；在τ=0.10，树高增加最少，胸径每增加1 cm，树高增加约51.0 cm；由最小二乘法得到胸径每增加1 cm，树高平均增加约64.6 cm。白桦间伐组，在τ=0.75，树高增加最多，胸径每增加1 cm，树高增加约70.5 cm；在τ=0.25，树高增加最少，胸径每增加1 cm，树高增加约51.4 cm；由最小二乘法得到，胸径每增加1 cm，树高平均增加约61.8 cm。

图3表示树高与胸径关系的分位数回归直线，直线的斜率代表不同分位数下树高随胸径变化的平均变化率。发现不同分位数的树高随胸径的变化是不同的，因此利用分位数回归能更全面地看出树高与胸径的关系。

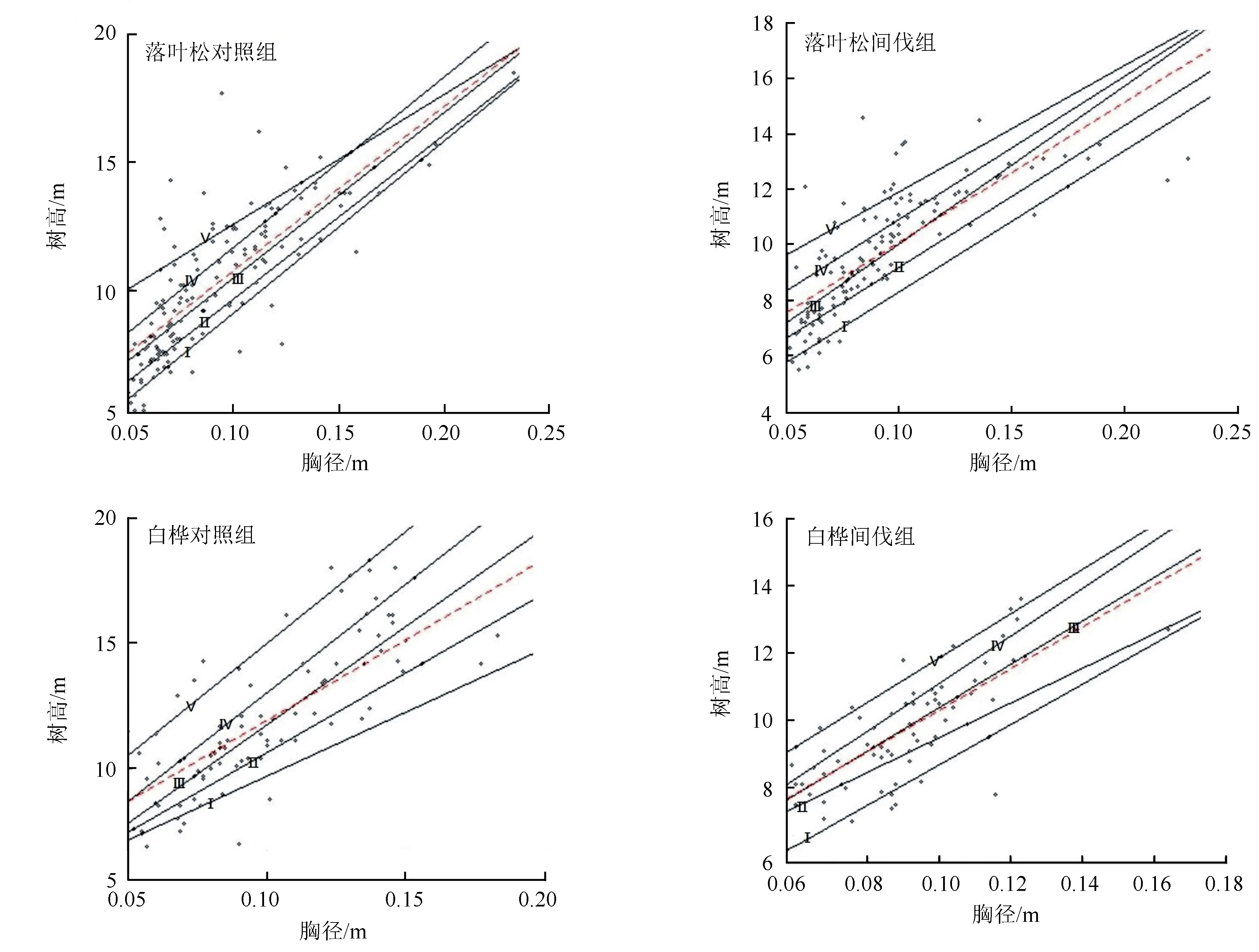
Ⅰ～Ⅴ分别是τ为0.10、0.25、0.50、0.75、0.90的分位数回归直线，虚线为最小二乘回归直线。

3.3 活枝高与树高关系的分位数回归

由于树高与活枝高呈现线性趋势，因此也采用一元线性分位数回归模型，利用公式QY(τ|x)=β0(τ)+xβ1(τ)，τ∈(0，1)，x为活枝高，所得参数估计值见表4。

表4 树高与活枝高关系的分位数回归参数估计值

由表4可见：落叶松对照组，在τ=0.75，树高增加最多，活枝高每增加1 m，树高增加约1.8 m；在τ=0.10，树高增加最少，活枝高每增加1 m，树高增加约1.4 m；由最小二乘法得到，活枝高每增加1 m，树高平均增加约1.5 m。落叶松间伐组，在τ=0.50，树高增加最多，活枝高每增加1 m，树高增加约1.3 m；在τ=0.10，树高增加最少，活枝高每增加1 m，树高增加约1.0 m；由最小二乘法得到，活枝高每增加1 m，树高平均增加约1.1 m。

由表4可见：白桦对照组，在τ=0.90，树高增加最多，活枝高每增加1 m，树高增加约1.7 m；在τ=0.10，树高增加最少，活枝高每增加1 m，树高增加约1.3 m；由最小二乘法得到，活枝高每增加1 m，树高平均增加约1.5 m。白桦间伐组，在τ=0.50，树高增加最多，活枝高每增加1 m，树高增加约1.4 m；在τ=0.25，树高增加最少，活枝高每增加1 m，树高增加约1.3 m；由最小二乘法得到，活枝高每增加1 m，树高平均增加约1.4 m。

图4表示树高与活枝高关系的分位数回归直线，直线的斜率代表不同分位数下树高随活枝高变化的平均变化率。发现不同分位数的树高随活枝高的变化是不同的，因此利用分位数回归能更全面地看出树高与活枝高的关系。

Ⅰ～Ⅴ分别是τ为0.10、0.25、0.50、0.75、0.90的分位数回归直线，虚线为最小二乘回归直线。

3.4 胸径、活枝高与树高关系的分位数回归

利用二元线性分位数回归模型进行回归，QY(τ|x)=β0(τ)+x1β1(τ)+x2β2(τ)，τ∈(0，1)、x1为胸径、x2为活枝高，所得参数估计值见表5。由表5可见，同一样本数据，不同τ得到的参数估计值不同，分位数回归比最小二乘法能够更多的反映数据的局部信息。

表5 落叶松树高分位数回归参数估计值

图5为不同τ时落叶松树高随胸径、活枝高变化趋势，τ∈(0，1)，间距为0.05，共有19个点。由图5可见：树高随胸径的线性增加变化，对照组总体呈上升趋势，间伐组变化较为平缓；树高随活枝高的线性增加变化，对照组总体较为平缓，间伐组变化呈上升趋势；在τ=0.95处，对照组和间伐组树高随胸径和活枝高的线性增加变化都较小。图5中两图的虚线表示由最小二乘法得到的参数估计，对照组，胸径每增加1 cm，树高约增加47.3 cm；活枝高每增加1 m，树高约增加69 cm。间伐组，胸径每增加1 cm，树高约增加33.1 cm；活枝高每增加1 m，树高约增加64 cm。

表6为白桦树高线性分位数模型在不同τ时得到的参数估计值。

τ∈(0，1)，间距为0.05，共有19个点；虚线表示由最小二乘法得到的参数估计。

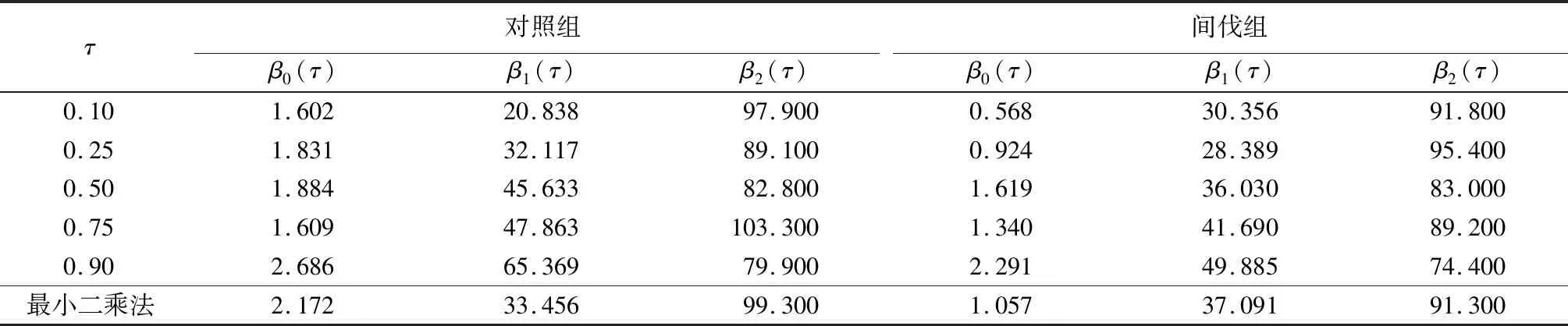
表6 白桦树高分位数回归参数估计值

由图6可见：树高随胸径的线性增加变化，对照组和间伐组均呈上升趋势；树高随活枝高的线性增加变化，对照组和间伐组变化均呈下降趋势。图6中两图的虚线表示由最小二乘法得到的参数估计，对照组，胸径每增加1 cm，树高约增加33.5 cm；活枝高每增加1 m，树高约增加0.99 m；间伐组，胸径每增加1 cm，树高约增加37.1 cm；活枝高每增加1 m，树高约增加0.91 m。

4 结论与讨论

本文利用分位数回归研究了树高、胸径和活枝高的相关关系。在一元线性分位数回归模型中，落叶松胸径对树高的影响在低尾处较明显，而白桦胸径对树高的影响在高尾处较明显，两树种对照组胸径每增加1cm，树高增加的高度都明显高于间伐组；落叶松和白桦活枝高对树高的影响均在中高尾处较明显，两树种对照组活枝高每增加1m，树高增加的高度都明显高于间伐组。在二元线性分位数回归模型中，落叶松和白桦胸径对树高的影响均在高尾处较明显，而落叶松和白桦活枝高对树高的影响均在低尾处较明显，两树种对照组胸径对树高的影响以及活枝高对树高的影响均明显强于间伐组。在树高、胸径和活枝高的相关关系中，单个因素的影响规律与多个因素相比具有一定的差异，追求更加精准的分析应适当选取影响程度大的一些影响因素综合进行分析。