基于连清样地数据的全国杉木人工林平均木树高.胸径模型
2023-04-29牛思圆刘鹏举雷相东等
牛思圆 刘鹏举 雷相东等


关键词:连清样地数据;杉木;树高.胸径模型
中图分类号:S757 文献标志码:A 文章编号:1001-1498(2023)01-0117-07
杉木(Cunninghamia lanceolata(Lamb.)Hook.)是我国主要造林树种之一,关于杉木树高·胸径模型,很多学者都开展过研究,但多为小区域建模。沈子奕等以江西省青原山杉木人工林为研究区,在基础模型上构建了混合效应模型,结果表明,加入地形因子的混合效应模型能够更好的拟合该地区树高·胸径关系。魏晓慧等利用福建省三明市将乐县国有林场的杉树人工林调查数据,对Richards方程进行拟合,得出Richards模型能够提高拟合精度的结果。黄其城选择4个常用的相对树高曲线模型对福州市8个国有林场60片伐区的树高·胸径调查数据进行拟合,最终确定Richards函数变形固定参数模型作为杉木相对树高曲线的最优模型。近年来,在树高-胸径模型的构建中逐渐加入了如海拔、林分密度、土壤条件、立地条件等随机效应,用混合模型的方法来提高模型的拟合精度,但是这些模型大多都基于林场等小区域建模,在实际应用时需要重新求解随机效应参数,限制了模型的应用。在某一地区建立的模型,难以推广到其他地区,并且仍有杉木非核心分布区树高-胸径模型缺失,因此建立大区域乃至全国大尺度杉木树高·胸径模型显得尤其重要。目前,大区域的杉木树高一胸径模型在我国的研究还较少,如覃阳平等选用Richards等15种树高-胸径模型作为候选模型,建立了云南省5个针叶树种的树高-胸径模型,其中杉木的最优模型为Hossfeld方程。李海奎等分别采用树高分级和未分级的方法,建立了杉木等6个我国主要树种的树高曲线模型,结果表明分级建模方法的精度显著优于未分级建模。
因此,为推进我国杉木大尺度区域建模方面的研究,本研究基于第六次、第七次全国森林资源连续清查固定样地数据,以全国15个省份的杉木人工林为研究对象,选用18种常见的生长模型作为候选模型,分别拟合杉木树高胸径的关系,分省区建立杉木人工林最优平均木树高·胸径模型。
1数据来源与处理
1.1研究区概况
杉木人工林主要分布于我国的15个省区,分别为江苏、安徽、河南、浙江、福建、江西、湖北、湖南、广东、广西、重庆、四川、陕西、贵州和云南,为了便于应用,本研究分省区建立杉木树高·胸径模型,但由于一些省份杉木样地数据过少,参考张英凯等杉木分布区分组的结果,对低于100个观测数据的省份进行合并处理。江苏省和安徽省均位于长江中下游平原,河南省的杉木样地分布于该省东南部,紧邻安徽省杉木分布区,且3省的杉木分布区气候都属亚热带季风气候,因此将江苏、安徽和河南3省数据合并处理(以下简称苏徽豫),一同建模。陕西省杉木样地主要分布在该省秦岭南部地区,紧邻重庆市北部的杉木样地,因此将陕西省数据与重庆市数据合并处理(以下简称渝陕),其余各省区单独处理。
1.2数据来源
所用数据来自于第六次、第七次一类清查杉木人工林固定样地数据的树高调查表,每个固定样地选取3~5株胸径接近样地平均胸径的树木测定其树高,剔除不完整的样本,最终总样本数为23239个平均木单株树高一胸径数据。详细的数据统计量如表1所示。
2研究方法
2.1建模方法
根据前人的研究经验,采用常见的18个线性和非线性模型作为候选模型来拟合杉木的树高·胸径关系,探讨杉木各省区最适宜的树高曲线形式,候选树高·胸径模型的具体表达式如表2所示。
2.2模型评价及检验
模型的评价主要利用决定系数(R2)、平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)和平均预估误差(MPE)5种评价指标,分析残差分布图,并考虑模型各参数的生物学意义以及参数的取值范围是否合理,以此来确定各省区拟合效果最优的模型。R2的值越接近1,MAE、MRE、RMSE和MPE的值越小,说明该模型拟合精度越高。
在确定各省区最优模型后,模型验证部分采用5折交叉验证法,具体步骤为:首先将全部数据平均分成5份,每次从5份数据中拿出4份用来建模,剩下的1份作为验证数据,重复进行5次,共建模5次得到5个子模型,应用5个子模型的交叉检验估计值计算各误差指标,依据MAE、MRE、RMSE和MPE越小越好的原则,来评价选择的各省区最优模型的预测能力。
3结果与分析
3.1最优模型的筛选
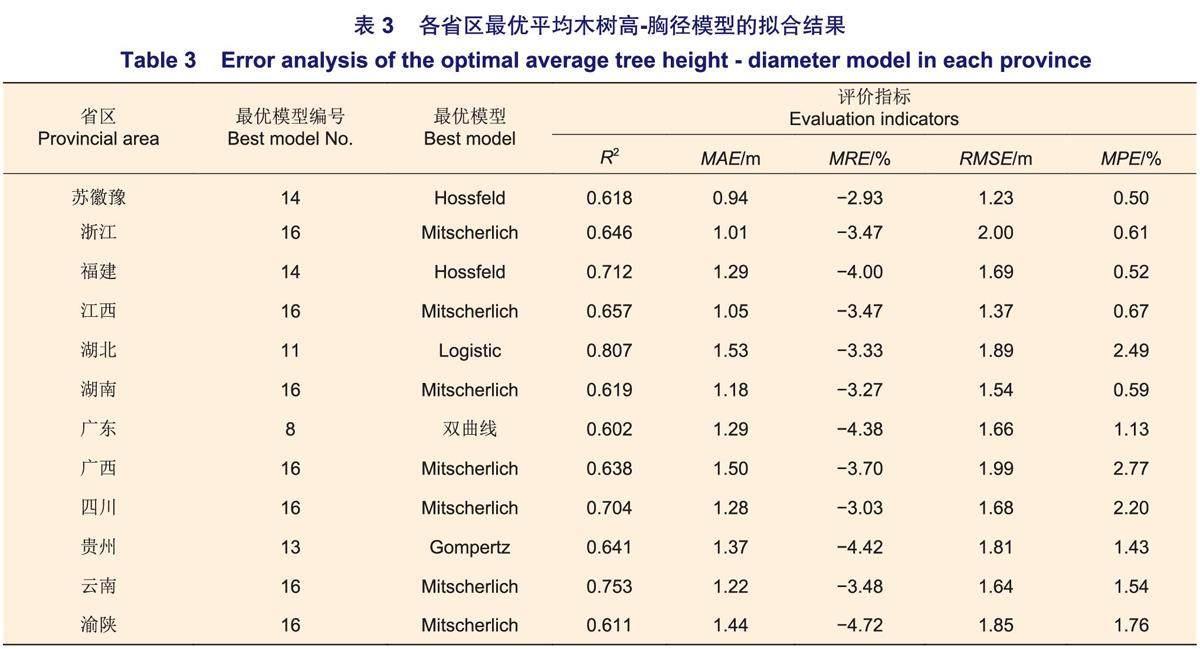
最优模型的选取遵循模型拟合精度最高同时误差最小的规则,综合权衡R2,MAE,MRE、RMSE和MPE 5个指标,以及模型参数的取值是否符合生物学规律,得出各省区最优树高·胸径模型。各省区最优平均木树高·胸径模型建模结果和误差分析见表3。可以看出,各省区最优模型并不相同,最优模型以模型16(Mitscherlich方程)为主,各省区的拟合结果均具有较高的精度,每个省区最优模型的R2介于0.602~0.807之间,MAE介于0.94~1.53 m之间,MRE介于-2.93%~-4.72%之间,RMSE介于1.23~2.00 m之间,MPE介于0.50%~2.77%之间。江苏省、安徽省和河南省的MAE最小,各省的MRE均小于±5%,RMSE均小于2.00 m,MPE均小于3%。其中湖北省最优模型拟合结果精度最高,最优模型为模型11(Logistic方程),R2达到0.807,MAE,MRE,RMSE和MPE分别为1.53 m,-3.33%,1.89 m,2.49%;广东省最优模型的拟合结果精度最低,R2为0.602,MAE,MRE,RMSE和MPE分别为1.29 m,-4.38%,1.66m,1.13%.
15个省区最优模型的树高预测值-残差的分布如图1所示,残差点较为平均地落在残差值为0的标准线的上下两端,大部分都分布在±4的残差值之内,也有少数残差值较大的样本,但并无明显的异质性,表明模型的拟合效果较好,能够应用于实际的拟合预测。
3.2模型的评价与验证结果
为检验模型的适用性,采用5折交叉验证法对各省区5次建模的最优模型预测能力进行检验,用5个子模型的交叉检验估计值计算相关误差指标,得到各省区的误差精度指标以及建模结果见表4。从表4可以看出,MAE在0.94~1.57 m之间,MRE在-2.93%~-4.65%之间,RMSE在1.23~2.00 m之间,MPE在0.41%~2.77%之间,各省区最优模型的检验结果大体与建模数据的分析结果一致,同时所有模型的MRE在±5%以内,满足精度要求,MAE均在2.00 m以内,RMSE均小于或等于2.00 m,MPE均小于3%,说明模型预测效果好,所有模型的误差较小,得出的15个省区的最优树高·胸径模型有较强的适用性,可以在实际中应用。
4讨论
树高·胸径模型是立地质量评价和反演复杂模型的基础。不同于以往的杉木小区域建模,本研究建立了杉木人工林分布的各省区的大尺度的树高生长模型。小区域建模的研究范围一般为林场或区县,数据量较少,受环境差异影响较小,虽然适用范围有限,但模型精度相对较高,R2通常在0.8以上。大尺度建模研究区域一般在整个省乃至全国范围内,所用数据量较大,适用范围广泛,但省内或全国范围内各地环境存在差异,因此建模精度相对较低,R2通常分布在0.6~0.8之间。本研究建立的各省区模型R2在0.610~0.834之间,平均值为0.679,建模精度在上述有关学者的大区域杉木建模精度范围内,因此本研究建立的各省区的杉木树高一胸径生长模型可以预测不同径阶杉木的树高情况。本研究评价指标中,平均相对误差(MRE)没有绝对值,因此是存在正负的,正值表示实测值大于预测值,负值表示实测值小于预测值,本研究MRE均为负数,表明拟合模型的预测结果大部分都大于实测值,但MRE整体均分布在±5%之间,结果符合精度要求。
交叉验证在模型检验中应用广泛,操作简便,本研究验证,部分采用了5折交叉验证法,充分利用样本数据,能够更准确地检验选出的最优模型的预测能力,但是交叉验证的折数是可以改变的,不同折数不仅决定着建模和检验样本的多少,还影响着误差指标的结果和计算的复杂程度,本研究为便于计算,选用了5折交叉验证法,在未来的研究中,可尝试10折交叉验证或其他验证方法进行验证。
本研究只考虑了杉木树高与胸径的关系,只有胸径一个自变量,应用范围较广泛。同时,杉木树高的生长情况还受多种因素影响,如海拔高度、林分密度、气象条件、立地条件、经营目标、抚育间伐等,未来可以尝试建立包含多种林分因子(包括因子间的相互作用)的广义树高,胸径模型,也许可以进一步提高模型的精度。由于本研究采用了两期数据,存在相关性,未采用混合效应模型,因为混合效应模型需要进行新的随机参数估计,会限制其在实际中的应用。另外,本研究为便于模型的实际应用,按行政区划进行建模,未比较不同省份之间回归模型的差异显著性,将来可在差异比较的基础上,将差异不显著的省份合并建模,尝试利用杉木产区划分进行建模。
5结论
本研究基于第六次、第七次全国森林一类清查固定样地数据,以杉木人工林分布的15个省区为研究区,利用18种基础生长方程,分别对各省区杉木平均木树高.胸径数据进行拟合,然后根据模型的决定系数(R2)、平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)和平均预估误差(MPE)这5个评价指标,并参考树高预测值·残差分布图,最终决定各省区适宜的模型,建立了全国杉木各省区平均木树高-胸径关系模型。结果表明:各省区的最优平均木树高-胸径模型不尽相同,模型的决定系数R2在0.602~0.807之间,MAE在0.94~1.53m之间,MRE在-2.93%~-4.72%之间,RMSE在1.23~2.00 m之间,MPE在0.50%~2.77%之间。经检验,模型拟合效果较好,参数取值范围合理,对于杉木树高一胸径的拟合效果较好,可以作为全国各省区基本的最优杉木人工林平均木树高-胸径模型。
