An Indirect Finite Element Method for Variable-Coeffi cient Space-Fractional Diff usion Equations and Its Optimal-Order Error Estimates

Xiangcheng Zheng · V. J. Ervin · Hong Wang

Abstract We study an indirect f inite element approximation for two-sided space-fractional diff usion equations in one space dimension. By the representation formula of the solutions u( x) to the proposed variable coeffi cient models in terms of v( x), the solutions to the constant coeff icient analogues, we apply f inite element methods for the constant coeffi cient fractional diff usion equations to solve for the approximations v h(x) to v( x) and then obtain the approximations u h(x) ofu(x) by pluggingv h(x) intotherepresentation ofu( x).Optimal-orderconvergence estimatesof u (x)-uh(x)are provedinboth L2 and Hα∕2norms. Several numerical experiments are presented to demonstrate the sharpness of the derived error estimates.

Keywords Fractional diff usion equation · Finite element method · Convergence estimate

1 Introduction

Fractional differential equations (FDEs) provide adequate descriptions of challenging phenomena such as the anomalously diff usive transport and nonlocal spatial interactions [ 2,16]. However, FDEs present new mathematical issues that are not common in the context of integer-order diff usion equations. In this paper, we take a relatively simple onedimensional space-fractional differential equations (sFDEs) to address some of the issues and demonstrate how we develop an indirect f inite element method to overcome these diffi culties.

Ervin and Roop [ 5] f irst carried out a rigorous analysis of the Dirichlet boundary-value problem of the constant coeffi cient sFDEs of order 1＜α＜2 in one space dimension:

Here, the parameter 0≤r≤1 indicates the relative weight of forward versus backward transition probability, D refers to the f irst-order differential operator, and the left and right fractional integrals of order 0＜σ＜1 are def ined as [ 18, 19]

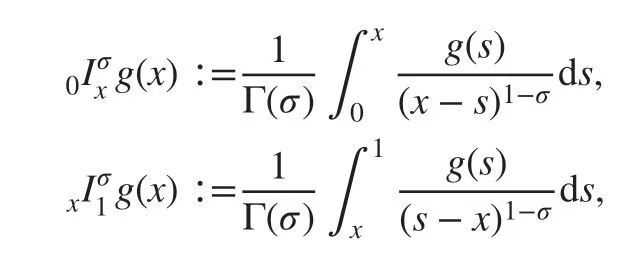
where Γ(·) is the Gamma function.

They derived the following Galerkin weak formulation for problem ( 1): f ind u∈(0,1) such that

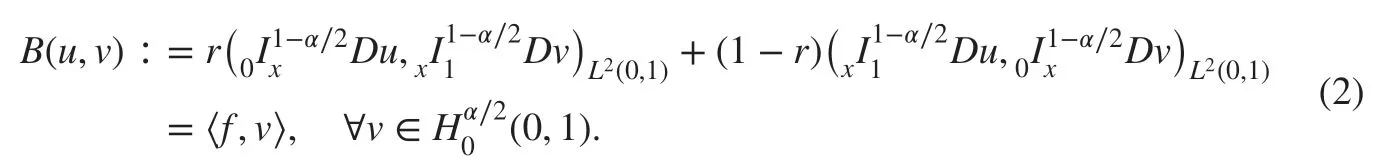
They proved that the bilinear form B(·,·) is coercive and continuous inand so the wellposedness of the Galerkin weak formulation ( 2).

Furthermore, Ervin and Roop went on to def ine a family of f inite element methods for problem ( 1) based on the Galerkin weak formulation ( 2) and proved the following optimal-order error estimate for the f inite element approximation uh∈(0,1) in the energy norm under the assumption that the true solution u to problem ( 1) belongs to

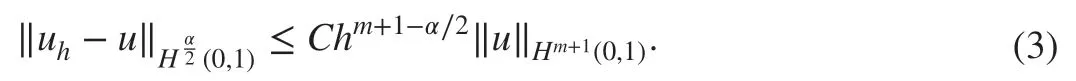
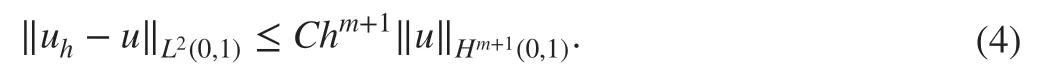
Subsequently, these techniques were extended to the mathematical analysis of multidimensional problems, time-dependent problems as well as other numerical methods. While these error estimates are in parallel to these integer-order analogues [ 4], it was realized subsequently that there are actually signif ciant differences between FDEs and their integerorder analogues. Here, we illustrate some of them.

The homogeneous Dirichlet boundary-value problems of one-dimensional linear elliptic sFDEs with smooth coeffi cients and source terms yield solutions with singularities. It was shown in [ 13, 22, 23] that the solutions to the homogeneous Dirichlet boundaryvalue problems of the one-dimensional linear elliptic sFDEs with constant coeffi cients and source terms exhibit boundary layer singularities. In other words, the smoothness(e.g., in Sobolev or Hölder spaces) of the coeffi cients and right-hand sides of linear elliptic sFDEs in one-space dimension cannot ensure the smoothness of their solutions in corresponding regularity spaces. This is in sharp contrast to integer-order linear elliptic differential equations in which the smoothness of their coeffi cients and right-hand sides(plus the smoothness the domain for multidimensional problems) ensure the smoothness of their true solutions [ 7]. Consequently, it is not clear what conditions should be imposed on the coeffi cients and right-hand sides of sFDEs to ensure the smoothness of their solutions, which were assumed in the proof of the optimal-order error estimates ( 3)of the f inite element methods to problem ( 1) in the energy norm. Even worse, the optimal-order error estimates ( 4) of the f inite element methods to problem ( 1) in the L2norm were proved via the Nitsche lifting technique or duality arguments, under the assumption that the true solutions to the dual problem of problem ( 1) have full regularity for each right-hand side function in L2. While the counterexamples in [ 13, 22, 23] showed that the assumption does not hold. In other words, the Nitsche-lifting-based optimal-order L2error estimates of the form ( 4) are inappropriate.

The variable-coeffi cient analogue of Galerkin weak formulation ( 2) may lose its coercivity. It was shown in [ 21] that the Galerkin weak formulation for a variable-diff usivity analogue of problem ( 1) with a variable diff usivity coeffi cient that has positive lower and upper bounds may lose its coercivity, and so the wellposedness of the problem cannot be guaranteed. In fact, it was shown in [ 25] that the f inite element methods may diverge in this case. One may need to impose certain constraint on the magnitude of the diff usivity coeffi -cient to obtain the coercivity of the Galerkin weak formulation [ 10]. This is, again, in sharp contrast to integer-order linear elliptic differential equations, in which a variable-coeffi cient analogue of the homogeneous Dirichlet boundary-value problem of the Poisson equation is well posed. Moreover, their f inite element approximations are guaranteed to converge with an optimal-order convergence rate.

Inhomogeneous Dirichlet boundary-value problems of linear elliptic sFDEs. In the context of the homogeneous Dirichlet boundary condition, the sFDE ( 1), which is in the conservative Caputo form, coincides with the sFDE in the Riemann-Liouville form [ 5].However, the sFDEs in these two forms do not coincide in the context of inhomogeneous Dirichlet boundary conditions. In fact, it was shown in [ 23] that the inhomogeneous Dirichlet boundary-value analogue of problem ( 1) is well posed, but the inhomogeneous Dirichlet boundary-value problem of the sFDE in the Riemann-Liouville form has no weak solution.

Extensive research activities have been carried out on the numerical approximations and associated mathematical analysis of sFDEs. Here, we brief ly outline some of the recent developments.

A Petrov-Galerkin weak formulation for variable-coeffi cient sFDEs. A Petrov-Galerkin weak formulation was derived for the homogeneous Dirichlet boundary-value problem of the one-sided linear sFDE with a variable diff usivity coeffi cient, in which the weak formulation was proved to be weakly coercive that ensures the wellposedness of the weak formulation [ 21]. A Petrov-Galerkin f inite element method was developed for the problem subsequently [ 24]. Petrov-Galerkin formulations were developed for one-sided constantcoeffi cient sFDEs, in which the closed form analytical solutions were utilized to analyze the wellposedness of sFDEs [ 13].

Indirect f inite element methods and spectral Galerkin methods for the inhomogeneous Dirichlet boundary-value problems of one-sided variable-coeffi cient sFDEs. Based on the results in [ 21], indirect f inite element methods and spectral Galerkin methods were developed in [ 25] and [ 22], respectively, for the inhomogeneous Dirichlet boundary-value problems of the one-sided variable-coeffi cient sFDEs. This approach can be summarized as follows: (i) the true solutions to the inhomogeneous Dirichlet boundary-value problems of the one-sided variable-coeffi cient sFDEs are expressed in terms of the fractional diff erentiation of the solutions to integer-order differential equations, (ii) solve the integer-order differential equations to obtain their numerical approximations (e.g., f inite element solutions or spectral Galerkin solutions), and (iii) obtain the indirect numerical (e.g., f inite element or spectral) solutions by postprocessing the corresponding numerical solutions of the integer-order differential equations using the formulation derived in (i).

The key advantage of the indirect approach is as follows. In this approach, the smoothness of coeffi cients and source terms of the second-order differential equations ensure the smoothness of the solutions to the second-order equations, which ensures the high-order convergence rates of the corresponding f inite element methods and spectral Galerkin methods. Subsequently, the indirect solutions to the sFDEs, which are obtained by postprocessing the numerical solutions to the integer-order differential equations by the formulation derived in (i) retain high-order convergence rates to the true solutions to the sFDEs in the standard (not weighted) L2norm, under the regularity assumptions of the coeffi cients and source terms (but not the regularity of the true solutions). These results were proved mathematically and justif ied numerically in [ 22, 25].

Spectral and spectral Galerkin methods for sFDEs. Spectral and spectral Galerkin methods provide an alternative potential approach in the numerical approximations of sFDEs.Some related works were conducted under the fully regularity assumptions of the solutions to the models; see, e.g., [ 11, 26]. In [ 15], a spectral Galerkin method using Jacobi polynomials (cf [ 8, 20]) was developed for a two-sided variable-coeffi cient sFDE in which the regularity of the solutions was assumed to belong to some weighted Sobolev spaces in the convergence analysis.

The regularity of solutions to model ( 1) was thoroughly studied by Ervin et al. [ 6], in which, by means of weighted Jacobi spectral expansions, the solutions were proved to have a boundary layer in the form (1-x)α-βxβfor some α-1≤β≤1 determined by α and r.Based on the regularity results, rigorous analysis for both the f inite element approximations and spectral methods were conducted and (sub-) optimal-order convergence estimates of the error were derived in L2and Hα∕2norms and in weighted L2norms, respectively. A Petrov-Galerkin method for model ( 1) was then studied in [ 14] with the (two-sided) Jacobi polyfractonomials as basis and test functions and the corresponding error estimates were derived in proper weighted Sobolev spaces with the exponential decay rate. In [ 27], the regularity of the fractional Laplacian diff usion-reaction equations with constant coeffi cients was analyzed in weighted Sobolev spaces, based on which the sub-optimal convergence rates of the Jacobi spectral Galerkin method were proved in the weighted L2norms. The proposed methods were further extended to the fractional Laplacian advection-diff usion-reaction equations with constant diff usivity coeffi cients [ 9], in which the optimal-order convergence rates of the spectral Galerkin method were proved in both the weighted L2and Hα∕2norms.

In this paper, we study an indirect f inite element approximations for the variable-coeffi cient two-sided fractional diff usion equations. A key ingredient is to utilize the relation ( 11) between the solutions to the variable-constant model and that of the constant-coeffi cient analogues ( 1).Then after solving the constant-coeffi cient problems by the well-developed methods in references, we can obtain the approximations of the solutions to the variable-coeffi cient fractional diff usion equations by postprocessing. The advantages of the proposed indirect method are listed as follows: (i) by the relation ( 11), we only need to work on the constant-coeffi cient analogues of the variable-coeffi cient fractional diff usion equations, the numerical approximations of which have been extensively investigated and analyzed so the developed results can be directly applied in the analysis of the proposed method; (ii) as the main task of the proposed method is to solve the constant coeffi cient fractional diff usion equations, the Galerkin weak formulation of which is naturally coercive, we avoid any artif icial assumption on the data and the numerical divergence; (iii) in the case of f inite element methods, we use the convergence estimates of the approximations for the constant-coeffi cient models (cf. [ 6]) to prove that of the approximations for the variable-coeffi cient models in L2and Hα∕2norms with the optimalorder rather than in the weighted Sobolev norms; (iv) the representation ( 11) can be extended to accommodate the inhomogeneous boundary conditions of the variable-coeffi cient models(cf. [ 24]), based on which we are allowed to approximate the solutions to inhomogeneous boundary value problems with variable coeffi cients by only solving the constant-coeffi cient analogues with homogeneous boundary conditions.

The rest of the paper is organized as follows: in Sect. 2, we present the formulation of the model and introduce notations and key lemmas used in the analysis. The representation of the solutions u( x) to the proposed variable-coeffi cient model is presented in Sect. 3, based on which a f inite element approximation for the solutions v( x) to the constant-coeffi cient analogues is introduced and the approximations uh(x) of u( x) is obtained by plugging vh(x) , the approximation of v( x), into the representation of u( x). Optimal-order convergence analysis of u(x)-uh(x) is proved based on that of v(x)-vh(x) . Several numerical experiments are presented in Sect. 4 to demonstrate the sharpness of the derived error estimates and some concluding remarks are referred in the last section.

2 Problem Formulation and Preliminaries

We consider the following space-fractional diff usion equations for 1＜α＜2 [ 2, 28]:

where K( x) is the diff usivity coeffi cient with 0＜Km≤K(x)≤KM≤∞ , 0≤r≤1 and f( x)is the source or sink term. For m∈ℕ+and 0＜σ＜1 , the left and right Riemann-Liouville fractional derivatives of order m-σ are def ined by [ 18, 19]

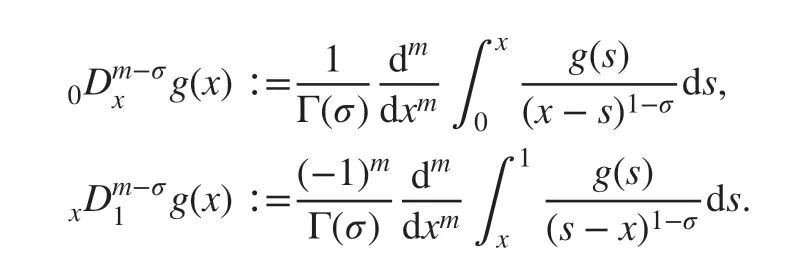
Let C∞(0,1) denote the space of continuous, inf initely diff erentiable, functions on the interval (0, 1), and(0,1) be the functions in C∞(0,1) that have compact support within(0, 1). Def ine the weighted L2space,(0,1) , and L2weighted inner product for any nonnegative integrable function ω(x) on x∈(0,1) as

In particular, if ω≡1 , the space and the inner product in ( 7) degenerate to the standard L2space equipped with the norm ‖·‖∶=‖·‖L2ω(0,1)and the L2inner product, respectively.Another important weight function takes the form of

which could properly characterize the boundary layer of the solutions to the fractional diffusion equations. We also denote L∞(0,1) by the space of essentially bounded functions;see [ 1].

Following [ 5], for μ＞0 def ine the semi-norm |g|JμL(0,1), and norm ‖g‖JμL(0,1)as

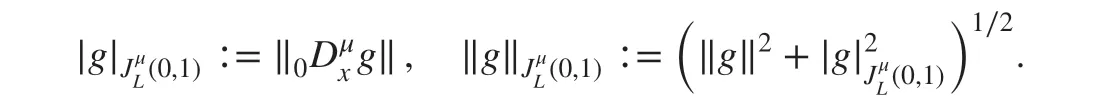
The left fractional derivative space(0,1) is then def ined as the closure of(0,1) with respect to

For 0＜μ＜1 , def ine the (Slobodetskii) semi-norm [ 3]:

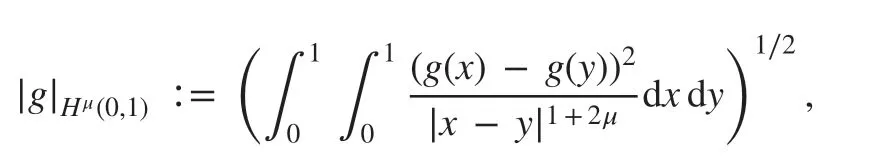
and for m-1＜σ＜m , m∈ℕ+the norm

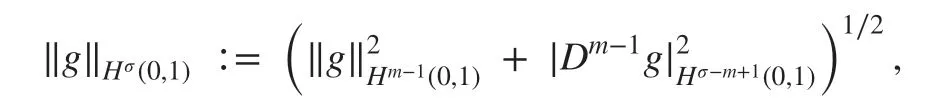
and let the fractional Sobolev spaces(0,1) denote the closure of(0,1) with respect to ‖·‖Hσ(0,1). We also def ine(0,1) the set of functions in Hσ(0,1) whose extension by 0 is in Hσ(ℝ).

Based on these def initions, we introduce the following lemmas.

Lemma 1[ 5] For 1 ∕2＜μ＜1 , the spaces(0,1) and(0,1) are equal with equivalent norms and semi-norms.

Lemma 2[ 5] For μ≥0 and g∈(0,1) , there exists a constant C＞0 such that

Lemma 3[ 17] Suppose 0＜μ＜1 and φ(x) is Lipschitz continuous on x∈[0,1] . Then,there exists a constant C＞0 such that

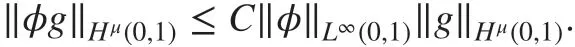
We f inally introduce the Gauss three-parameter hypergeometric function2F1(a,b;c,x)def ined by a series as follows:

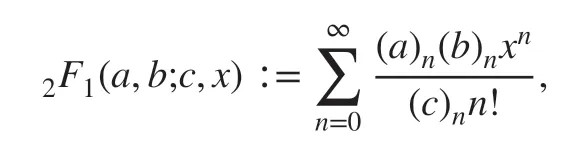
where (s)nis the rising Pochhammer symbol def ined by (s)n=Γ(s+n)∕Γ(s) . Some properties of2F1(a,b;c,x) are presented in the following lemma [ 19].

Lemma 4The Gauss three-parameter hypergeometric function2F1(a,b;c,x) is absolutely convergent for |x|＜1 and for |x|=1 if Re(c-a-b)＞0 . When Re(c)＞Re(b)＞0 , it has an integral representation

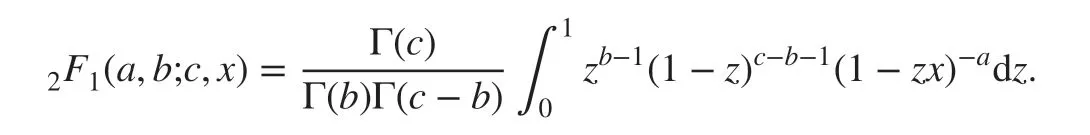
Furthermore, it satisf ies the Euler transformation formula

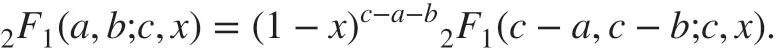
Remark 1Throughout, we use C to denote a generic positive constant whose actual value may change from line to line in the analysis.

3 Representation of the Solution u( x) and Its Finite Element Approximations

Let v( x) solve ( 5)-( 6) with K(x)≡1 , i.e., v( x) satisf ies

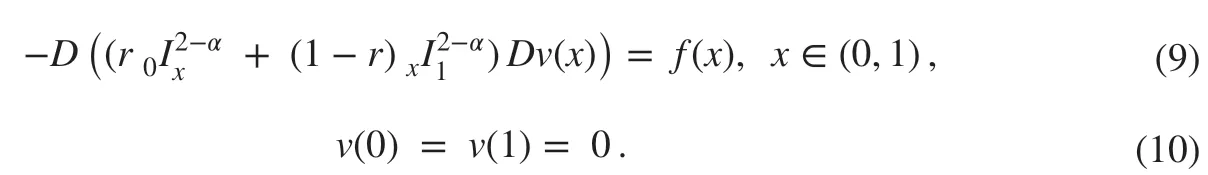
Next, let u( x) be def ined by

where ω(α-β-1,β-1)(x) is def ined by ( 8), α-1≤α-β,β≤1 and β is determined by

By construction, u(0)=u(1)=0 . From ( 11), ( 9), and the fact that ω(α-β-1,β-1)(x) is a kernel function of the operator -D(+(1-r)) [ 6], we obtain

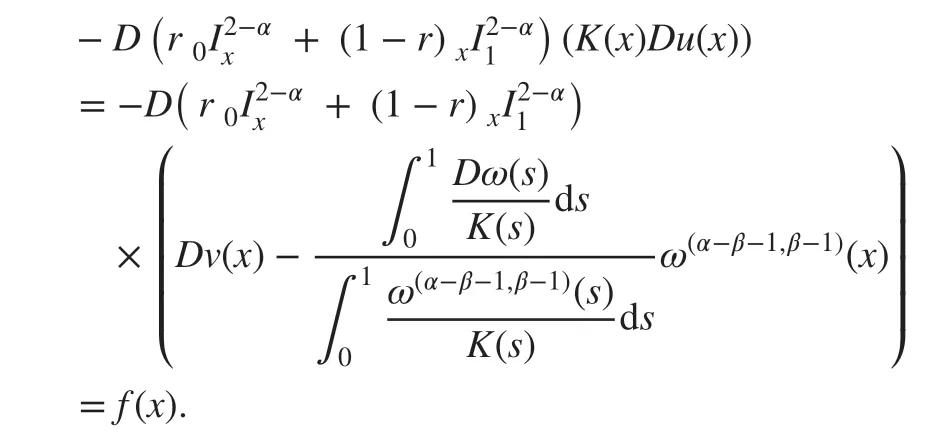
Therefore, we conclude that u( x) def ined by ( 11) is a solution of ( 5)-( 6), which motivates us to investigate the solution v( x) of ( 9)-( 10), and then obtain u( x) by ( 11). We refer the wellposedness of both the model ( 5)-( 6) and model ( 9)-( 10) in the following theorem.

Theorem1 [ 12] Let f(x)∈(0,1) . Then, model ( 9)-( 10) has a unique solution v(x)∈2(0,1) . In addition, there exists C＞0 such that

Furthermore, there exists a unique solution u(x)∈L∞(0,1) to ( 5)-( 6), given by ( 11).

Additionally, for ε1,ε2＞0 there exists C＞0 such that

3.1 Finite Element Approximations to u( x)

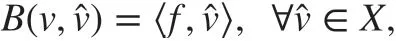
where B(·,·) is def ined by ( 2) and 〈·,·〉 denotes the L2duality pairing between H-α∕2(0,1)and

For 0=x0＜x1＜…＜xN=1 denoting a quasi-uniform partition of (0, 1), Xh⊂X denoting the space of continuous, piecewise polynomials of degree ≤1 on the partition, the f inite element approximation vh∈Xhto v is given by

From [ 6], the following error estimates of v-vhhold for any 0＜ε≪1:

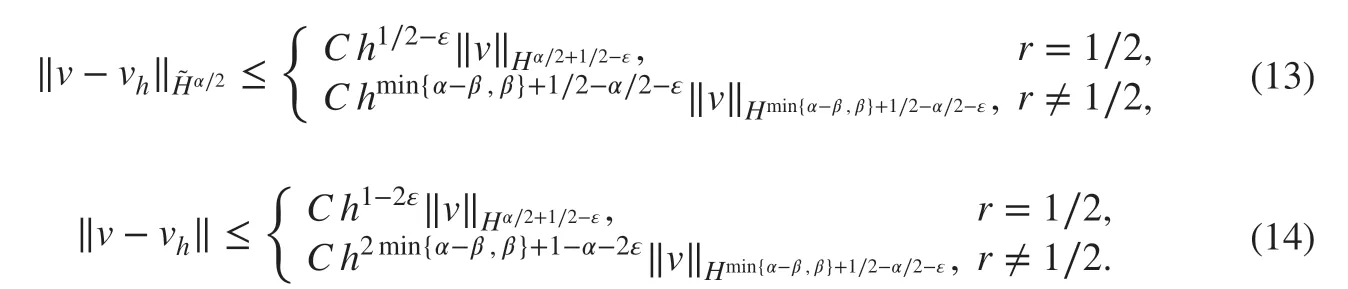
Using ( 11), the approximation uh(x) of u( x) is

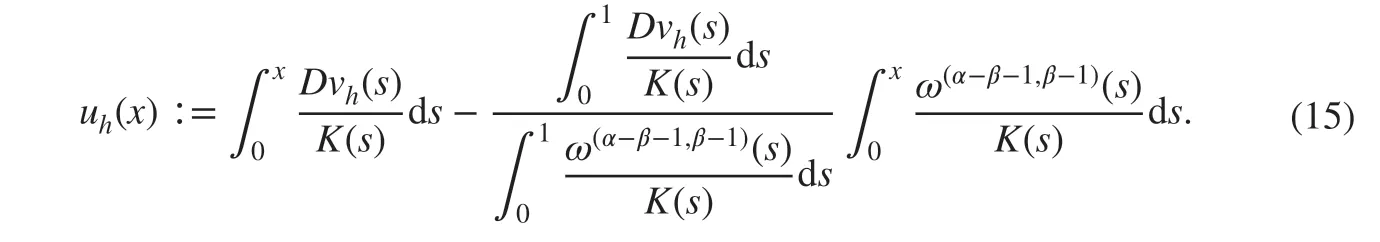
3.2 Convergence Estimates

We f irst prove the following lemma used in the convergence estimates of the f inite element approximations.

Lemma 5Let 1＜α＜2 , 0≤r≤1 and β be determined by ( 12). Then,

ProofWe f irst consider the case r≠1∕2 , which implies β≠α∕2 by ( 12). A direct calculation yields

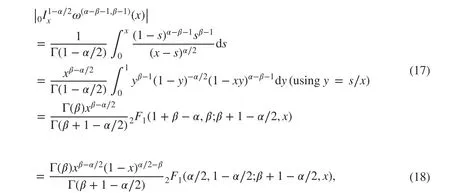
where we used the Euler transformation formula (Lemma 4) in the last step. Also, from Lemma 4, we have that the hypergeometric functions in ( 17) and ( 18) are absolutely convergent on x∈[0,1).

For β＜α∕2 , using Lemma 4 and the condition Re(c-a-b)＞0 , i.e.,β+1-α∕2-(1+β-α)-β=α∕2-β＞0 the hypergeometric function in ( 17) is absolutely convergent at x=1 , and hence on [0, 1]. Thus, it follows that hypergeometric function in ( 17) is bounded on [0, 1]. Also, as (β-α∕2)≥(α-1-α∕2)=α∕2-1＞-1∕2 ,then from ( 17) it follows that

For β＞α∕2 , using ( 18) it follows similarly thatFinally, for the case r=1∕2 , the relation ( 12) implies β=α∕2 . A direct calculation yields

As 1+σ-(1-α∕2)-α∕2=σ＞0 , we apply a similar argument as above to f inish the proof.

The error estimates of u-uhare given by the following theorem.

Theorem 2Suppose K(x)∈C1[0,1] . Then,

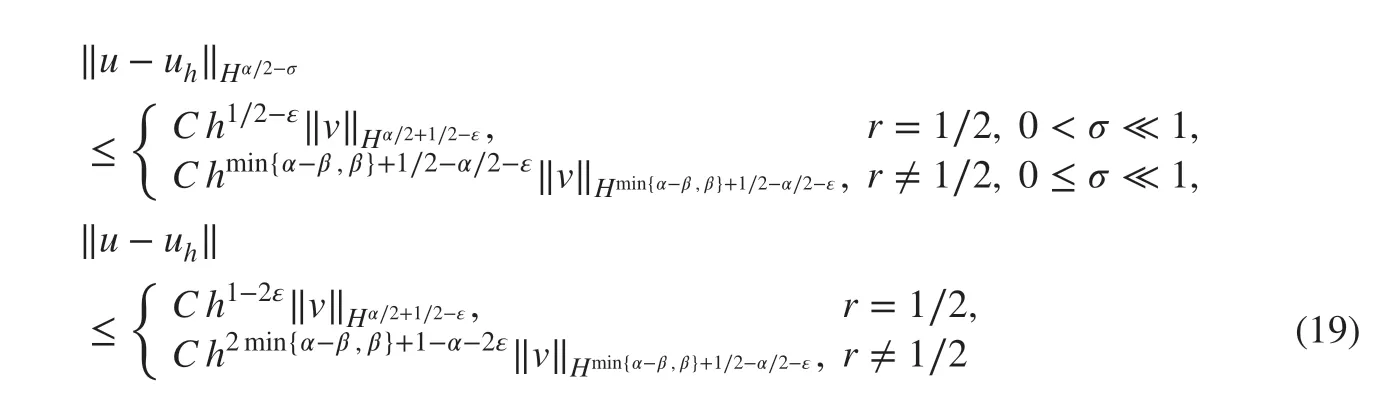
for any 0＜ε≪1.

ProofLet eu∶=u-uhand ev∶=v-vh. We subtract ( 11) from ( 15) to obtain

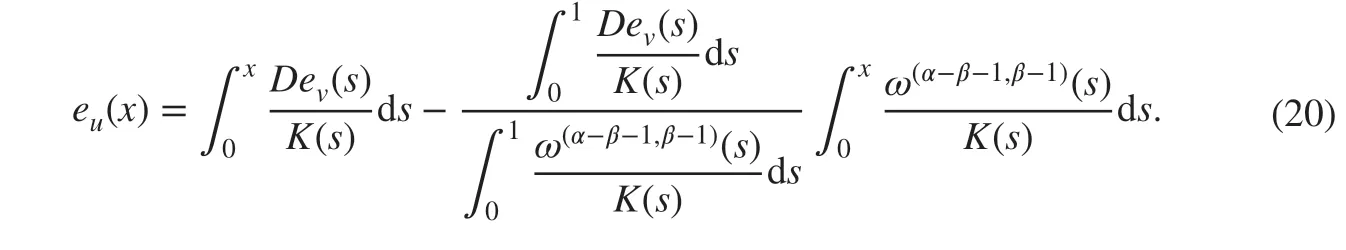
Using the integration by parts and the homogeneous boundary conditions of ev(x) , ( 20) can be rewritten as

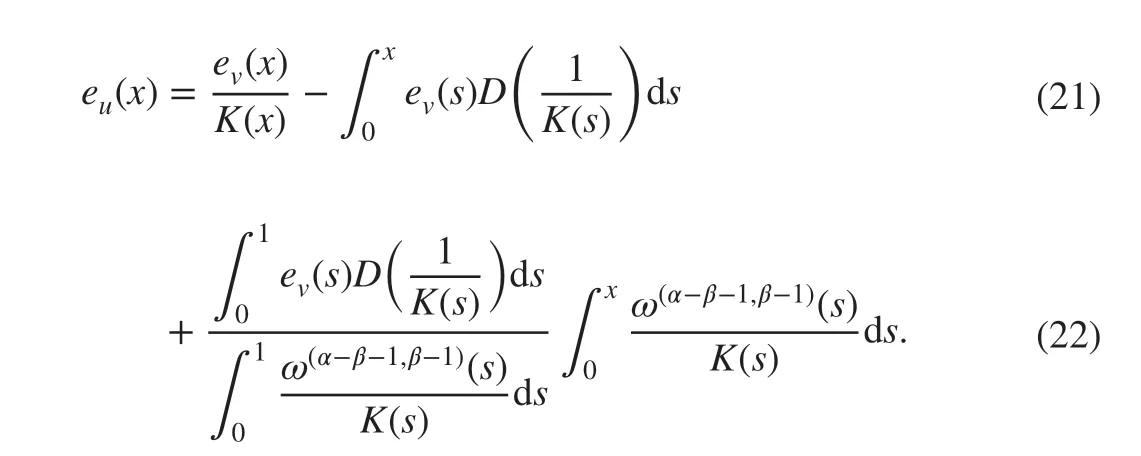
Taking the L2norm of both sides of ( 21), we obtain in which we have used the boundedness of D(1 / K( x)) derived based on K(x)∈C1[0,1] as follows:

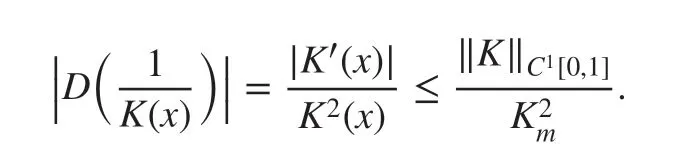
Then, an application of ( 14) leads to ( 19).

We turn to prove the estimate of ‖u-uh‖Hα∕2. We f irstly consider the case r≠0.5 .Applying the operatorto both sides of ( 20), we obtain

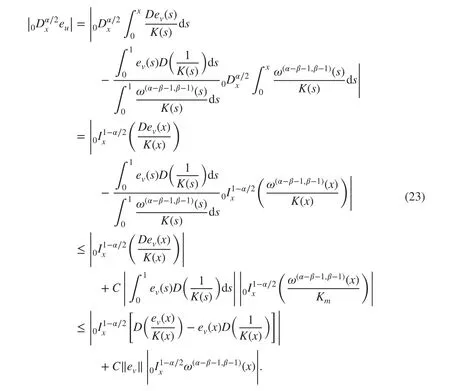
Taking the L2norm of both sides of ( 23) and using Lemmas 1, 3, 5, and that K∈C1[0,1] ,we obtain

Then, an application of Lemma 2 and ( 13) yields the error estimate of u-uhunder the norm ‖·‖Hα∕2for the case r≠0.5.

For r=0.5 , we follow exactly the same procedure as above where we applyon both sides of ( 20) instead offor any 0＜σ≪1 to derive the error estimate of u-uhunder the norm ‖·‖Hα∕2-σ.

4 Numerical Experiments

In this section, we present some numerical examples to support the error analysis (see Tables 1, 2, 3, 4, 5, 6, 7, 8 and Figs. 1, 2). We observe that for r≠1∕2 , the numerical results are in strong agreement with the error estimates proved in Theorem 2. For the case r=1∕2 , the estimate of ‖u-uh‖Hα∕2-σfor any 0＜σ≪1 was proved in Theorem 2 while we measured ‖u-uh‖Hα∕2in numerical experiments as it seems that the requirement of σ＞0 is caused by the limitation of analysis techniques and is not consistent with the estimates of v-vhin ( 13), ( 14). Numerical experiments show that the Hα∕2norm of u-uhconverges for r=1∕2 with the same convergence rate as ‖u-uh‖Hα∕2-σproved in Theorem 2, which numerically justif ies the proceeding discussions. Further study is needed to improve this estimate.

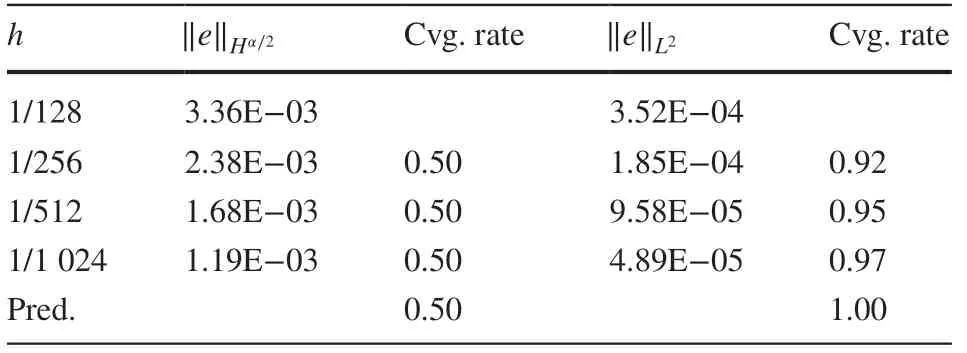
Table 1 Convergence rates for Experiment 1 when α=1.6 ,β=0.8 and r=0.5

Table 2 Convergence rates for Experiment 1 when α=1.6 ,β=0.9 and r=0.2764

Table 3 Convergence rates for Experiment 1 when α=1.2 ,β=0.6 and r=0.5

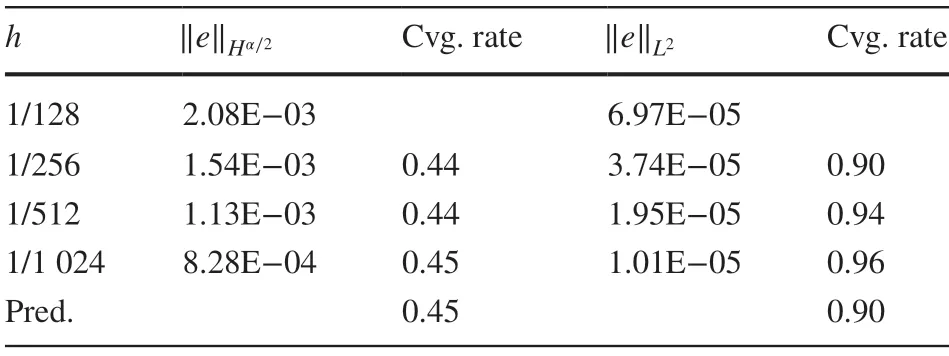
Table 4 Convergence rates for Experiment 1 when α=1.8 ,β=0.95 and r=0.2563

Table 5 Convergence rates for Experiment 2 when α=1.4 ,β=0.7 and r=0.5

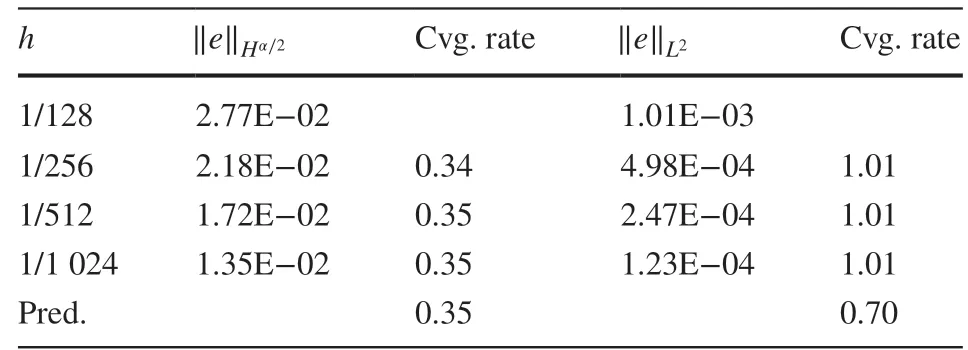
Table 6 Convergence rates for Experiment 2 when α=1.4 ,β=0.85 and r=0.3149

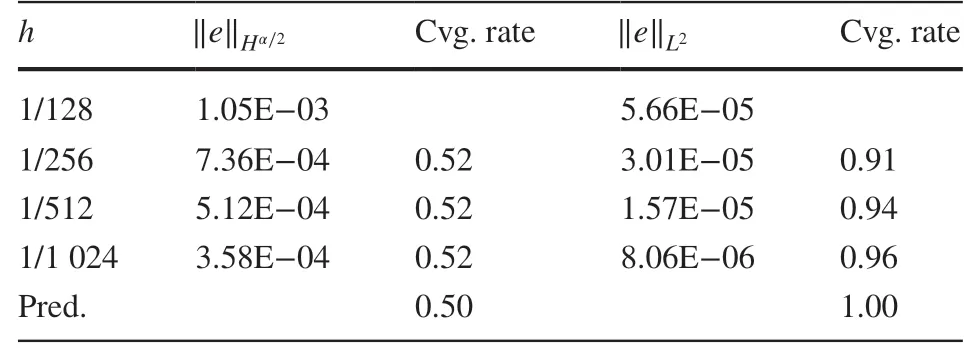
Table 7 Convergence rates for Experiment 2 when α=1.8 ,β=0.9 and r=0.5

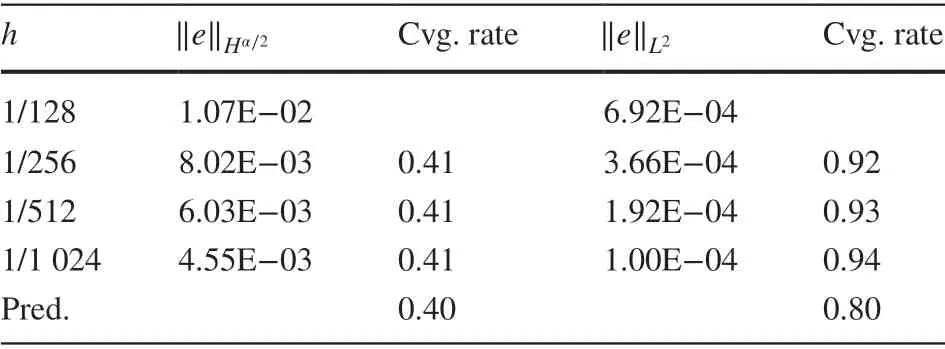
Table 8 Convergence rates for Experiment 2 when α=1.2 ,β=0.5 and r=0.5528

Fig. 1 Plots of true solution u( x)and numerical solution uh(x)for Experiment 1 with α=1.6 ,β=0.9 and r=0.2764

Fig. 2 Plots of true solution u( x)and numerical solution uh(x)for Experiment 2 with α=1.8 ,β=0.9 and r=0.5

Experiment 1Let K(x)=1∕(1+x) and β be determined by ( 12). For the right-hand side term in ( 5) given by

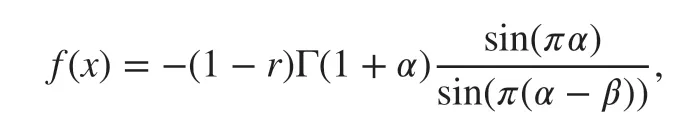
the solution u( x) is given by ( 11) where v(x)=(1-x)α-βxβ(Figs. 1, 2).

Experiment 2Let K(x)=1∕(1+x) and β be determined by ( 12). For the right-hand side term in ( 5) given by

the solution u( x) is given by ( 11) where

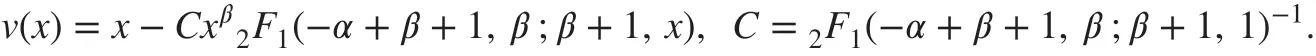
5 Concluding Remarks

In this paper, we established an indirect f inite element approximation for the two-sided space-fractional diff usion equations in one space dimension. By the representation of the solutions u( x) to the proposed variable coeffi cient model in terms of v( x), the solutions to the constant coeffi cient analogues, we apply f inite element methods for the constant coeffi cient fractional diff usion equations to solve for the approximations vh(x) to v( x) and then obtain the approximations uh(x) of u( x) by plugging vh(x) into the representation of u( x). We also proved the optimal-order convergence estimates of u(x)-uh(x) in L2and Hα∕2norms by those of v(x)-vh(x) proved in [ 5]. Numerical results are in agreement with the derived theoretical estimates.If the solutions u( x) to model ( 5)-( 6) have inhomogeneous boundary conditions,i.e., u(0)=a and u(1)=b , the representation ( 11) can be modif ied to accommodate the impact

where v( x) is still the solutions to ( 9), ( 10). All the derivations in this paper can be extended to this case without any diffi culty. Other developed methods for the constant-coeffi cient fractional diff usion equations, which can recover the convergence rates of the numerical approximations, can also be applied to the variable-coeffi cient models by the relation ( 24)and we will carry on these studies in the near future.

AcknowledgementsThis work was funded by the OSD/ARO MURI Grant W911NF-15-1-0562 and by the National Science Foundation under Grant DMS-1620194.

Compliance with ethical standards

Conf lict of interestOn behalf of all authors, the corresponding author states that there is no conf lict of interest.