Finite Element Convergence for State-Based Peridynamic Fracture Models

Prashant K. Jha · Robert Lipton

Abstract We establish the a priori convergence rate for f inite element approximations of a class of nonlocal nonlinear fracture models. We consider state-based peridynamic models where the force at a material point is due to both the strain between two points and the change in volume inside the domain of the nonlocal interaction. The pairwise interactions between points are mediated by a bond potential of multi-well type while multi-point interactions are associated with the volume change mediated by a hydrostatic strain potential. The hydrostatic potential can either be a quadratic function, delivering a linear force-strain relation, or a multi-well type that can be associated with the material degradation and cavitation. We f irst show the well-posedness of the peridynamic formulation and that peridynamic evolutions exist in the Sobolev space H2 . We show that the f inite element approximations converge to the H 2 solutions uniformly as measured in the mean square norm.For linear continuous f inite elements, the convergence rate is shown to be C tΔt+Csh2∕ε2 ,where ε is the size of the horizon, h is the mesh size, and Δ t is the size of the time step. The constants C t and C s are independent of Δ t and h and may depend on ε through the norm of the exact solution. We demonstrate the stability of the semi-discrete approximation. The stability of the fully discrete approximation is shown for the linearized peridynamic force.We present numerical simulations with the dynamic crack propagation that support the theoretical convergence rate.

Keywords Nonlocal fracture models · Peridynamic · State-based peridynamic · Numerical analysis · Finite element approximation

1 Introduction

In this work, we study the state-based peridynamic theory and obtain an a priori error bound for the f inite element approximation. The peridynamic theory is a reformulation of classical continuum mechanics carried out in the work of Silling in [ 34, 37]. The strain inside the medium is expressed in terms of displacement differences as opposed to the displacement gradients. Acceleration of a point is now due to the sum of the forces acting on the point from nearby points. The new kinematics bypasses the diffi culty incurred by juxtaposing displacement gradients and discontinuities as in the case of classical fracture theories. The nonlocal fracture theory has been applied numerically to model the complex fracture phenomenon in materials; see [ 1, 3, 11, 15, 17, 19, 27, 35, 36, 38, 40]. Every point interacts with its neighbors inside a ball of f ixed radius is called the horizon. The size of the horizon sets the length scale of the nonlocal interaction. When the forces between points are linear and the nonlocal length scale tends to zero, it is seen that peridynamic models converge to the classic model of the linear elasticity; see [ 2, 14, 32, 36]. The work of [ 39] provides an analytic framework for analyzing FEM for the linear bond and state-based peridynamics. For nonlinear forces associated with double well potentials, the peridynamic evolution converges in the small horizon limit to an evolution with a sharp evolving fracture set and the evolution is governed by the classic linear elastic wave equation away from the fracture set; see [ 21, 25, 26]. A recent review of the state of the art can be found in [ 4] and [ 9].

In this work, we assume small deformation and work with the linearized bond-strain. Let D⊂ℝd, for d=2,3 , be the material domain. For a displacement f ield u∶D×[0,T]→ℝd,the bond-strain between two material points x,y∈D is given by

Let ε＞0 be the size of the horizon and Hε(x)={y∈ℝd∶|y-x|＜ε} be the neighborhood of a material point x . For pairwise interaction, we assume the following form of pairwise interaction potential:

where Jε(|y-x|) is the inf luence function. We assume Jε(|y-x|)=J(|y-x|∕ε) where 0≤J(r)≤M for r＜1 and J(r)=0 for r≥1 . The potential f, see Fig. 1 a, is assumed to be convex for small strains and becomes concave for larger strains. In the widely used prototypical micro-elastic brittle (PMB) peridynamic material, the strain vs force prof ile is linear up to some critical strain Scand is zero for any strain above Sc. In contrast, the peridynamic force given by ∂SWεis linear near zero strain and as the strain gets larger and reaches the critical strain,for positive (negative) strain, the bond starts to soften,see Fig. 1 b. For a given potential function f, the critical strain is given byandwhere r+＞0,r-＜0 are the inf lection points of the potential function f as shown in Fig. 1 a.

The spherical or hydrostatic strain θ(x,t;u) at material point is given by

Fig. 1 a Potential function f( r) for tensile force. C+ and C- are two extreme values of f. b Cohesive tensile force

where ωdis the volume of the unit ball in dimension d=2,3 . The potential for hydrostatic interaction is of the form

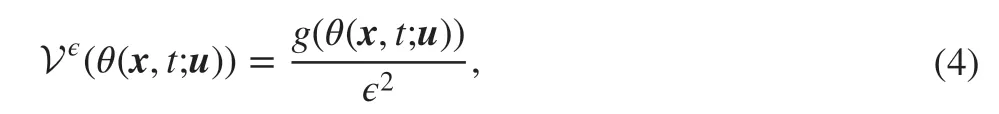
where g is the potential function associated with the hydrostatic strain. Here g can be of two types: (i) a quadratic function with only one well at zero strain, and (ii) a convex-concave function with a wells at the origin and at ±∞ ; see Fig. 2 a. If g is assumed to be quadratic, then the force due to the spherical strain is linear. If g is a multi-well potential, the material softens as the hydrostatic strains exceed the critical value. For the convex-concave type g, the critical values are 0＜and＜0 beyond which the force begins to soften is related to the inf lection pointandof g as follows:

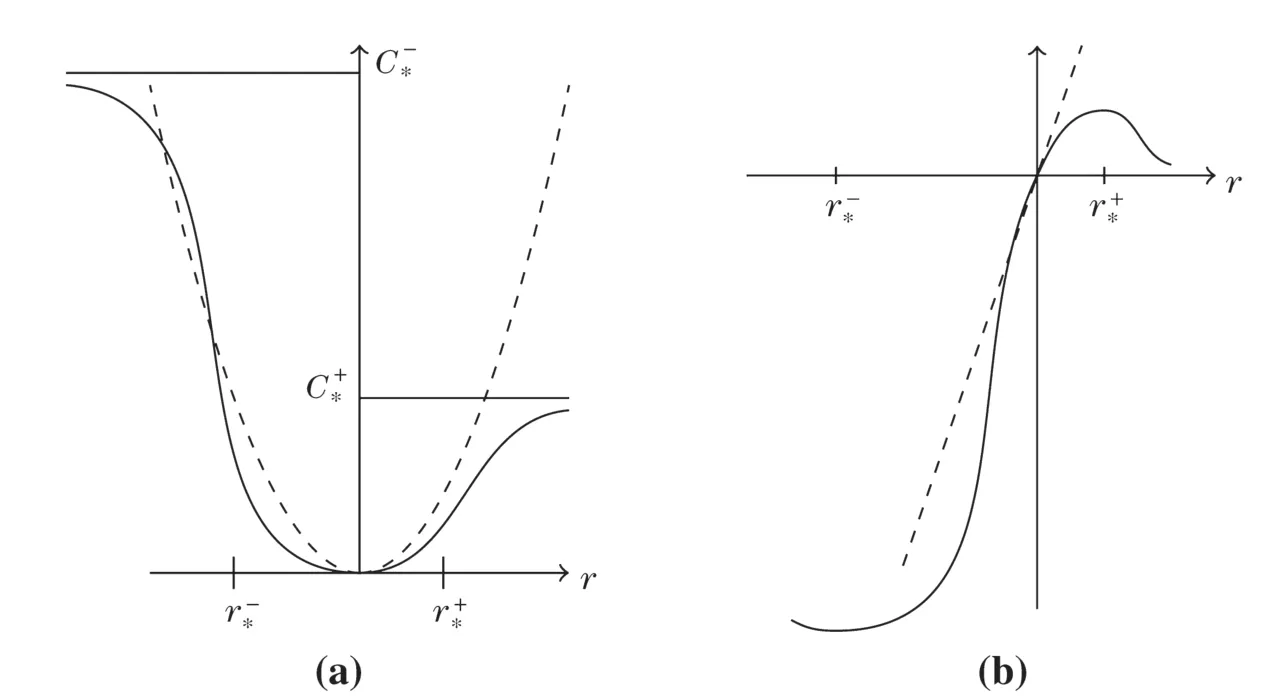
Fig. 2 a Two types of potential function g( r) for hydrostatic force. Dashed line corresponds to the quadratic potential g(r)=βr2∕2 . Solid line corresponds to the convex-concave type potential g( r). For the convexconcave type potential, there are two special points and at which material points start to soften. andare two extreme values. b Hydrostatic forces

The critical compressive hydrostatic strain where the force begins to soften for negative hydrostatic strain is chosen much larger in magnitude than, i.e.,＜＜.

The f inite element approximation has been applied to the peridynamic fracture;however, there remains a paucity of literature addressing the rigorous a priori convergence rate of the f inite element approximation to peridynamic problems in the presence of material failure. This aspect provides the motivation for the present work. In this paper, we f irst prove the existence of peridynamic evolutions taking values in H2(D;ℝd)∩(D;ℝd) that are twice diff erentiable in time; see Theorem 2. We note that as these evolutions will become more fracture like as the region of the nonlocal interaction decreases. These evolutions can be thought of as inner approximations to fracture evolutions. On passing to subsequences it is possible to show that the H2(D;ℝd)∩(D;ℝd) evolutions converge in the limit of vanishing non-locality to a limit solution taking values in the space of special functions of bounded deformation SBD. Here the limit evolution has a well-def ined Griffi th fracture energy bounded by the initial data; see [ 26] and [ 23]. We show here that the higher temporal regularity can be established if the body force changes smoothly in time. Motivated by these considerations, we develop f inite element error estimates for solutions that take values in H2(D;ℝd)∩(D;ℝd) and for a bounded time interval.

In this paper, we obtain an a priori L2error bound for the f inite element approximation of the displacement and velocity using a central in time discretization. Due to the nonlinear nature of the problem, we get a convergence rate using the Lax-Richtmyer stability together with the consistency. Both the stability and consistency are shown to follow from the Lipschitz continuity of the peridynamic force in L2(D;ℝd) ; see Sects. 4.2.1 and 4.2.2.The bound on the L2error is uniform in time and is given by CtΔt+Csh2∕ε2, where the constants Ctand Csare independent of Δt and the mesh size h; see Theorem 6. A more elaborate discussion of the a priori bound is presented in Sect. 4.2. For the linearized model, we obtain a stability condition on Δt , Theorem 9, that is of the same form as those given for linear local and nonlocal wave equations [ 18, 24]. We demonstrate the stability for the linearized model noting that for small strains the material behaves like a linear elastic material and that the stability of the linearized model is necessary for the stability of nonlinear model. We believe a more constructive CFL stability condition is possible for the linear case and will pursue this in future work.

Previous work [ 21] treated spatially Lipschitz continuous solutions and addressed the f inite difference approximation and obtained bounds on the L2error for the displacement and velocity that are uniform in time and of the form CtΔt+Csh∕ε2, where the constants Ctand Csare as before. For f inite elements, the convergence rate is seen to be slower than for the FEM model introduced here and is of order h∕ε2as opposed to h2∕ε2. On the other hand, the FEM method increases the computational work due to the inversion of the mass matrix.

We carry out numerical experiments for dynamic crack propagation and obtain convergence rates for Plexiglass that are in line with the theory; see Sect. 5. We also compare the Griffi th's fracture energy with the peridynamic energy of the material softening zone; we show good agreement between the two energies; see Sect. 5.2. Finite difference methods are less expensive than f inite element approximations for nonlocal problems; however, the latter off ers more control on the accuracy of solution; see [ 10, 13, 16, 30, 31].

Here the a priori L2convergence rates for the FEM given by Theorem 6 include the eff ects of material degradation through the softening of material properties. The FEM simulations presented in this paper show that the material develops localized softening zones (region where bonds exceed the critical tensile strain) as it deforms. This is in contrast to linear peridynamic models which are incapable of developing softening zones. For nonlinear peridynamic models with material failure, the localization of zones of softening and damage is the hallmark of the peridynamic modeling [ 15, 19, 34, 37]. One notes that the a priori error involves ε in the denominator and in many cases ε is chosen small.However, typical dynamic fracture experiments last only hundreds of microseconds and the a priori error is controlled by the product of simulation time multiplied by h2∕ε2. So for material properties characteristic of Plexiglass and ε of size 4 mm, the a priori estimates predict a relative error offor simulations lasting around 100 μ s. We point out that the a priori error estimates assume the appearance of nonlinearity anywhere in the computational domain. On the other hand, the numerical simulation and independent theoretical estimates show that the nonlinearity concentrates along “fat” cracks of f inite length and width equal to ε ; see [ 25, 26]. Moreover, the remainder of the computational domain is seen to behave linearly and to leading order can be modeled as a linear elastic material up to an error proportional to ε ; see [Proposition 6, [ 22]]. Future work will use these observations to focus on the adaptive implementation and a posteriori estimates. A posteriori convergence for FEM models of peridynamics with material degradation can be seen in the work [ 7, 31, 33]. For other nonlinear and nonlocal models, the adaptive mesh ref inement within FE framework for nonlocal models has been explored in [ 13] and convergence of the adaptive FE approximation is rigorously shown. A posteriori error analysis of linear nonlocal models is carried out in [ 12].

The paper is organized as follows. We introduce the equation of motion in Sect. 2 and present the Lipschitz continuity of the force, existence of peridynamic solution, and the higher temporal regularity necessary for the f inite element error analysis. In Sect. 3, we consider the f inite element discretization. We prove the stability of a semi-discrete approximation in Sect. 3.1. In Sect. 4, we analyze the fully discrete approximation and obtain an a priori bound on errors. The stability of the fully discrete approximation linearized peridynamic force is shown in Sect. 4.3. We present our numerical experiments in Sect. 5. Proofs of the Lipschitz bound on the peridynamic force and higher temporal regularity of solutions is provided in Sect. 6. In Sect. 7, we present our conclusions.

We conclude the introduction by listing the notation used throughout the paper. We denote material domain as D, where D⊂ℝdfor d=2,3 . Points and vectors in ℝdare denoted as bold letters. Some of the key notations are as follows:

[0, T] Time domain ε Size of horizon ρ Density Hε(x) Horizon of x∈D , a ball of radius ε centered at x ωd Volume of unit ball in dimension d=2,3 ω(x)∈[0,1] Boundary function def ined on D taking value 1 in the interior and smoothly decaying to 0 as x approaches ∂D u Displacement f ield def ined over D×[0,T] . We may also use notation u to denote f ield def ined over just D u0,v0 Initial condition on displacement b Body force def ined over D×[0,T]ey-x The unit vector pointing from a point y to the point x

S=S(y,x,t;u) Bond strain S=u(y,t)-u(x,t)|y-x| ·ey-x . We may also use S(y,x;u) if u is a f iled def ined over just D θ=θ(x,t;u) Spherical or hydrostatic strain. We may also use θ(x;u) if u is a f iled def ined over just D S+c,Sc Critical bond strain θ+c,θc Critical hydrostatic strain Jε(r)=J(r∕ε) Inf luence function where J is integrable with J(r)=0 for r≥1 and 0≤J(r)≤M for r＜1¯Jα Moment of function J over H1(