A Discontinuous Galerkin Method with Penalty for One-Dimensional Nonlocal Diff usion Problems

Qiang Du · Lili Ju · Jianfang Lu · Xiaochuan Tian

Abstract There have been many theoretical studies and numerical investigations of nonlocal diffusion (ND) problems in recent years. In this paper, we propose and analyze a new discontinuous Galerkin method for solving one-dimensional steady-state and time-dependent ND problems, based on a formulation that directly penalizes the jumps across the element interfaces in the nonlocal sense. We show that the proposed discontinuous Galerkin scheme is stable and convergent. Moreover, the local limit of such DG scheme recovers classical DG scheme for the corresponding local diff usion problem, which is a distinct feature of the new formulation and assures the asymptotic compatibility of the discretization. Numerical tests are also presented to demonstrate the eff ectiveness and the robustness of the proposed method.

Keywords Nonlocal diff usion · Discontinuous Galerkin method · Interior penalty ·Asymptotic compatibility · Strong stability preserving

1 Introduction

Recent development of nonlocal modeling has attracted much attention in many application f ields, ranging from solid mechanics and anomalous diff usion to imaging analysis and machine learning [ 12, 13, 20, 21, 28- 32]. One of major differences between the nonlocal models and the local models is that the nonlocal models are integral-type equations, while the classical local models are often involved with differential operators. As an example, the peridynamic model was f irstly introduced in [ 29] to study crack and fracture of materials, since the classical continuum models may not be eff ective when discontinuities occur. Nonlocal models can also be used to develop and study numerical schemes for local problems [ 17]. Indeed, nonlocal modeling can provide a new approach to describe both continuous and discontinuous phenomena in a unif ied mathematical model; it also off ers a tool and bridge to understand and connect existing models.

As generalizations of classical PDE-based models, many nonlocal models like the peridynamics and nonlocal diff usion (ND) models are characterized by a horizon parameter δ ,such that the nonlocal models would converge to the corresponding classical ones if the latter make sense as δ goes to zero. To introduce the nonlocal model under consideration in this paper, we recall that the ND operator Lδrepresented as follows:

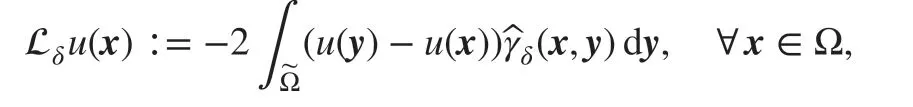
where Ω⊆ℝnis a bounded, open domain (note that we focus on the case n=1 in later sections), and ~Ω=Ω∪Ωδwith Ωδ⊆ℝnbeing of a nonzero volume that is not necessarily located near or at the boundary of Ω . The kernel function

is nonnegative and symmetric, i.e.,(x,y)=(y,x)≥0 . To connect with its local limit, we may make some extra assumptions (see [ 13, 26, 33]) thatare radial (i.e.,=γδ(|x-y|) ) and compactly supported in a ball Bδ(0) with bounded second-order moments def ined by

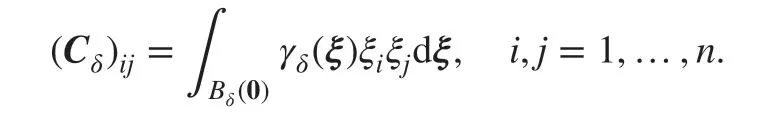
Then, we have Lδ→∇·(C·∇) as δ →0 , where C =is a second-order tensor. To preserve such mathematical property on the local limit in the discrete sense, a number of studies have been carried out to obtain the so-called asymptotically compatible schemes for solving nonlocal problems [ 33, 34]. In [ 33], Tian and Du pointed out that the solutions based on some numerical schemes would converge to the wrong local limits as the horizon goes to zero. They also showed numerical schemes that avoid such mishaps. Then, they further established in [ 34] an abstract mathematical framework to analyze a class of asymptotically compatible schemes for conforming Galerkin approximations of some parameterized linear nonlocal problems. Meanwhile, some numerical methods such as f inite difference, f inite element, Fourier spectral, and discontinuous Galerkin (DG) approaches have been designed and studied to satisfy the asymptotic compatibility (see, e.g., [ 14, 16, 18, 33,35]). When the kernel function γδis chosen such that the solution of the nonlocal diff usion problem contains spatial discontinuities, the DG method could be an advantageous choice for its discretization in space.

Since the major development in the 1990s [ 6- 10], the DG methods have been widely used in many areas such as aero-acoustics, viscoelastic f lows, electromagnetism, gas dynamics, and oceanography for their robustness and capability of handling discontinuities. Particularly, there exist various DG approximations for the classical elliptic problems(see, e.g., [ 1, 5, 24]). For the nonlocal diff usion and nonlocal mechanical models, diff erent conforming and nonconforming Galerkin approximations using discontinuous elements have been considered in [ 4, 19, 25, 27, 35]. The DG scheme recently proposed in [ 14] for solving the ND equation is motivated by the local discontinuous Galerkin (LDG) method[ 11] and relies on the introduction of auxiliary variables. In this paper, we propose a DG method with penalty technique for solving one-dimensional ND problems without introducing auxiliary variables. The method is applied to both steady-state and time-dependent ND problems. We prove the Poincaré's inequality at the discrete level and derive the stability, boundedness, a priori error estimates, and asymptotic compatibility of the proposed scheme. In fact, the local limit of the proposed DG scheme (as the horizon goes to zero) is shown to be identical to the one proposed by Babuška and Zlámal in [ 3] for the classical diff usion problems. In numerical experiments for the time-dependent ND problem, we use the singly diagonal implicit Runge-Kutta method (SDIRK) for time stepping, which is of strong stability based on the analysis done in [ 15].

The paper is organized as follows. In Sect. 2, we brief ly introduce the one-dimensional ND problem, including the steady-state and time-dependent ones. In Sect. 3, we present semi-discrete DG schemes for the ND problems, which directly penalize the jumps across element interfaces in the nonlocal sense. In Sect. 4, we f irst prove a Poincaré's inequality at the discrete level and then, we derive the stability, boundedness, and a priori error estimates of the DG scheme for steady-state ND problems. The error estimates imply that the DG scheme is asymptotically compatible. We also obtain the L2-stability and a priori error estimates of the DG scheme for the time-dependent ND problems. In Sect. 5, numerical examples are given to demonstrate the eff ectiveness and the robustness of the proposed DG method. Some concluding remarks are f inally given in Sect. 6.

2 The Model Problem

Let us consider a one-dimensional steady-state nonlocal diff usion problem with nonlocal volume constraints given as follows:

where δ＞0 is the horizon and fδ∈L2(Ω) , ~Ω=Ω∪Ωδ. The corresponding time-dependent problem of ( 1) is given by

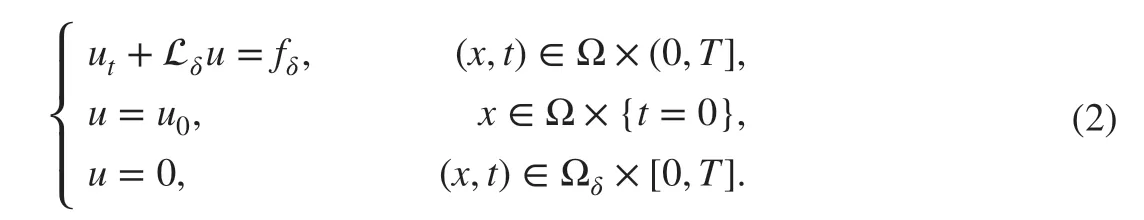
The nonlocal diff usion operator Lδis def ined as

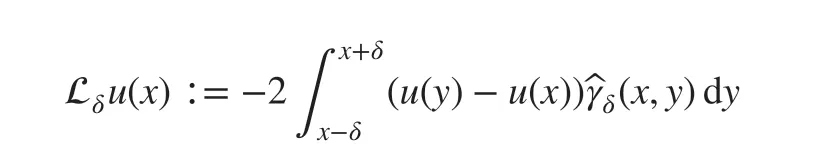
The solution space associated with ( 1) is

where the energy norm ‖u‖Lis def ined as

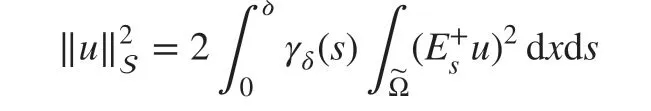
and

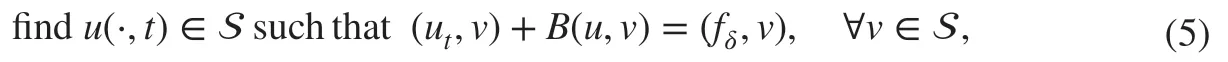
where (·,·) is the L2inner product and

Since s2γδ(s)∈(ℝ) , we have

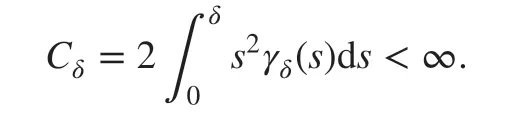
To connect with the local limit, without loss of generality, it is assumed that

which can always be achieved by a rescaling of γδ(s).

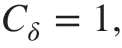
Thus, when δ→0 , the nonlocal diff usion operator becomes the classical (local) diff usion operator, which implies that ( 1) and ( 2) converge to the Poisson's equation and heat equation, respectively (see [ 13, 33] for more details).

3 Discontinuous Galerkin Approximations with Penalty

In this section, we propose a new DG method which directly imposes penalties on the jumps across element interfaces instead of introducing auxiliary variables as done in [ 14]for discretizing the problems ( 1) and ( 2).

First, we take the partition of the domainaswith

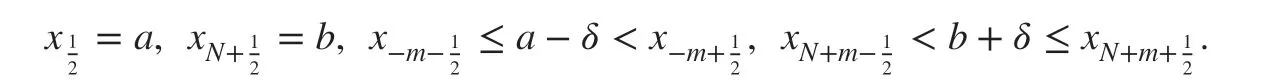
Now, we def ine a f inite element space Vhas

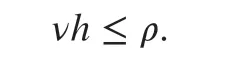
where Pk(Ij) is the space of polynomials on Ijwhose degrees are at most k.

Let us rewrite the bilinear form B( u, v) in ( 6) as follows:

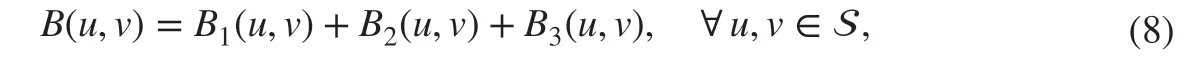
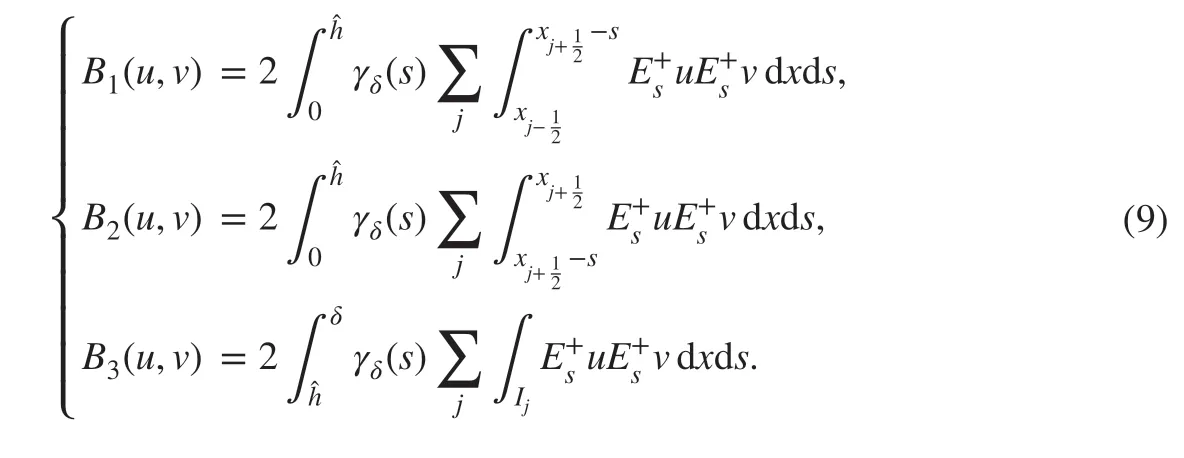
We are interested in modifying B( u, v) so that it may be def ined in the discrete spaces. For uhand vhin Vh, one can see f irst that B1(uh,vh) and B3(uh,vh) in the RHS of ( 8) can be well def ined but B2(uh,vh) could become problematic if uhand vhare discontinuous at the element interfaces. In fact, if we f ix hj, we have formally that

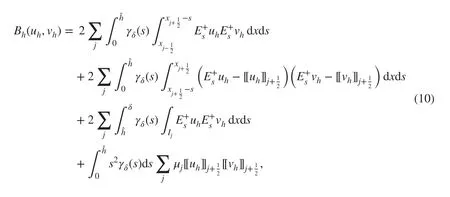
where the penalty parameters {μj＞0} are expected to be suffi ciently large for deriving the error estimates later on. In particular, with μj=O(h-2k-1) , we are able to recover the DG scheme designed by Babuška and Zlámal [ 3] in the local zero horizon limit.

To see the local limit more clearly, let us f ix hj. As δ→0 , we have

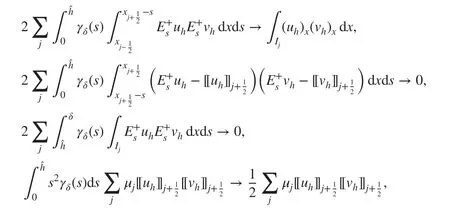
which correspond to the original DG scheme proposed in [ 3]. It is known in the literature that this superpenalty procedure makes the DG method behave like a standard conforming method and increases the condition number of the stiff ness matrix signif icantly [ 1].

We now present the new DG scheme with penalty for the problem ( 1) as follows:

The corresponding semi-discrete DG scheme for solving the time-dependent problem ( 2)is given by:

where the initial uh(x,0)∈Vhis taken as the standard L2projection of u0onto Vh.

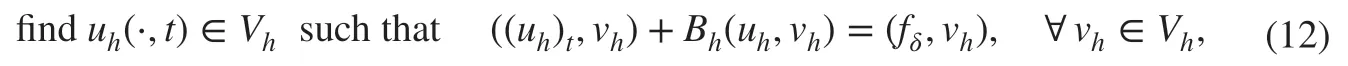
4 Stability, Boundedness, and a Priori Error Estimates

In this section, we f irst present the discrete Poincaré's inequality and then study the boundedness and stability results of ( 11), which enable us to derive a priori error estimates. Next,we prove the L2-stability and a priori error estimates of the semi-discrete DG scheme ( 12).Throughout this section, we let C＞0 represent a generic positive constant independent of h and δ with possibly diff erent values if not noted otherwise. Let us def ine the semi-norms for v∈Vhas follows:

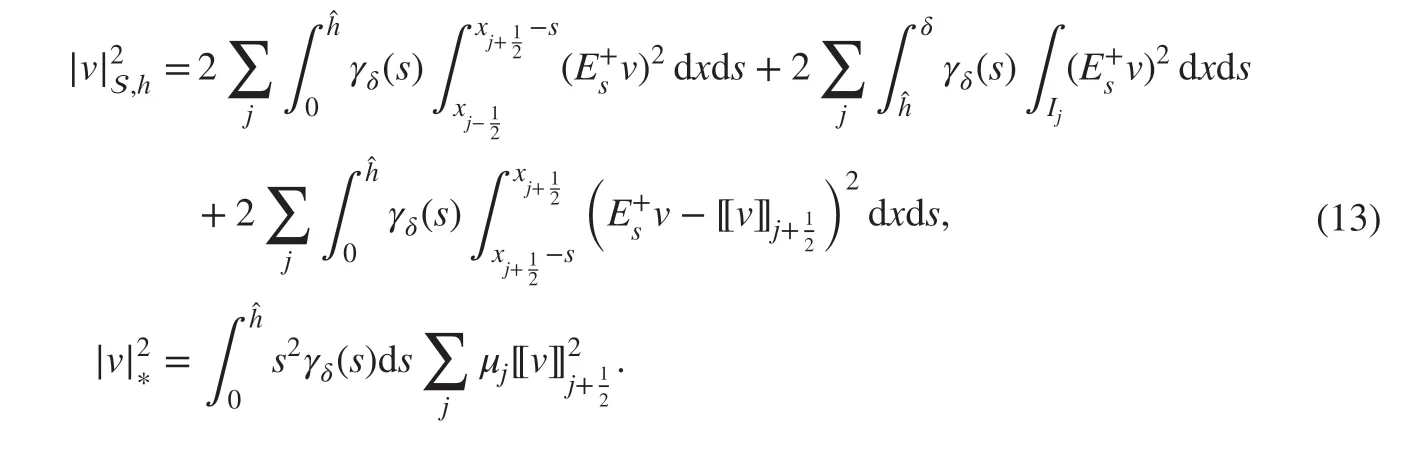
By the def inition of the bilinear form ( 10) and the semi-norms ( 13), we immediately have

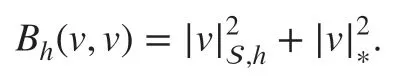
Then, we def ine the semi-norm

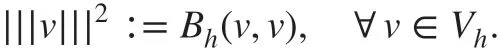
4.1 Discrete Poincaré's Inequality

To ensure that |||·||| is a norm on Vh, we need to derive some Poincaré's inequalities at the discrete level. First, let us present the result when the kernel γδis bounded on [0,δ].

Lemma 4.1For a bounded γδ, it holds that

where the constant C＞0 is independent of δ and h.

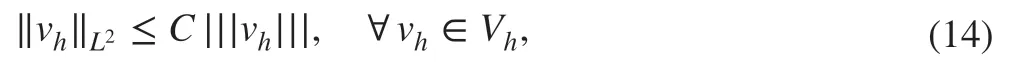
ProofFollowing [ 2], we consider the problem Lδφ=vhfor any vh∈Vhwith a bounded kernel γδ. Then, the energy space L is indeed the L2space and it is implied by the nonlocal Poincaré's inequality ([ 26]) that the following energy inequality holds:

where C＞0 is a constant independent of δ . For the DG scheme ( 11) and by the Cauchy-Schwarz inequality, we have

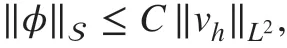
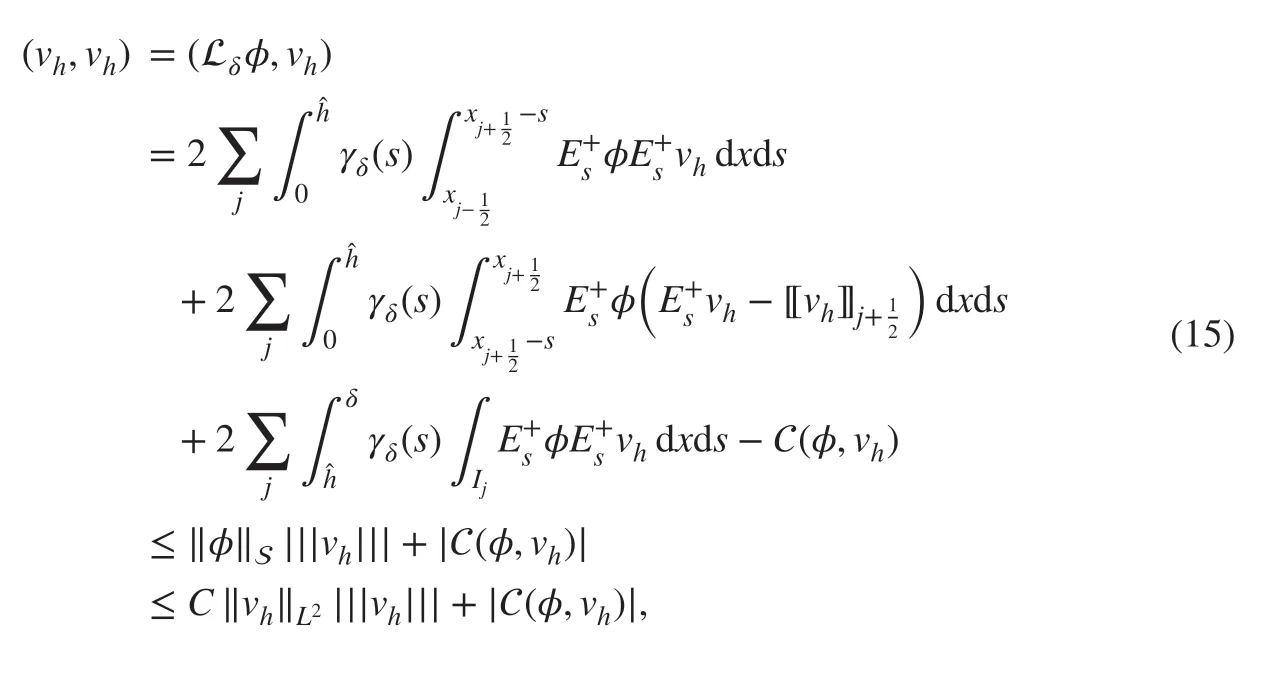
where C(φ,vh) is given as

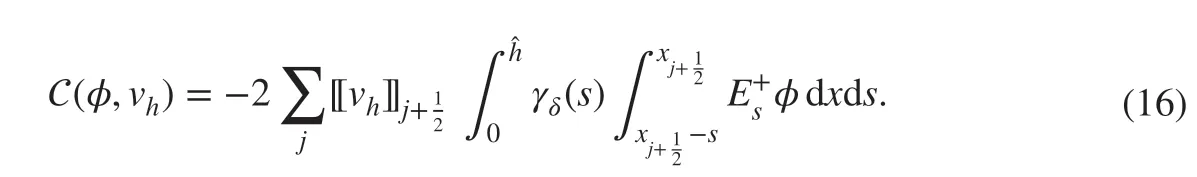
We then apply the following inequality (to be shown in Lemma 4.2 later in the section):

and plug ( 17) into ( 15) to get the discrete Poincaré's inequality ( 14).

Before proving the inequality ( 17) used in the proof above, we f irst explain the idea behind the proof. Let us think about the local limit, namely for δ small, the term

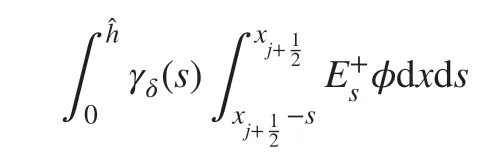
is essentially bounded by ‖φ‖C0,1, since we have

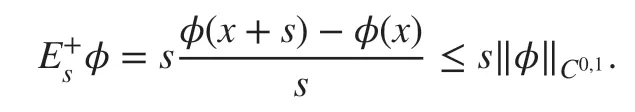
By the Sobolev embedding theorem (or trace inequality), we have

The elliptic regularity can then be applied to conclude that ‖φ‖H3∕2≤C‖vh‖L2thus completing the proof, as argued in [ 2]. For the situation considered here, a diffi culty is to obtain( 17) with a uniform constant C. Indeed, for each f inite δ＞0 , there is not enough elliptic regularity to make the argument in general. We thus have to avoid relying on the type of inequality as ( 18). Hence, we f ind another way to show the results in 1d that is analogous to the PDE counterpart in [ 2]. We use the fundamental theorem of calculus; we could rewrite φ′(x) as

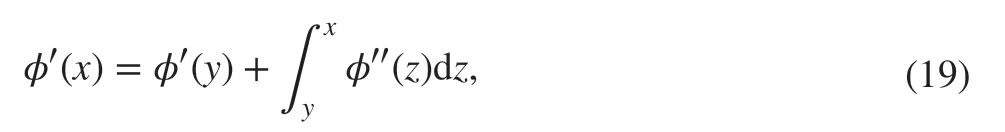
which is true for all y. Also, notice that in the local limit φ satisf ies the problem-φ′′(z)=vh(z) . Now, we integrate y on some interval I and obtain

Here, we can bound |φ′(x)| by the H1norm of φ and the L2norm of ‖vh‖L2and f inally, we can use an energy inequality to bound |φ|H1by ‖vh‖L2. In the following lemma, equality( 21) can be understood as an analog of ( 19).

Lemma 4.2Assume that φ∈L solves the problem Lδφ=vh, then we have, for some constant C＞0 , independent of δ and h,

where C(φ,vh) is def ined in ( 16).

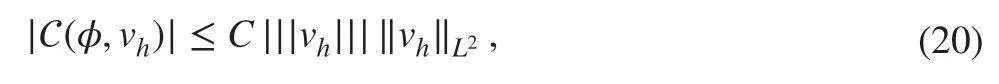
ProofFirstly, with=φ(y)-φ(y-s) , we can write

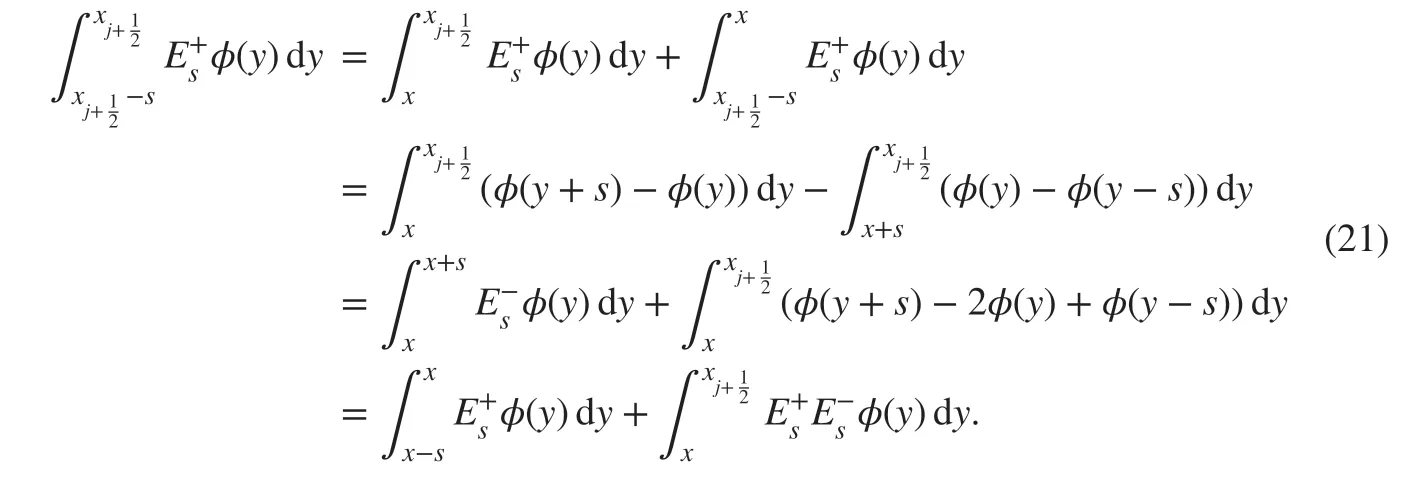
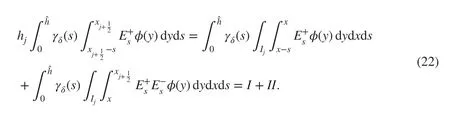
By changing the order of the integration in I, we have

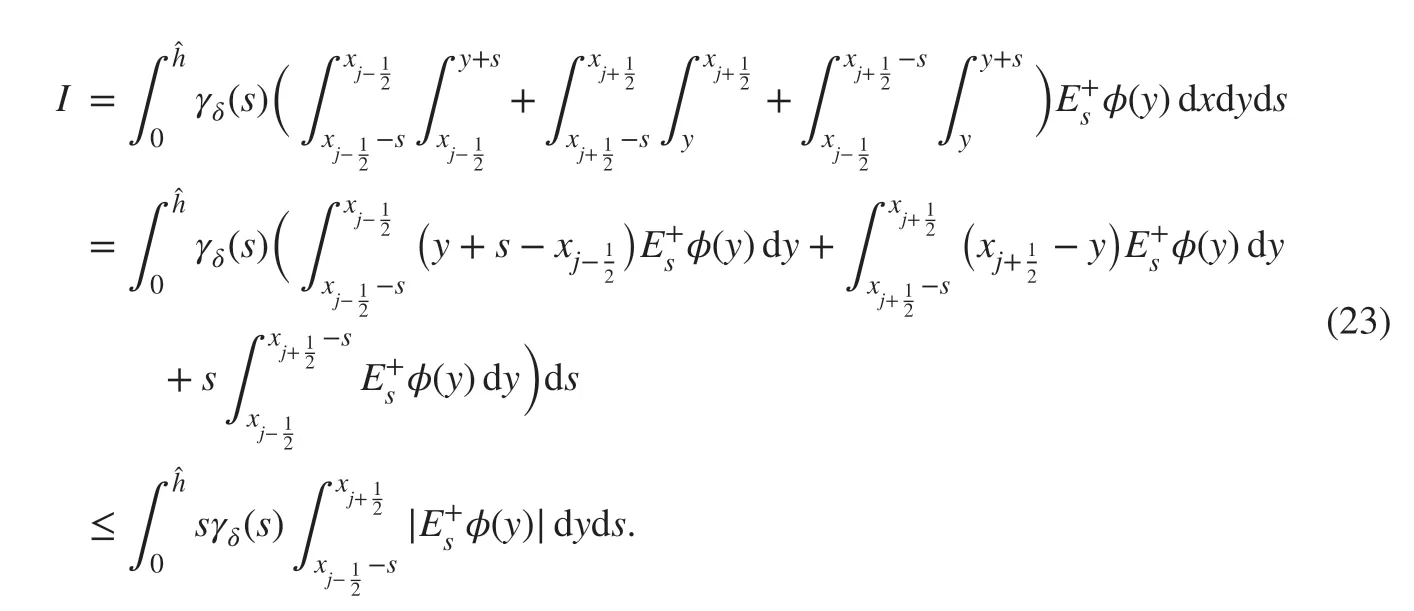
Similarly, by changing the order of the integration in II, we have

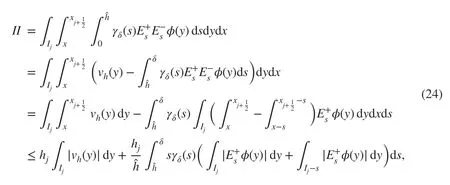
Therefore, with ( 25) we have

By the Cauchy-Schwarz inequality, we then have

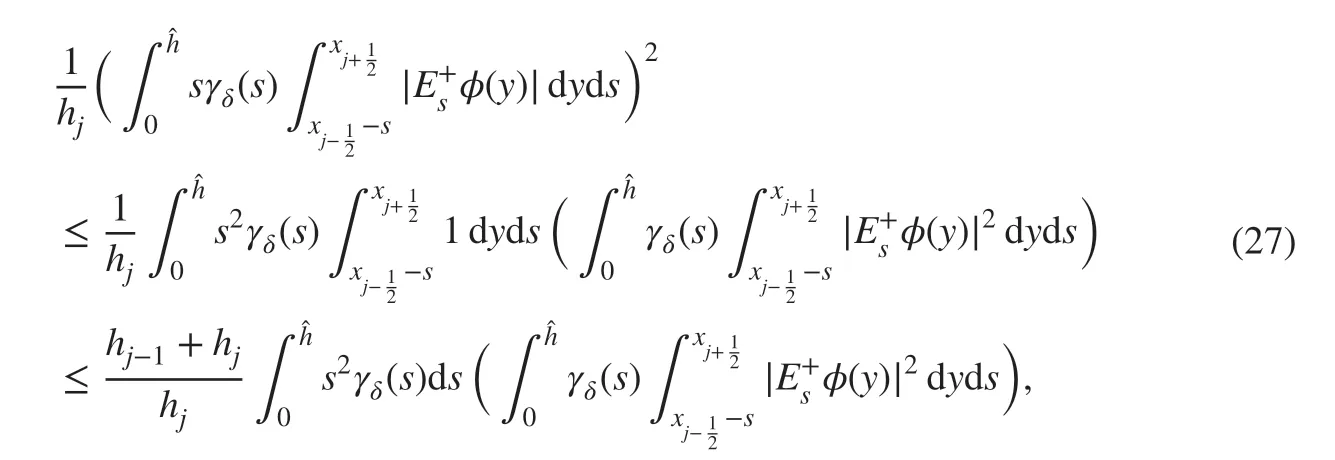
and

and P

lugging ( 27)-( 29) into ( 26), we then obtain

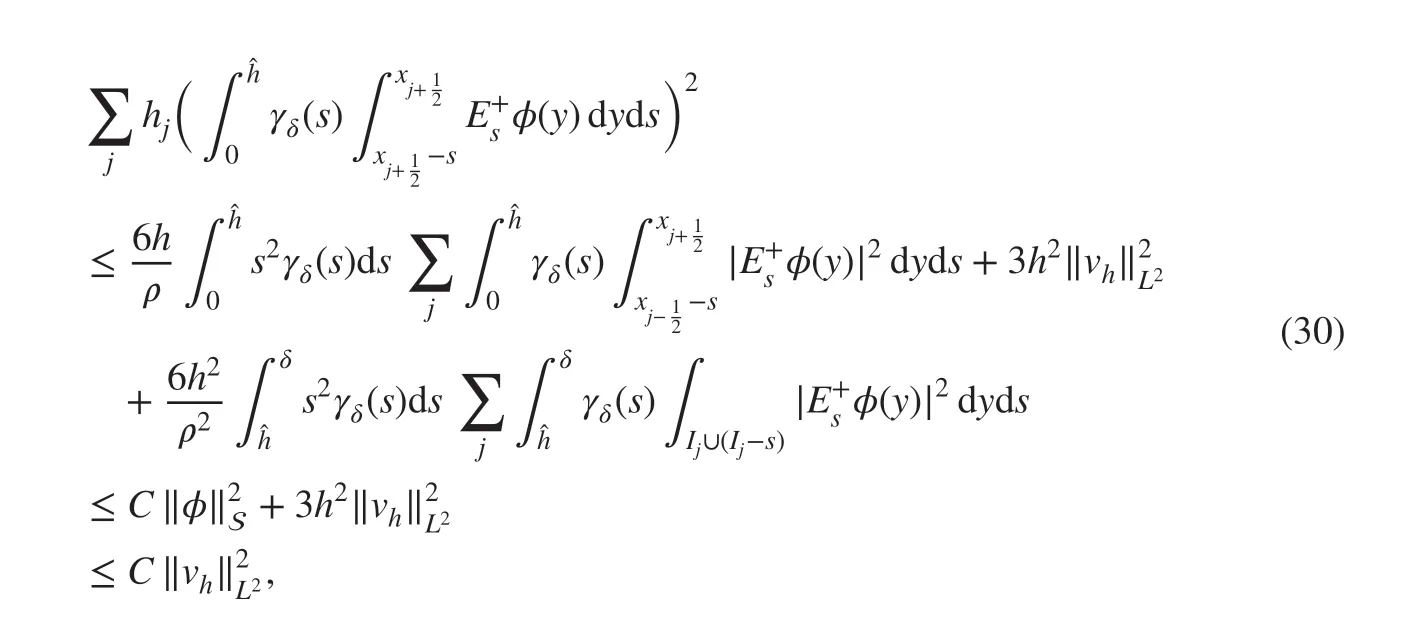
where C depends only on ν , a positive constant given in the assumption on the regularity of the mesh partition. Therefore, by the Cauchy-Schwarz inequality again, we f inally get

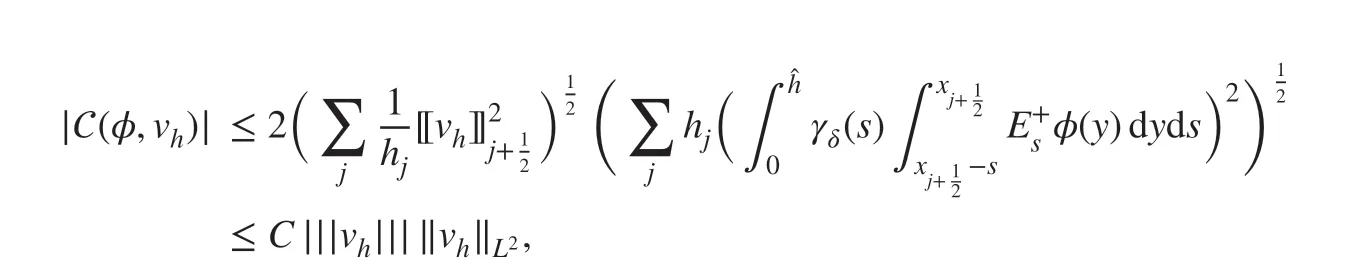
which completes the proof.

Proposition 4.1For the general kernels γδsatisfying ( 3), it holds that for some constant C＞0 uniformly in δ and h,

ProofConsider a cutoff of γδas follows:

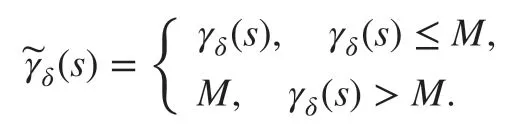
Take M＞0 suffi ciently large such that

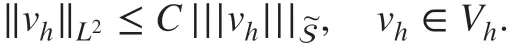
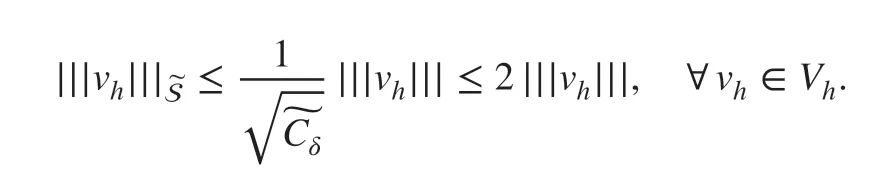
Then, we obtain the desired inequality ( 31).

4.2 Boundedness, Stability, and a Priori Error Estimates for the DG Scheme ( 11)

From the def inition of Bh(·,·) , it is straightforward to obtain the boundedness and stability results represented in the following:

Note that ( 32) also holds for v,w∈L . Now, let us take the continuous interpolant uI∈Vhof the exact solution u such that u-uI∈L and the jumps of u-uIare zero at the element interfaces. Note that this can be easily achieved when the exact solution u is smooth enough and k≥1 where k is the degree of the polynomials in Vh. Then, we have the following approximation property:

where C＞0 is independent of h and δ.

Corollary 4.1Let δ be f ixed. Then, it holds that when the kernel γδ(s)∈(ℝ) ( i.e., integrable kernel),

and sγδ(s)∈(ℝ) ( i.e., f inite f irst moment),

To derive the error estimates, we f irst need the following lemma.

Lemma 4.3For the solution u is smooth enough, we have that B(u,vh) in ( 8) is well def ined. Moreover,

ProofRecall the construction in ( 9) given by B(u,v)=B1(u,v)+B2(u,v)+B3(u,v) . We consider the terms separately with v =vh. By the Cauchy-Schwarz inequality, we have

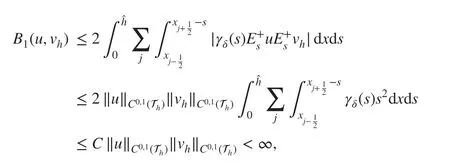
where

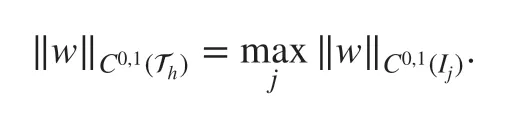
Meanwhile, we have

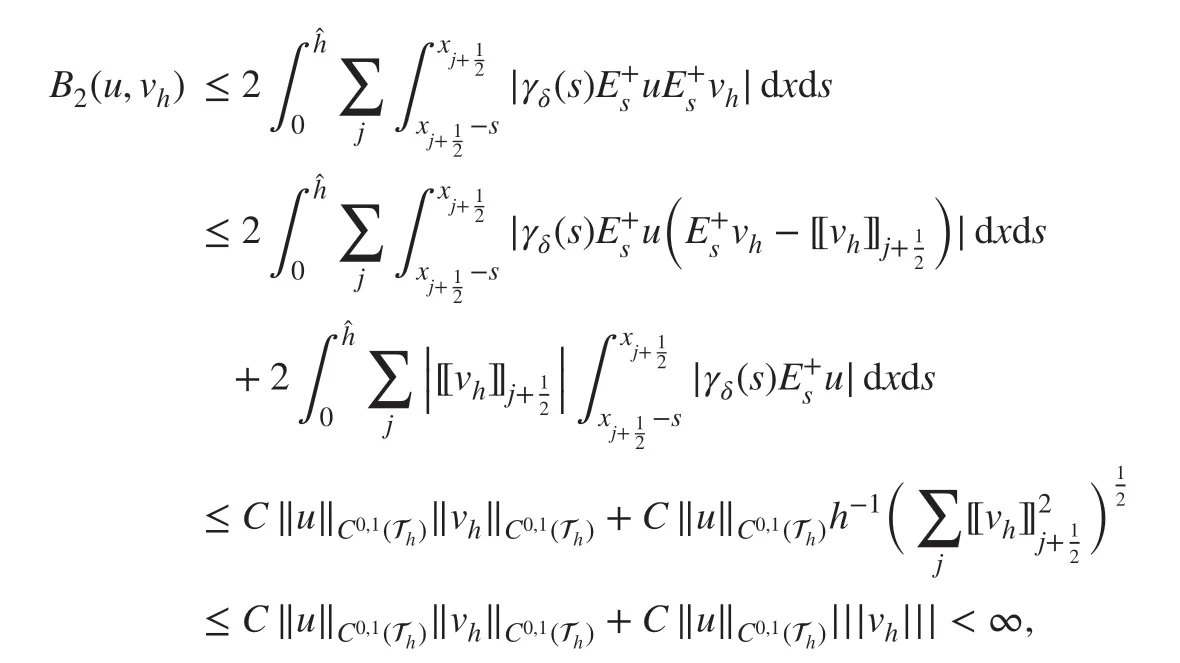
with μj=ηh-1and η is suffi ciently large. For B3(u,vh) , if=δ, then B3(u,vh)=0 . When^h=then we have

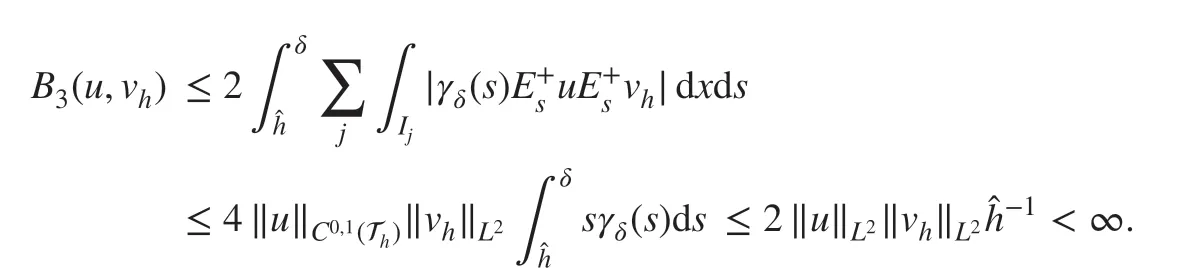
Thus, B(u,vh) is well def ined.

In the following, we show that B(u,vh)=(Lδu,vh)=(f,vh) for any vh∈Vhwhen u is smooth enough. Indeed,

As we can see, even when the solution u is smooth enough, the DG approximation of B( u, v) is generically not consistent, i.e.,

where C(u,vh) is the inconsistent term given in ( 16). Since the DG scheme ( 11) is not consistent, to derive the error estimates, we then need to estimate the inconsistent errors. The so-called superpenalty technique is adopted to control the inconsistent term C(u,vh) . We present the error estimates of the DG scheme ( 11) in the following theorem.

Theorem 4.1For the DG scheme ( 11) with the f inite element space Vhdef ined in ( 7) with k≥1 and μj=, there exists a unique approximate solution uh∈Vh. Assume that the exact solution u of the problem ( 1) is smooth enough, then we have the following a priori error estimate:

ProofWe f irstly consider the estimate of C (u,vh) . With the Cauchy-Schwarz inequality and Sobolev's inequality, we obtain

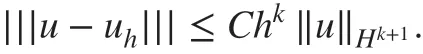
Therefore, we have

In ( 38), we have used the relation in Lemma 4.3 that

Then, by ( 38) and the triangle inequality, we obtain

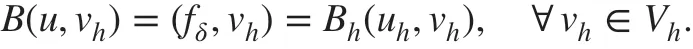
As μj=, then it implies β(^h,δ)≤Chk‖u‖H2. This completes the proof.

From ( 37), it is easy to f ind that diff erent μjwill lead to diff erent estimates for β(^h,δ) .We state it in the following corollary.

Corollary 4.2Under the conditions in Theorem 4.1, if the kernel γδ(s)∈(ℝ) and δ be f ixed , we have

and consequently plugging it into ( 39) gives

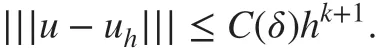
If sγδ(s)∈(ℝ) , we have

which then gives

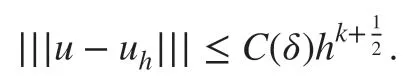
The asymptotic compatibility is a nice property to have, since the solutions of some numerical methods may converge to the wrong limits if one let hj,δ→0 [ 33]. For the scheme that is asymptotically compatible, the numerical solution will converge to the exact solution of the local problem when hj,δ→0 simultaneously, i.e.,

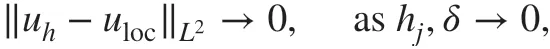
where ulocis the exact solution to the local counterpart of the problem ( 1). For more details,one may refer to, e.g., [ 34]. To obtain the asymptotic compatibility of the DG scheme ( 11),we need a known result (e.g., see [ 13]) that

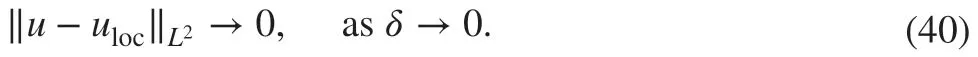
Meanwhile, we further assume that there exists C0＞0 is a constant such that

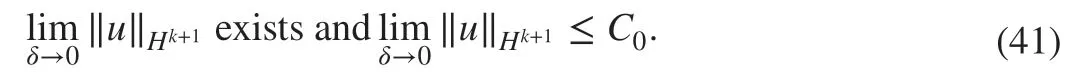
Corollary 4.3Assume ( 41) holds. Under the conditions in Theorem 4.1, the scheme ( 11) is asymptotically compatible.

ProofFrom ( 38), we have

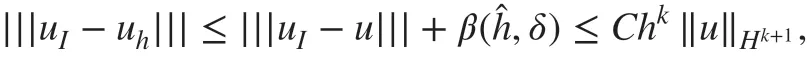
where the constant C is independent of δ and h. By the discrete Poincaré's inequality ( 31),we have ‖uI-uh‖L2≤C|||uI-uh|||≤Chk‖u‖Hk+1. Together with the approximation property ( 34), we have

Together with ( 40) and ( 41), we then obtain the desired result.

Remark 4.1In the local case, to obtain the error estimates in the L2norm, we need to utilize the dual problem in the derivation. However, since the nonlocal problem does not have the elliptic regularity theory as in the local case, any extra regularity of the exact solution in ( 1) is not expected; thus the duality argument may not work for general nonlocal diff usion problems. On the other hand, when δ is f ixed and γδ(s) is integrable, the energy norm|||·||| is equivalent to the L2norm, which leads to the error estimates in the L2norm.

4.3 L2-Stability and a Priori Error Estimates for the Semi-discrete DG Scheme ( 12)

Without loss of generality, let us set fδ=0 in ( 12). By taking vh=uhin ( 12) and using ( 31),we then obtain

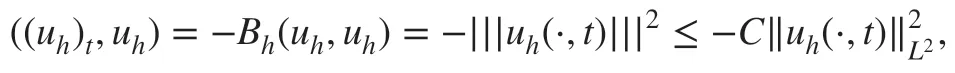
which implies

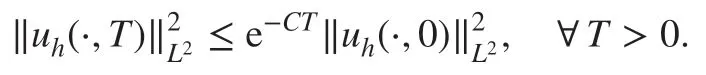
Therefore, the numerical solution uh→0 when the f inal time T →∞.

Next, we study a priori error estimates under the assumption that u is smooth enough. For simplicity, we use the notations as follows:

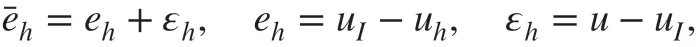
where uI∈Vhis an approximation to the exact solution u. With ( 5) and ( 12), we get the following error equation:

where C (u,vh) is the inconsistent term given in ( 16).

By taking vh=ehin ( 42), we have

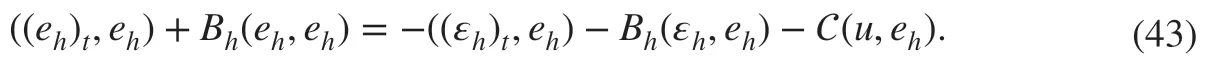
Let uI∈Vhbe a suitable interpolant of the exact solution u so that the approximation property ( 34) holds. By the Cauchy-Schwarz inequality and approximation property, we then have

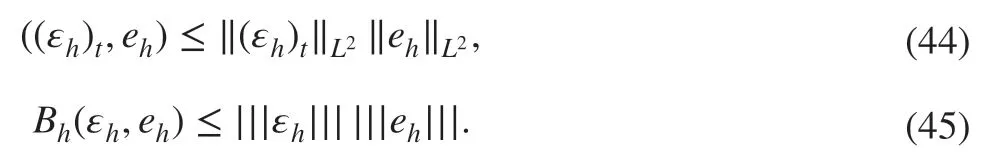
By plugging ( 36), ( 44), and ( 45) into ( 43) and using the Cauchy-Schwarz inequality and( 31), we can obtain

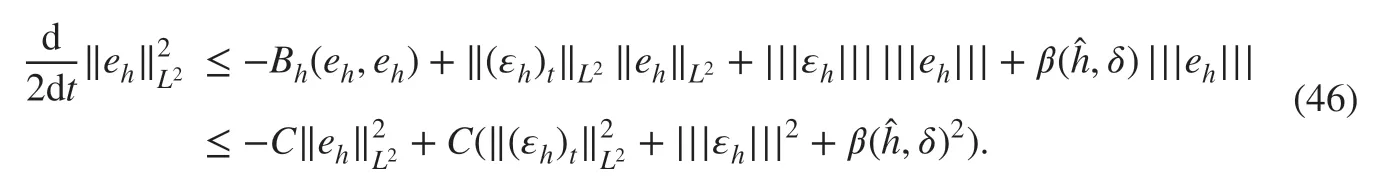
Thus, we obtain by applying Gronwall's inequality with ( 46)

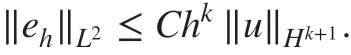
By the triangle inequality, f inally we have

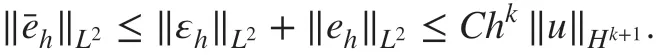
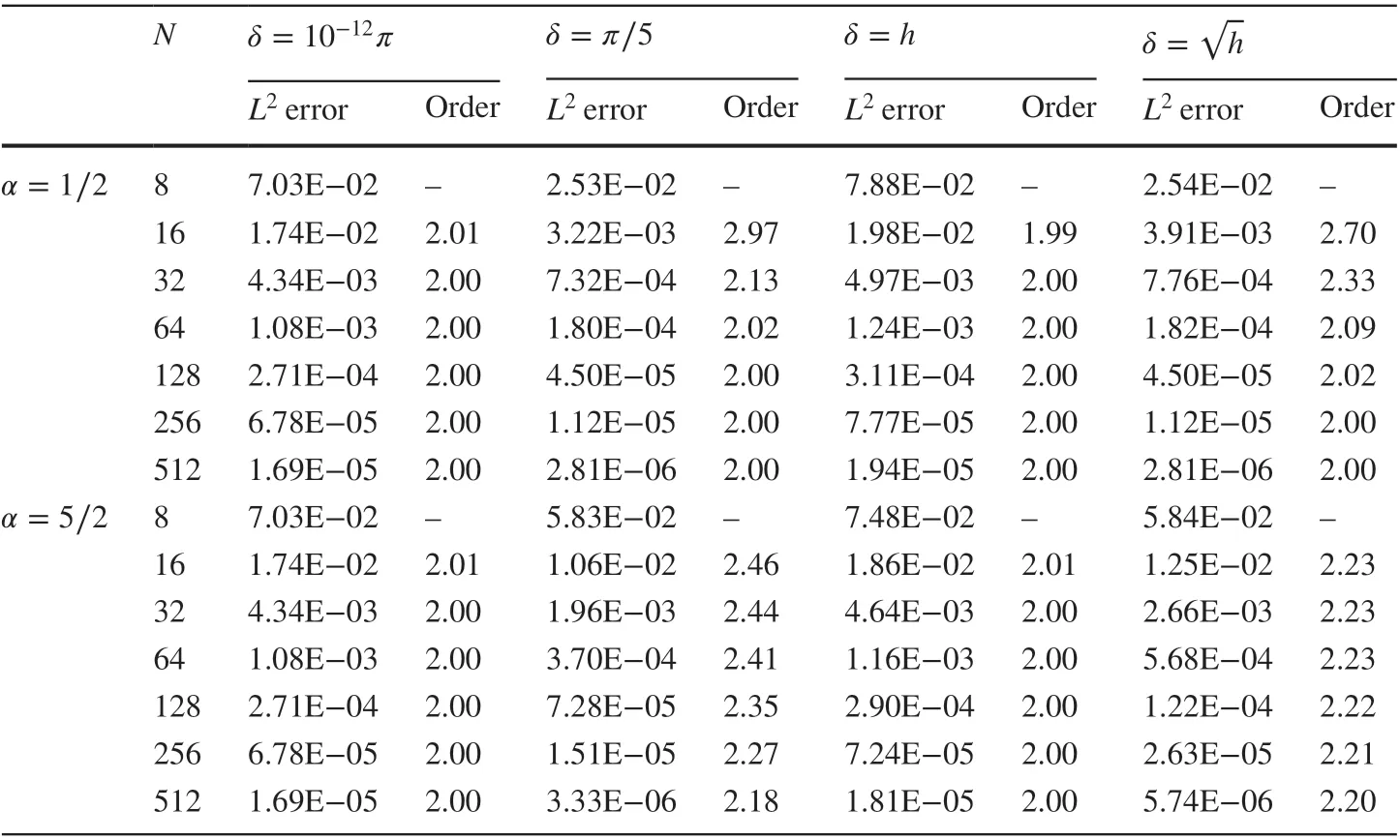
Table 1 L2 errors and convergence orders produced by the DG scheme ( 11) when k=1 in Example 1

Table 2 L2 errors and convergence orders produced by the DG scheme ( 11) when k=2 in Example 1

Table 3 Errors and convergence orders of |||uI-uh||| produced by the DG scheme ( 11) when k=1 in Example 1

Theorem 4.2Let uh(·,t)∈Vhbe the approximate solution generated from the semi-discrete DG scheme ( 12), with the f inite element space Vhdef ined in ( 7) and k≥1 . Then, we have the following stability result:

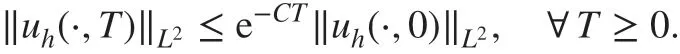
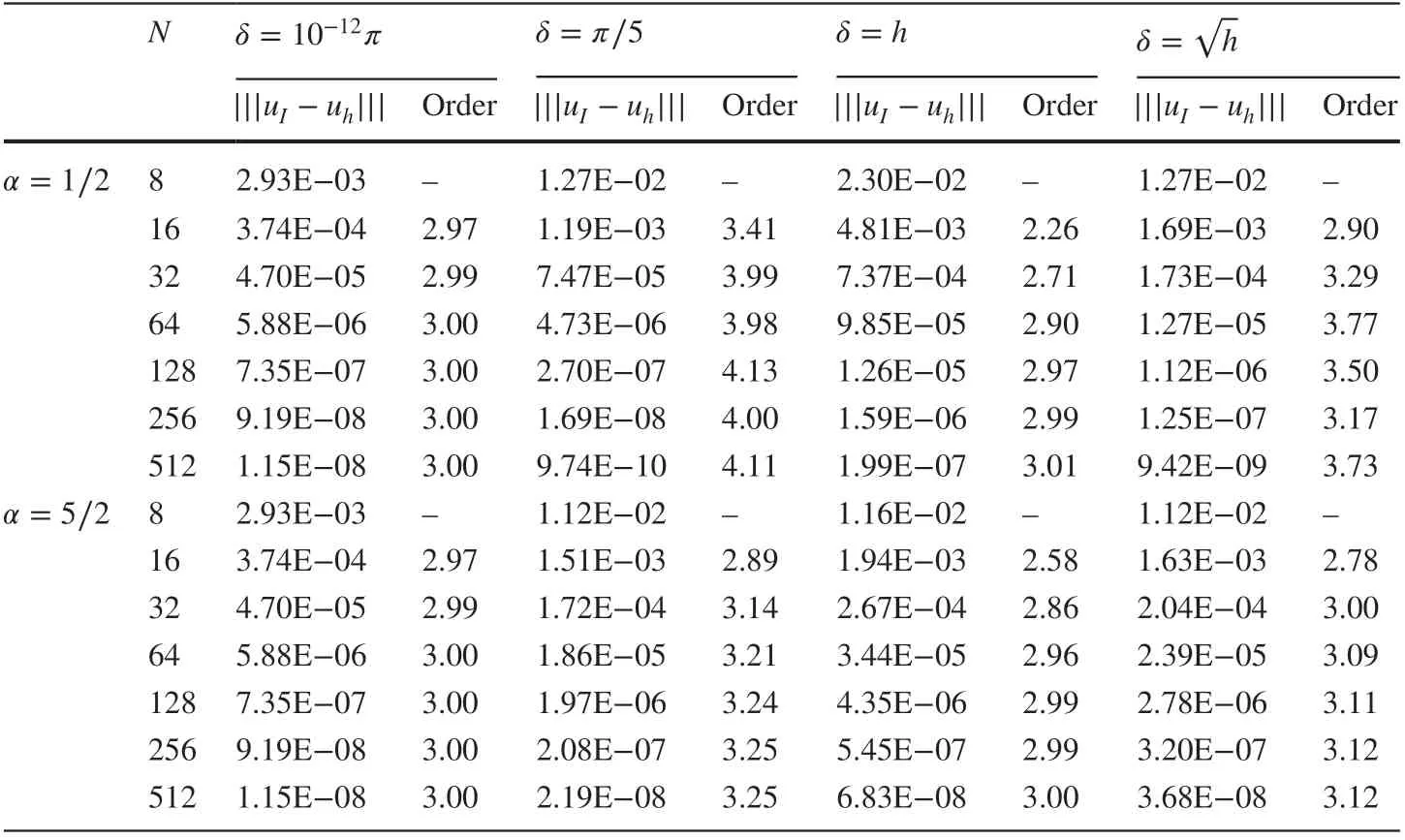
Table 4 Errors and convergence orders of |||uI-uh||| produced by the DG scheme ( 11) when k=2 in Example 1

Moreover, assume that the exact solution u(·,t) of the problem ( 2) is smooth enough, then we have the following error estimate:

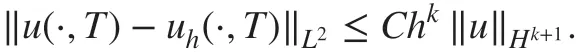
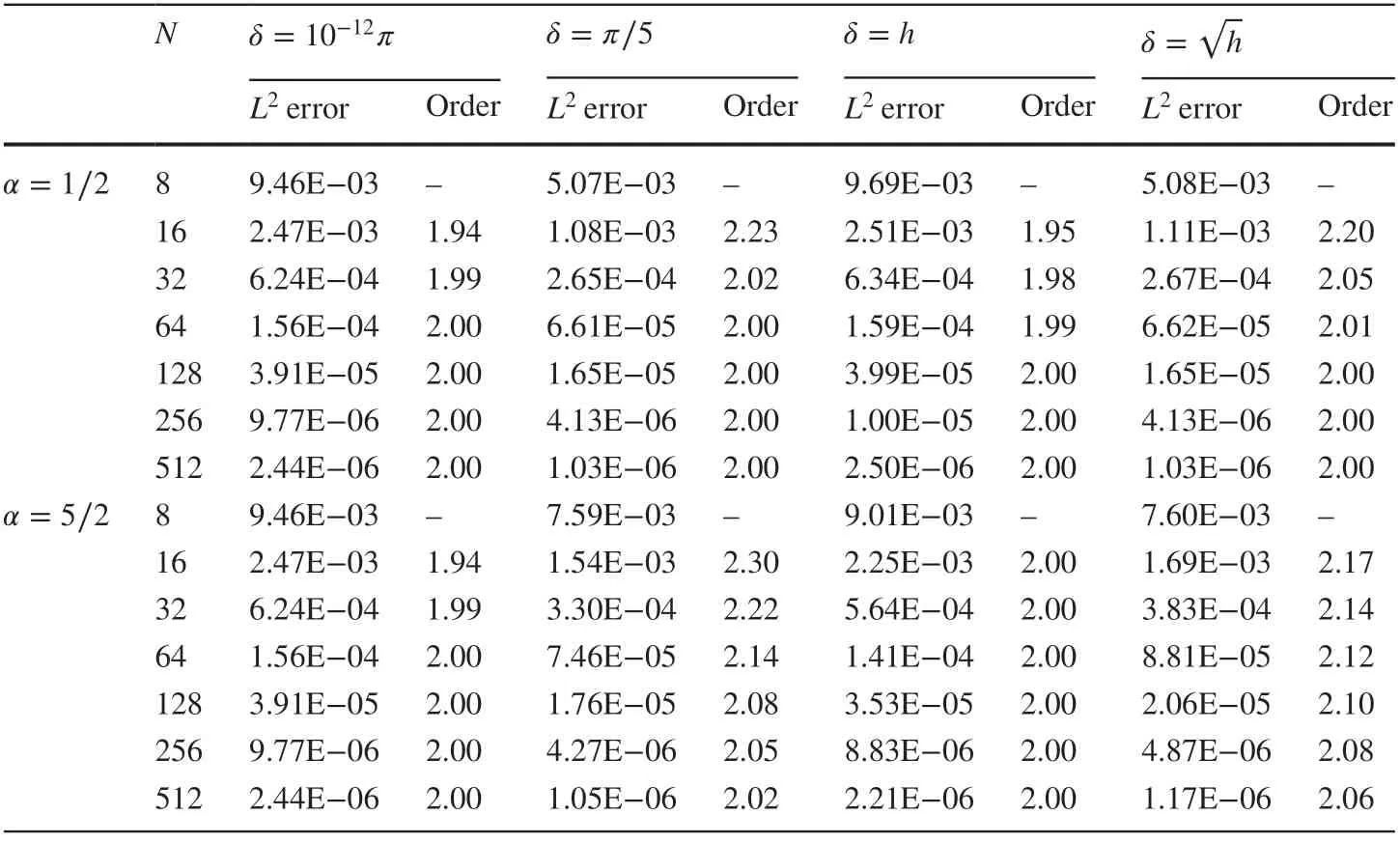
Table 5 L2 errors at the f inal time T=1 and convergence orders produced by the semi-discrete DG scheme( 12) when k=1 in Example 2

Table 6 L2 errors at the f inal time T=1 and convergence orders produced by the semi-discrete DG scheme( 12) when k=2 in Example 2

Corollary 4.4Under the conditions in Theorem 4.2 and δ is f ixed, then it holds that when the kernel γδ(s)∈(ℝ),

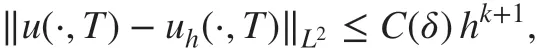
and when sγδ(s)∈(ℝ),

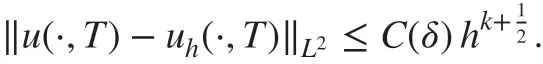
5 Numerical Experiments

In this section, we present some numerical experiments to verify the theoretical results.The kernel function for all examples is chosen to be

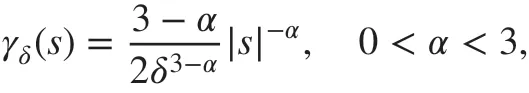
The latter two cases are used to test the asymptotic compatibility of the proposed DG schemes. We also test two diff erent values for α : α =1∕2 and α =5∕2 . It is easy to see γδ(s)∈(ℝ) when α =1∕2.

Table 7 L2 errors and convergence orders produced by the DG scheme ( 11) when k=1 , μj≡μ=3h-1 in Example 3

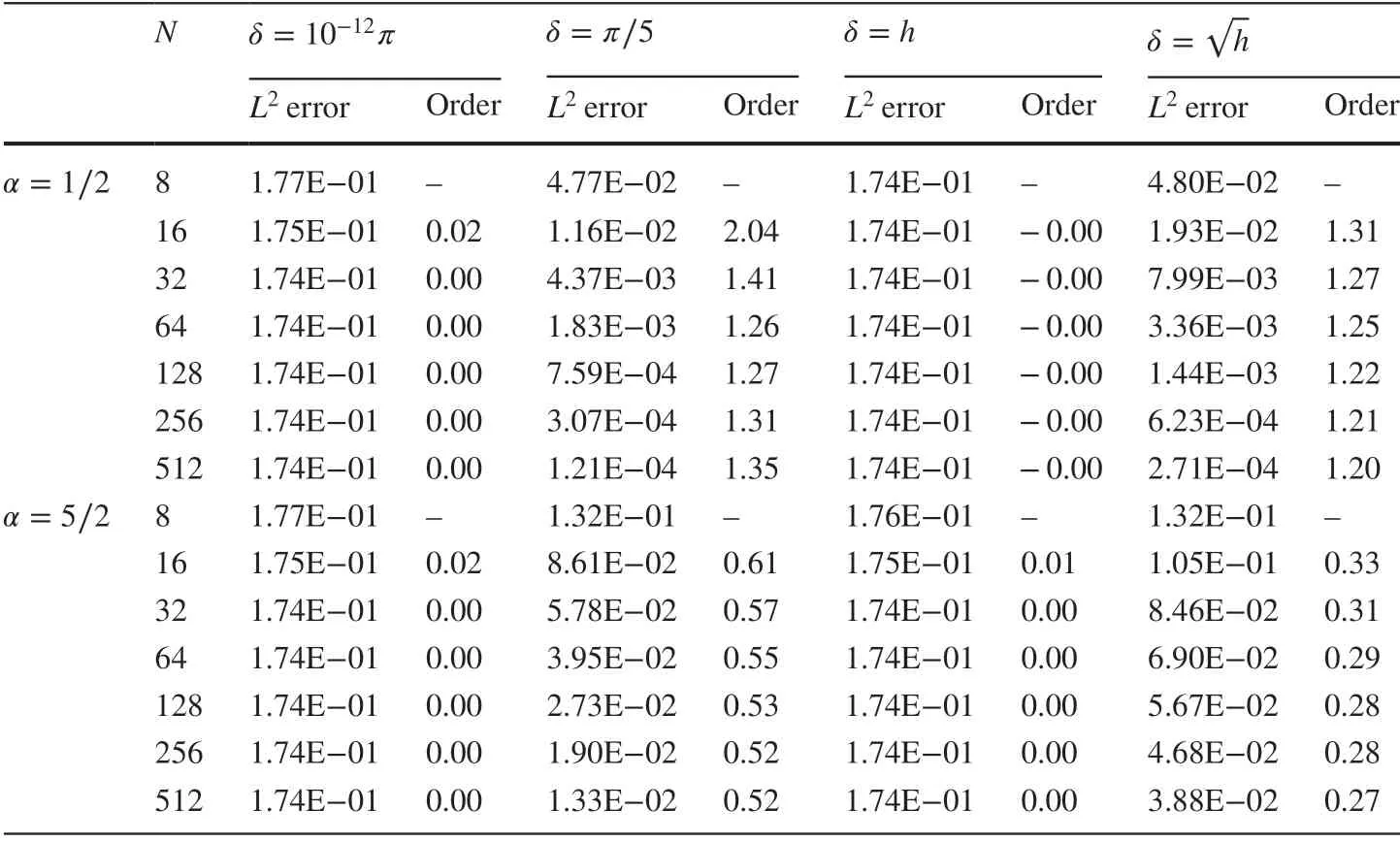
Table 8 L2 errors and convergence orders produced by the DG scheme ( 11) when k=2 , μj≡μ=3h-1 in Example 1

Example 1For the steady-state problem ( 1), we take the source term as

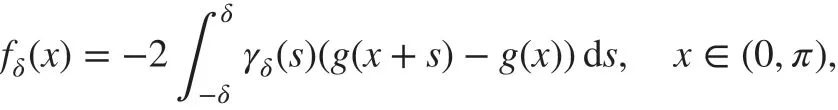
where g( x) is def ined by

Thus, the exact solution is u(x)=g(x).

Numerical results for Example 1 computed by the DG scheme ( 11) for the steady-state problem are reported in Tables 1, 2, 3, and 4. It is observed that the DG scheme achieves the optimal convergence of order k+1 for the Pk-element ( k=1,2 ) in the L2norm for all cases, even though the kernel function γδis not integrable when α=5∕2 . Besides, we also compute |||uI-uh||| where uIis the continuous interpolation of the exact solution u and report the errors and convergence orders in Tables 3 and 4. In particular, the results with δ=h and δ =verify that the DG scheme is asymptotically compatible.

Example 2For the time-dependent problem ( 2), we set the initial condition to be

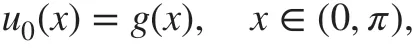
and the source term fδto be

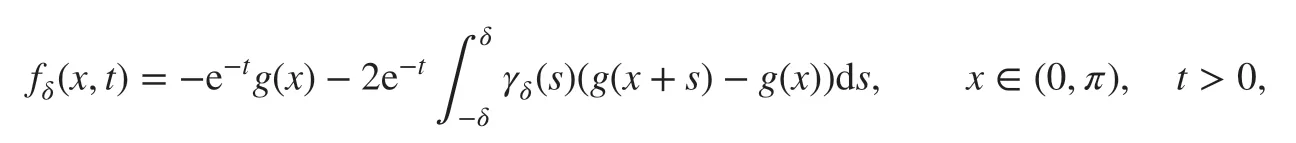
where g( x) is def ined in Example 1. Thus, the exact solution is u(x,t)=e-tg(x) . We adopt the third-order singly diagonal implicit Runge-Kutta (SDIRK) method with two stages as the time-stepping method [ 22, 23]. We take the time step size τ=h∕π and the f inal time is T=1.

Numerical results for Example 2 computed by the semi-discrete DG scheme ( 12) for the time-dependent problem are reported in Tables 5 and 6. We again observe the similar convergence behavior as that in Example 1.

Example 3Our last example is to reconsider Example 1 with the penalty parameter μj=O(h-1) , instead of the μj=O(h-2k-1).

Tables 7 and 8 report the numerical results produced by the DG scheme ( 11) with the penalty parameter μj=O(h-1) . From the results, we can see that the L2errors heavily depend on the penalty terms and also depend on the choices of δ and α in γδ(s) given in the beginning of this section. It can be explained by the estimates of β(^h,δ) in ( 37) when diff erent γδ(s) and μjare chosen. Therefore, although we have the stability of the DG scheme ( 11) when μj＞0 , the accuracy could degenerate if μjis not large enough.

6 Concluding Remarks

In this paper, we propose and analyze a new discontinuous Galerkin (DG) method for onedimensional nonlocal diff usion problems. We f irstly identify the term in the nonlocal integral that requires particular treatment. We then introduce a jump into this term to overcome the singularity of the kernel function. Since the resulting formulation is not consistent, we add a penalty term in the proposed DG scheme to control the inconsistency error. Based on the dual problem, we prove the Poincaré's inequality at the discrete level for the proposed scheme, which plays an important role in further stability and error analysis. For the steady-state ND problem, we obtain the stability, boundedness, and a priori error estimates of the DG scheme. In particular, the error estimates imply the DG scheme is asymptotically compatible. For the time-dependent ND problem, we establish the L2-stability and a priori error estimates of the semi-discrete DG scheme. Numerical experiments show that the proposed DG schemes achieve the optimal order of convergence.

Considering the new contributions in the current work and studies in the past, we have developed two types of DG schemes for the ND problems: one is to use auxiliary variables[ 14] and the other is the one with penalty developed here. Since these two DG schemes both have their respective limitations, it is desirable to develop a unif ied framework for the DG schemes for the ND problem in the future work, as in [ 1] for local models. In addition,the present work is focused on one-dimensional ND problems, and its extension to multidimensional problems remains an interesting ongoing research work.

AcknowledgementsQ. Du's research is partially supported by US National Science Foundation Grant DMS-1719699, US AFOSR MURI Center for Material Failure Prediction Through Peridynamics, and US Army Research Offi ce MURI Grant W911NF-15-1-0562. L. Ju's research is partially supported by US National Science Foundation Grant DMS-1818438. J. Lu's research is partially supported by Postdoctoral Science Foundation of China Grant 2017M610749. X. Tian's research is partially supported by US National Science Foundation Grant DMS-1819233.