制动盘模态的数值分析与试验研究

2020-03-25陈国强李晓峰周龙

河南理工大学学报(自然科学版) 2020年3期

陈国强，李晓峰，周龙

(河南理工大学机械与动力工程学院，河南焦作 454000)

0 引言

制动器主要包括盘式制动器和鼓式制动器两类，盘式制动器具有良好的通风散热性与稳定性,并且制动迅速、维修方便，在汽车、矿山机械、航空等领域得到了广泛应用[1-3]。盘式制动器主要由制动盘、摩擦片、制动钳、油管等组成，在实际工作中，液压系统把压力施加在摩擦片上，使摩擦片与制动盘发生摩擦，从而产生制动力，使汽车减速，直至停下。当引入摩擦力时，整个制动系统会发生模态耦合现象[4-6]，而当制动盘固有频率与制动器其他零部件固有频率相同或接近时，会发生共振，不仅会产生噪声影响乘客的乘车舒适性，而且还会影响汽车制动的安全稳定性，因此，有必要对制动盘的模态进行分析研究。

模态分析常用的方法有数值模态分析与试验模态分析[7-8]。数值模态分析是在已知模型详细材料参数、边界条件等情况下，利用有限元分析软件进行理想情况下的模态分析。而在模型材料参数和边界条件未知或缺失的情况下，可以利用试验模态分析对系统的输入输出信号进行参数识别，对有限元模型进行参数修正，使有限元模型更加符合实际情况。

为提高制动系统的稳定性，减小制动噪声，学者们对制动系统进行了一系列的研究。张立军等[9]通过建立制动盘有限元模型，探索了制动盘弹性模量对自由模态和约束模态的影响，进而分析了制动盘弹性模量对制动尖叫的影响；吕辉等[10]提出一种基于响应面法和优化技术相结合的方法，通过优化系统的不稳定系数，对系统的噪声进行抑制；N.K.Kharate等[11]建立了盘式制动器各零部件的有限元模型，探讨了各零部件在不同材料参数下制动盘的尖叫特性，并通过试验模态进行了分析验证；T.J.Mrio等[12]建立了制动器的有限元模型，讨论了摩擦系数、制动压力以及制动温度对系统复模态的影响，并通过应力-应变装置对制动系统的接触刚度进行了试验分析；A.Karamoozian等[13]对一种新型格栅式结构的制动盘进行了有限元建模和自由模态试验分析，并用复模态分析方法探讨了新型格栅式结构制动盘与传统厢式制动盘产生噪声倾向性的大小。

以上研究主要集中在盘式制动器模态理论分析方面取得了研究成果。本文利用有限元法对制动盘的自由模态和约束模态进行仿真分析，并联合多种测试软件搭建便携式模态测试平台，利用试验的方法对制动盘自由模态进行分析。通过后期数据的处理、对比、分析，验证有限元模型的正确性，为制动盘的结构改进、新材料的选用以及提高系统的噪声稳定性提供理论依据。

1 有限元模型的建立

对制动盘进行有限元建模时，为节约计算时间，需要对模型进行一定的简化处理，去掉模型中不必要的倒角、圆孔等细节。把简化后的模型导入到ABAQUS 软件中，进行网格划分。划分的网格尺寸越小、数目越多，仿真结果就越可靠，但计算成本也随之增大。本文采用六面体网格划分，相比四面体网格，在网格尺寸相同的情况下，网格数目更少，这意味着计算时间的减少，同时，精度却更高。网格类型采用C3D8I单元，网格尺寸4 mm，通常认为网格尺寸控制在3～5 mm时，结果是可靠的。网格的制动盘模型划分后，网格数目总共有6 959个，网格节点有10 395个，图1为制动盘的实物、几何模型与有限元模型。

图1 制动盘模型

划分网格之前，需要对制动盘有限元模型进行材料属性的定义。制动盘材料采用HT250，材料的具体参数如表1所示。ABAQUS软件没有固定的单位制，在进行材料赋予的时候，各个量的单位制要统一，只有单位制统一仿真结果才有意义，否则容易造成模型仿真结果不收敛。本文采用SI(m)单位制。

表1 材料参数

2 有限元模态分析

2.1 自由模态分析

自由模态分析在工程实践中应用广泛，通过模态分析，不仅可以改进机构的不合理设计，为结构的优化提供理论基础，而且还可以指导试验测试[14-15]。例如在自由模态测试中指导加速度传感器位置的放置、激励点的选择等，提高试验测试系统的便捷性与精确性。

制动盘有限元前处理完成之后，在ABAQUS求解器中设置Block Lanczos模态求解算法，提取前12阶模态，创建Job，提交之后就可以进行模态分析计算。由于本文求解的是制动盘的自由模态，前6阶为刚体模态，模态频率几乎为0，因此把第7阶当作第1阶模态进行讨论分析。表2为制动盘第7阶起的后6阶模态频率及其所表现出的振型描述。

表2 自由模态频率与振型

制动盘为典型的循环对称结构，存在大量的重根模态，因此，对制动盘的振型采用节圆-节径(m，n)的方法进行描述，其中m表示节圆，n表示节径。制动盘的振型为(m，0)，表示制动盘只有m节圆的轴向模态；(0，n)表示制动盘只有n节径的周向模态；(m，n)表示制动盘既有m节圆的轴向模态又有n节径的周向模态。图2为节圆-节径的典型振型图。

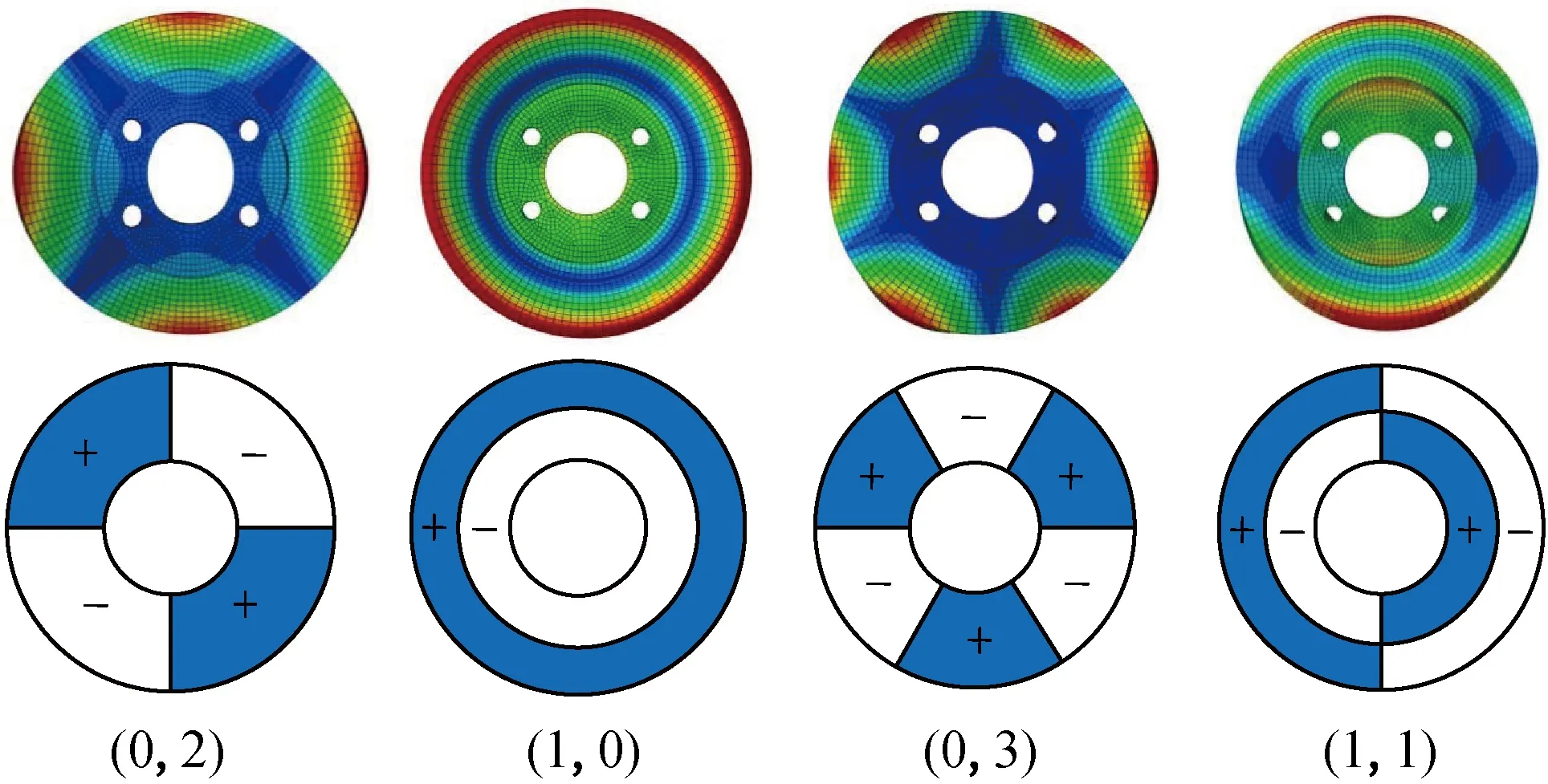
图2 节圆-节径示意图

图3为有限元分析计算出的制动盘第7阶起的后6阶模态振型图。制动盘的第1，2阶模态振型用节圆-节径可以表述为(0，2)，都拥有2个节径的周向模态，每个节径之间相差π/4，制动盘的变形沿z轴方向上下振动；制动盘第3阶模态振型可以表述为(1，0)，拥有1个节圆的轴向模态，制动盘的变形同样也是沿z轴方向上下振动；第4，5阶模态的振型是(0，3)，拥有3个节径的周向模态，每个节径之间相差π/6，制动盘的变形同样沿z轴方向上下振动；第6阶模态的振型为(1，1)，表示既拥有1节圆的轴向模态又拥有1节径的周向模态，制动盘的变形为盘帽沿z轴上下摆动。从6阶振型图可以看出，制动盘的变形主要发生在盘面周围，表现为端面跳动，在制动过程中容易和摩擦片发生模态耦合而产生共振。

图3 制动盘前6阶(第7阶为第1阶)固有振型图

2.2 约束模态分析

在实际工作过程中，制动盘是通过螺栓孔与轮毂相连而随之转动的，为了模拟实际情况下的工作状态，需要对刹车盘进行约束处理，因此，需要限制4个螺栓孔在x，y，z方向上的位移，具体约束处理如图4所示。

图4 约束的施加

同样地，在ABAQUS求解器中设置Block Lanczos模态求解算法，提取前12阶模态，创建Job并提交之后，进行制动盘约束模态的分析计算，表3为制动盘前12阶约束模态计算结果。从表3可以看出，制动盘在约束状态下，前6阶模态由刚体模态转换为弹性模态，从第7阶开始，制动盘的约束模态频率普遍比自由模态的高，这是因为约束之后，制动盘的刚度增加。约束模态通常通过限制制动盘某个方向的自由度而表现出来，当某个方向自由度未被限制时，某阶约束模态会和自由模态接近。例如约束状态下的第6阶模态频率(2 293.8 Hz)和自由状态下的第5阶模态频率(2 268.9 Hz)误差不超过1%，而且振型也完全相同，都是拥有3个节径的周向模态。

表3 制动盘前12阶有限元约束模态

3 自由模态测试

3.1 系统组成

为测量制动盘固有频率，搭建了基于LabVIEW软件的自由模态测试平台，该测试平台包括硬件和软件两部分，图5为系统组成框图。硬件部分包括稳压电源、传感器恒流适配器、CT1050LC加速度传感器、力锤、制动盘、NI USB-6002采集卡等。软件部分包括程序编写软件LabVIEW、数据分析软件MATLAB以及数据显示软件Origin等。

图 5 系统组成框图

CT1050LC加速度传感器采用具有压电效应的材料，如石英晶体、压电陶瓷晶体作为敏感元器件，抗干扰能力强、灵敏度高(490 mV/g)、频率响应范围宽(0.5～3 000 Hz)、动态特性好，广泛应用于振动、冲击等动态测试场所。数据采集卡采用美国国家仪器(NI)有限公司生产的多功能I/O设备NI USB-6002，该采集卡是一款低成本便携式多功能信号采集器，采用总线供电，方便使用，具有8路16位50 kHz的模拟量输入口、2路模拟量输出口、13路的数字输入/输出口和一个32位的计数器，加速度传感器可以方便地连接到NI USB6002采集卡。NIDAQmx可方便地实现配置和测量，实现硬件和软件的无缝衔接。图6为搭建的信号采集系统。

图6 信号采集系统

3.2 系统实现

锤击法[16]是自由模态试验中最常采用的方法，适合用于体积小、结构简单的构件上，通过对构件进行敲击，同时，利用传感器获取系统的输入输出信号。根据有限元仿真结果可以看出，制动盘是一个循环对称结构，会存在很多节圆节径，为了保证不漏阶，需要布置多个测量点，采用单点锤击多点拾振的方法进行测量。对制动盘进行4等分，盘帽部测点从1～36沿周向均匀分布，同样盘面测点从37～60沿周向均匀分布，总共布置60个测量点，每个点测量3次，具体的测量点布置如图7所示。

图 7 测点布置图

试验中编写的信号采集程序如图8所示，采用图形化的程序语言进行编写。程序主要包括4部分，分别为通道设置、时钟设置、路径设置以及数据保存设置。在信号采集程序的前面板中设置采样通道、采样电压、采样频率、采样数等后，就可以进行信号采集，其中，为了保证信号不失真，根据奈奎斯特采样定理，采样频率设为9 kHz。在数据分析软件中对采集到的数据预处理，利用编写的快速傅里叶变换程序对数据进行频谱分析、参数识别等，以方便后续数据结果的对比分析。

图8 信号采集程序

4 测试结果与分析

传感器输出的电信号中通常混杂着干扰信号，需要去除噪声，提高信号抗干扰性和信噪比，而滤波是常用的抑制或消除噪声的主要手段之一。利用数值分析软件设计中的带通-巴特沃斯型滤波器，对采集到的信号进行滤波，该滤波器可以允许特定频段通过，而对其他频段进行抑制，且通带内具有最大平坦的频率特性，设计简单，容易实现。信号滤波之后，利用快速傅里叶变换对信号进行频谱分析。图9为某次测试经过带通滤波后1阶和3阶的频谱。试验时每个测量点敲击3次，可得到3个信号频谱图，从频谱图获取模态频率，对每阶模态频率的测试结果求均值，得到最终模态频率。制动盘前6阶固有频率见表4。

图9 信号频谱图

表4 仿真频率与实测频率

本次试验误差主要由以下几方面构成:一是测量仪器本身和人工读取数据时存在的误差，以及为了节约计算成本对模型进行适当的简化，去掉不必要的倒角和圆孔等而引起的误差；二是制动盘有锈蚀，材料属性、模型质量等可能发生轻微改变。误差是测试系统不可避免的，本次研究选用精度较高的传感器与数据采集卡，对每一阶的模态频率进行多点测量求平均值，以此提高测试精度。由于仿真是在理想情况下测出的，试验结果不可能和仿真结果完全相同，从表4可知，仿真数据和实测数据的误差均没有超过10%，而且最小误差为2.1%，在可接受范围内。