泰勒公式在不等式中的应用

游 扬

(福州外语外贸学院 公共教学部，福建 福州 350200)

随着互联网时代的到来，大学数学的教学改革应从“互联网+教学”角度出发，对高等数学的教学过程进行研究[1]；同时加强高等数学的素质教育，以培养创新型人才[2].泰勒(Tayloy)公式是高等数学课程中的重要内容，也是研究函数常用的工具之一.在高等数学中，不等式的证明方法有很多，如果不等式中包含一阶及二阶等高等级导数时，就需要用泰勒公式来证明.为了帮助学生学习高阶导数，石秀文[3]使用泰勒公式对不等式进行证明，并总结出一些规律和技巧.本文在介绍泰勒公式的基础上，对泰勒公式在不等式中的应用进行分析.

1 泰勒(Tayloy)公式

在高等数学中，泰勒公式是一个用函数在某点的信息来描述其附近取值的公式.其中，带有佩亚诺型余项的泰勒公式和带有拉格朗日型余项的泰勒公式应用较广[4].

1.1 带有佩亚诺型余项的泰勒公式

若函数f(x)在点x0处存在直至n阶导数，则x0的邻域内有：

(1)

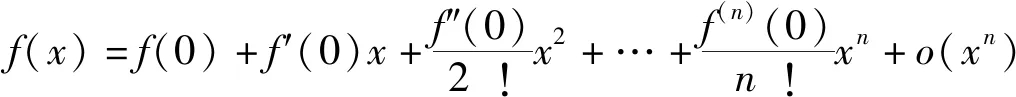
(2)

1.2 带有拉格朗日型余项的泰勒公式

若函数f(x)在[a,b]上存在直至n阶的连续导函数，在(a,b)内存在导数时，则对任意给定的x,x0∈[a,b]，至少存在一点ξ∈(a,b)，使得：

(3)

当x0=0时，泰勒公式就变成带有拉格朗日余项的麦克劳林公式(Lagrange)，即公式

(4)

1 泰勒公式的应用及技巧

如果函数f(x)是二阶或更高阶导数，且已知最高阶导数的大小或上下界，那么就可以利用泰勒公式证明不等式.使用泰勒公式证明的步骤一般分为两步，即(1)根据提供的已知条件，围绕需要证明的未知目标，选取合适的点将函数f(x)展成泰勒展开式；(2)结合已知条件，将泰勒展开式向着有利于证明目标不等式的方向进行适当处理，最终得到目标结果[5-6].胡春阳[7]将该证明过程细化为三步，就是在泰勒展开式基础上，选择等式两边的x与x0，然后对展开式进行扩大或缩小.

具体应用可以分别通过泰勒公式的两种形式，即带有佩亚诺型余项的泰勒公式和带有拉格朗日型余项的泰勒公式来简单证明一下.

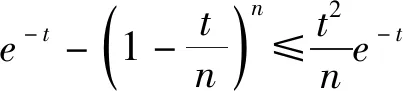
证明：不等式两边同乘e-t，利用带有佩亚诺型余项的麦克劳林公式进行展开，则

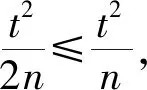
例2 设α>1，证明当x>-1时有不等式(1+x)α≥1+αx成立，且仅当x=0时等号成立.

证明：由于f(x)=(1+x)α在(-1,-)上二阶可导，且有f′(x)=α(1+x)α-1，f′(0)=α，

以及f″(x)=α(α-1)(1+x)α-2，

于是，对f(x)利用带有拉格朗日余项的泰勒公式展开可得

注意到上式最后一项是非负的，且仅当x=0时为0，所以(1+x)α≥1+αx(x>-1)成立，

且仅当x=0时等号成立.

例3 设f(x)在[0,+)上具有连续二阶导数，又设

f(0)>0,f′(0)<0,f″(x)<0,(x∈[0,+)).

证明：x∈[0,+)，由带有拉格朗日余项的麦克劳林公式有

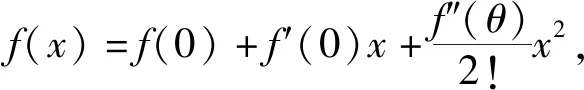
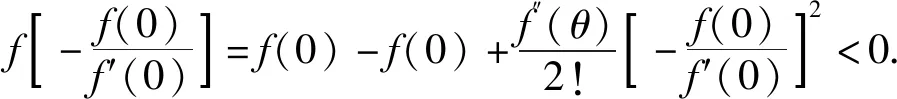
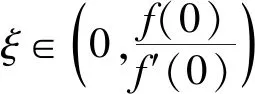
2 注意事项

通过以上实例可以看出，对于含有二阶或高阶导数的不等式，在利用泰勒公式证明时，一般需要注意以下两点：(1)函数需要展开到第几阶；(2)是采用佩亚诺余项，还是拉格朗日余项的泰勒公式[8].对于高阶导数的不等式，通常采用拉格朗日余项的泰勒公式[9].

由于在应用泰勒公式证明不等式过程中，需要对函数f(x)在点x0处进行泰勒展开，所以恰当地选择x0就成为证明过程的重点，通常选用区间的端点、中间点、函数的极值点、导数为零的点或信息给的比较多的点等特殊点作为x0[10].具体如何寻找这个特征点x0呢？石秀文[3]按照已知条件中有无特征点x0进行具体分析，强调具体问题具体分析，而且要熟练运用放缩技巧.

3 结 语

使用泰勒公式来证明高阶不等式，具有简便有效的特点.为了介绍泰勒公式在不等式中的应用，通过一些具体事例来进行分析说明.可是在证明过程中，会存在一些具体问题需要解决，应根据不同情况，采用不同的证明方法和步骤，并且要严格遵循相关注意事项.相信通过泰勒公式的介绍，已以及应用步骤和注意事项，会对高校学生学习高等数学有所帮助.