均值和方差变动的马科维茨投资组合模型研究

一、前言

近年来，随着我国证券市场的发展，越来越多的投资者开始购买股票、基金、期货期权等金融产品。随着投资者交易行为的增加和投资知识的积累，他们开始意识到购买金融产品，不能只关注收益，也要注重风险，要学会如何规避风险，实现投资者自身效益最大化。风险的规避需要投资者具备一定的投资组合理论。投资组合理论是由美国经济学家马科维茨提出的。马科维茨的投资组合理论假设可以用历史收益率的均值和方差代替未来的均值和方差。但是在现实中，收益率的均值和方差并不是一成不变的。传统的马科维茨投资组合理论没有考虑这种变化，这将导致传统的投资组合理论推导出的投资组合和现实中的最优投资组合存在偏差。因而研究均值和方差变化的马科维茨投资组合理论具有现实意义。本文旨在建立均值和方差变动的马科维茨投资组合模型，使传统的投资组合理论更加丰富。

二、文献综述

自从1952年马科维茨提出了均值-方差模型，许多学者开始研究均值-方差模型。何朝林等（2011）基于模型参数不确定性，构建了稳健静态资产组合模型；周圣（2012）发现在一定的限制条件下，无风险资产模型的有效前沿曲线和最初的均值-方差模型的有效前沿曲线是一致的。张群等（2013）把交易中的限制条件引入均值-方差模型，创建了风险偏好系数均值方差模型。姚海祥等（2013）考虑通货膨胀因素，推导出了均值-方差模型有效边界的表达式和有效的投资策略。Lam，Jaaman和Isa（2013）放宽了均值-方差模型中的正态假设条件，把概率分布的峰值和偏度加入均值-方差模型。

三、传统的马科维茨投资组合模型

传统的马科维茨投资组合模型有很多假设条件，假设投资者是理性的、所掌握的信息是一致的、了解金融产品的一切性质；假设金融产品收益率服从正态分布，每一种金融产品收益率相关；假设金融市场是完全竞争的。根据上述假设条件，马科维茨建立了投资组合的均值方差模型。假设在金融市场上存在N种证券（本文不研究无风险资产），每种证券收益率的均值用R表示。每种证券收益率的方差用v表示。用V表示N种证券收益率的协方差，即表示每一种证券购买一个单位所带来的风险。用W表示证券组合中每一种证券的投资比例。WTR表示证券投资组合的收益率，1/2WTVW表示证券投资组合的风险。传统的马科维茨均值方差模型是在收益固定的情况下，实现投资组合风险的最小化。即模型如下：

约束条件为

其中，Ep是期望收益率。

对模型进行求解，可以求出在收益率固定的情况下，所对应的最低风险。把收益率和该收益率所对应的最低风险描在坐标轴上，可以得出有效前沿曲线，该曲线上的点满足在收益率固定的情况下，风险最小；风险固定的情况下，收益率最大。根据上面的模型可以推导出有效前沿曲线的表达式如下：

四、均值和方差变动的马科维茨投资组合模型

马科维茨提出的投资组合模型假设每一种金融产品收益率的均值和方差都是固定不变的。然而在现实中，金融产品的收益率的均值和方差会同时发生变化，传统的马科维茨投资组合模型所推导出的有效前沿曲线不再适用，因此需要建立均值和方差同时变动的马科维茨投资组合模型，为投资者提供更准确的投资建议。

约束条件为

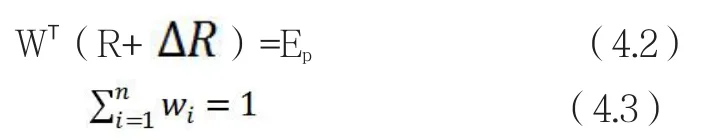
进行求解，可以求出有效前沿曲线，表达式如下：

由上文的有效前沿曲线可以看出，在资产收益率的均值和方差同时变动的情况下，有效前沿曲线的端点（）和弯曲程度都发生了变化。根据这个模型，投资者可以依据现实情况调整投资组合。

五、均值和方差变动的马科维茨投资组合模型应用分析

（一）样本选择及数据处理

本文选择了上证50指数成分股中的四只股票，它们分别是中信证券、中国人寿、中国联通、贵州茅台。之所以选择这四只股票是因为它们属于不同的行业，股票之间的相关程度比较低，充分满足投资组合分散性特征。

选取四只股票从2019年1月1日到2019年8月20日的日收盘价作为样本数据。对这些数据进行处理，分别求出每只股票的收益率以及收益率的均值和方差。本文所选取的数据来自国泰安CSMAR数据库。

由于本文所选取的数据是每只股票的日收盘价，因此还需要使用收益率公式计算每只股票的收益率。利用MATLAB软件处理收益率数据，可以得出股票收益率的均值、方差以及协方差。根据股票收益率均值和协方差矩阵，结合均值和方差不变的有效前沿曲线方程可以求出均值方差不变的有效前沿曲线函数表达式为，由该函数表达式可以看出，均值和方差不变的有效前沿曲线的端点为（），弯曲程度为。把均值和方差不变的有效前沿曲线画在坐标轴上，图形如下。

由该图形可以看出，投资者应该选择有效前沿曲线端点以上的点进行投资。随着风险的增加，收益增大。端点以下的点没有使投资者效用达到最大化。

（二）均值和方差变动对有效前沿曲线的影响

由于四只股票收益率均值和方差同时变化的有效前沿曲线方程复杂，因此本文只研究中信证券收益率均值和方差变化的有效前沿曲线，与中信证券收益率均值和方差不发生变化的有效前沿曲线比较，得出中信证券收益率均值和方差同时发生变化对有效前沿曲线的影响。

首先通过求出中信证券每月收益率的均值和方差证实中信证券每月收益率均值和方差同时发生变化。之后假设未来中信证券收益率均值增加0.001，方差随均值变动而变动，把变动的数据带入第三部分均值和方差同时发生变化的马科维茨投资组合模型中，可以得出中信证券收益率均值和方差变动的有效前沿曲线，该曲线函数表达式为，由该函数表达式可以看出，均值和方差变动的有效前沿曲线的端点为（），弯曲程度为，为了更好的观察均值变动0.001对有效前沿曲线的影响，本文把两种情形下的有效前沿曲线画在一个图形中。图形如下，蓝色曲线表示不变情形，红色曲线表示变动情形。由图形可以看出，均值和方差发生变动的有效前沿曲线的弯曲程度更大，对称轴更偏上，最小方差点更靠右。对于投资者来说，所面临的风险和收益更加具有不确定性。

六、结语

马科维茨提出的投资组合模型对资产收益率进行了严格的假设，假设收益率均值和方差是不变的，可以用过去的投资组合模型指导现阶段的资产配置。然而，在现实的投资活动中收益率均值和方差会同时变动。因此本文建立了均值和方差变动的马科维茨投资组合模型，得出了有效前沿曲线。把变动情形和不变情形的有效前沿曲线对比，可以得出，均值和方差的增大将会导致有效前沿曲线弯曲程度变大；对称轴向上移动；最小方差点向右移动。因此投资者在进行资产组合时，一定要关注收益率均值和方差变动对投资收益和风险的影响，降低投资的不确定性。