环戊二烯基锕系配合物结构和还原性质的密度泛函理论研究

杨俊杰, 马莉雯, 杨光露, 卜 赫, 郝璐祎, 郭元茹，* ，潘清江

(1. 东北林业大学 材料科学与工程学院, 哈尔滨 150040; 2. 黑龙江大学 化学化工与材料学院, 哈尔滨 150080)

0 引 言

锕系核素是生产核能和制造核工业产品的重要原料之一，其高效利用已为现代社会发展提供了重要能量来源。然而，产生的放射性废物处置是目前全球所面临的难题。了解并掌握锕系有机金属配合物的结构和基本化学性质至关重要。近年，锕系配位化学的快速发展得到了数目众多、结构确定的锕系配合物，这为其电子结构和反应性质的深入理解提供了重要参考[1]。上世纪五十年代中期，Reynolds和Wilkinson合成了第一个环戊二烯基四价铀配合物[Cp3UIVCl] (Cp=C5H5)[2]；Kanellakopulos B等[3]合成和表征了三价铀配合物[Cp3UIII]。由于环戊二烯基配体独特的电子与配位性质，使其能够稳定相对富电子的低价铀离子，目前它仍在低价铀配位化学领域占主导地位[4]。

由于铀具有5f36d17s2电子组态，可以形成从+II ～ +IV的各种氧化态。从2013年起，陆续得到几个晶体结构确认的+II铀配合物[5-6]。合成路线均采用还原+III母体配合物的方法，使得+III配合物氧还原性质研究显得迫切且必要。但这些低价铀配合物化学稳定性差、氧化还原实验研究中困难多，因此通过可靠理论计算探索它们结构和性质是目前的有效手段之一[7-10]。

本文将使用相对论密度泛函理论方法探索一系列环戊二烯基三价和四价铀配合物的几何和电子结构、化学键和电子自旋密度，重点考察了还原电势并阐明低价铀配合物的还原机制，为核燃料的开发利用和乏燃料/核废料的安全处理提供参考。

1 计算细节和理论方法

系统研究了三环戊二烯基配位铀的化合物，包括8个三价和四价配合物，[Cp3UmX]n(X=F, Cl, Br, I; m=III, n=-1; m=IV, n=0)。同时计算了[Cp3Um]n(m=III, n=0; m=IV, n=+1)；相较前面配合物，它相当于空置配位(Vacant)，文中标识为X=Vac；另外，变换金属中心，考虑了超铀配合物[Cp3Anm]n(An=Np, Pu)。

采用ADF2014程序[10]优化了配合物结构。基于此进行频率计算。结果未得到虚频，表明这些结构为势能面上极小值点。频率计算同时获得零点振动能、熵、自由能等热力学参数。考虑溶剂对配合物电化学性质的影响，运用COSMO模型模拟溶剂环境效应。计算中选用四氢呋喃(THF)作为溶剂，其介电常数为7.58。模型中运用Klamt半径(nm)，即U/Np/Pu=2.20、H=1.30、C=2.00、F =1.76、Cl=2.05、Br=2.22和I=2.38。计算中使用标量相对论ZORA哈密顿、GGA-PBE泛函和Slater-TZP基组。对An采用冻结1s-4f轨道近似，而C和F冻结1s轨道、Cl采用冻结1s-2p、Br采用冻结1s-3p和I采用冻结1s-4p。还采用ADF程序进行了QTAIM (Quantum Theory of Atoms-in-Molecule)计算，得到在U-X键临界点(Bond Critical Point, BCP)的电子密度ρ(r)和拉普拉斯密度▽2ρ(r)。

在ADF优化结构基础上进行了Gaussian09计算[11]，运用Multiwfn软件分析得到除ρ(r)和▽2ρ(r)之外的能量密度H(r)、离域化指数δ(U, X)和椭球率ε。Gaussian计算中采用GGA-PBE泛函方法和混合型基组。对U原子使用Stuttgart准相对论效应的小核赝势，对核内的60个电子进行冻结近似、对其外层32个电子采用相应的基组进行全电子计算；Cl、Br和I使用Hay和Walt的准相对论LANL08d小核赝势和相应基组；采用6-31G(d,p)基组处理其它原子。

2 结果与讨论

2.1 几何结构

考虑到电子在轨道中的各种占据状态，三价和四价铀配合物可能具有多种电子自旋态异构体。例如，结构优化表明三价配合物可具有二重态和四重态。比较它们的总能(E)和相关热力学函数(E0, H, G)发现四重态异构体的能量最低，对应于基态结构。同样，四价铀配合物的计算表明其电子自旋三重态为基态，重点探讨基态配合物的结构和各种性质。

配合物的结构见图1，优化得到的几何结构参数和键级见表1中。由表1可见，An-C的距离为0.272～0.281 nm。环戊二烯配体上C-H和C-C的平均距离分别为0.109 nm和0.142 nm。An-Cpcent的距离在0.243～0.251 nm。优化的U-X距离随着F、Cl、Br、I逐渐增长，这主要与卤素原子半径有关。

图1 配合物[Cp3UmX]n结构(X=F, Cl, Br, I; m=III, n=-1; m=IV, n=0)和[Cp3Anm]n(An=U, Np, Pu; m=III, n=0; m=IV, n=+1)Fig.1 Structures of complexes[Cp3UmX]n

表1 优化的配合物几何参数和键级(括号中)，以及相应的实验值a(键长单位为nm、键角单位为°)

优化的配合物[Cp3UmX]n(X=F, Cl, Br, I, Vac.; m=III, IV)的U-C和U-Ccent距离见图2，相同氧化态时，无论是三价还是四价配合物的U-C和U-Cpcent键长随着X=F、Cl、Br、I逐渐变短。由于X对金属中心配位作用越弱，铀上的价电子则分布于U-X之间的更少，从而导致U和Cp之间的价电子增多、作用增强，其距离因而更短。对于[Cp3Um]n没有X配位的极限情况，价电子则完全分布于U和Cp之间，所以该配合物具有最短的U-C/Cpcent距离。由图2可见，中心金属氧化态(III和IV)对U-C/Cpcent距离有一定的影响。三价的稍长0.001～0.004 nm。这一计算结果规律性一方面与实验值相一致；另一方面与UIII离子半径长于UIV的相符合。

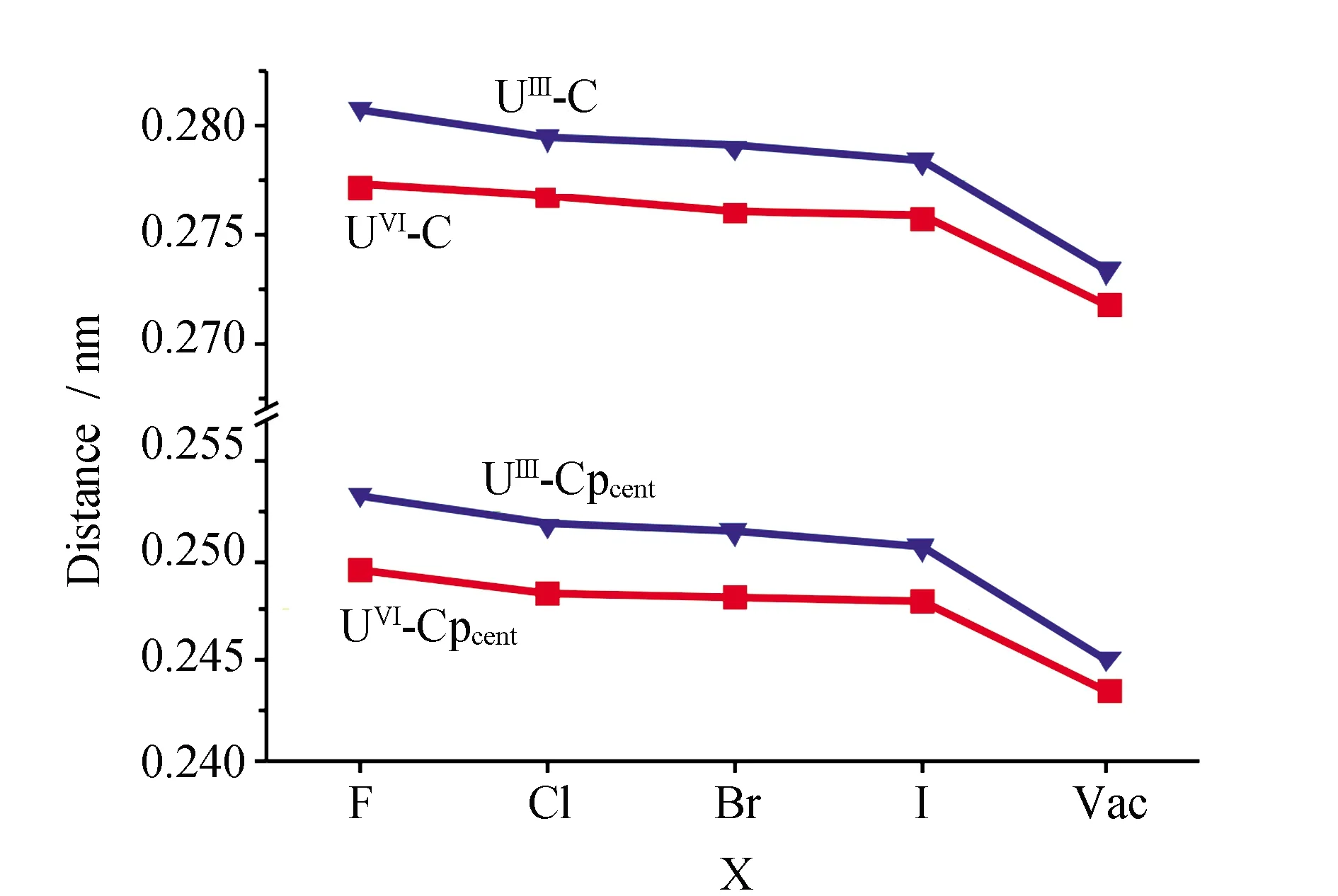
图2 优化的配合物[Cp3UmX]n的U-C和U-Ccent距离Fig.2 Optimized U-C and U-Ccent bond lengths (nm) of [Cp3UmX]n

从键级值分析可见，An-C (An=U、Np、Pu)的键级在0.3左右，具有较弱的单键性质。而计算的U-X键级则在0.59～1.27，表明U与X之间形成配位单键，此QTAIM拓扑分析中进一步证实。

2.2 QTAIM分析

使用原子在分子中的量子理论(QTAIM)分析了U-X的化学键类型和强度。相关参数包括电子密度ρ(r)、拉普拉斯密度▽2ρ(r)、能量密度H(r)、离域化指数δ(U, X)和椭球率ε。分析中可观察到U-X间存在红色小球，这就是U-X键的临界点(Bond Critical Point, BCP)，表明中心铀离子与配体X间存在相互作用。由于ADF程序计算只能得到ρ(r)和▽2ρ(r)，使用了Gausssian09和Multiwfn，分析得到更多参数。比较可见，使用ADF与Gaussian计算得到的ρ(r)与▽2ρ(r)值非常接近，下面将重点分析Gaussian的结果。

如表2所示，除U-F的ρ(r)数值>0.1而<0.2，其它的U-X的ρ(r)值均<0.1而>0；并且所有配合物的H(r)<0，而▽2ρ(r)>0。δ(U, X)是一种键级的衡量标准，数值在0.52～0.86；将其与表1中计算的U-X键级对比，数值略小但变化趋势基本一致。另外，计算的所有配合物的椭球率ε数值均接近于零，表明U-X的单键特征。对三价铀配合物，有文献报道了在U-Cl和U-I临界点的电子密度ρ和离域化指数δ的计算值。如，U-Cl键的ρ和δ分别为0.064和0.600，而U-I键的分别为0.039和0.542，与计算结果非常接近。综合分析QTAIM数据并结合以往研究得到的结论[7-8]，配合物[Cp3UmX]n(X=F, Cl, Br, I; m=III, IV)中的U-X为典型的配位键且是单键性质。

表2 计算配合物在U-X键临界点的QTAIM参数a、离域指数δ(U, X)和椭球率ε

2.3 电子结构

为理解低价铀配合物在氧化还原过程中几何结构和U-X键的变化，下面将对配合物进行电子结构分析。计算考察了在THF溶液条件下配合物基态的轨道成分和性质。以配合物[Cp3UIVCl]为例，LUMO+1 (L+1)到HOMO-1 (H-1)轨道主要为U(5f)成分，同时有较少的U(6d)和微量的U(7s)贡献。2个U(5f)成分高能占据单电子轨道(HOMO和H-1)表明配合物具有四价中心铀离子，具有5f2电子组态。基态为三重电子态。在最高占据轨道HOMO中，还有2.1%环戊二烯基配体Cp的参与。从HOMO到H-6，配体Cp的轨道贡献逐渐变大，由1.1%增加到77.2%。另外，H-3轨道中还出现配体Cl的轨道成分，占12.6%。

[Cp3UIVCl]单电子还原可生成配合物[Cp3UIIICl]-。分析轨道成分发现前线分子轨道L+1～H-2以U(5f)和配体性质为主导(表3)。在HOMO到H-2中，U的成分超过86%，其中U(5f)超过80%，同时伴有少量的U(6d)贡献，小于5.5%。这3个金属成分轨道有3个自旋平行的电子占据。这与配合物三价铀中心具有5f3电子组态指认相一致。从HOMO能级开始出现环戊二烯基配体轨道成分，而H-3到H-6则以Cp成分为主，贡献均高于70.9%。UIII配合物的分子轨道图与态密度见图3，包括8个高占据轨道HOMO～H-7和3个空的LUMO～L+2轨道。此为上述指认提供了更为直观的参考。

表3 配合物[Cp3UIIICl]-的部分α自旋轨道成分

图3 配合物[Cp3UIIICl]-的部分α-自旋轨道(左侧)以及态密度(右侧)Fig.3 Diagrams of selected α-spin orbitals of [Cp3UIIICl]- (left) and density of states (right)

无论是三价还是四价铀配合物，当X从F变换到I时，前线分子轨道的能量逐渐降低。电子结构详细分析表明，四价和三价铀配合物分别具有2和3个U(5f)性质的高能的单电子占据轨道；它们的中心离子分别具有5f2到5f3电子组态。电子结构反映单子还原反应发生在金属中心，Cp有少量参与，X的参与很少。这将被下面的电子自旋密度分析所证实。

2.4 还原电势与机制

为探索铀配合物氧化还原机制，计算了配合物中各个部分的电子自旋密度，标记为SFrag。对于三价铀配合物[Cp3UIIIX]-，中心铀的电子自旋密度的理论期望值为3.0，而实际计算的SU值均略<3.0，数值为2.85～2.91。计算的SX均约为-0.03，S3Cp数值为0.11～0.19。说明中心铀离子和卤离子配体上的很小部分α-自旋电子转移到环戊二烯配体上。在配合物[Cp3UIVX]中，计算的SU值均>理论期望值2.0。另外，计算的[Cp3AnIII]-/[Cp3AnIV] (An=U, Np, Pu)的SAn分别为2.89/2.15、4.15/3.51和5.29/4.77，与相应的期望值相当，其中Pu和NpIV的数值偏差相对较多。

变换X的铀配合物在不同氧化态时的电子自选密度差值(ΔSFrag)见图4，对应了还原过程中体系电子转移情况。可观察到，电子还原主要发生在金属铀部分，ΔSU数值为0.70到0.74；ΔSCp数值为0.25～0.29；ΔSX贡献较小，≤0.05。因此，指认单电子还原主要发生在金属中心部分，伴有一些Cp配体的参与，而X配体的贡献很少。

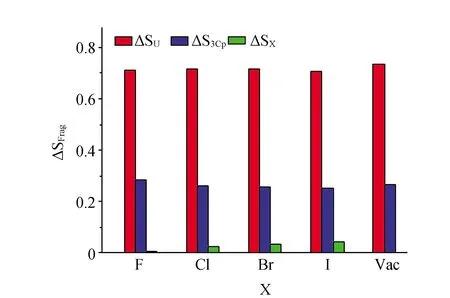
图4 铀配合物还原时每个片段电子自旋密度变化值(ΔSFrag)Fig.4 Difference of electron-spin density of each fragment (ΔSFrag) of uranium couples in the reducing process

计算锕系配合物的单电子反应能见表4。借助计算得到配合物在气态条件下、溶液中以及考虑旋-轨耦合校正的反应自由能(ΔrG、ΔrG(sol)和ΔrG(sol-so))，以Fc/Fc+做参比电极，计算得到还原电势(E0，单位为V)为

式中:F为法拉第常数，其数值为96 485 C·mol-1。计算的参比电极在溶液中反应自由能G(sol)为-5.39 eV，考虑到旋-轨耦合影响时自由能G(sol-so)为-4.90 eV。

表4 计算的单电子还原反应能(eV)以及在THF中的还原电势E0(V)

在考虑溶液环境和旋-轨耦合校正条件下，计算的所有配合物的还原电势值均为负值。随着X=F、Cl、Br、I、Vac.变化，其还原电势逐渐增大(图5a)。计算的E0(sol)由-2.70 V增加到-1.19 V，而E0(sol-so)由-2.00 V增加到-0.63 V。同时考虑溶剂化效应和旋-轨耦合的E0(sol-so)比E0(sol)数值更正，且在实验值范围内[4]。这表明计算中考虑旋-轨耦合校正能的重要性。在THF溶液中以二茂铁作为参比电极，实验测试的[(C5Me5)2UCl2]-、[(C5Me)2UIIICl(THF)]、[(2,6-tBu2C6H3O)3UIII]、{[(Me3Si)2N]3UIII}和[(C5Me)2UIIICl2]-的单电子氧化电势分别为1.20、1.05、1.22、1.24和1.55 V[4]。实验与理论之间的偏差主要是由于配合物中的配体不同所引起的。文献[4]证明，三价铀配合物的氧化还原电势测量电受金属周围配体类型和数目的影响较大，同时溶液的配位属性也是测量准确性的关键问题之一。比较图2和图5(a)，可发现还原电势趋势变化与U和Cp之间作用强度密切相关，即U和Cp之间作用越强(U-C/Cpcent距离越短)，相应的E0值越正。U-C/Cpcent距离可以从结构优化中得到，而还原电势无论是计算还是实验均难以获得。因此，运用上面的规律性可以通过结构优化参数的方法预测氧化还原电势。这极大地简化和降低了实验难度。

在溶剂化效应下，随着An=U、Np、Pu变化，[Cp3AnIV]++ e=[Cp3AnIII]反应的自由能ΔrG(sol)分别为-4.20、-4.16和-4.91 eV。当考虑到旋-轨耦合影响时，自由能ΔrG(sol-so)的范围为-4.83 ～ -4.27 eV。计算发现，旋-轨耦合效应对单电子还原反应的贡献分别为-0.08、-0.24和0.08 eV。通过计算得到[Cp3AnIV]/[Cp3AnIII] (An=U、Np、Pu)的还原电势E0(sol)分别为-1.19、-1.23、-0.48 V。当考虑到旋-轨耦合影响时E0(sol-so)为-0.63、-0.50、-0.07 V。值得指出的是，还原电势E0(sol-so)从U到Np到Pu依次增大(图5(b))，这与实验测得An4+/An3+离子还原电势数值变化趋势相一致[12]，而E0(sol)中Np的数值最小。这再次强调引入旋-轨耦合校正的重要性。

图5 计算的配合物在THF中相对参比电极Fc+/Fc的还原电势(E0, V)Fig.5 Calculated reduction potentials (E0 in V) relative to the reference electrode Fc+/Fc in THF

3 结 论

使用相对论广义梯度密度泛函理论探索了[Cp3UmX]n(X=F, Cl, Br, I; m=III, n=-1; m=IV, n=0)的结构、电子自旋密度、U-X键性质和氧化还原行为，并与[Cp3Anm]n(m=III, n=0; m=IV, n=+1)进行了比较。

对可能存在的电子自旋态异构体优化表明，三价铀配合物具有三重态基态，而四价配合物的四重态为基态。计算发现中心金属氧化态对U-C和U-Cpcent距离有一定影响，其中三价配合物的稍长0.001～0.004 nm。这一计算结果与UIII离子半径长于UIV的相一致，同时还与报道的实验值相符合。基于电子密度的QTAIM拓扑分析表明U-X为配位化学键、单键本质。四价铀配合物的HOMO和H-1轨道为U(5f)性质，而三价铀具有3个U(5f)性质的高能的单电子占据轨道(HOMO～H-2)；电子结构表明它们的中心金属离子分别具有5f2到5f3电子组态。

电子结构计算显示单子还原反应主要发生在金属中心，Cp有少量参与，X的参与很少。这与电子自旋密度分析相一致。因而指认单电子还原为金属铀主导、Cp配体参与的反应机制。随着X=F、Cl、Br、I、Vac.变化，计算得到配合物的还原电势E0(sol)和E0(sol-so)均逐渐变小；建立了E0与U和Cp相互作用强度的正相关性。计算的E0(sol-so)比E0(sol)更正，且数值在报道的实验值范围内，表明考虑自旋-轨道耦合校正的重要性。计算的[Cp3Anm]n的E0(sol-so)值随U、Np、Pu依次增大，与实验测得的An4+/An3+离子的还原电势值趋相一致。

本文计算能为配体调控低价锕系有机金属配合物的电子结构、化学键性质和氧化还原行为提供理论支持，并为合成新型低价锕系金属配合物提供理论参考。