面积比对前可变面积涵道引射器性能影响的数值研究

2020-03-24胡文兵肖双强岳定阳

燃气涡轮试验与研究 2020年6期

陈佳，胡文兵，肖双强，伍鑫，岳定阳

(中国航发四川燃气涡轮研究院，成都 610500)

1 引言

变循环发动机具有宽广的工作范围、高单位推力及低油耗等特点，受到国内外科研人员及研究机构的重视。变循环本身要求发动机具有多个热力循环方案，通过发动机涵道比、增压比、涡轮前温度以及流量等循环参数的变化，实现最优的热力循环状态[1-2]。双涵道变循环发动机通过变几何机构的调节可以达到上述多个热力循环要求，被认为是未来最有希望的高性能动力方案。前可变面积涵道引射器(FVABI)是实现双涵道变循环发动机热力循环模式改变的一个重要部件，可改变核心流道及外涵道的气流流量分配。通过调节FVABI面积开关度来改变发动机涵道比[3-5]，与其他可调部件相配合，可使发动机具有大涵道比下低油耗和小涵道比下高单位推力的双重优势。

早在上世纪60年代国外就开始了变循环发动机的研究，并取得一定成果[6]。其中最具有代表性的变循环发动机为GE公司提出的具有双外涵变循环概念的F120发动机，也是第一台经飞行试验验证的变循环发动机[7-9]。1971年美国验证了双涵道变循环发动机，较于G4/J5涡喷发动机，其超声速巡航耗油率下降10%，亚声速耗油率改善达到24%[10]。国内变循环发动机研究起步较晚，刘增文等[11]在常规双轴涡扇发动机性能模拟程序基础上，添加了模式选择阀(MSV)、FVABI等部件模块，进行了变循环发动机的数值计算。其研究表明，与设计参数相同的常规涡扇发动机相比，变循环发动机模态转换方案可行，可有效提高发动机在部分推力时的空气流量，其耗油率明显降低。刘洪波等[12]以一涡扇发动机总体结构为基础，设计了模式转换及结构方案，对FVABI进行了运动仿真及有限元分析，从结构运动与强度方面确定了变循环方案的可行性。张荣等[13]基于涡扇发动机平台，制定了变循环发动机的调节方式，并对亚声速巡航与超声速巡航两种典型工况之间转换过程进行了数值仿真，结果表明所提出的调节方式能实现涡喷与涡扇工作模式的平稳转换。王靖宇等[14]通过比较基准圆筒型调节与带波瓣型调节机构的混合器性能，发现波瓣结构混合器总压损失小、外涵流通能力增强，但其密封结构复杂；同时还给出了特征涡对混合效率的影响规律。根据国内外公开报道，针对变循环发动机的研究主要集中在整机初步性能模拟计算、总体结构方案设计以及波瓣混合器研发，对于MSV及直推式FVABI等可调部件的气动与试验研究则较少，尤其缺乏对直推式FVABI引射特性及掺混过程机理性研究。因此，开展直推式FVABI气动机理研究是一项很有意义和前瞻性的工作，有望为变循环发动机可调部件的发展提供理论基础和知识储备。

本文采用三维数值模拟方法，在不同进口压比条件下，研究了面积比对FVABI流动损失、引射性能及掺混流场结构的影响，可为后续变循环发动机可调部件设计和改进提供理论参考。

2 数值研究

2.1 计算模型及网格结构

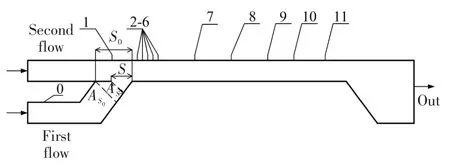
图1 FVABI试验几何模型Fig.1 Experimental geometry model of FVABI

图1为FVABI试验几何模型示意图。模型总长度L约2 m，由导流环、内涵进气机匣、内涵进气锥段、外涵支撑机匣、混合段机匣、后支撑机匣、排气锥、排气机匣及作动筒相关调节机构等组成。图中：S、S0分别为FVABI可变面积调节阀的开度和最大开度分别为垂直气流方向的可变和最大有效流通面积。0表示主流进口处壁面静压测点，1～11表示混合段外涵机匣外壁面静压测点；First flow与Second flow分别表示内、外涵通道，对应FVABI计算模型的主、次流；Out表示FVABI主、次流混合流道出口。通过调节开度改变AS大小控制外涵流量可实现涵道比的调节，下文采用面积比表示FVABI面积开度调节。

针对轴对称FVABI，取1/4几何模型进行三维数值模拟。网格划分采用ICEM分块方法，全部为结构化网格。近壁面附近对网格加密处理，使y+值满足湍流模型的要求。由于混合段剪切层内速度梯度较大，对混合段网格进行局部加密处理。经网格无关性验证，最终确定FVABI模型计算网格数量约为320万，计算区域及网格分布见图2。图中，pts、Tts分别表示次流进口总压、总温；ptp、Ttp分别表示主流进口总压、总温；pb表示主、次流混合段出口背压。

图2 CFD数值模拟网格Fig.2 CFD simulation grid

2.2 边界条件设置

次流与主流进口分别对应风扇、核心机驱动风扇(CDFS)出口，计算域进口采用压力进口边界条件，给定进口总温、总压；计算域出口采用压力出口边界条件，给定出口平均静压。所有壁面为无滑移、绝热固壁边界条件，周向设置为旋转周期性边界条件。计算工况为：给定背压pb/pts为0.93；进口压比ptp/pts为1.5、1.3和1.2；面积比为0.20、0.40、0.56、0.80及1.00。pts给定为当地大气压，表1给出了具体的边界条件设置。

表1 边界条件设置Table 1 Boundary condition setting

2.3 湍流模型及验证

图3 外涵壁面静压分布数值模拟结果与试验值的对比Fig.3 Comparison of static pressure distribution between experiment and simulation

3 结果分析

3.1 FVABI流动损失分析

FVABI产生的气流总压损失将直接影响发动机的最终性能。为此，在保证流量的条件下对其总压损失及变化规律进行研究。本文总压恢复系数采用截面质量平均总压参数计算，其具体定义为：

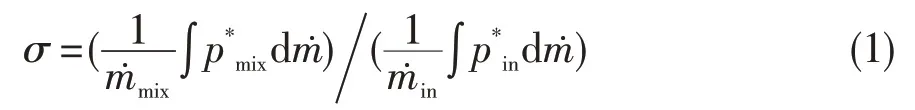
式中：σ为FVABI总压恢复系数，分别表示混合段主、次混合流量和混合总压，表示进口折合流量，p*in表示主、次流进口总压。图4给出了不同进口压比下FVABI出口总压恢复系数随面积比的变化规律。从图中可知，当面积比不变时，出口总压恢复系数随进口压比的增大而减小。这是由于FVABI总压损失主要由掺混损失和摩擦损失组成，当进口压比增大，进口速度与混合速度差值增大，使得掺混损失和摩擦损失增加所致。此外，进口压比1.3与1.5之间的总压恢复系数变化量Δσ约为进口压比1.2与1.3之间的2倍，表明出口总压恢复系数与进口压比成线性变化关系。当进口压比不变时，出口总压恢复系数随面积比增大而逐渐减小，这主要是因为面积调节阀门打开，主流的高能流体增加，掺混损失增大所致。实际变循环过程中，同一背压条件下，改变面积比代表了发动机涵道比的变化。不同进口压比下，FVABI调节阀门全开时存在最小总压恢复系数。

图4 FVABI出口总压恢复系数随面积比的变化Fig.4 Total pressure recovery coefficient of FVABI with different area ratio

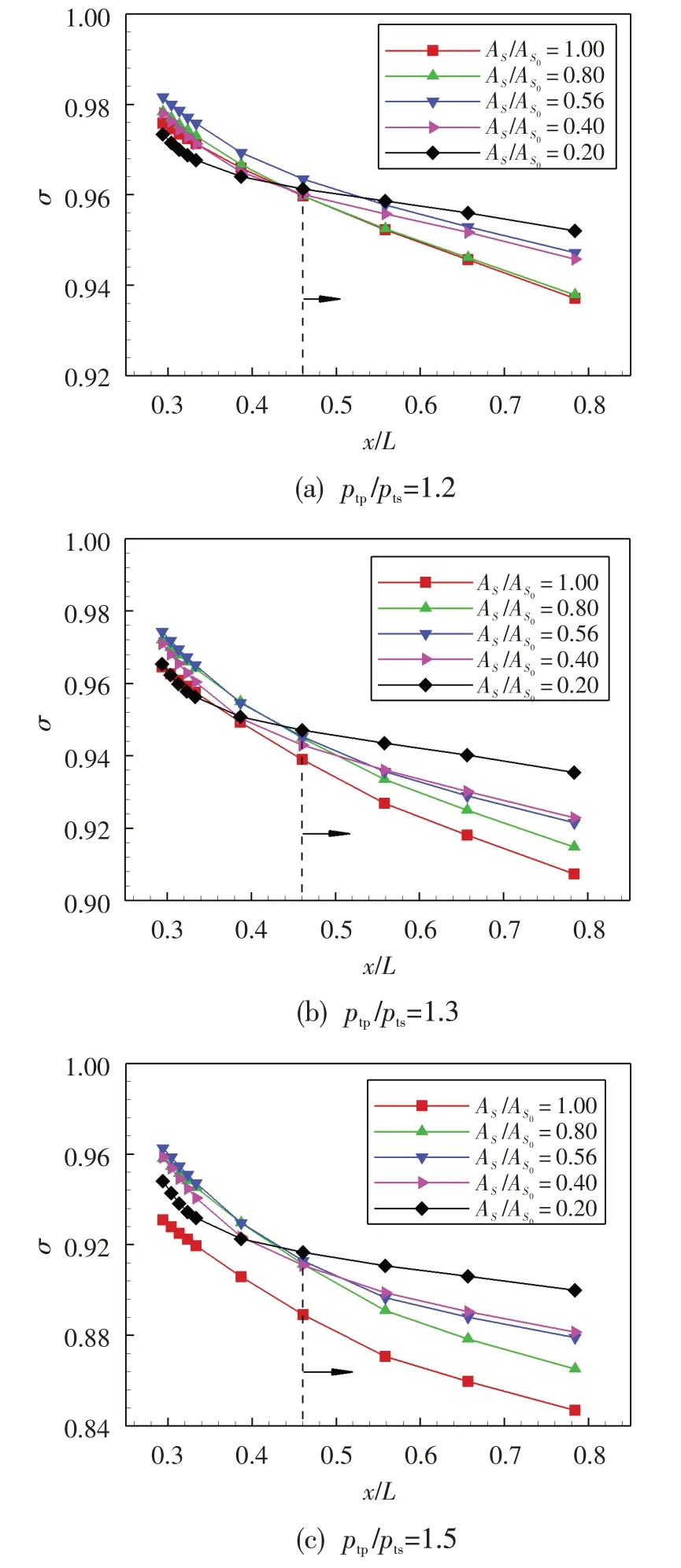
图5 不同面积比沿顺气流方向各截面总压恢复系数的变化(pb/pts=0.93)Fig.5 Total pressure recovery coefficient along flowing cross plane under different area ratio

图5给出了背压0.93时，不同进口压比条件下FVABI顺气流方向不同截面处的总压恢复系数随面积比的变化。可见，顺气流方向各截面处总压恢复系数逐渐减小，但减小的速率逐渐变缓。由于在掺混初始阶段主、次流速度差最大，主、次流动量交换过程中能量耗散较快，导致在初始掺混过程中总压恢复系数下降较快；但在黏性力作用下，主、次流速度差逐渐减小，掺混逐渐均匀，气流总能量耗散相对减缓，使得顺气流方向各截面总压损失增加的速率有所降低，总压损失系数下降平缓。此外，由图还可看出，进口压比越低总压恢复系数越大，且顺气流方向变化平缓。掺混截面x/L=0.28～0.46之间为主要掺混区域，总压损失急剧增加，且进口压比越大顺气流方向总压恢复系数曲线斜率越大。当截面位置x L大于0.46后，沿顺气流方向的总压恢复系数与面积比成反比。这是由于面积比越小主流进入外涵的空气流量越少，掺混损失降低，截面总压恢复系数增大。当进口压比为1.2时，面积比0.80与1.00相比，沿程总压恢复系数变化曲线基本重合；当进口压比不同时，面积比0.40与0.56相比，同样存在这种现象。这表明在一定面积比范围内，总压恢复系数对面积比变化敏感度较低。

3.2 FVABI引射性能分析

图6、图7分别示出了不同进口压比时主、次流流量随面积比的变化。可看出，主流流量随面积比增大而增加；进口压比越大主流流量曲线斜率越大；面积比增加，不同进口压比之间的流量差值增大。次流流量随面积比增大而减少，且面积比减小时次流流量曲线斜率逐渐减小。进口压比为1.5时，面积比从0.40减小到0.20过程中，次流流量基本保持不变，但主流流量持续减少。这表明随着面积比减小，次流达到扼流状态，而进口压比越大达到扼流状态时相应的面积比越大。

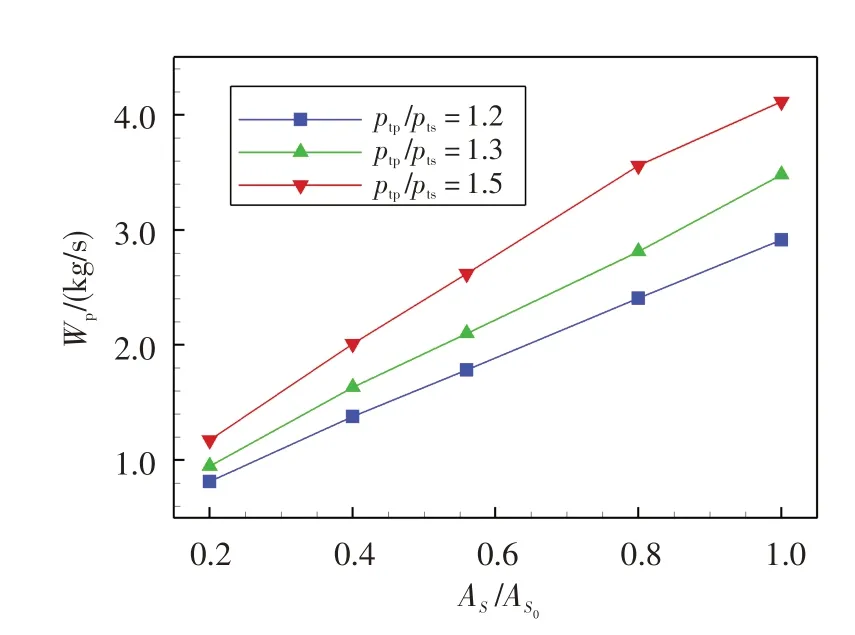
图6 主流流量随面积比的变化Fig.6 Main flow mass with different area ratio

图7 次流流量随面积比的变化Fig.7 Secondary flow mass with different area ratio

引射系数B是评估FVABI引射能力的主要参数，决定了变循环发动机涵道比的变化特性。图8示出了不同进口压比下FVABI引射系数随面积比的变化。如图所示，随面积比增大，不同进口压比下引射系数均减小。这是由于面积比增大，主流流量增加，次流流量减小，面积比越小，进口压比对引射能力的影响越大。在相同面积比下，进口压比越小，引射系数越大，主流对次流的引射作用越强。

图8 FVABI引射系数随面积比的变化Fig.8 Ejector coefficient of FVABI with different area ratio

3.3 FVABI计算流场分析

图9给出了进口压比1.3时，不同面积比下顺气流方向流道外壁面的静压分布。在掺混段进口处，主流将压力能转化为动能，主流静压低于次流总压，次流入口段气流受到抽吸作用速度增加，壁面静压急剧减小；随着面积比减小，主流高能流体流量减少，动量交换带动次流加速性减弱，对应掺混中心位置处静压升高，如图中=0.30处静压随面积比变化所示。进入掺混段后，主、次流之间在黏性力作用下进行能量、动量及质量掺混，气流掺混后速度趋于均匀，压力能逐渐恢复，使得混合区域静压逐步提升。面积比越小恢复到稳定静压的距离越短，面积比为0.20时在=0.48处静压已恢复。此外，由于出口处存在支撑板，使得流通面积减小，气流速度增大，静压略有降低。

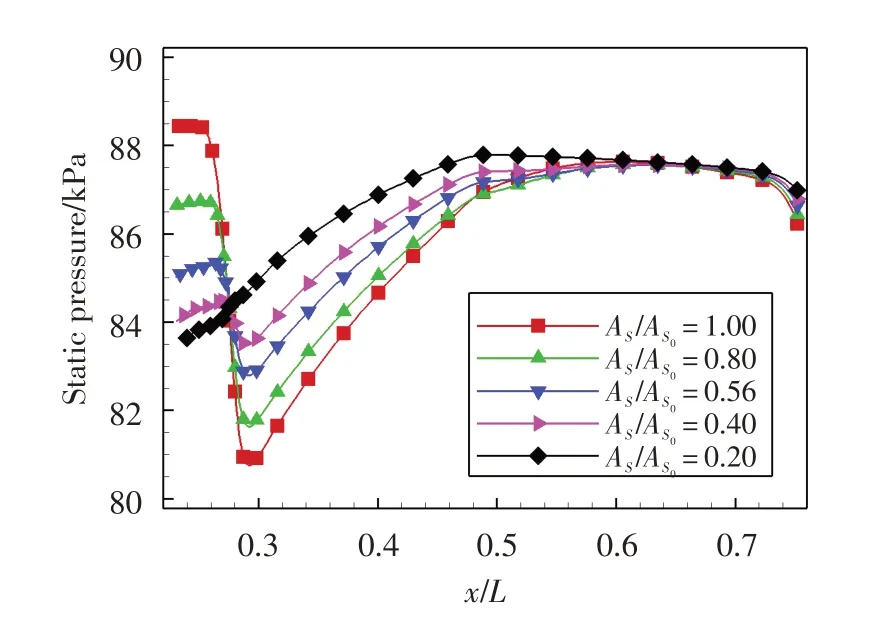
图9 不同面积比下顺气流方向流道外壁面的静压分布(ptp/pts=1.3)Fig.9 Static pressure distribution along flowing cross plane under different area ratio

图10 不同面积比下顺流向各截面的马赫数云图(pb/pts=0.93，ptp/pts=1.3)Fig.10 Mach number distribution along flowing cross plane under different area ratio

图10示出了背压0.93、进口压比1.3时，不同面积比下顺气流方向各截面的马赫数分布。从图中可看出，面积比越大收缩型主流道速度越大，可调阀门全开时主流道最大马赫数为0.86；随着阀门关闭面积比减小，主流流量减少、速度降低。在主、次流掺混位置之前，随面积比减小，次流速度增加；在主、次流掺混位置后，随面积比减小，次流速度减小。主、次流在掺混段存在明显的速度掺混界面，面积比减小过程中，速度掺混界面越小、越靠近流道内壁，掺混影响区域也逐渐减小，马赫数在掺混作用下恢复均匀速度较快，速度掺混界面逐渐消失。因此，调节过程中，面积比减小，出口总压恢复系数逐渐增加，与图4中所示结果一致。

图11 不同面积比下掺混段速度沿径向分布曲线(ptp/pts=1.3)Fig.11 Radial distribution of velocity under different area ratio at mixing section

图11示出了进口压比1.3，面积比0.20、0.56及1.00时，顺气流方向x/L=0.27截面处的速度径向分布。图中：h为掺混流道沿径向总高度，r为任意掺混流道高度位置，虚线之间为掺混层厚度。不同面积比下，在掺混段靠近主流出口处，由于压力能转换为动能，速度急剧增加；流体黏性作用使快层流体团进入慢层传递动量使得慢层加速，反之慢层流体团阻滞使得快层减速。随着主、次流在掺混段混合，主流将能量沿径向传递给次流，使掺混层上部次流逐渐趋于均匀流动，面积比分别为1.00、0.56、0.20时，掺混层厚度相应为0.16h、0.10h、0.08h，逐渐减小；同时，掺混下边界靠近内流道壁面，与壁面距离由0.30h减小到0.07h，符合图10马赫数云图中主、次流沿顺气流方向掺混的变化趋势。据此可得出，面积比对掺混层位置及掺混区域大小存在很大影响。