内柱孔和内锥孔圆柱形变幅杆

2020-03-23贺西平王照伟

声学技术 2020年1期

张然，贺西平，王照伟

(陕西师范大学物理学与信息技术学院，陕西省超声重点实验室，陕西西安710119)

0 引言

超声振动系统对于超声加工而言是不可或缺的。超声振动系统一般由超声换能器，超声变幅杆及加工工具头组成。变幅杆在振动系统中的主要作用是聚集超声振动能量，将机械振动的质点位移或速度放大，还可以作为机械阻抗变换器在换能器和声负载之间进行阻抗匹配[1]。近年来，随着超声技术在各个领域的广泛应用，人们对超声变幅杆的关注度也越来越高。许多学者在变幅杆研究方面取得了进展。Makuta 等[2]提出使用钛合金制成的中空阶梯形变幅杆来放大超声波振动，很容易产生直径小于100 µm 的微泡。王维鸽等[3]以设计大放大系数、高能量转换效率的变幅杆为目标，研究了内通孔分别为柱孔和锥孔而外形为锥形的变幅杆，并计算了杆中应力以及振动位移的分布规律。张云电等[4]设计了带中心通孔的夹心式压电换能器和圆锥变幅杆，用于超声珩磨的超声振动系统。加工陶瓷等易碎材料时，利用超声振动的带孔变幅杆的设备比起传统的利用激光和水射流的设备更简易和小型化[5-6]。孔型变幅杆还可将鸡蛋壳的宽端打孔加工为圆形来提取可预防疾病的疫苗，克服了传统方法即用金属刀片切割器处理时会产生大噪声且切割面粗糙、效率低等问题[7]。超声加工装置和抛光浆联合可用于玻璃等易碎材料的加工孔领域[8-9]；超声椭圆振动套磨制孔技术可用于航空航天领域[10]；超声加工还可用于超声辅助珩磨和超声辅助钻削加工等领域[11]。

本文提出了中心孔分别为柱形和锥形的圆柱形变幅杆。基于解析法推导了这两种孔型变幅杆的频率方程及性能参数表达式，利用有限元法计算了在谐振状态下这两种变幅杆的应力及振动位移沿轴向分布的规律。结果表明，柱形孔的深度为1/4波长时，放大系数只与横截面积之比有关。在相同谐振频率及面积系数下，锥形孔变幅杆的放大系数小于柱形孔变幅杆的放大系数大，但其应力曲线光滑且应力极大值较小。

1 频率方程、放大系数的推导

图1(a)、1(b)分别是带有柱形孔、锥形孔、外形均为圆柱形的半波长变幅杆，编号为1#和2#。如图1 所示，以输入端圆心为坐标原点建立直线坐标系。1#中的S1、L1、S2和L2分别为实心部分与柱形孔的横截面积与长度，实心端的半径为R，柱形孔的孔半径为R1，则S1=πR2， S2=π( R2−)，其中ξ1和2ξ 分别为输入端与输出端的纵向振动位移；2#中的1S′、S2′、3S′、a 和b 分别为实心部分与锥形孔两端的横截面积与其对应的长度，设实心端的半径为R，锥形孔小端半径为，孔大端半径为，则S1′=πR2，S2′=π( R2−R)，S3′=π(R2−)，其中和2ξ′分别为输入端与输出端的纵向振动位移。图1(c)为陶瓷等易碎材料(图中用矩形表示加工对象的截面，加工对象当然也可以为其他形状)被两种变幅杆打孔后的效果图，打孔的半径为R。变幅杆的材料取 45#钢，密度为 7 800 kg·m-3, 弹性模量为2.09×1011N·m-2,泊松比为0.28。外径R 取26 mm，R1与取21 mm，取18 mm。

1.1 柱形孔变幅杆

中心孔为圆柱形的变幅杆的位移函数可表达为

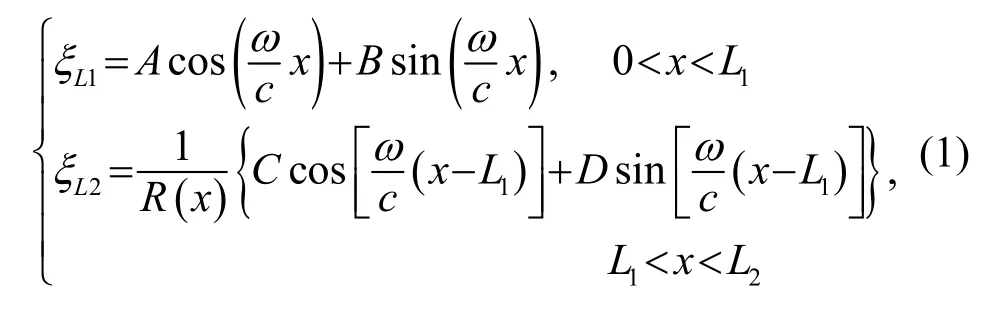
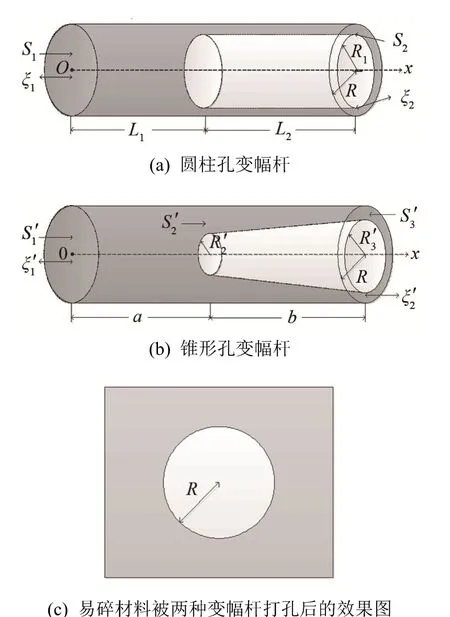
图1 两种孔型变幅杆及易碎材料被打孔后的示意图Fig.1 Schematic diagrams of two horns and the punched fragile material

其中：R (x ) = R − R1；面积系数。两端自由边界条件为

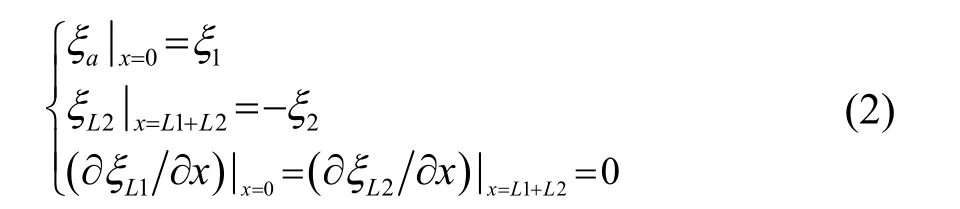
实空两部分连接处的连续性条件为

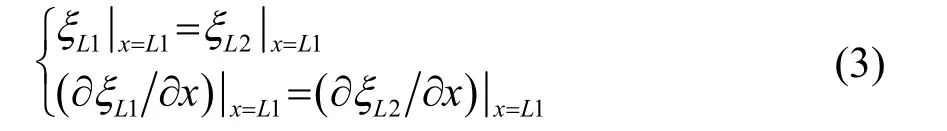
由式(2)、(3)确定常数A、B、C 和D，代入式(1)，得到位移表达式：

频率方程和放大系数分别为

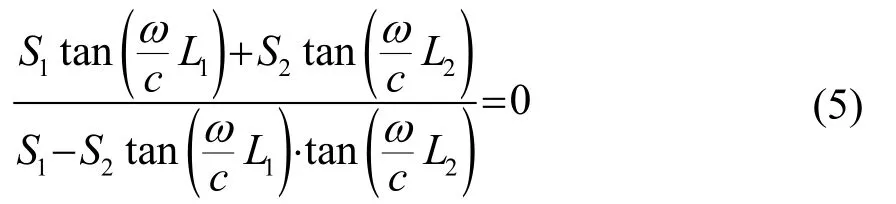
1.2 锥形孔变幅杆

中心孔为锥形的变幅杆的位移函数可表达为

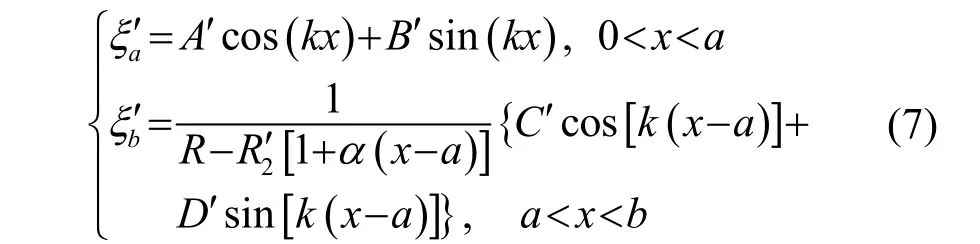
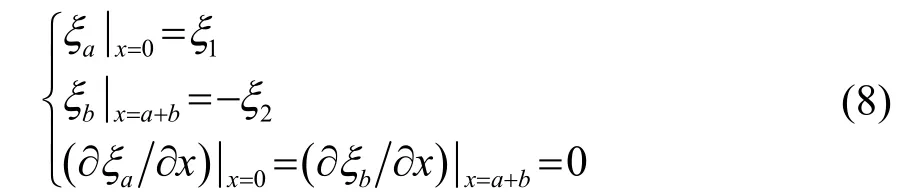
实空两部分连接处的连续性条件为

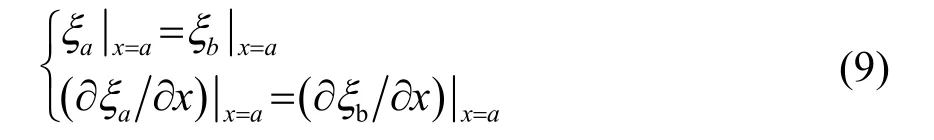
由式(8)、(9)确定常数A、B、C 和D，代入式(7)，得到位移表达式：

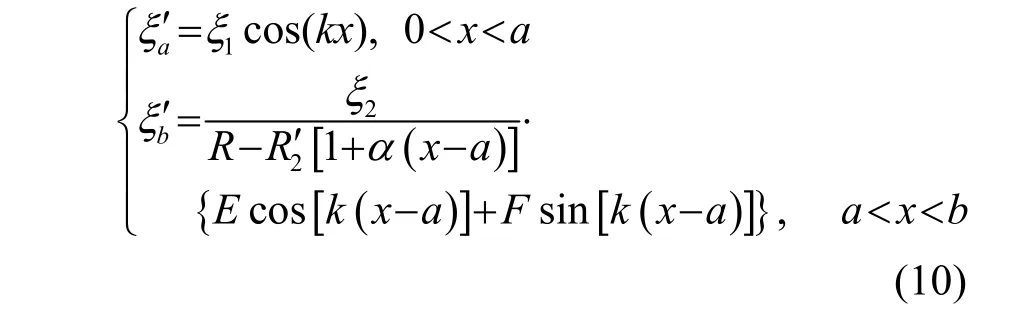
频率方程和放大系数分别为

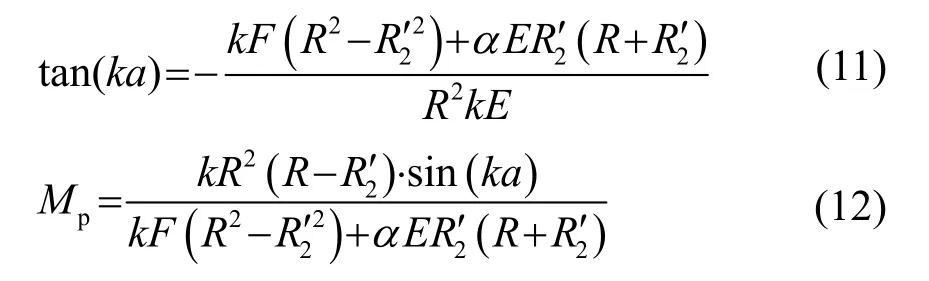
其中：

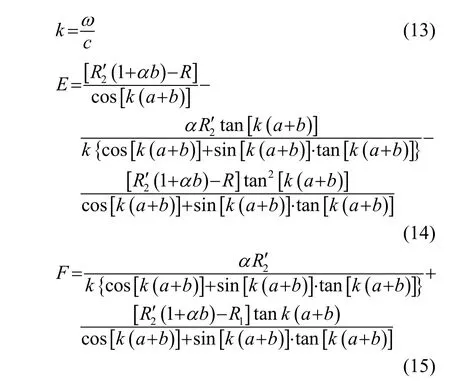
2 性能参数计算

2.1 柱形孔变幅杆

2.1.1 实心部分长度对性能参数的影响

取变幅杆工作频率为20 kHz 时，改变圆柱孔变幅杆实心部分长度的大小，得出1#变幅杆的谐振长度、位移节点和放大系数随实心杆长度的变化规律，如图2 所示。

从图2 中可看出，谐振长度和位移节点位置随L1变化的规律大致相似。当L1的范围为0～30 mm时，谐振长度和位移节点位置随L1的增大而减小；当L1的范围为30～110 mm 时，谐振长度和位移节点位置随L1的增大而增大；当L1大于110 mm 时，谐振长度和位移节点位置逐渐减小。放大系数随L1的增大先增大再减小，当L1=65 mm 时，谐振长度为1L 的两倍，放大系数达到最大。

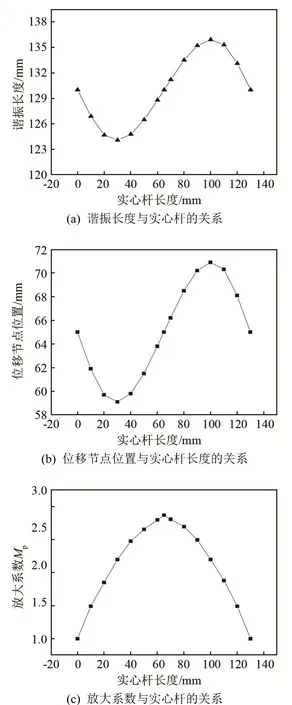
图2 谐振长度、位移节点位置、放大系数和实心杆长度的关系Fig.2 The relationships between resonant length, displacement node, amplification factor and the length of the solid part

2.1.2 中心孔半径对性能参数的影响

保持L1= L2=65 mm、R=26 mm 不变，改变圆柱孔半径大小，计算得出放大系数、谐振频率与中心孔半径之间的关系如图3 所示。

2.2 锥形孔变幅杆小端半径对性能参数的影响

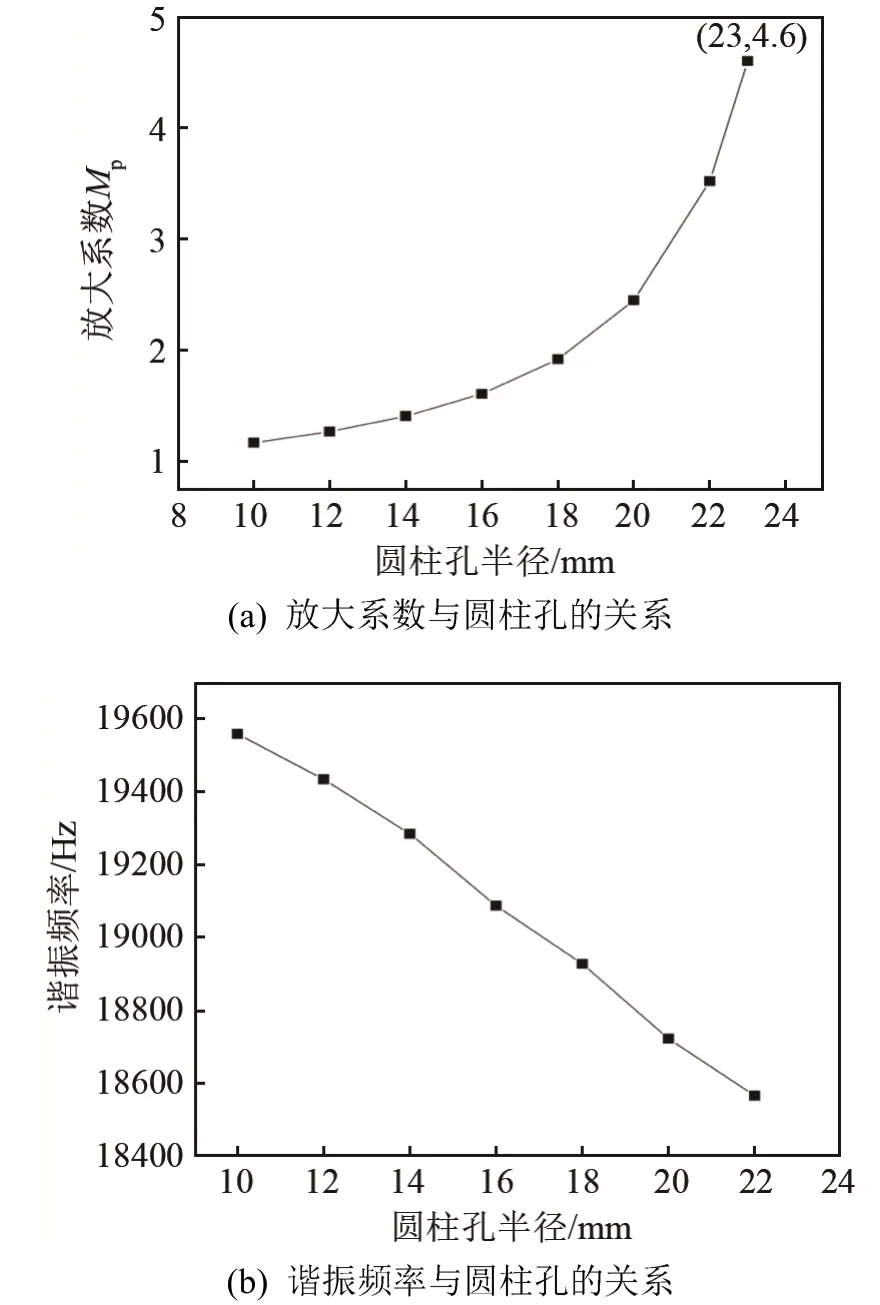
图3 放大系数、谐振频率与圆柱孔半径的关系Fig.3 The relationships between amplification factor, resonant frequency and the radius of the cylindrical hole

由图4 和图5 可知，保持锥形孔变幅杆的外径等其它因素不变，只改变锥形孔小端半径的大小。在谐振状态下，放大系数与应力相对值皆随锥形孔小端半径的增大而增大。

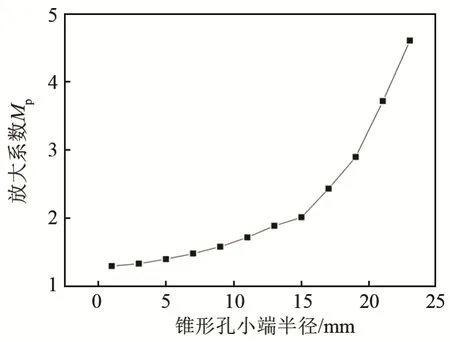
图4 放大系数与锥形孔小端半径的关系Fig.4 The relationship between amplification factor and the radius of the small end of the tapered hole

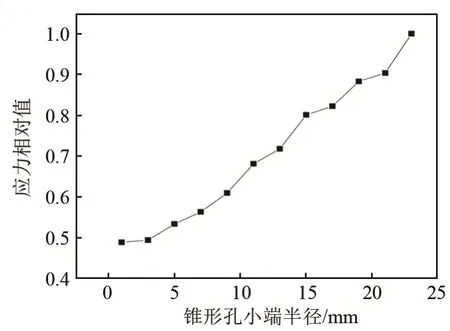
图5 应力相对值与锥形孔小端半径的关系Fig.5 The relationship between the relative value of stress and the radius of the small end of the tapered hole

2.3 两种变幅杆的谐振频率与放大系数的关系

取变幅杆的工作频率为14～25 kHz，圆柱孔变幅杆的圆柱孔半径R1为最大值23 mm，令编号为3#；锥形孔变幅杆的锥形孔小端半径为为18 mm，锥形孔大端半径为 3R′为23 mm，令其编号为4#。代入以上各表达式中，可计算得到两种变幅杆的放大系数与谐振频率的关系，如图6 所示。

由图6 可知，两种孔型变幅杆的放大系数都大于相同外形几何尺寸实心均匀杆的放大系数(实心均匀杆的放大系数为1)。面积系数相同的两种变幅杆在同一频率工作时，柱形孔变幅杆的放大系数比锥形孔变幅杆的放大系数大。

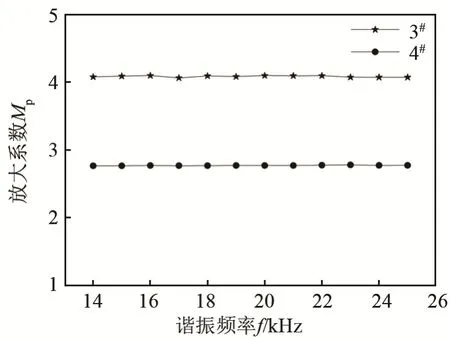
图6 3#、4#变幅杆的放大系数与谐振频率的关系Fig.6 The relationship between amplification factor and resonant frequency of horns 3# and 4#

3 有限元模拟

利用有限元软件建立与3#、4#变幅杆相对应的模型，并进行模态分析，计算了中心孔分别为柱形和锥形、外形为圆柱形的变幅杆在纵振动模态下沿轴向方向的位移和应力分布曲线。将变幅杆输入端振动位移作为位移分布相对值的参考点，在谐振状态下，两种孔型变幅杆沿轴向的位移分布曲线如图7 所示。选择变幅杆实心棒部分任意一点(本文选取32 mm 处)的应力值做参考点进行归一化处理，得到两种孔型变幅杆沿轴向的应力分布曲线，如图8 所示。

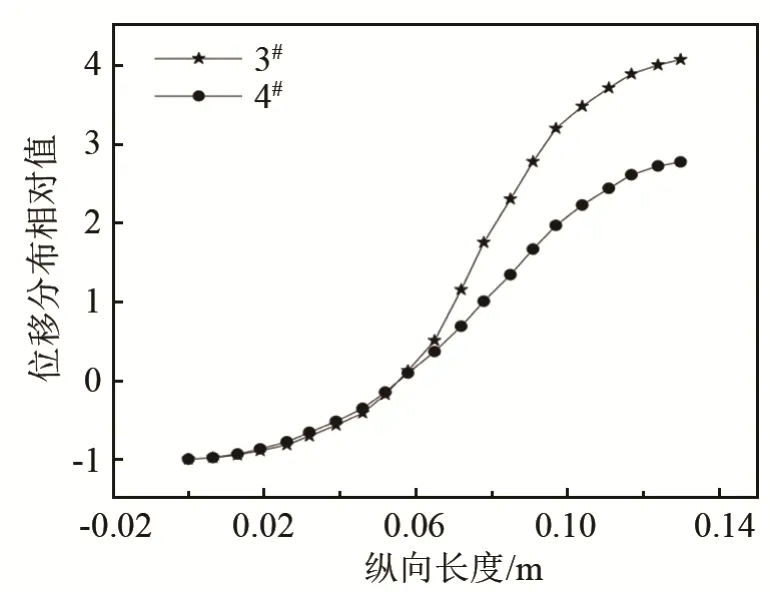
图7 3#、4#变幅杆沿轴向的位移分布Fig.7 The displacement distributions along the axial direction of horns 3# and 4#

从图7 和图8 中可以看出，在相同面积系数与谐振频率下，锥形孔变幅杆的放大系数较小，但归一化后的应力曲线较光滑，且应力最大值比圆柱孔变幅杆的应力最大值降低了57.2%。有限元模拟结果与计算结果较吻合。

4 分析与讨论

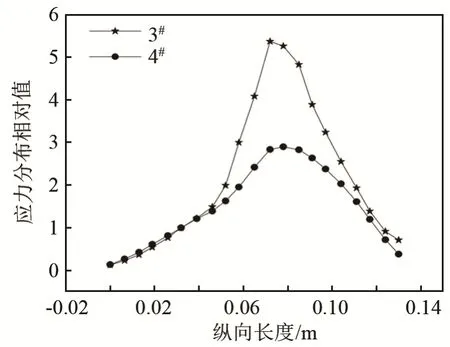
图8 3#、4#变幅杆沿轴向的应力分布Fig.8 The stress distribution along the axial direction of horns 3# and 4#

由图2 与图3 中的数据可以看出，在圆柱孔变幅杆内孔不变的情况下，实心杆长度等于谐振长度的1/2 时，位移节点位于变幅杆的中心位置，且放大系数达到最大；当圆柱孔深度与实心杆长度相等时，放大系数随圆柱孔半径的增大而增大，且变幅杆的输入输出端横截面比率不能超过4.6。

由图4 和图5 可知，保持锥形孔变幅杆的外径等其它因素不变，只改变锥形孔小端半径的大小。在谐振状态下，放大系数与应力相对值皆随锥形孔小端半径的增大而增大。取锥形孔大端半径与圆柱孔所能达到的最大半径(即23 mm)相同时，由图6可知，当两种孔型变幅杆的面积系数相同时，锥形孔变幅杆的放大系数比带圆柱孔变幅杆的放大系数小。当锥形孔变幅杆的锥孔大端突破文献[6]结果的限制，当其小端半径增大至接近23mm 时，纵向振动很难由实心部分传到中孔部分。

图7 和图8 为有限元模拟的结果，两种孔型变幅杆的放大系数都大于实心杆的放大系数(即1)；在相同面积系数与谐振频率下，锥形孔变幅杆的放大系数较小，但归一化后的应力曲线较光滑，且应力最大值比圆柱孔变幅杆的应力最大值降低了57.2%。这很好地验证了上述规律。在实际应用中，可根据对放大系数与应力的不同要求进行选择。