深浅仓卸料压力离散元数值模拟研究

原 方，刘海林，程远浩，杜 乾

1.河南工业大学 土木建筑学院，河南 郑州 450001 2.三明学院 建筑工程学院，工程材料与结构加固福建省高等学校重点实验室，福建 三明 365004

粮食储备库中筒仓储粮占绝大多数，不仅如此，在煤炭、冶金、电力、建材等行业，越来越多的筒仓也被兴建，因此，筒仓安全的重要性不言而喻。

筒仓卸料压力增大机理复杂多变，一直困扰着国内外学者。许多国家的筒仓规范中计算动态侧压力的方法几乎全部采用静压力乘以一个侧压力的修正系数[1-2]，具体方法为：关于深仓动压力，筒仓设计者大多采用Janssen理论，但设计使用的修正系数不同；关于浅仓动压力，多采用Rankine理论和修正后的Coulomb理论。侧压力修正系数过大会造成工程材料的浪费，过小又会威胁筒仓结构安全，因此用合适的侧压力修正系数来准确预测动压力亟须被解决。针对这一难题，刘定华等[3]提出了由整体流动引起筒仓侧壁动压力的计算方法；原方等[4]提出了考虑仓径比影响的一种新的浅圆仓散料侧压力的计算方法，已被筒仓规范采用，主要来解决大型浅圆仓侧压力的计算;孙珊珊等[5]提出了一个基于统一强度理论，考虑3个主应力的共同影响，深仓和浅仓都适用的统一侧压力系数。此外关于超压系数(卸料时的动压力与储料时的静压力之比)，研究发现，卸料过程中动压力达到静压力的2～3倍[6-7]，这是流态的变化或动力拱的形成引起的[8-12]。但截止到目前，尚未出现被广泛接受的合理的理论来准确计算筒仓侧壁上的动压力，仍未搞清动压力的增大机理，无法定性定量的解决这一科学问题。

作者在试验验证的基础上，运用离散元软件PFC2D建立6个高径比(H/D)不同的模型筒仓进行数值模拟，其中3个深仓(H/D>1.5)高径比分别为2.9(模型仓a)、2.2(模型仓b)和1.76(模型仓c),3个浅仓(H/D<1.5)高径比分别为1.47(模型仓d)、1.28(模型仓e)和1.1(模型仓f)，对静压力、动压力以及超压系数进行对比分析，另外从流态和动力拱两个不同的角度来分析筒仓侧壁动压力增大的情况，为能准确预测筒仓侧壁动压力的计算公式提供推导依据，为构建筒仓结构安全设计的机理研究提供参考。

1 模型仓试验和数值模拟

1.1 试验模型仓

试验采用有机玻璃筒仓，便于观察卸料过程中小麦的流态，底部漏斗高0.7 m，筒仓仓壁高5.5 m，装料高4.4 m。配套设备有中转仓、斗提机和传送带，可以实现玻璃筒仓入料和卸料的机械化，如图1所示。试验所用小麦重力密度为8 kN/m3，内摩擦角为25°，外摩擦系数为0.4，小麦物理参数选取参考文献[8]。

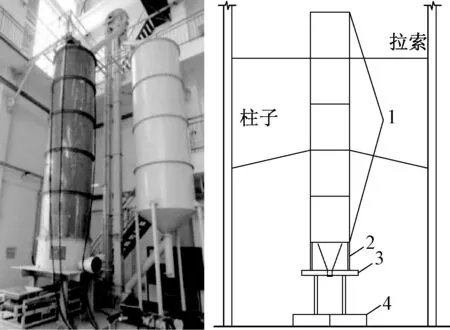
1. 筒仓筒体; 2. 带孔漏斗; 3. 钢制筒台; 4. 平台钢架图1 模型筒仓及结构图Fig.1 Model silo and structure

试验采用中心卸料方式，传感器布置如图2所示。A、B、C每列分别布置10个土压力传感器，D列布置4个薄膜传感器。

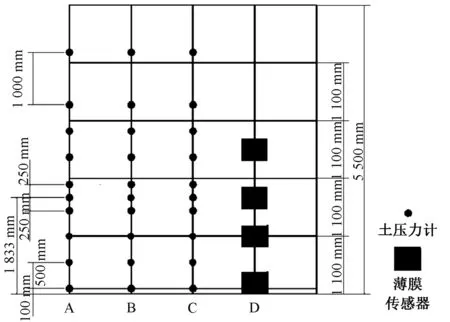
图2 仓壁传感器立面图Fig.2 Sensor elevation layout of silo wall

1.2 模拟模型仓

模拟模型仓以试验筒仓为原型，装料高度4.4 m，模型调试采用控制变量法，通过对模型试验数据进行反复标定以确定模型的各项物理参数[13]，模拟模型仓的各项主要材料参数为：墙体法向刚度1.0×107Pa，墙体切向刚度0.5×107Pa，颗粒法向刚度1.0×106Pa，颗粒切向刚度0.5×106Pa，颗粒重力密度800 kg/m3，颗粒外摩擦系数0.4，颗粒内摩擦系数0.5，模型仓a测点深度及满仓状态如图3所示。

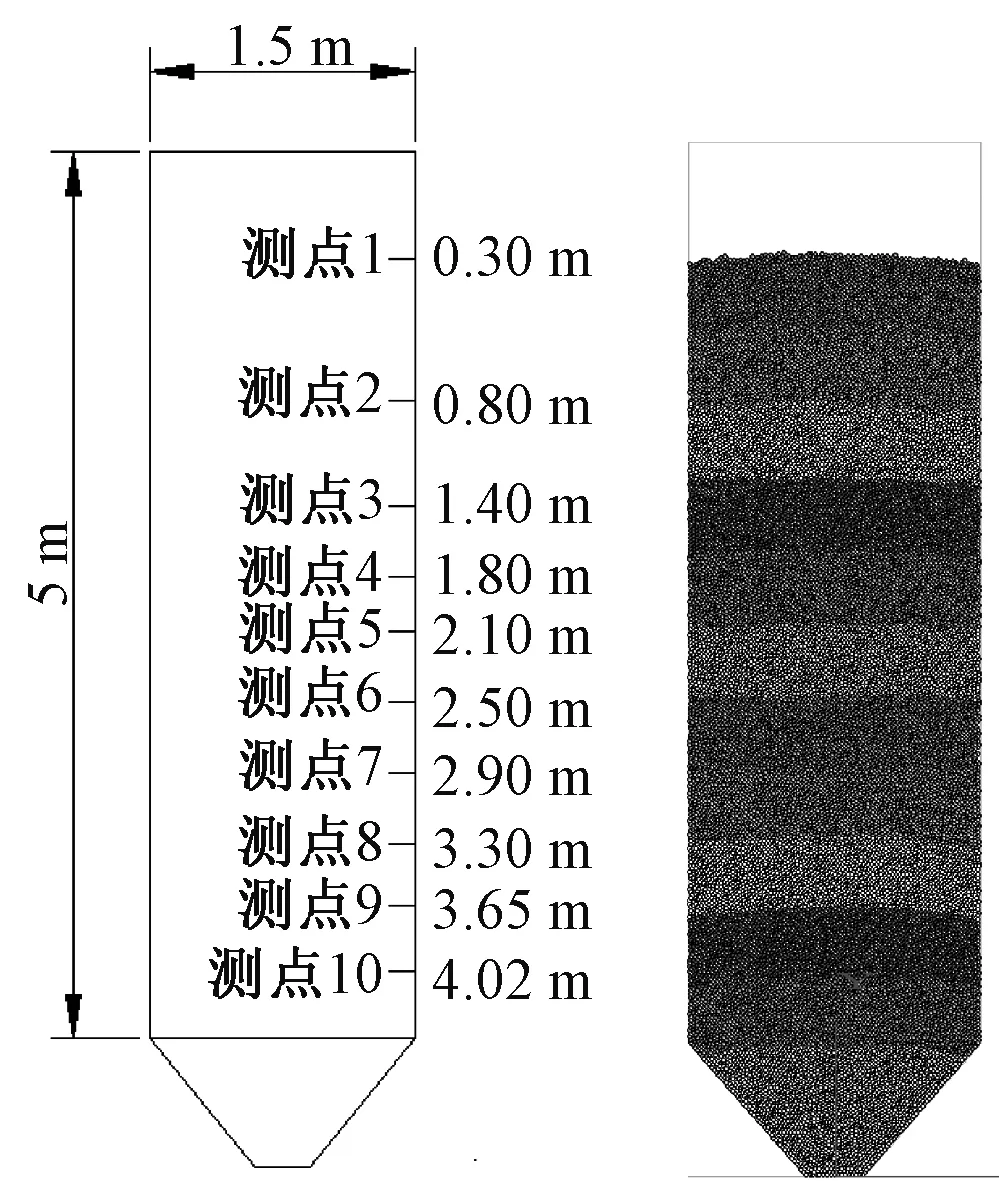
图3 模型仓a测点深度及满仓状态Fig.3 Depth and full filling state of tested point ain a model silo

1.3 试验结果与模型仓a模拟结果对比分析

图4中试验静压力和动压力是A、B和C 列中传感器所得平均值，由图4可知，模拟的静压力与试验的静压力总体趋势一致。试验最大动压力发生在筒仓下部大约1/3处，为12.23 kPa，模拟最大动压力发生在筒仓下部大约1/4处，为18.26 kPa。试验超压系数是A、B和C 列中传感器平均动压力与平均静压力的比值,结果如图5所示，试验最大超压系数发生在筒仓中下部位置，为2.05，模拟最大超压系数发生在筒仓下部位置，为2.48。由图4和图5可知，试验结果与模拟结果不尽相同，一方面是由于计算机技术的限制，小麦粒径设置过小则无法进行计算，数值模拟时所采用的粒径为8 mm，与试验仓所使用的小麦粒径不同；另一方面是由于模拟模型仓侧壁与漏斗相交处附近，边界条件设置复杂，文中为简化模型，此处设置为线性接触，但误差在可接受的范围内。

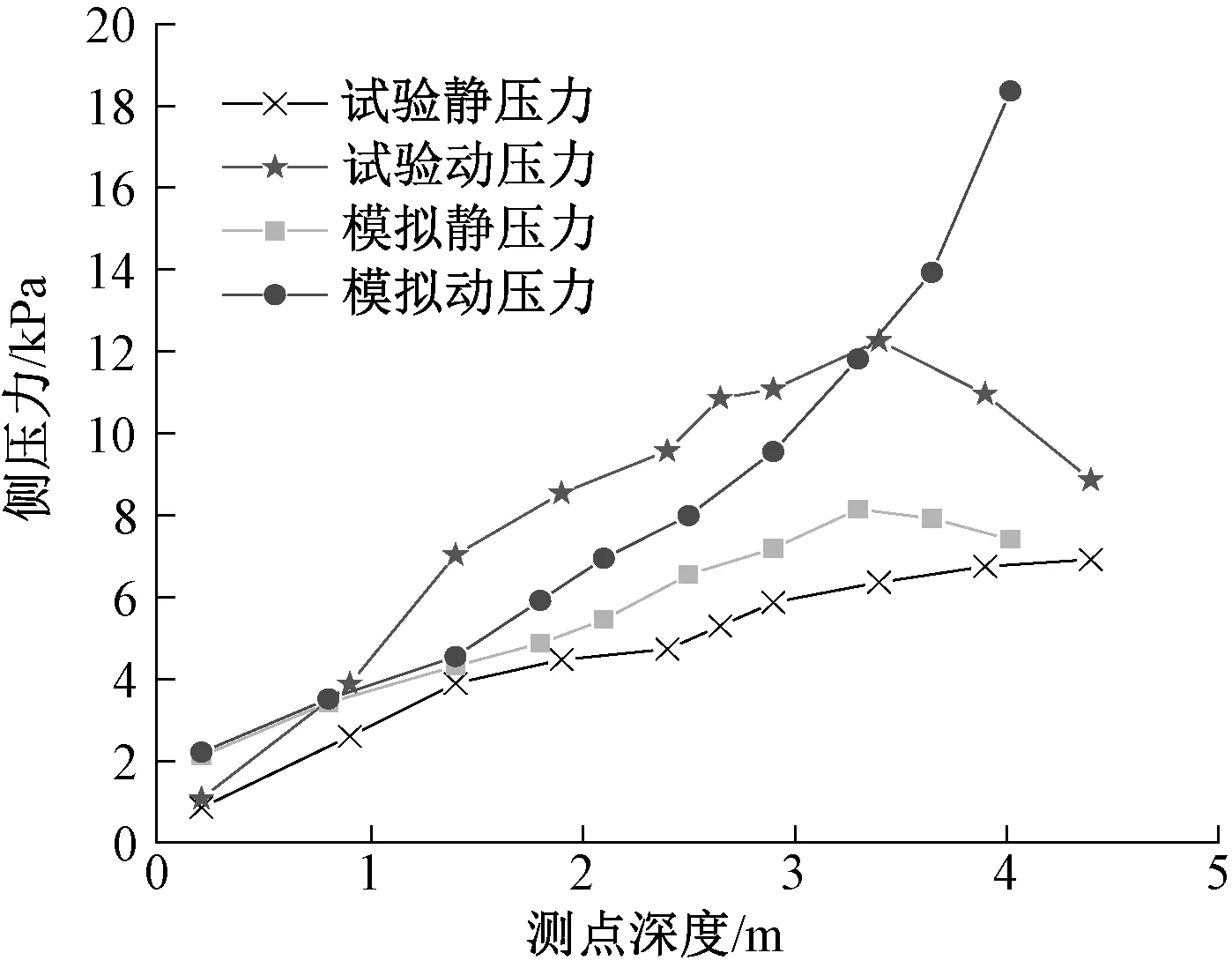
图4 试验与模拟的静压力、动压力对比Fig.4 Comparison of static pressure and dynamic pressure between experiment and simulation

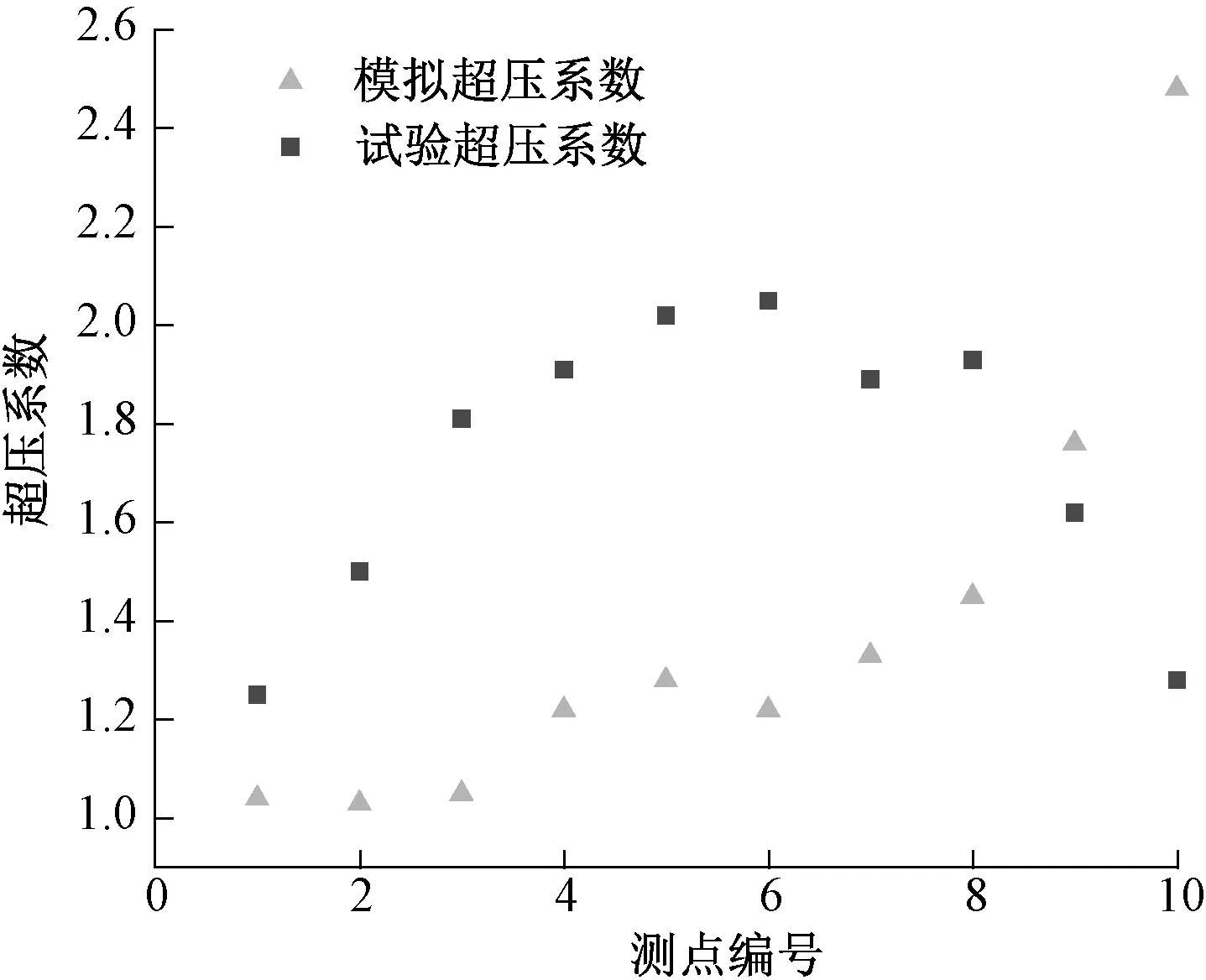
图5 试验超压系数与模拟超压系数对比Fig.5 Comparison of experimental overpressure coefficient and simulated overpressure coefficient

2 高径比不同的深浅仓数值模拟

2.1 高径比不同的深浅仓模拟模型

所有的模拟模型仓装料高度、测点布置深度以及建模时所用的材料属性参数相同，不同的只是筒仓直径以及卸料口宽度。卸料口宽度为筒仓直径的1/5，底部漏斗倾角50°，模型筒仓装粮高度4.4 m，模型仓a仓径1.5 m，模型仓b仓径2 m，模型仓c仓径2.5 m，模型仓d仓径3 m，模型仓e仓径3.5 m，模型仓f仓径4 m。

2.2 高径比不同的深浅仓模拟结果分析

从PFC2D软件中提取模型仓b卸料压力曲线如图6所示，横坐标表示筒仓卸料时步(时步为PFC2D软件中进行迭代得到最终状态的计算单位)，前期曲线的平线段表示各个不同深度测点的静压力，由图6可知，最大卸料压力发生在卸料初期，大约在2.5×105时步处，发生超压且现象明显，且在卸料过程中，同一高度的卸料压力并不是一直增大或减小，而是出现上下震荡。其他模型仓与之类同。

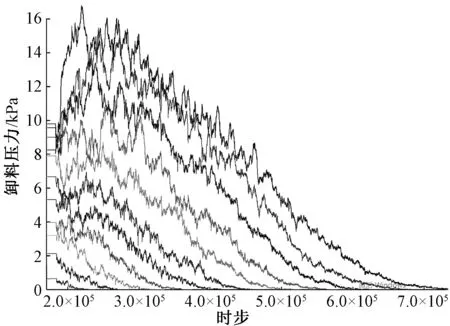
图6 PFC中模型仓b卸料压力曲线Fig.6 Discharge pressure curve of model b in PFC

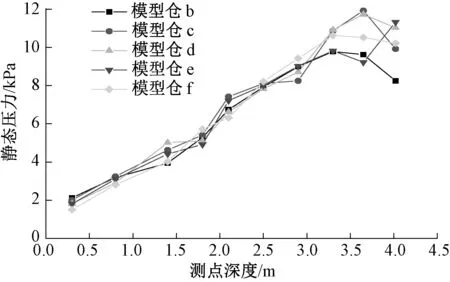
图7 高径比不同的5个模型仓静态压力值对比Fig.7 Comparison of static pressure values of five model silos with different height diameter ratios

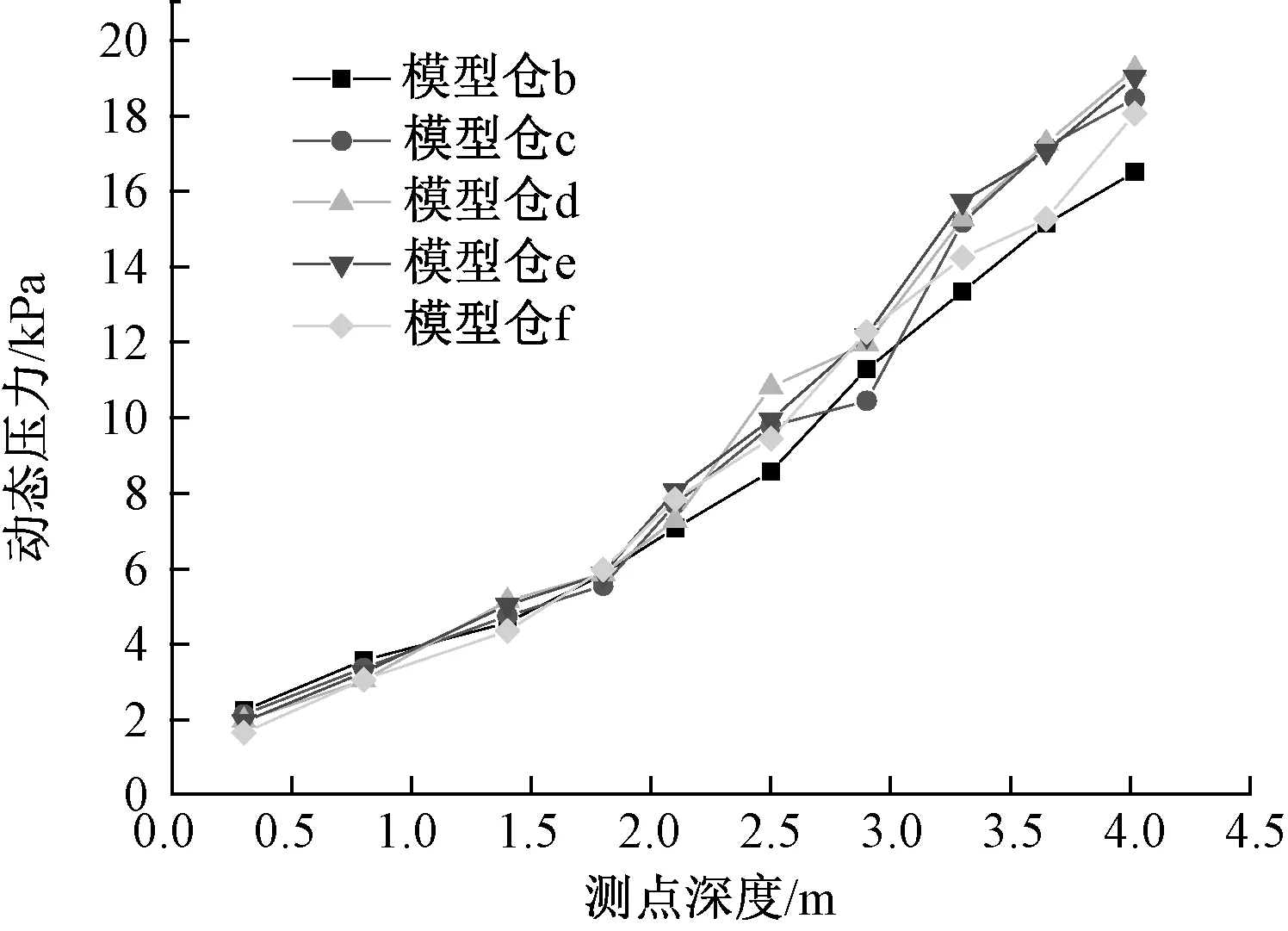
图8 高径比不同的5个模型仓动态压力值对比Fig.8 Comparison of dynamic pressure values of five model silos with different height diameter ratios

图9 高径比不同的5个模型仓超压系数对比Fig.9 Comparison of overpressure coefficient of five model silos with different height-diameter ratios

高径比不同的5个模型仓静压力对比、动压力对比、超压系数对比如图7—图9所示，可以发现：(1)动压力明显大于静压力，筒仓下部位置最为明显。(2)深仓模型与浅仓模型动压力相差不大，模型仓b最大动压力16.42 kPa，模型仓c最大动压力18.43 kPa，模型仓d最大动压力19.21 kPa，模型仓e最大动压力19.01 kPa，模型仓f最大动压力18.03 kPa，由前文知模型仓a的最大动压力18.36 kPa，且最大动压力均发生在筒仓下部位置。可以看出，相同高度、较大直径的筒仓最大动压力随直径增大呈整体上升趋势，但非线性，这与付建宝[14]发现的一致，同时也说明了设计浅仓时，只采用Rankine理论和修正后的Coulomb理论作为设计值，不考虑动态压力的修正是不科学的。

3 动态压力增大原因分析

3.1 从贮料流态的角度分析

颗粒在离散元软件PFC2D中分层生成，结果如图10所示。由于模拟数据较多，故下文中卸料过程、速度场和力链场，深仓以模型仓a为例，浅仓以模型仓f为例。

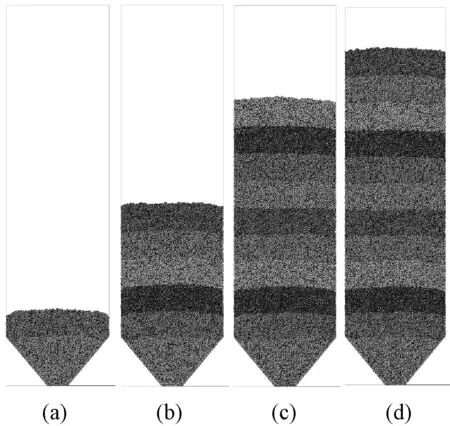
注：(a)、(b)、(c)、(d)表示时步分别为2.3×105、3.3×105、5.3×105、6.3×105，图11—图16同。图10 筒仓内散体颗粒生成过程Fig.10 Formation process of bulk particles in silos

筒仓内贮料在重力作用下流动，可分为整体流动和管状流动，整体流动为筒仓内贮料均匀向下运动，同一高度的贮料保持在同一水平上；由于筒仓下部截面形态的变化阻碍了筒壁处贮料的运动，导致筒壁处的贮料流动缓慢或存在短暂的死料区，使得筒仓下部处于同一水平面上的贮料出现逐渐增大的速度梯度，从而形成管状流动。如图11所示，模型仓a卸料前中期，筒仓内贮料呈整体下落态势，即每层颗粒基本上保持矩形形状不破坏，在重力作用下整体下落；筒仓内贮料大概剩余初始1/3时，开始出现管状流动，中间颗粒流动速度明显大于两侧，上表面开始凹陷，卸料逐渐从单一的整体流动变为整体流动与管状流动混合的卸料方式，且与试验观察到的流态高度一致。如图12所示，模型仓f卸料前期，筒仓内颗粒整体流动，筒仓内贮料大概剩余初始2/3时，开始出现管状流动，与深仓模型a一致，开始出现混合流，并且可以发现，当筒径足够大时，整体流动状态不再出现。整体流动是筒仓设计首选流态，具有料流稳定、不结块以及不分离的优点，通过改流装置使管状流动转变为整体流动，且发现筒仓侧壁压力峰值减小[15]，故前文所述浅仓相对于深仓卸料压力峰值偶有增大，两者流态的不同是卸料压力不同的重要原因之一。但Mathews等[16]也指出很难在整个卸料过程实现“先进先出”的整体流，因仓壁与贮料的剪切力极易造成贮料流动的速度梯度，从而在卸料末期形成漏斗流。

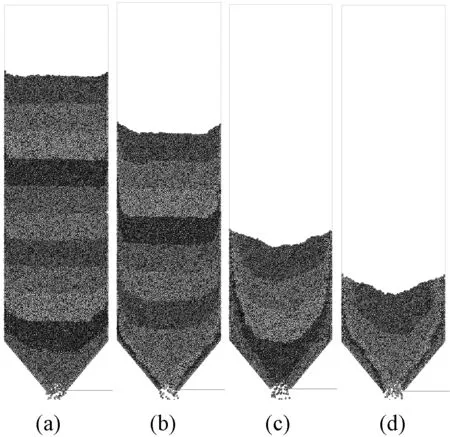
图11 深仓模型a卸料过程Fig.11 Discharging process of deep silo model a

图12 浅仓模型f卸料过程Fig.12 Discharging process of shallow silo model f

如图13和图14所示，无论模型仓a还是模型仓f，随着卸料时间的延长，筒仓中间的颗粒流动速度要比两侧颗粒流动速度快，导致模型仓a卸料后期，模型仓f中后期上层贮料最先流出，这与上文所讨论的流态相一致。

图13 深仓模型a卸料速度场Fig.13 Discharging velocity field of deep silo model a

图14 浅仓模型f卸料速度场Fig.14 Discharging velocity field of shallow silo model f

3.2 从贮料结拱的角度分析

筒仓内贮料在仓壁截面变化处形成挤压流动，使贮料在该处不断形成结拱-塌拱的状态，即不断形成动力拱，从图15和图16可以看出，无论是深仓还是浅仓，筒仓侧壁附近的力链随着筒仓深度的加深而变得密集，即接触力越来越大，并且在卸料过程中，筒仓中心的贮料流动速度快但接触力小，贮料迅速减少形成的动力拱则会抑制两侧的贮料，两侧的贮料流动速度慢但接触力大，这种速度的不同造成了力学梯度，使筒仓内的贮料在流动时受到剪切混合力的作用，分布形态成非水平状态即力链在水平方向上分布的不均匀, 是造成压力凹陷[17]的主要原因。与王学文[9]发现的情况一致，并且结拱所需时间与筒仓尺寸有关，对于圆筒仓而言，直径越大贮料颗粒在卸料过程中结拱所需时间也就越长，贮料颗粒本身还未来得及调整结拱的最佳位置却已经下移，那么结拱的可能性就越小,这是卸料时浅仓相对于深仓卸料压力不同的重要原因之一。

图15 深仓模型a卸料力链场Fig.15 Discharging force chain field of deep silo model a

图16 浅仓模型f卸料力链场Fig.16 Discharging of focus chain fieldshallow silo model f

4 结论

从筒仓高径比入手，采用室内模型试验法和离散单元法研究贮料在静态储粮状态和卸料过程中的力学行为。试验最大动压力发生在筒仓下部约1/3处，为12.23 kPa，模拟最大动压力发生在筒仓下部约1/4处，为18.36 kPa；试验最大超压系数发生在筒仓中下部，为2.05，模拟最大超压系数发生在筒仓下部，为2.48。经过对高径比不同的6个深浅仓模型的结果分析，相同高度、较大直径的筒仓最大动压力随直径增大呈整体上升趋势，但非线性。在卸料过程中，筒仓最大卸料压力发生在卸料初期，同一高度的卸料压力并不是一直增大或减小，而是在卸料压力的增大或减少的趋势下出现上下震荡。深仓模型a内贮料大概剩余初始1/3时，浅仓模型f内贮料大概剩余2/3时，开始出现管状流动，中间颗粒流动速度明显大于两侧，上表面开始凹陷，卸料逐渐从单一的整体流动演变为整体流动与管状流动混合的卸料方式，两者流态的不同是卸料压力不同的重要原因之一。无论是深仓还是浅仓，筒仓侧壁附近的力链随着筒仓深度的加深而变得密集，即接触力越来越大，并且在卸料过程中，筒仓中心的贮料流动速度快但接触力小，贮料迅速减少形成的动力拱则会抑制两侧的贮料，两侧的贮料流动速度慢但接触力大，并且结拱所需时间与筒仓尺寸有关，对于圆筒仓而言，直径越大贮料颗粒在卸料过程中结拱所需时间也就越长，贮料颗粒本身还未来得及调整结拱的最佳位置却已经下移，那么结拱的可能性就越小,这是卸料时浅仓相对于深仓卸料压力不同的重要原因之一。