基于二次卡尔曼滤波修正的尾气排放分布

林建新， 云 旭， 李京冕， 商鹏飞

(1.北京建筑大学北京市城市交通基础设施建设工程技术研究中心， 北京 100044；2.北京建筑大学首都世界城市顺畅交通协同创新中心， 北京 100044)

随着城市快速发展、机动车保有量逐年增加，交通拥堵导致的尾气排放问题日益严重. 数据表明，尾气排放占大气污染的20%～30%，其中包括一氧化碳、碳氢化合物、氮氧化合物和颗粒物[1]. 目前建立尾气量化模型是辅助决策者制定策略的主要方法，主要分为宏观、中观、微观3个层次[2]，相对于发达国家，中国尾气排放模型体系尚不完善，燃料燃烧、发动机运行状态等因素导致机动车尾气排放差异显著. 近年来国内对尾气排放与环境因素关系、机动车工况条件对于尾气排放敏感性及交通量对于尾气排放影响相关研究不断涌现，而基于机动车比功率(vehicle specific power，VSP)的排放测算方法由于与污染物排放具有较好一致性，且获得、计算相对便捷及物理可解释性等特点[3]，广泛被学者研究使用. Song等[4]通过分析逐秒速度数据和油耗，提出VSP分布可用于计算单位时间的油耗，但未实现对连续交通网络数据采集. 李笑语等[5]利用基于射频识别技术(radio frequency identification，RFID)和视频识别数据获取南京市450个主次干路基站实时动态交通数据，朱倩茹等[6]运用GPS浮动车数据分析广州市机动车排放量分布特征，方法上由于逐秒数据精准采集受限，网络尾气排放量化受到制约. 宋国华等[7]发现不同平均速度下，VSP分布正态分布特性，结合污染物排放提出不同速度区间下的形式周期修正因子[8]. 虽然VSP与平均速度的关系体系相对完善，但通过模型标定高质量的交通需求数据，进而得到平均速度，结合工况进行机动车尾气排放分析还有进一步深入研究的价值和意义.

1 问题分析

总的来看，建立宏观尾气模型是解决尾气排放问题的一种途径，但模型建立的关键点在于获取与排放因子相匹配并能反映道路实际行驶特征的交通活动数据. 利用集计分析方法得到区域内的尾气排放分布情况时，由于数据的时空分辨率不高，无法得到路网中各个路段不同时间的尾气污染及分布情况，精确获取VSP中全路网平均速度也相对困难. Cook等[9]基于交通需求模型(travel demand model，TDM)获取逐时的路段流量，姚志良等[10]选取了北京市的典型路段，记录了逐秒的车辆位置和速度，Iqbal等[11]选择代表性的道路调查机动车行驶里程和交通量数据. 但是，通过调研或人工采集法只可获取静态数据，其覆盖道路少，准确度低，数据量不大，导致计算排放的结果会产生较大误差. 同时静态数据不具备周期更新特点，其数据有效性及滞后性仍存在较大问题.

路网化的尾气排放分布问题属于宏观范畴，其量化不仅与交通流宏观特性有关，还与车辆的行驶工况密切相关. 按照“交通需求推演—VSP参数确定—交通排放”的思路，解析交通需求与尾气排放的机理和关键因素，利用二次卡尔曼滤波法改进交通流量需求预测方法，提高断面交通流量数据和动态起讫点(origin destination，OD)精度，再通过交通需求推演的方法获取路段平均速度，建立平均速度与VSP的关系模型，获取代表车型的时间- 速度曲线量化分析区域内尾气排放分布，实现对各路段、不同时段的交通排放监控.

2 基于卡尔曼滤波的交通流量预测模型改进

在动态交通预测理论中卡尔曼滤波法应用较广泛. 卡尔曼滤波器用反馈控制的方法估计过程状态[12]，其过程可分为2个部分：时间更新方程和测量更新方程. 时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值，为下一个时间状态构造先验估计；测量更新方程负责反馈，利用预估过程的先验估计反馈当前状态的后验估计，并根据这种预估- 校正算法对时间、状态进行同步更新，并根据反馈结果自行校准误差[13-14].

由于卡尔曼滤波具有线性无偏最小均方差性等特点，故在短时交通预测中应用广泛. 但在交通流数据采集实践中发现，拥挤网络中应用卡尔曼滤波进行短时预测会产生较大的误差[15]. 因此，本文将改进模型获得全状态下准确的短时交通流预测结果，为实现以交通需求为手段的尾气排放强度化分析提供支撑.

2.1 基于卡尔曼滤波理论的传统预测模型

设QL(f+k)表示路段L上f时刻以后k个时间段的车流量，Qin(f)表示流入交通量，Qout(f)表示流出交通量，在交通系统中考虑交通流的连续性，根据流体守恒定律可得

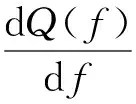
(1)

即

Q(f)=Q(f-1)+[Qin(f)×Qout(f)]Δf

(2)

假设流入流出交通量受前3个时刻交通量的影响，即

Qin(f)=C11Qin(f-1)+C12Qin(f-2)+C13Qin(f-3)

(3)

Qout(f)=C21Qout(f-1)+C22Qout(f-2)+
C23Qout(f-3)

(4)

式中C为各历史时刻的流入流出量对现交通量的影响因子. 将式(3)(4)分别带入式(2)中，得

Q(f)=H0v(f-1)+H1v(f-2)+H2v(f-3)

(5)

式中：H0=[C11-C12]Δf、H1=[C21-C22]Δf、H2=[C31-C33]Δf为时变参数组成得时变向量；v(k)=[Qin(f)Qout(f)]T为流入流出交通量组成的向量.

由此得到考虑历史数据的交通量预测模型应为

Q*(f+1)=H0v(f)+H1v(f-1)+H2v(f-2)+ω(f)

(6)

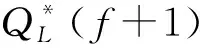
考虑该预测模型为时间序列的回归模型. 待定参数Hi可用状态空间的形式将其表示，由此应用卡尔曼滤波理论进行状态变量的估计及计算，将交通流理论中各参数进行了变换

A(f)=[vT(f),vT(f-1),vT(f-2)]

(7)

X(f)=(H0,H1,H2)T

(8)

(9)

由此可得

X(f)=B(f)X(f-1)+u(f-1)

(10)

Z(f)=A(f)X(f)+w(f)

(11)

利用卡尔曼滤波理论得到方程组

(12)

P(f|f-1)=B(f-1)P(f-1)BT(f-1)+V(f-1)

(13)

K(f)=P(f|f-1)AT(f)[A(f)P(f|f-1)AT(f)+
R(f)]-1

(14)

(15)

P(f)=[I-K(f)A(f)]P(f|f-1)

(16)

应用卡尔曼滤波模型对交通流进行预测时预测步骤.

步骤1设定初始参数

设定模型初始参数值，如图1所示，将状态转移矩阵初始值B(1)设为M维单位矩阵；过程噪声相关矩阵V(f)设置为M维的随机噪声矩阵，在MATLAB中定义为cov(randn(m,m))；由于预测的是一维时间序列，故将R(f)设置为一维随机数，在MATLAB中定义为randn(1,1)； 在实际测量过程中很难确定系统状态向量的初始值X0，但由于卡尔曼滤波在迭代中不断对估计值进行预测并修正，因此预测模型会逐渐趋于稳定，初值的选取对系统最终结果影响也会衰减. 故可将系统状态向量初值与观测向量初值设置相等，将初始协方差矩阵P0设置为零矩阵.

设置状态转移矩阵B(f)：状态转移矩阵在平稳时间序列模型的情况下，如果知道其值便可根据状态空间方程描述非平稳情况，但在交通系统中无法获取状态矩阵，且交通系统可以认为是一个慢变系统，因此可将状态转移矩阵B(f)设置为单位阵.

步骤2卡尔曼滤波法递推预测

选取一条道路作为实验对象，以15 min为周期. 卡尔曼滤波预测值与观测的真实值的比较如图2所示.

卡尔曼滤波相对误差如图3所示.

由图2、3结果可知，与真实值对比，在滤波稳定期其相对误差均在10%以内. 预测结果可为后续工作提供高精准度数据.

2.2 OD矩阵修正

动态交通分配，通过采集实时交通数据资料不断更新出行分布. 利用交通分配得到路段实时交通量，由于根据断面流量的部分样本数据反推OD存在误差导致结果不准确，造成了误差的积累，使分配结果准确度降低且错误持续叠加[16]，因此，应用卡尔曼滤波进一步修正，以获取高精度OD矩阵，进行推演预测.

卡尔曼滤波法修正OD矩阵. 为使计算结果更接近真实值，为平滑处理交通流量的原始数据，使用采集的邻近2周同时间段交通流量作为历史数据作为历史规律比对基数，引入最初OD反推矩阵作为初始值，利用相应时段最优历史值的偏差作为状态变量，路段流量作为观测变量.

矩阵形式下的状态转移方程为

(17)

观测方程为

(18)

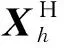
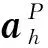
从标定结果可以看出，随车流密度增大，断面观测流量的占比权重也随之增大；历史数据权重占比呈现明显的双峰. 由图4、5可知，阻塞流状态下，交通流密度较大，后车速度受前车制约性强，车辆行驶自由度小，车辆稳定性差，显示出较大的波动性，在拥挤状态下交通流呈现走走停停的状态，对于短时的交通流预测不利，基于原始线性模型的卡尔曼滤波对于此状态适用性不强，故拥挤状态下权重占比会增大.

从计算结果可以看出，在架设雷达检测器的断面上，利用改进卡尔曼滤波修正的OD矩阵进行推演的结果与实际观测交通量比较，计算其平均相对误差为8.89%，最大相对误差为15.2%.

卡尔曼滤波在预测相对稳定的系统时，在经历了滤波初期的训练期之后预测效果很好，其根据每一次计算的误差进行不断校正以此使误差减小. 但由于滤波初期状态向量不准确，即初始状态向量设定为假定值，使初期误差增大，故出现最大相对误差较大的情况. 但平均相对误差满足精度要求[17-20]. 实验结果表明该方法可行，并据此建立精准的交通需求预测模型.

3 交通排放模型

交通需求预测保证了数据的准确性，为尾气排放模型的建立提供了良好的数据来源. 但不同地区的地理状况、环境因素、车辆组成的影响决定了应用尾气排放模型时工况特征参数的地区差异性. 通过调查地区的特征参数及对参数的简化处理，应用更适合处于发展中国家复杂的机车组成结构的IVE尾气排放模型进行量化分析.

3.1 VSP分布率的获取

在交通排放量化过程中，VSP对油耗排放有明确的物理意义和很好的相关性，基于VSP研究的理论方法也逐渐被应用于此类研究中. Jiménez-Palacios[21]提出的利用速度及加速度获得轻型车VSP计算公式

VSP=v(1.1a+0.132)+0.000 302v3

(19)

式中：v为实时速度，m/s；a为实时加速度，m/s2.

由于逐秒的交通流数据困难，宋国华等[7]研究表明：当平均行程速度大于20 km/h时，VSP分布服从正态分布，分布均值为对应平均行程速度值的匀速VSP值，分布的标准差可用平均行程速度的幂函数描述，实例验证表明，研究建立的VSP分布模型可用于道路油耗的测算. 其VSP分布严格服从正态分布，概率密度函数公式为

(20)

式中：μ为均值；σ为标准差.μ与σ均可由平均速度获取，其计算公式为

(21)

σ=0.832s0.396 1

(22)

式中s为平均行程速度，km/h.

基于以上研究方法，便可建立VSP分布模型与平均速度相关性. 将2.2节中交通需求分配得到的路段平均速度代入式(19)中即可计算出该平均速度或平均速度区间下的VSP分布率.

3.2 工况特征参数获取

简易机动车行驶工况法特征参数获取[22]：在考虑城市道路布局、交通组成方式、土地利用形式以及居民出行习惯等多种因素后，确定了市域代表性路段，并以此作为该地区机动车行驶工况的典型路线.

表1 典型机动车行驶路段长度 Table 1 Typical link length of vehicles driving km

针对该典型路段，主要集中在夏、冬2个季节的早、中、晚3个时间段进行筛选(7:00—9:00、11:30—13:00和17:00—19:00)，从总体数据中随机抽取不同的行驶周期组成900～1 000 s的数据段作为备选机动车行驶工况，以平均速度(v1)、平均行驶速度(v2)、平均加/减速度(A/D)、怠速比例(Pi)、加/减速比例(Pa/Pd)、匀速比例(Pc)、相对正加速度、正加速度动能和每100 m速度振荡次数等11个特征参数为行驶特征参数及市域的机动车行驶特征参数.

表2 机动车行驶工况特征参数

计算得到的机动车行驶特征参数，对应各车型的时间速度曲线如图7所示.

3.3 排放模型的选取及应用

根据中国实际情况，选取更适合处于发展中国家复杂的机车组成结构的基于机动车行驶工况的IVE模型.

IVE模型具有排放物种类多、机动车燃料种类多及可计算不停运行状态下的排放量等特点. 其计算方法在本质上与MOBILE模型的方法类似，即利用模型内嵌的基准排放因子乘以一系列修正参数从而得到当地城市每种技术类型机动车的排放因子，基本计算过程[23]为

Qt=BtK1tK2tK3t…Knt

(23)

(24)

(25)

K=Emea/Eive

(26)

式中：Qt为修正后的基准排放因子；Bt为基准排放因子；Q是整个车队的平均排放因子；ft为某技术类型车辆的动态组成百分比；fdt为某技术类型车辆行驶或停机的百分比组成；UFTP为LA4工况的平均速度(常数)；D为车辆行驶距离；UC为特定行驶工况的平均速度；K1tK2tK3t…Knt为一系列修正系数；Kdt为车辆动态组成修正系数；t表示车辆技术类型；K表示修正系数，Emea表示机动车污染物的车载排放测试值单位；Emea表示IVE模型基本排放因子值.

通过对观测点雷达采集的数据使用TransCAD分析，可知该时段某一路段的平均速度，将所得车流的平均速度与上述机动车车型行驶工况进行匹配，引入速度相对误差的概念[24]

(27)

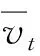
在对每个区域进行问卷调查，得到居民行车习惯修正参数后，计算速度相对误差，将小于或等于10%的数据认为是同一车型机动车，然后将对应的工况参数带入IVE尾气模型计算出此时的尾气排放强度，并将数据导入到MATLAB中得出尾气排放强度云图，如图8所示.

在对某测点进行了抽样调查后，分别得到一氧化碳(CO)及氮氧化物(NOx)模型值与实地测量值对比结果，见表3、4.

由表3、4可以看出，模型排放强度计算值普遍小于排放测试结果，模型预测的CO平均相对误差为14%，NOx平均相对误差为23%，原因是由于实验场景和器材的限制，无法对车队启动次数、尾气排放量等参数精确测量，本实验通过测量测站临近范围内的排放因子平均值作为经过该测站车队排放强度的总和，但测站的周围环境因素(如工厂、住宅、排放因子扩散等)所传播的碳、氮氧化物皆对测定的实验结果产生影响.

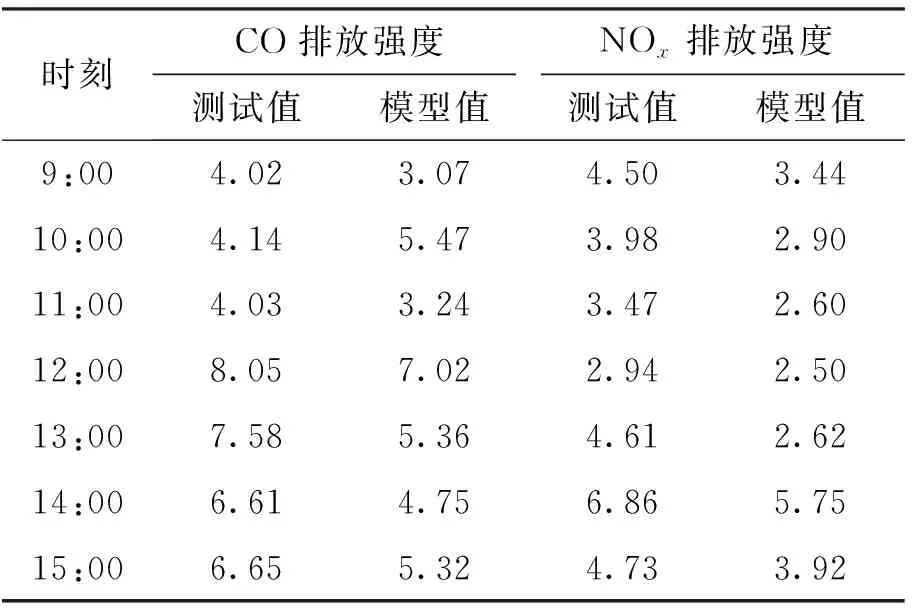
表3 某主干路测点尾气排放强度预测值与观测值对比

表4 某主干路测点尾气排放强度误差分析

以CO排放强度为例，由图9、10两张分布图对比分析得出，随着交通量增加，道路尾气排放强度出现峰值的概率增加，但受到机动车工况、通行车辆类型等多种因素影响，如交通需求量虽大，但道路V/C比不大时，相对拥堵所产生的尾气排放强度较少. 尾气排放强度与交通量并不存在必然的因果关系，而应当考虑多种影响条件，如城市内部道路支干路较多，产生尾气不宜扩散，则将产生较大的尾气排放强度堆积. 而城市外围地区，道路较为稀疏，虽然交通量较大，但尾气排放强度未产生淤积.

4 结论

1) 利用VSP分布模型将交通需求与尾气排放量化计算建立联系，以15 min为预测周期进行交通需求预测得到全路网平均速度等交通流信息，求解机动车比功率，确定机动车比功率在不同速度区间下分布，最后利用标定后的IVE模型计算区域内尾气排放量，为量化尾气排放提供了一种可行的方法.

2) 利用以雷达检测器采集的交通量作为数据的来源，数据获取简单. 只需满足OD反推的断面数据量即可预测区域内尾气分布，相比于全路段观测，需要较少的断面数据量；通过典型路段选取，确定机动车行驶特征参数，建立网络化尾气模型，提高了尾气排放因子量化精度，同时结合交通需求可以实现尾气排放因子数据的周期预测.

3) 交通检测器点位布设优化，能够影响OD矩阵估计的准确性，进而影响尾气排放预测的准确性. 此外，结合多车型模拟排放因子在大气中的扩散过程，有助于提高机动车污染物的排放测算精度，也是未来的主要研究方向.