混凝土箱梁截面稳态温度场的径向基函数配点法反演

孙维刚， 张筱雨， 秦 煜， 许军才

(1.石家庄铁道大学土木工程学院， 石家庄 050043； 2.长安大学公路学院， 西安 710064；3.中铁二院重庆勘察设计研究院有限责任公司， 重庆 400023; 4.河海大学力学与材料学院， 南京 210098)

在混凝土箱梁温度场分析中，截面内部分测点温度值较为容易测得，但若要仿真整个截面的温度场，需要确定边界条件类型、边界条件参数，如对流系数、环境温度等，其中有些参数难以准确确定[1]. 这类通过已知部分测点温度值来求解边界条件或直接模拟整个截面温度场的问题，可以视作热传导反问题[2]. 解决这种缺省边界条件下的温度场仿真问题，对精确计算混凝土温度场、模拟温度效应，具有一定意义.

无网格法是一种新型的数值分析方法，它避免了网格划分，在解决不规则形式的数值计算方面，具有一定优势. 径向基函数配点(radial basis function collection method， RBFCM)法[3]从某种意义上来说是一种真正的无网格方法. 它与空间维数无关，具有形式简单、各向同性等优点，可以逼近几乎所有的函数[4]. 早期研究者希望用解析方法研究热传导反问题，但是由于实际问题的复杂性和多样性，只有少数问题能够求得解析解. Yu 等[5]研究基于解的反演无网格法，并将其应用于稳态热传导问题的边界温度和对流分布的确定.

无网格方法目前已成为计算科学研究的热点之一，由于对其研究较晚，目前尚未解决的问题较多，对其应用进行研究是非常重要的[6]. 无网格法在工程中有大量应用，取得了一定成效，但是从发展状况来看，对无网格径向基函数配点法的研究重点还处在理论阶段，无网格法主要应用于解决规则的长方形或者不规则的圆形结构问题，在箱梁结构中的应用鲜有报道[3-6]. 因此，结合对无网格径向基函数配点法的理论研究，对混凝土箱梁截面稳态温度场进行分析，针对具体问题，编程对混凝土箱梁温度场进行模拟，实现对混凝土箱梁温度场的反演.

1 二维稳态热传导理论

1.1 热传导方程

二维稳态热传导问题的热传导方程为

(1)

1.2 边界条件

混凝土水化热的边界条件，通常采用第三类边界条件，即采用对流边界条件. 数学表达式为

(2)

式中：Ta为环境温度，℃；β为表面对流系数，kJ/(m2·h·℃)；λ为导热系数，kJ/(m·h·℃).

2 径向基函数配点法

径向基函数法具有形式简单、和空间维数无关、收敛速度快的特点[7]，Franke等[8]比较了20种离散数据插值方法，发现Hardy提出的多二次函数(multiquadrics，MQ)[9]插值精度更高. 逆多二次函数(reciprocal MQ，RMQ)是多二次函数MQ的倒数.

径向基函数是以Euclideam范数r=‖x-xk‖为自变量的函数，记为Φ(r)或者Φ(‖x-xk‖)，式中xk为空间中的场节点(基点).

2.1 径向基函数

定义在全域上的以节点xi(i=1,2，…，N)为中心的径向基函数有[10]

MQ函数

(3)

RMQ函数

(4)

式中ds为支撑域尺寸.

2.2 支持域尺寸

ds计算公式为

ds=c0dc

(5)

式中：c0为该支撑域的量纲一的形状参数；dc为位于计算点附近支撑域内的节点间距.

节点平均间距可以简单定义为

(6)

式中：As为预估支持域的面积；nAs为包含在该面积内的预估支持域中的节点数.

2.3 径向基函数插值

将求解域区域用场节点离散，函数u(x)在域Ω中的近似函数uh(x)可用各场节点xk为中心的径向基函数φi(‖x-xi‖)的线性组合表示为

(7)

式中：ai为待定系数；φi(‖x-xi‖)为MQ函数或RMQ函数.

假设该近似函数uh(x)在给定的离散节点处xi(i=1,2，…，N)与由控制方程和边界条件决定的已知函数值ui=u(xi)相等，从而建立关于系数ai的线性方程组

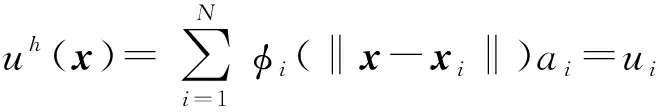
(8)

用矩阵方程表示为

Φa=u

(9)

式中

求解线性方程组，得到系数a. 由于配点法中矩阵u是根据控制方程或者边界条件确定的已知条件，所以a是能够求解的，且不包含未知数.

a=Φ-1u

(10)

将a代入式(7)得到任一计算点的温度场.

3 径向基函数配点法推导热传导方程

将函数u(x)具体化为T(x). 近似函数T(x)可用各场节点xk为中心的径向基函数φi(‖x-xi‖)的线性组合表示为

(11)

3.1 热传导方程

对于二维稳态热传导方程进行无网格法变换，可以表示为

(12)

3.2 边界条件

第三类边界条件的无网格表示为

(13)

将式(13)写成矩阵的形式并合并同类项为

(14)

4 径向基函数配点法数值模型建立

4.1 稳态温度场分析总体刚度矩阵

假设箱梁结构共有N个计算点，其中箱梁内部有n0个计算点，满足第三类边界条件的有n1个计算点，组装相应计算点的方程可得到径向基函数配点法正分析离散系统方程为

Ka=F

(15)

式中的总体刚度矩阵K和总体源向量F的形式为

式中N=n0+n1.

对于反问题，部分条件未知但部分测点的温度值已知，因此，增加附加条件式

(16)

式中：nc表示已知温度值的测点数；右侧fi(x,y)表示测点实测温度值.

此时，求解域内部已知温度值的测点不仅满足控制方程式(11)(12)，而且满足附加条件式(16). 从式(15)(16)求得系数ai并代入式(11)，即可求得稳态温度场.

4.2 误差分析

计算结果的误差通过相对均方根误差(relative root mean square error，RRMSE)体现，计算公式为

(17)

式中：Tj为精确解，本文视有限元解为精确解;Te,j为计算值；P为测试RRMSE的数据数量. 无网格法通过有限测点温度值仿真全截面箱梁温度场，这是有限元法所不具备的功能. 研究目的不是对比无网格法和有限元法在仿真温度场时精度的高低，因此，以有限元法作为反分析结果校核的标准，能相对体现无网格法分析的准确性.

5 箱形截面温度场反演分析

为了研究径向基函数配点法数值模型的实用性，以混凝土箱梁为例，研究表面边界条件缺失情况下的混凝土箱梁温度场反问题.

5.1 问题描述

以某典型混凝土箱形截面为研究对象，其截面如图1所示. 混凝土导热系数λ=10.09 kJ/(m·h·℃)，表面的对流系数均为β=60 kJ/(m2·h·℃). 箱梁顶面边界Γ1：TΓ1=35 ℃；箱梁内表面边界Γ2：TΓ2=20 ℃；其余外表面边界Γ3：TΓ3=30 ℃. 反演分析中，假设右侧腹板边界条件未知，无网格法场节点离散图见图2，有限元法网格划分见图3，温度测点布置见图4.

5.2 结果分析

无网格节点坐标值等于对应有限元网格划分后的节点坐标值，节点离散间距为0.2 m. 配点法计算时，箱梁内部边界和外部边界均采用对流边界条件. 节点离散如图2所示. 分别对比采用RMQ和MQ函数的配点法的计算结果. 计算不同c0下的RRMSE，见图5.

从图5中可以看出，当c0在0.5～9.0范围内，形状参数c0和RRMSE形成近似二次曲线型关系，MQ配点法的RRMSE曲线更为规则，RRMSE的最大值在范围的两端，RRMSE变化明显，而RMQ配点法的RRMSE曲线规则性不强，较为平缓，并且在c0=0.8～0.85时，RRMSE骤降.

MQ配点法在c0=5时，RRMSE最小，为0.003 92. RMQ配点结果在c0=3.5时，RRMSE最小，为0.003 44，表明采用RMQ配点法的正算效果优于MQ配点法.

反演时，由于域内有已知的节点温度值，因此，正分析中由控制方程离散的实测点处的温度场方程，转化为温度场已知的离散方程. 分别对比采用RMQ和MQ函数配点法的计算结果，计算不同c0下的RRMSE，见图6.

从图6中可以看出，MQ配点法下，在c0=3之前，RRMSE稳定，当c0=3.5时，RRMSE突变，在c0=4.5之后，RRMSE又出现震荡，当c0=4.5时，RRMSE最小，为0.013 21. RMQ配点法下，在c0=3.5之前，RRMSE稳定，当c0=4.0时，RRMSE突变，当c0=2.0时，RRMSE最小，为0.006 872. 表明采用RMQ配点法的反演效果优于MQ配点法.

以上分析表明，有限元和径向基函数配点法的计算结果吻合度较高. 基于径向基函数配点法，在部分边界条件缺失的情况下，能将测点实测温度值作为已知的附加条件，直接代入径向基函数配点法离散矩阵，求出待定系数向量，进而确定整个截面的温度场，可以避免求解边界对流条件，克服部分边界条件未知导致的温度场仿真困难.

6 结论

文章推导并建立混凝土箱梁截面稳态温度场正反分析的径向基函数配点法模型，并将该模型应用于混凝土箱梁截面稳态温度场的计算中.

1) 对于箱形截面稳态分析，正算中，当c0为0.5～9.0，c0和RRMSE形成近似凹曲线型关系，采用MQ和RMQ函数的配点法求得的温度值和有限元结果的RRMSE存在最小值.

2) 反演中，MQ函数配点法下，在c0=3之前，RRMSE稳定，当c0=3.5时，RRMSE突变，在c0=4.5之后，RRMSE又出现震荡，RRMSE存在最小值.c0-RRMSE曲线为震荡型凹型线.

3) 采用径向基函数配点法计算的温度值和有限元法计算的温度值在箱梁截面的对应节点上差值较小，吻合度较高. 采用RMQ配点法的正算和反演效果均优于MQ配点法.

4) 径向基函数配点型无网格法可以避免求解边界条件，克服边界条件缺失对仿真温度场的限制，为提高箱梁温度场仿真精度提供便捷的方法.