基于一维波动理论的特厚覆盖层坝基动力特性研究

余 挺，邵 磊

（中国电建集团成都勘测设计研究院有限公司，四川省成都市 610072）

0 引言

在覆盖层上建高土石坝，若地基在地震工况下保持稳定或经工程措施处理后能够保持稳定，则建坝就具有可行性。天然覆盖层地基地震动力反应分析是判断其动力稳定性的基础。

运用传统地震动一致性输入方法（刚性边界+惯性力法）进行大坝动力反应分析时，需考虑坝体近域地基和远域地基的影响，一般将临近坝体地基的河床与山体划分为近域地基，与坝体一起作为计算分析模型。由于外行波能量具有向远域地基传播的逸散效应，理论上近域地基取的范围越大计算精度越高[1]，但存在网格数量庞大、模型复杂，计算工作量不经济等局限，导致工程实用性差。若近域地基范围取的偏小，且采用固定边界，则远域地基耗散的外行波能量将从边界反射回坝体和近域地基内，导致大坝地震响应计算结果失真。

在目前的土石坝动力分析中，对与坝体直接建在基岩上或坝基覆盖层较浅的情况，一般选取基岩面做为模型边界；对于坝基为深厚覆盖层或基岩条件较为复杂的情况，则取向下一定深度和两岸一定宽度区域的覆盖层或基岩作为大坝计算模型的近域地基，并做固定边界处理，对坝体施加惯性力，在边界处输入地震加速度[2]。这种计算方法就像是将整个计算模型放在刚度很大的振动台上，整个系统是能量封闭的。计算分析研究表明[3]，固定边界条件的计算结果在量值上与较合理的计算结果（波动输入方法）相差高达20%，且与坝体体积和地基变形模量密切相关，已不能很好地适应厚达数百米级覆盖层上高土石坝的抗震计算要求。因此，研究将建在深厚覆盖层上的土石坝作为开放系统的波动问题来求解。

一维波动理论是地震工程界较为常用的波动问题求解方法。该该理论假设土体为水平分层，每一水平子层为线黏弹性体，其动剪切模量与阻尼比均为剪应变的函数，通过计算任一子层对地震波输入层的传递函数，来推求土层地表的地震反应，常用于计算覆盖层等天然地基的动力响应[4-8]。岩性地基条件下，将基岩考虑为具有自由边界的弹性半空间，假设上覆土层对基岩内的入射波无影响，而基岩面以下的入射波在基岩内被全部吸收，在计算中取由下卧基岩处向上传播的输入加速度峰值等于露头基岩场地表面设计地震加速度的二分之一，则基岩面的加速度即可达到设计值[9-11]。但针对存在天然覆盖层的非岩性地基，考虑覆盖层与基岩相互作用以及覆盖层土体本身的强非线性动力特性，使得在覆盖层与基岩的接触面处，基岩内竖直向上的入射波并不等于向下返回基岩内的反射波，即基岩内入射波在覆盖层土体与基岩的接触面处不可能等于覆盖层不存在时的输入地震波的一半[12]。故在计算地震波输入层的传递函数时，还应考虑覆盖层与基岩的相互作用。

有研究表明[13]，是否考虑覆盖层与基岩的相互作用，对于动力反应时程、加速度峰值及反应谱的影响均不可忽视。若不考虑覆盖层与基岩与的相互作用，计算得到的动力反应偏小，使得抗震设计趋于不安全。故此，本文根据文献[13]考虑基岩与上覆土层的相互作用的方法，计算了500m级特厚覆盖层坝基系统的一维土层地震反应。

1 计算方法与参数

1.1 基本理论[13]

在一维波动理论中，将自由场地地震运动过程简化为垂直向上传播的一维剪切波，产生的水平位移可以表示为：

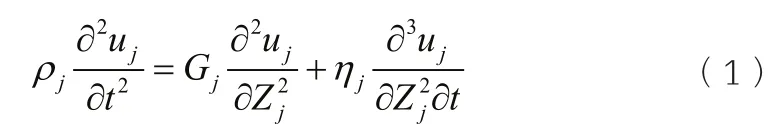
式中：ρ——质量密度；

G——剪切模量；

η——黏滞阻尼系数。

黏滞阻尼系数η可由粘滞阻尼比β表示为：η2Gβ/ω=。为第j层土中Zj处的水平位移。

在频域中，可以将地震波化为若干简谐波，其中一条的运动方程可表示为：

将式（2）代入式（1），可得：

式中：

式中：kj——第j层的复波数；

vj——复剪切波速；

——复剪切模量。

G和β是频率的函数，工程上通常取为常数，则可定义复剪切模量：

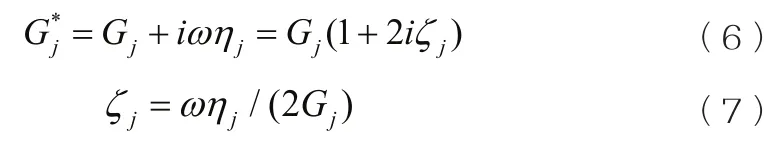
式中：jζ——临界阻尼比。

由式（3）可以看出，介质中某一点的运动Uj由两部分组成。第一部分是向上传播的波动，表示的是向下传播的波动。其中Ej和Fj分别表示振动幅度的大小，称为波幅系数。

在相邻界面上的剪应力和位移连续条件下，可得如下递推关系：

式中：hj——第j层土的厚度；

aj——第j层土的复阻抗比，与频率无关。

如果从第j层的顶面输入位移幅值为的地震动，第m层顶面的位移反应为则第m层对第j层的位移传递函数为：

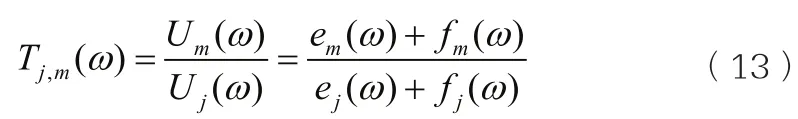
当地震动从基岩顶面输入时，假定基岩以上土层对基岩内的入射波无影响，基岩面以下的反射波在基岩内全部吸收。即基岩内入射波和反射波幅值之间，在基岩顶面处存在关系：（带′表示不考虑基岩和上覆土层相互作用），从而第m层对于基岩的位移传递函数为：

上述假定是建立在把基岩以上全部土层去掉，基岩面变成半无限空间的自由边界，基岩内的入射波到达自由边界时被完全反射。现行工程上通常采用的一维波动理论即是采用该简化原理进行计算。

实际上由于上覆土层与基岩的相互作用，土层与基岩的入射波和反射波形成了复杂的系统，在基覆界面处，基岩内的反射波和入射波并不相等。故此，有学者[13]给出了传递函数公式为：

1.2 大坝与河床覆盖层参数

规划中的某水电站挡水建筑物采用土质心墙堆石坝，建基面最低高程为2930m，正常蓄水位3070m，死水位3015m，坝顶高程为3080m，最大坝高150m。坝址区河床覆盖层最大厚度达550m，按其物质组成、层次结构、成因、形成时代和分布情况等，自上而下（由新至老）可划为6层，其中，③～⑤层为软弱土层，厚度约240m。第①层由块碎石土及含砂的块碎砾石土组成，厚约130m；第②层由含（块）碎（卵）砾石砂层，粒径大小悬殊，分选性差，级配不良，粗颗粒未形成骨架，厚约160m；第③层以含砾中粗砂、中细砂为主，分布连续；第④层为粉质黏土层；第⑤层以含砾粗砂、中砂、细砂为主，分布连续，厚度较大；第⑥层以砂卵砾石层为主，局部分布有灰黄色粉土、细砂层，厚约20m。各土层剪切波速、动剪切模量、动剪切模量和阻尼比等参数见表1。

表1 计算参数表Table1 Table of calculation parameters

1.3 地震等级

中国地震局地球物理研究所根据相关标准[14]与坝址区工程地质条件，得到坝址区50年超越概率10%地震动峰值加速度为0.20～0.30g，对应地震基本烈度为Ⅷ度。设计加速度代表值的概率水准，对壅水建筑物应取基准期100年内超越概率2%。根据工程场地所处的区域工作背景与地震地质环境，结合工程经验判断，此设计概率下的场地基岩地震动参数水平一般在0.5g以上。

1.4 输入地震波

在场址区附近对工程场地地震危险性贡献最大的主要潜源区见表2所示。

表2 主要潜源对坝址峰值加速度贡献率近似值表 （50年超越概率10%）Table 2 An approximate table of the contribution of main potential sources to the peak acceleration of the dam site

通过地震危险性概率分析，坝址50年超越概率10%的基岩水平峰值加速度为258.8gal，100年超越概率2%的基岩水平峰值加速度为528.9gal，100年超越概率1%的基岩水平峰值加速度为624.0gal。

输入地震波采用100年超越概率2%的场地谱人工地震波，水平向加速度峰值为0.55g，竖向加速度峰值为水平向的2/3，场地谱人工地震波如图1所示。

图1 场地谱顺河向水平加速度时程Figure 1 The site spectrum along the river horizontal acceleration time history

2 计算结果分析

2.1 加速度放大倍数

在场地谱地震波输入作用下加速度放大倍数沿覆盖层深度分布如图2所示。可见在场地谱地震波作用下，覆盖层放大倍数随高程呈现出先减小后增大的趋势。考虑和不考虑基岩-上覆覆盖层相互作用条件下，顶部自由表面放大倍数分别达到0.625和0.536，相差约16%。在软弱土层为主的③～⑤层，地震动出现较大的衰减。

为了对比分析考虑基岩-上覆覆盖层相互作用的影响，根据式（14）和式（15）分别计算了具自由边界基岩工况与基岩-土层相互作用工况下的位移传递函数。图3显示了两种情形的位移传递函数的幅值比，可以看出前一种情形的传递函数之幅值，总是小于（不超过）后一种情况下传递函数的幅值。相对应的，覆盖层顶部的峰值加速度小于考虑到基岩与上覆土层存在相互作用时的结果。

图2 加速度放大倍数沿覆盖层深度的分布图Figure 2 The distribution of acceleration magnification along the depth of the overburden

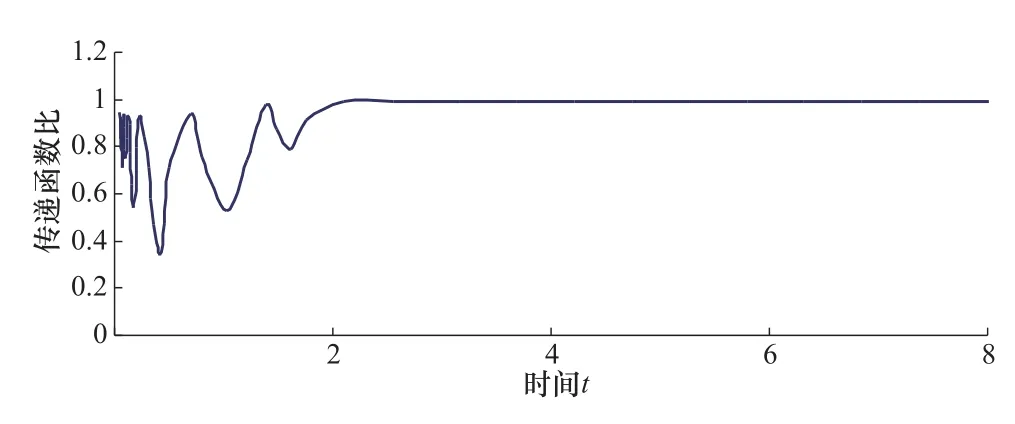
图3 具自由边界基岩工况与基岩-土层相互作用工况之传递函数比Figure 3 Transfer function ratio between free boundary bedrock and bedrock-soil interaction

2.2 考虑覆盖层天然地基上新加土层

为了考虑天然覆盖层地基上筑坝的情况，在原有概化一维土层模型的基础上，新加一层50m厚的堆石材料。新加层参数如下：剪切波速根据文献[15]表7.2建议的土石坝平均剪切波速Vs=300m/s，最大动剪切模量Gdmax=0.89GPa，密度=2180 kN/m3，厚度=50m，λmax=0.254，k1=26。计算结果与天然覆盖层地基对比见图4。

图4 加速度放大倍数沿覆盖层深度的分布Figure 4 The distribution of acceleration magnification along the depth of the overburden

考虑基岩-上覆覆盖层相互作用的一维波动理论计算结果表明，地震波从基岩输入，在覆盖层中的传播模式为土层中减小，至顶部自由面增大，且顶部自由表面的放大倍数小于1。新加层情况下（550m原有天然覆盖层地基+50m新加上覆土层），相当于增加了覆盖层厚度，顶部加速度放大倍数由天然覆盖层地基（550m）的0.625减小为0.536，减少了14%，可见随着高度增加（针对高度500m以上情况），建基面地震动的放大效应呈现逐渐减小的趋势。取同一水平截面的建基面（550m高度处）对比来看，新加层情况下，放大倍数由0.625减少为0.418，减少约33%，说明上覆结构对建基面影响较大。这一结论不一定适用于覆盖层上筑坝，因为坝体结构和覆盖层相比很小，类似于一根筷子，地震波顺着坝体传播上去，坝顶会产生鞭梢效应。另外，以上两种情况，软弱土层③～⑤的滤波效应均较为明显。

2.3 覆盖层自由表面加速度

图5示出在基覆界面处输入场地谱人工波时，覆盖层顶部表面的地震响应，其对应的加速度反应谱示于图6。

图5 覆盖层顶部自由面加速度时程Figure 5 Time history of overburden surface acceleration

图6 覆盖层顶部自由面加速度反应谱Figure 6 Acceleration response spectrum of overburden surface

可见，通过对比计算是否考虑基岩-覆盖层相互作用两种工况算出的覆盖层顶部表面的动力响应，无论加速度峰值还是其谱特征均有差异。与图4对应的位移传递函数相比较，在不考虑基岩-覆盖层相互作用工况下，覆盖层顶部表面的动力反应的峰值加速度和反应谱峰值均偏小。

3 结论

本文采用考虑基岩-覆盖层相互作用的一维波动理论，对强震区特厚覆盖层坝基进行动力反应分析，得到以下结论：

（1）峰值加速度为0.55g的地震波从基岩输入，在含软弱土层的500m级特厚覆盖层中的传播模式为入射后先衰减，至顶部自由面增大，且顶部自由表面的放大倍数小于1。传播过程中覆盖层所含的软弱土层滤波效应明显。

（2）考虑和不考虑基岩-覆盖层相互作用，顶部自由表面放大倍数分别达到0.625和0.536，相差约16%，后者缩减了土层的放大效应。

（3）上覆结构对建基面影响较大，随着建筑物高度的增加，覆盖层建基面地震动的放大倍数呈现逐渐减小的趋势。