基于饱和多孔介质PSBFEM的闸坝—可液化地基动力响应分析
2020-03-21邹德高刘京茂滕晓威
邹德高,陈 楷,陈 涛,王 锋,刘京茂,滕晓威
(1.大连理工大学水利工程学院,辽宁省大连市 116024;2.大连理工大学海岸和近海工程国家重点实验室,辽宁省大连市 116024;3.四川华能泸定水电有限公司,四川省成都市 610072;4.中国电建集团成都勘测设计研究院有限公司,四川省成都市 610072)
0 引言
随着中国水能资源开发工作不断深入,近年来水利工程选址地质条件复杂,深厚覆盖层上建坝难以避让[1]。中国已建的多布、丹巴、江边、打鼓滩等闸坝结构底部均存在一定厚度的覆盖层地基土,地震作用会导致土层弱化,将对上部结构安全构成一定的潜在威胁。相关学者针对不同工程特点开展了研究,如姜云龙等[2]研究了打鼓滩闸坝的应力变形特征;王登银等[3]分析了闸坝静力特性和基础处理效果;段斌等[4]研究了闸坝基础加固处理方案,并对比了不同方案的效果;任苇等[5]开展了巨厚覆盖层上高闸坝沉降控制关键技术研究,建议了相关标准参数。王刚等[6]基于对比应力法和动力反应分析,进行了某闸坝地基液化判别应用。
现有的研究大多未考虑覆盖层中存在可液化土层的情况,而地震可能诱发的覆盖层液化现象对于结构和机组的抗震安全具有更加重要的控制作用。但有关上部闸坝结构与可液化覆盖层地基土体系动力反应的研究成果还很少。
本文采用高效四分树[7]方法建立闸坝—可液化地基体系的跨尺度分析模型,通过饱和多孔介质多边形比例边界有限单元[8]联合土体广义塑性模型,模拟地基孔隙水压力的产生、扩散和消散过程,开展了考虑覆盖层液化的闸坝结构动力反应分析,讨论了地基孔隙水压力、孔压比分布规律及闸坝变形模式。
1 PSBFEM饱和土动力分析方法
多边形比例边界有限元(PSBFEM)[9]放松了对单元形状的限制,具有非常好的灵活性,且复杂边界适应能力强[10][11],已广泛应用于动力相互作用分析[12]、接触分析[13]、裂纹扩展分析[14-16]、复杂单元求解[17]、非线性材料分析[18-23]等方面,理论成熟,具有较好的应用潜力,故本文基于前期研究,进一步将该方法推广到饱和地基土的液化分析。
1.1 孔压场函数
多边形比例边界有限单元理论已有多篇文献给出详细介绍[9][10][18],本文重点给出用于液化分析的关键方程,任一点的孔压可用比例边界坐标表示见式(1)、(2):

式(3)为关于ξ的二阶非齐次常微分方程,其中和为只和渗透系数和几何形状有关的系数矩阵为节点流量向量。
对任一多边形,方程(3)的解为式(4):

将式(4)代入式(1)便可求得多边形内以边界节点孔压表达的孔压场函数见式(5):
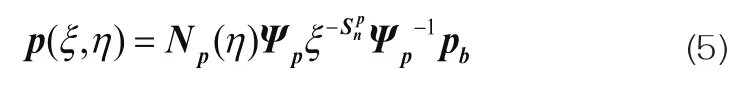
1.2 应变和流速转换矩阵


上述理论方法已集成到大连理工大学工程抗震研究所自主开发的大型岩土工程非线性分析软件GEODYNA[24],本文采用该软件开展后续计算研究。
2 闸坝与可液化地基体系的动力反应分析
2.1 计算模型
图1给出了闸坝与可液化地基体系的几何尺寸示意说明,图2为采用四分树离散方法快速生成的有限元分析模型(砂土层为可液化土层,A、B、C、D为观测代表点),其中离散最小尺寸设定为1.0m,最大尺寸为8.0m,模型共生成单元数5975,节点数6363。该方法可实现网格尺寸灵活、快速跨越,既可保证防渗墙等易发生应力集中的部件采用精细网格,又可限制整体单元量,节省计算资源。
2.2 计算参数
混凝土结构采用线弹性模型,土体采用广义塑性模型,土-结构界面采用弹塑性接触面[25]模拟,参数列于表1~表3,考虑中间砂土层液化,其渗透系数取为5×10-4m/s。静力计算考虑了地基土层初始应力、闸坝的分期填筑和蓄水过程。
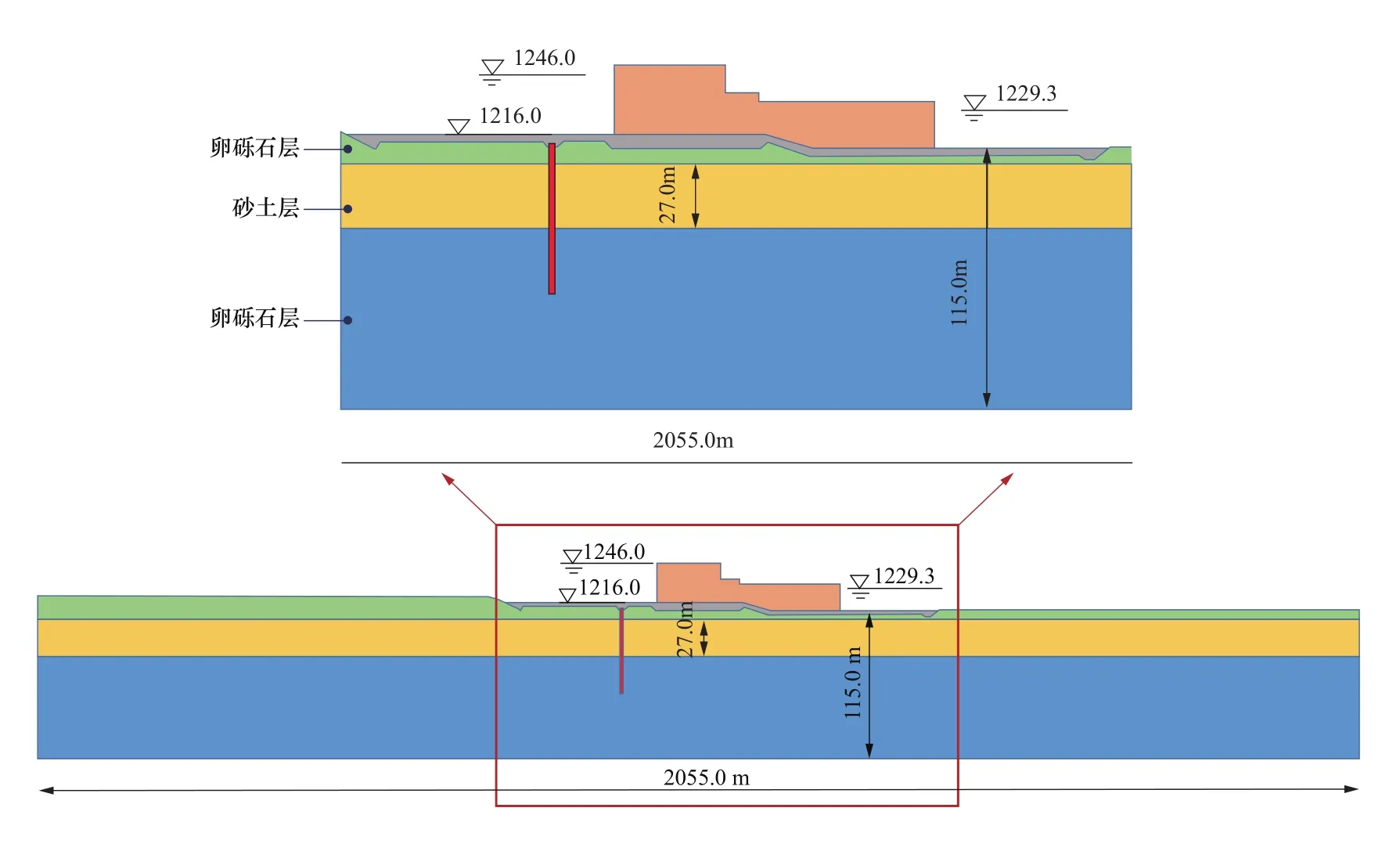
图1 闸坝与可液化地基体系的几何尺寸信息示意说明Figure 1 Illustration of geometric dimension information

表1 地基土广义塑性模型参数Table1 Generalized plastic model parameters of soil material

表2 广义塑性接触面参数Table 2 Parameters of the generalized plastic interface model
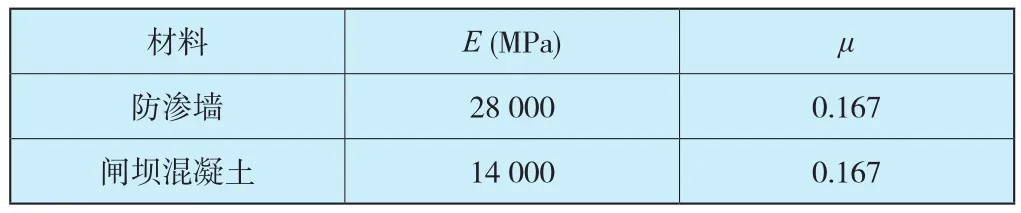
表3 线弹性材料参数Table 3 Parameters of linear model
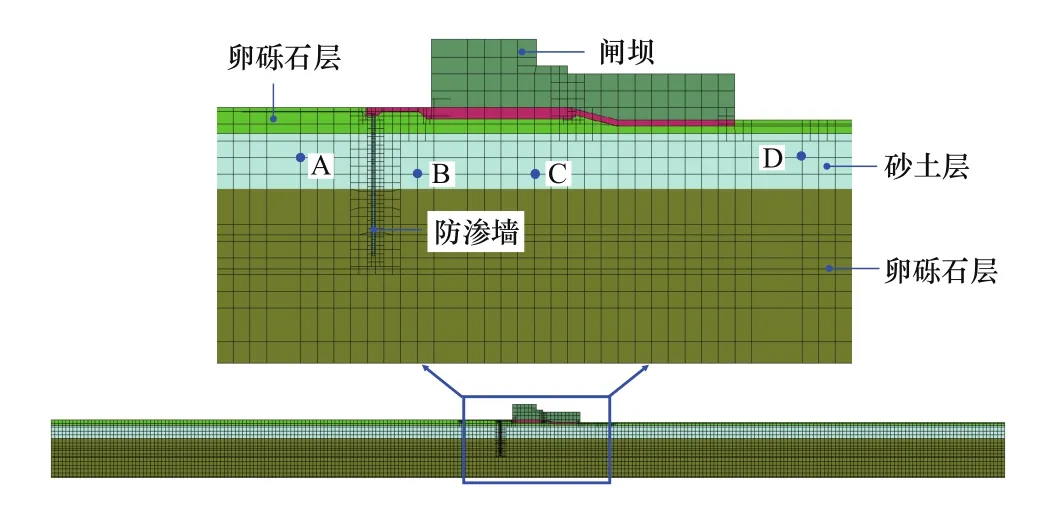
图2 四分树离散的闸坝与可液化地基体系的有限元模型Figure 2 Finite element model of sluice dam using quadtree
动力计算中,采用规范谱人工波,水平向峰值加速度取0.2g,图3给出了时程曲线,持时长为30s,计算时间步长取为Δt=0.005s。

图3 地震加速度时程曲线Figure 3 Time history curve of seismic acceleration
2.3 计算结果分析
2.3.1 地基土液化
(1)孔隙水压力。
图4给出了地震作用下土体中孔隙水压力(简称孔压)分布规律。为便于观察,本文仅给出了部分计算域的结果,随土层深度增加,孔压总体呈增大的趋势,其中最大孔压出现在闸坝下方的可液化土层底部,主要是由于闸坝的重力作用在一定程度上改变了下层土体的应力状态。
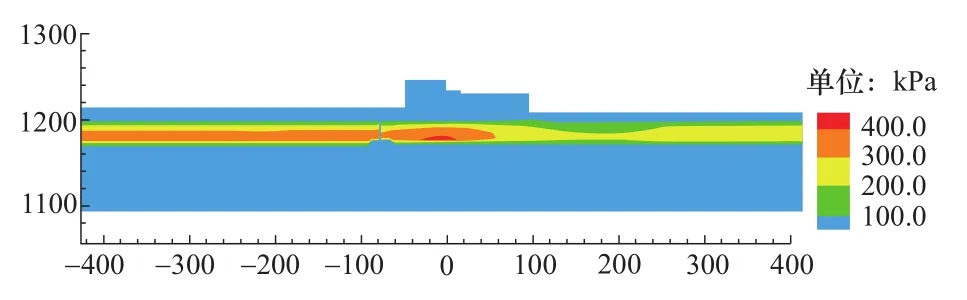
图4 地震作用下土体中孔隙水压力分布Figure 4 Pore water pressure distribution in soil under earthquake
图5列出了四个代表点处孔压在地震过程中的变化规律,可以看出,随地震时间的增加,孔压总体呈持续累积增长的趋势,当地震接近结束时孔压趋于平稳。
(2)孔隙水压力与静力竖向应力比。
通过孔压与地基土静力竖向应力的比值来判别土体液化情况,当比值接近1.0时,认为液化现象明显。图6给出了该比值的分布云图,可以看出:防渗墙周边上游部分土体出现了较为明显的液化,闸坝底部土体液化程度稍小于上游和下游土层,主要原因是闸坝的竖向重力作用,改变了下部土层的应力状态,增加了土体竖向应力,使得孔压比数值相对偏小。

图5 代表点的孔隙水压力时程变化规律Figure 5 Time-history variation of pore water pressure at representative points
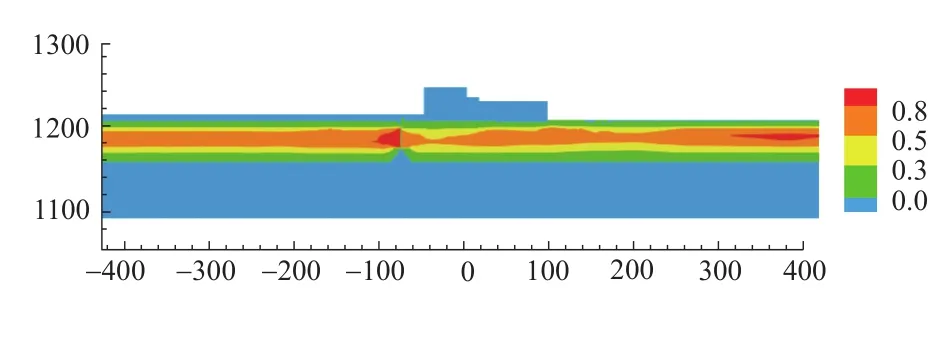
图6 孔隙水压力与静力竖向应力比分布Figure 6 Ratio of pore water pressure and vertical stress in static
2.3.2 结构变形
(1)整体变形。
图7给出了闸坝体系的震后网格变形图,可以看出,由于砂土层部分弱化,使得上部闸坝结构整体呈水平向下游移动,最大水平向位移为33.4cm,并伴有略微向下游倾斜的趋势。
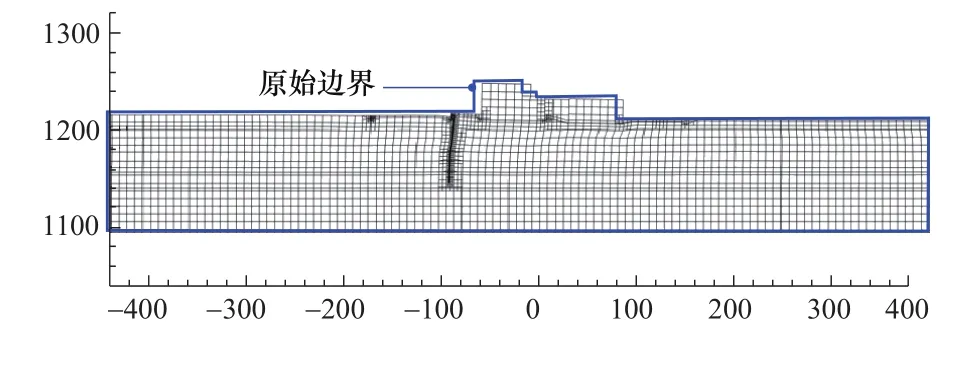
图7 震后闸坝体系整体变形(放大20倍)Figure 7 Overall deformation of sluice dam system after earthquake (Magnify 20 times)
(2)防渗墙变形。
图8绘制了防渗墙位移随高程变化的分布和整体变形轮廓,可以看出,结构顶部最大水平向位移为30.4cm,底部变形很小,故防渗墙受弯作用较为明显。

图8 震后防渗墙位移与变形Figure 8 Displacement and deformation of cut-off wall after earthquake
3 结论
本文首先通过高效四分树方法建立了闸坝-可液化地基体系跨尺度分析模型,而后基于土体广义塑性模型和弹塑性接触面模型,通过饱和多孔介质多边形比例边界有限单元方法,计算了覆盖层中存在可液化土层情况下闸坝的动力响应,同时模拟了地基土中孔隙水压力的产生、扩散和消散过程。计算结果表明:
(1)闸坝底部土体液化程度低于上下游地基土,主要是由于闸坝自重的竖向作用在一定程度上改变了底部土体的应力状态。
(2)地震致使部分土层弱化,使得闸坝整体向下游水平移动,最大变形为33.4cm,并略有向下游倾斜的趋势;防渗墙沿水平向变形明显,顶部最大位移为30.4cm,底部变形较小,应结合实际工程情况,采取适当的加固措施,避免影响机组安全运行。
(3)本文方法准确,且适应性强,为地基抗液化措施的对比与验证研究提供了可靠的技术支持。同时具有较好的应用潜力,易于拓展至三维和其他复杂结构的地震响应分析。
