冻融循环作用下砂岩蠕变特性及损伤模型研究*

陈国庆 万 亿 裴本灿 米冠宇

(地质灾害防治与地质环境保护国家重点实验室(成都理工大学)， 成都 610059， 中国)

0 引 言

青藏高原高寒地区基础设施建设和运营过程中，不乏岩体长期稳定性问题，而岩石流变性作为反映岩体长期稳定性的基本标准，往往与公路边坡失稳，桥梁基础沉降及隧道围岩变形等息息相关。目前，岩石流变以蠕变为主研究较为广泛，而研究方法以蠕变试验、本构模型及数值分析等进行岩石流变学理论的搭建。其中，试验是建立本构模型的基础，试验的设计及结果决定了本构模型的形态，大量学者基于不同的试验条件研究了适用于该环境下的本构模型(陈卫忠等， 2009； 张清照等， 2012； 康文献等， 2016； 赵延林等， 2016； Wu et al.， 2017； 丑亚玲等， 2018; 陈昌富等， 2019； 蔡国军等， 2019)，而数值分析作为沟通本构模型与数据的桥梁，其反演方法也对本构模型可靠性判别起关键作用(陈炳瑞等， 2005； 黄书岭等， 2008)。

近几年来，考虑温度损伤效应的岩石蠕变及本构模型成为多场耦合作用下岩石蠕变劣化特征研究的热点之一，胡其志等(2009)与朱元广等(2011)对温度影响下的岩石蠕变损伤演化过程进行了详细研究，并基于损伤力学建立了考虑温度损伤的岩石蠕变本构关系； 冻融循环作为一种动态温度损伤效应，同样对岩石蠕变具有一定影响，因此，相关学者(江宗斌， 2016； 陈国庆等， 2017； 童庆闯， 2017； 张峰瑞等， 2019)对经历不同冻融循环次数的砂岩、泥岩与花岗岩等进行了一系列蠕变试验，从不同角度分析了冻融循环对岩石蠕变特性的影响规律，其试验结果均表明冻融对岩石蠕变具有明显的劣化效应，具体表现为在相同应力加载路径下，蠕变变形量随冻融循环次数的增加而增加，而蠕变时长、峰值应力及长期强度等随之降低； 研究指出，冻融循环次数的增加使得岩石软化，导致其强度降低而延性增加，在长期受荷条件下呈现出明显的损伤特征。

然而，现有的研究对于冻融岩石蠕变特性主要分析了冻融循环对岩石宏观长期力学性能的劣化响应，而细化阶段分析及损伤模型构建还有待进一步提升。鉴于此，本文通过对冻融循环后石英砂岩及红砂岩单轴蠕变试验结果进行分析，深入讨论冻融循环对砂岩各蠕变阶段的损伤效应及冻融循环对砂岩蠕变破坏形态演化的损伤机制。在此基础上，构建考虑冻融损伤的西原模型，并结合冻融后红砂岩蠕变试验数据验证模型的正确性，借此揭示蠕变特征参数随冻融损伤程度的变化规律。研究成果表明，冻融循环改变了砂岩蠕变过程中的黏弹塑性变形行为。

1 冻融作用下砂岩蠕变特性分析

1.1 冻融对石英砂岩蠕变特性的影响

一般而言，岩石蠕变可分为3个阶段：衰减蠕变、稳定蠕变与加速蠕变。衰减蠕变阶段岩石应变呈上凸形增长，为应变率由大变小的弹性变形； 稳定蠕变阶段岩石应变呈线性增长，为应变率恒定的弹塑性变形； 加速蠕变阶段岩石应变陡增，为应变率急剧增加的塑性变形。

通过对以往的研究中(陈国庆等， 2017)关于不同冻融循环后石英砂岩蠕变试验结果进一步细化阶段分析可以发现，冻融作用对岩石蠕变的影响不仅限于对其宏观长期力学性能上的弱化，还涉及到岩石各蠕变阶段的时效变形行为，具体表现在：(1)在非屈服应力条件下随着冻融循环次数的增加试样经历的衰减蠕变时长逐步降低，而瞬时与稳定蠕变变形量增加，对应蠕变速率增大； (2)在屈服应力条件下，岩石进入加速蠕变阶段的应力阈值随着冻融循环次数的增加逐渐降低，从稳定蠕变到加速破坏所经历的时间更短，对应应变增量更大。总之，冻融循环对岩石各蠕变阶段具有明显的损伤效应。

因此，在分析冻融后石英砂岩蠕变劣化特征的基础上，为进一步说明冻融循环对砂岩蠕变的损伤效应，本文开展了冻融循环后红砂岩单轴蠕变试验。

1.2 冻融后红砂岩单轴蠕变试验及结果分析

1.2.1 试样制备

试验所采用的红砂岩取自单一岩层较为均质的岩块，表面无明显节理，为细砂状结构。严格按照国际岩石力学学会(ISRM)试验规程将红砂岩制备成直径50imm，高100imm的标准岩样，并要求制备岩样误差不大于0.3imm，两端不平行度不大于0.05imm。加工完后选取完整性较好的岩石进行声波测量，通过测定试样的波速进一步筛选均一性较好的试样进行试验。在本次试验中共选取了15个岩样，分为5组，每组3个。试验前将红砂岩试样放入真空抽气饱和装置内进行强制饱水，待试样完全饱和后测定其饱和质量以确定饱和含水率。岩样的基本物理参数平均值如表1所示。

表1 试样基本物理参数Table 1 Basic physical parameters of red sandstone

1.2.2 试验方案

图1 YSJ-01-00岩石蠕变试验仪Fig. 1 YSJ-01-00 rock creep experimental apparatus

1.2.3 试验结果分析

通过对冻融后红砂岩蠕变试验数据进行整理，建立了如图2～图4所示的经历不同冻融循环次数后红砂岩蠕变变形及位移速率曲线，其反映了岩石蠕变受冻融循环影响的宏观损伤特征。

图2 不同冻融循环次数后红砂岩蠕变曲线Fig. 2 Creep curves of red sandstone after different freeze-thaw cycles

图3 不同冻融循环次数后红砂岩稳定蠕变速率曲线Fig. 3 Steady creep rate and axial stress of red sandstone after different freeze-thaw cycles

图4 最后一级荷载作用下红砂岩蠕变及位移速率曲线Fig. 4 Creep displacement and rate curves of sandstone under the last load

不同冻融循环后红砂岩稳定蠕变速率与轴向应力关系曲线如图3所示。在相同冻融循环次数下，试样的稳定蠕变率随轴向应力的增加呈上凹形增长，这与一般的岩石蠕变试验现象一致； 随着冻融循环次数的增加，在同一级荷载条件下岩石的稳定蠕变速率明显增长，表明岩石的稳定蠕变率不仅受轴向应力的影响，还与冻融循环次数有关，间接反映出高应力作用下岩石的稳定蠕变速率随冻融循环次数的增加而大幅上涨。

在最后一级荷载作用下，经历60次与90次冻融循环的试样均出现了明显的加速蠕变现象(图4)，通过对比在该阶段下的蠕变及位移速率曲线可以发现：(1)试样在发生塑性流动前累积的应变增量随着冻融循环次数的增加而增加，而从稳定蠕变到加速破坏所经历的蠕变时长随之降低； (2)试样的蠕变位移速率曲线整体呈U形，充分反映出试样在衰减及稳定蠕变阶段其速率从递减到稳定的特征，以及损伤累计表现出塑性区扩展导致蠕变速率从稳定到加速增长的现象，而冻融循环次数的增加使得岩石整体的蠕变速率增大，且在加速蠕变阶段表现得尤为显著。

红砂岩在经历多级加载破坏后，其宏观破坏模式也随冻融循环次数的增加而逐渐演化，如图5所示。在无冻融条件下试样破坏仅有一条贯穿整体的主纵向裂缝，伴随在上下端处形成一纵向次生裂缝以连通主裂缝，而在岩样上部约三分之一处观察到一横向次生裂缝。随着冻融循环次数的增加，纵向及横向次生裂缝逐渐演化，表面裂纹数显著增加，试样端部岩块首先破裂。伴随次生裂纹不断发育，局部呈现出明显的张拉特征，故岩石破裂方式逐步从单一斜剪切破坏过渡为共轭断面拉剪复合型破坏。

图5 不同冻融循环后红砂岩试样宏观破坏图Fig. 5 Macroscopic failure modes of red sandstone after different freeze-thaw cycles

不同冻融循环后红砂岩宏观破坏形态差异显著，其原因归结于： (1)组成红砂岩的矿物成分中含大量黏土矿物，如蒙脱石、伊利石、高岭土和绿泥石等，在冻融循环作用下不同矿物具有不同的冻胀融缩尺度，进而产生的不均匀变形对试样造成了一定损伤并有助于冻融过程中水分的迁移； (2)红砂岩中的水分受冻融作用发生相变，在冻结过程中产生冻胀力对原生孔隙壁进行挤压，融化后又可以自由水的形态进行迁移，再反复对孔隙壁施压并伴随水分迁移产生更大的冻胀力，微观封闭裂缝逐渐在试样内部积累，而在长期受荷条件下，时效性损伤有助于裂缝互相贯通，形成微裂缝网，在低于蠕变屈服强度的条件下试样裂缝的扩展会逐步稳定，而在屈服应力条件下，由于有效面积减小在试样内部形成应力集中效应，应力超出岩石微元体强度，微裂缝网不断发育延伸，最终试样沿主破坏面破裂(图6)。

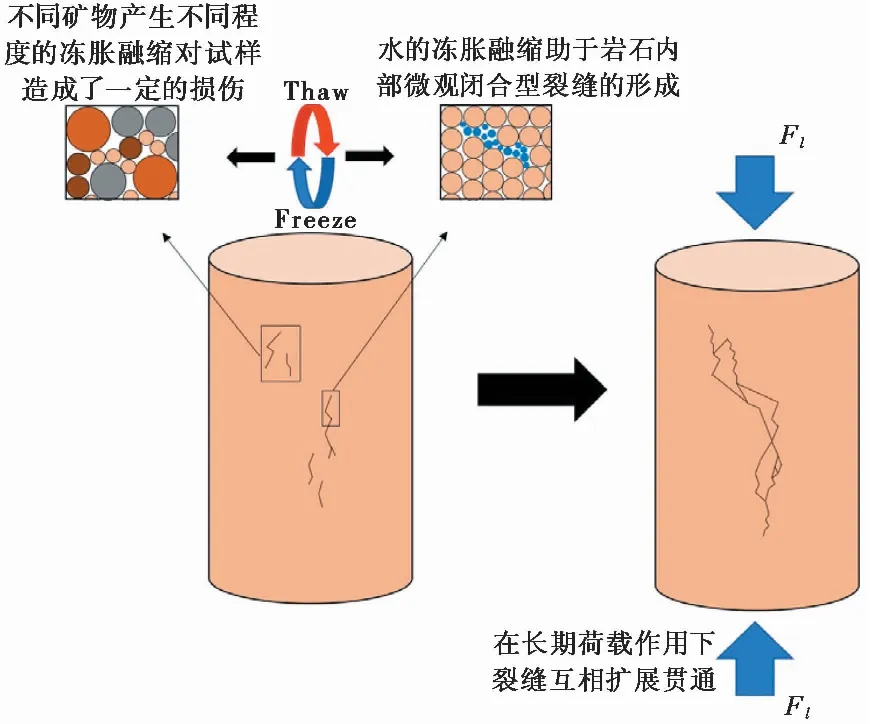
图6 不同冻融循环后红砂岩试样蠕变破坏机理图Fig. 6 Creep failure mechanism of red sandstone after different freeze-thaw cycles

上述试验结果表明，无论是冻融循环后的石英砂岩还是红砂岩，在蠕变试验中均呈现出明显的弱化现象，且冻融损伤涉及到岩石蠕变的各个阶段。为了更深入研究冻融循环对砂岩各蠕变阶段的损伤效应，以下从岩石蠕变本构关系的角度出发，通过构建考虑冻融损伤的蠕变本构模型，进一步量化探讨冻融循环作用下砂岩的蠕变特性。

2 冻融岩石时效损伤本构关系

2.1 冻融损伤系数及长期受荷损伤变量

冻融对岩石蠕变特性的影响可定性化描述为在相同应力路径下衰减蠕变、稳定蠕变及加速蠕变均随冻融对岩石的劣化程度发生变化，而定量化评价其损伤效应则可通过考虑蠕变力学参数随冻融损伤程度变化的非定常性特征来表述，且由于岩石长期受荷引起的疲劳损伤，基于时效性特征的参数本身具有衰减性，故其应宏观上反映冻融与长期受荷的损伤耦合作用。

首先，考虑黏弹性参数具有随冻融损伤程度变化的非定常性特征，即：

E(T)=Ke(T)E0

(1)

η(T)=Kη(T)η0

(2)

式中，E(T)与η(T)为冻融循环T次后的弹性模型与黏性系数；E0与η0为无冻融循环的弹性模量与黏性系数；Ke(T)与Kη(T)分别为弹性冻融损伤系数与黏性冻融损伤系数。

其次，由于岩石是由不同矿物晶体所组成的固态集合体，在长期受荷过程中，微观晶体颗粒间长期力学性质的差异反映出细观损伤的积累具有基于时效效应的随机分布特征，以统计学连续型分布函数表达为：

dD/dt=f(t)

(3)

式中，f(t)为损伤密度函数；D为基于时效效应的长期受荷损伤变量。考虑时效损伤积累为非线性的递增行为，引入双参数的Weibull分布函数定义损伤密度函数，即：

(4)

(5)

式中，θ与λ为长期受荷损伤参数。

黏性系数为冻融环境下的时效性参数，具有时效衰减性与冻融损伤性特征，将其进行长期受荷损伤与冻融损伤耦合，建立如下耦合方程：

η(T，t)=(1-D)Kη(T)η0=Kη(T)η0e-(t/λ)θ

(6)

以上建立的蠕变力学参数具有冻融损伤与冻融长期受荷时效损伤耦合的非定常性特征，将其引入相应的蠕变本构模型中即可建立起描述冻融岩石蠕变的损伤本构模型。

2.2 考虑冻融损伤的西原模型

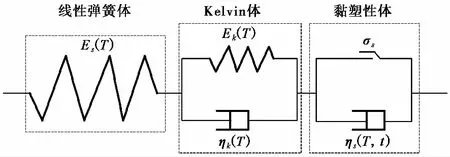
图7 考虑冻融损伤的西原模型Fig. 7 Nishihara model considering freeze-thaw damage

根据串联元件之间应力相等总应变等于各原件应变之和，并联元件之间应变相等总应力等于各原件应力之和，同时考虑元件参数在冻融损伤与长期受荷时效损伤作用下所呈现的非定常性，将E(T)与η(T，t)引入到模型所对应的弹簧体与牛顿黏壶中。由于短时效应的损伤并不明显，考虑冻融时效损伤耦合的黏性系数只引入于描述蠕变加速阶段的黏塑性体中，基此建立如下蠕变损伤本构关系：

(7)

式中，σ1(ε1)、σ2(ε2)和σ3(ε3)分别为弹簧体、Kelvin体与黏塑性体所对应的应力(应变)；Es(T)为线性弹簧体的弹性模量；Ek(T)为Kelvin体中弹簧体的弹性模量，ηk(T)为Kelvin体中牛顿黏壶所对应的黏性系数；ηs(T，t)为黏塑性体中牛顿黏壶所对应的黏性系数，σs为蠕变屈服强度；g(t)为条件判断函数，即：

(8)

式中，ts为岩石加速蠕变起始时。通过求解上述方程关于应变时间的一阶线性微分方程通解，可得到：

(9)

ε(t)即为考虑冻融损伤的西原模型蠕变本构方程。

3 模型验证分析

3.1 模型验证及参数辨识

基于冻融循环后红砂岩单轴蠕变试验数据，采用Levenberg-Marquardt算法对考虑冻融损伤的西原模型进行参数辨识，辨识结果见表2与表3。基于不同冻融循环次数后红砂岩蠕变试验所对应的模型辨识参数，以试验时间为相同自变量建立起模型理论曲线与相同条件下的试验数据进行对比(图8)。为了更直观地反映理论曲线与试验数据的对比结果及冻融循环次数对红砂岩各蠕变阶段的损伤效应，本文仅显示部分冻融循环次数下的模型辨识参数及理论试验对比图。

表2 非屈服应力条件下冻融损伤模型辨识参数Table 2 Parameters of freeze-thaw damage model under non-yield stress

表3 屈服应力条件下冻融损伤模型辨识参数Table 3 Parameters of freeze-thaw damage model under yield stress

图8 红砂岩试验数据与理论曲线对比Fig. 8 Comparison of experimental data of red sandstone and theory curvesa. σ=17.9iMPa；b. σ=35.8iMPa； c. σ=53.5iMPa； d. σ=71.3iMPa； e. σ=89.2iMPa

图8a～图8d为非屈服应力条件下冻融循环次数为0、60及120次的试验数据与理论曲线对比，而图8e为屈服应力条件下冻融循环次数为60及90次的试验数据与理论曲线对比(含加速蠕变阶段)。

通过分析不同冻融循环次数后红砂岩单轴蠕变试验数据，可以得出与冻融后石英砂岩蠕变相同的规律，即：(1)在低于屈服应力条件下，随着冻融循环次数的增加试样更快地进入稳定蠕变阶段，且在稳定蠕变阶段的变形量更大，表明其蠕变速率随冻融循环增加而增加，反映了冻融损伤对岩石的软化效应； (2)在相同屈服应力条件下，试样从稳定蠕变到加速破坏所经历的时间更短，破坏时累计的应变增量更大，反映了冻融损伤对岩石长期力学性能的弱化效应。

从试验数据与理论曲线的对比结果可以看出，考虑冻融损伤的西原模型与冻融后红砂岩蠕变试验数据在任何工况下均有较高的拟合度，表明了模型不仅能描述冻融砂岩在衰减蠕变与稳定蠕变阶段应变呈非线性及线性增长的黏弹性变形行为，还可以反映其在加速蠕变阶段应变从非线性增长到塑性流动的黏塑性特征，且通过对比传统西原模型的理论曲线可以看出改进的模型弥补了传统模型难以准确描述岩石加速蠕变特征的不足。综上所述，在任何应力及冻融循环次数下考虑冻融损伤的西原模型均能与试验数据吻合，即说明了模型的正确性及适用性。

图9 冻融损伤参数拟合曲线Fig. 9 Fitting curves of freeze-thaw damage parametersa. 弹性冻融损伤特征曲线； b. 黏性冻融损伤特征曲线

表2与表3中所示为考虑冻融损伤的西原模型辨识参数，从表中可看出弹性模量及黏性系数均随冻融循次数增加而减小，对应岩石内部力学性质逐渐弱化。为定量描述其衰减特征，求出式(1)、式(2)中的弹性冻融损伤系数及黏性冻融损伤系数关系式，选取其中描述黏弹性特征的参数进行非线性拟合，建立起参数关于冻融循环次数的函数方程。

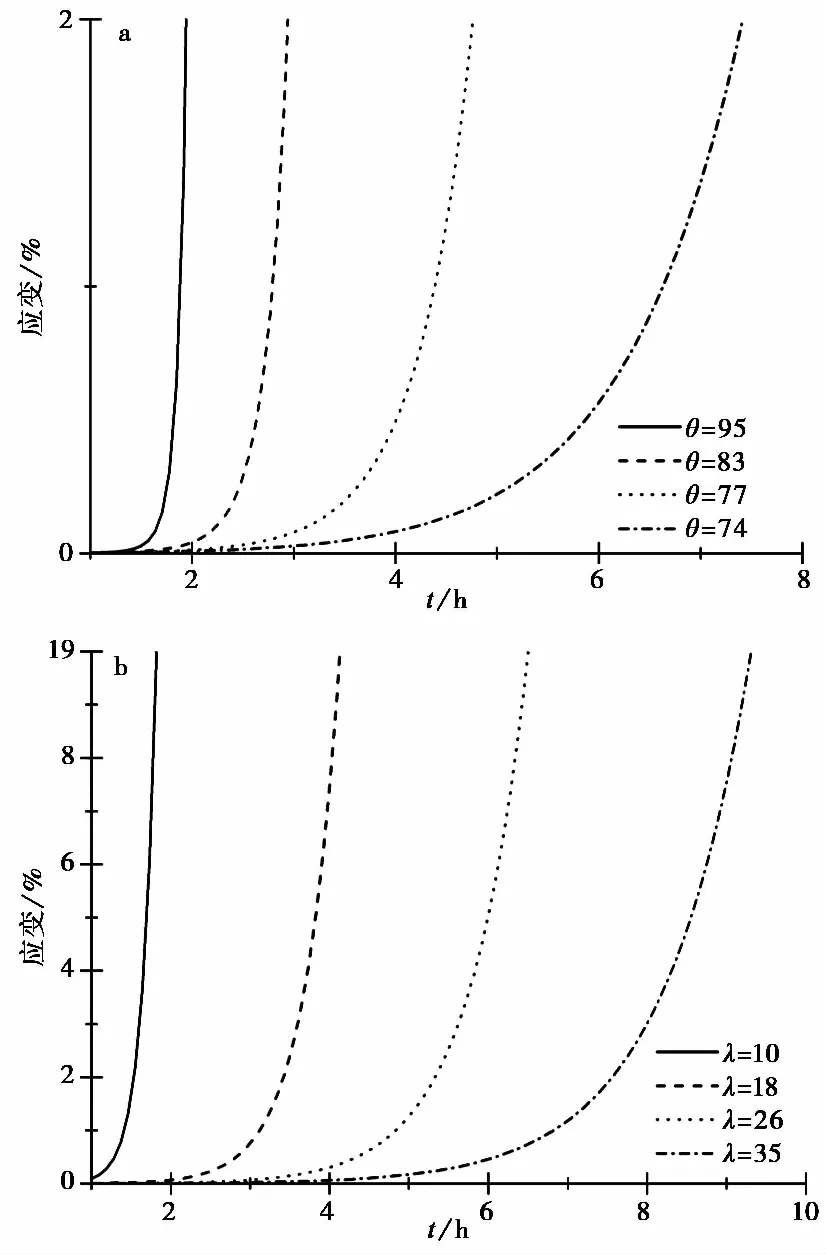
图10 长期受荷损伤参数敏感性分析Fig. 10 Sensitivity analysis of damage parameters under long-term loada. 损伤参数θ； b. 损伤参数λ

3.2 冻融损伤特征参数分析

基于上述考虑冻融损伤的西原模型辨识参数，选取描述岩石蠕变黏弹性变形行为的特征参数，建立起关于Es与ηk参数的损伤系数拟合曲线(图9所示，拟合曲线均满足指数函数关系)。图9a 为弹性冻融损伤特征曲线，其间接反映了岩石蠕变变形中的弹性成分受冻融循环的影响程度，通过拟合函数关系式可以看出，在不同应力条件下弹性损伤系数均随冻融循环的增加而逐渐减小，如果引用关于冻融损伤变量的定义De=1-Ke(张慧梅等， 2010)来描述岩石蠕变受冻融的影响(曲线关于Ke=0.5对称)则可说明其具有损伤扩展型特征。图9b为黏性冻融损伤特征曲线，对比弹性冻融损伤特征曲线则可看出黏性损伤系数随冻融循环次数的增加其下降幅度更为明显，不同应力下曲线均呈凹性下降特征，反映出冻融对岩石蠕变时效流动性的显著影响。

3.3 长期受荷损伤参数敏感性分析

上述建立的西原模型中由于考虑了长期受荷时效损伤效应，引入了关于损伤随机分布特征的Weibull函数，而函数中含有的双参数λ及θ对模型描述岩石加速蠕变起关键作用，故本节通过控制变量法讨论长期受荷损伤参数对加速蠕变阶段的影响规律。

长期受荷损伤参数的分布规律反映了加速蠕变阶段应变随时间递增的非线性变化幅度(图10)。损伤参数θ越大则加速蠕变应变速率越大，岩石内部微观裂缝的累积到宏观断面的产生所经历的时间越短，而λ越小同样对应加速蠕变更为剧烈； 反之θ越小λ越大对应岩石加速蠕变具有明显的时效特征，即应变率随时间而缓慢递增，应变随时间有明显的非线性变化趋势，其机理可解释为：在屈服荷载条件下，岩石内部晶体互相摩擦滑移，不断形成新的受力结构来抵抗外荷载，伴随微观裂缝逐步累积，对应有效面积逐渐减小，产生局部应力集中，周围微观裂缝快速扩展为宏观断面，岩石失稳其应变激增。

4 结 论

(1)经历不同冻融循环次数后的石英砂岩及红砂岩蠕变试验结果表明，砂岩各蠕变阶段均受冻融损伤影响显著，具体表现为：随着冻融循环次数的增加，试样更快从衰减蠕变阶段过渡到稳定蠕变阶段，且对应蠕变变形量及速率均显著增加，而进入加速蠕变阶段的应力阈值逐渐降低，从稳定蠕变到加速破坏所经历的时间更短。

(2)在长期荷载作用下，冻融后红砂岩的宏观破裂形态随冻融循环次数的增加从单一斜剪切破坏模式向共轭断面拉剪复合型破坏模式演化，其破坏机理在于冻融过程中岩石内部微裂隙的发育及时效性损伤促进了微裂隙的扩展和贯通。

(3)将不同冻融循环后红砂岩蠕变试验数据与考虑冻融损伤的西原模型理论曲线进行对比发现，该模型不仅能反映冻融砂岩在衰减蠕变与稳定蠕变阶段的黏弹性变形行为，还可以描述其在加速蠕变阶段应变从非线性增长向塑性流动演化的黏塑性特征。

(4)通过分析冻融损伤特征参数随冻融循环变化的衰减效应及长期受荷损伤参数对加速蠕变的影响规律，得出弹性模量及黏性系数在任何应力条件下均随冻融循环次数的增加而明显下降，且黏性系数的下降幅度更为明显，而长期受荷损伤参数具有控制加速蠕变阶段应变非线性变化的递增幅度。