Submanifolds in Cauchy Riemann Geometry
2020-03-20JihHsinCheng
Jih-Hsin Cheng
Institute of Mathematics,Academia Sinica and NCTS,Taipei 100,China.
Abstract. In this paper I would like to make a report on the results about hypersurfaces in the Heisenberg group and invariant curves and surfaces in CR geometry. The results are contained in the papers [8, 9, 16] and [14]. Besides, I would also report on the results about the strong maximum principle for a class of mean curvature type operators in[10].
Key words: Heisenberg group, umbilicity, Pansu sphere, Strong maximum principle, horizontal (p−)mean curvature, subriemannian manifold, CR geometry, chain, Kropina metric, pseudohermitian geometry, CR invariant surface area functional, singular Yamabe problem, volume renormalization
1 Introduction
We start with a summary of the results. In[8], we defined a notion of umbilicity for hypersurfaces in the Heisenberg group Hnwith n≥2(see Section 2 for some basic material about Hn). We classified umbilic hypersurfaces in some cases, and proved that Pansu spheres are the only umbilic spheres with positive constant p(or horizontal)-mean curvature in Hnup to Heisenberg translations.In[9]we studied immersed,connected,umbilic hypersurfaces in the Heisenberg group Hnwith n ≥2. We showed that such hypersurfaces,if closed,must be rotationally invariant up to Heisenberg translations. Moreover,we proved that, among others, Pansu spheres are the only such spheres with positive constant sigma-k curvature up to Heisenberg translations.
In[10],we studied the strong maximum principle for horizontal(p-)mean curvature operator and p-(sub)laplacian operator on subriemannian manifolds including, in particular, Heisenberg groups and Heisenberg cylinders. Under a certain Hormander type condition on vector fields,we showed that the strong maximum principle holds in higher dimensions for two cases: (a) the touching point is nonsingular; (b) the touching point is an isolated singular point for one of comparison functions. For a background subriemannian manifold with local symmetry of isometric translations,we have the strong maximum principle for associated graphs which include,among others,intrinsic graphs with constant horizontal (p-) mean curvature. As applications, we showed a rigidity result of horizontal (p-) minimal hypersurfaces in any higher dimensional Heisenberg cylinder and a pseudo-halfspace theorem for any Heisenberg group.
In the study of CR invariant curves(called chains) and surfaces(Willmore-type surfaces),we have published the following two papers[14]and[16]. In[14],with the help of a generalization of the Fermat principle in general relativity,we showed that chains in CR geometry are geodesics of a certain Kropina metric in Finsler geometry,constructed from the CR structure. We studied the projective equivalence of Kropina metrics and showed that if the kernel distributions of the corresponding 1-forms are non-integrable,then two projectively equivalent metrics are trivially projectively equivalent. As an application,we showed that sufficiently many chains determine the CR structure up to conjugacy, generalizing and reproving the main result of [6]. The correspondence between geodesics of the Kropina metric and chains allowed us to use the methods of metric geometry and the calculus of variations to study chains. We used these methods to re-prove a result of Howard Jacobowitz that locally any two points of a strictly pseudoconvex CR manifolds can be joined by a chain. Finally, we generalized this result to the global setting by showing that any two points of a connected compact strictly pseudoconvex CR manifold which admits a pseudo-Einstein contact form with positive Tanaka-Webster scalar curvature can be joined by a chain.
In[16],we expressed two CR invariant surface area elements in terms of quantities in pseudohermitian geometry. We deduced the Euler-Lagrange equations of the associated energy functionals. Many solutions were given and discussed.In relation to the singular CR Yamabe problem,we showed that one of the energy functionals appears as the coefficient(up to a constant multiple)of the log term in the associated volume renormalization.
2 Umbilicity and characterization of Pansu spheres
In classical differential geometry, we have the notion of umbilicity for a point in a hypersurface of the Euclidean space Rn. A connected, closed umbilic hypersurface of Rn(i.e., all the points are umbilic) is shown to be a sphere. On the other hand, we have the Alexandrov theorem which says that a closed (compact with no boundary) hypersurface of positive constant mean curvature in Rnmust be a sphere. The original proof of Alexandrov’s theorem is based on a reflection principle. Reflect the hypersurface S across a hyperplane P. Move P parallely until the reflected hypersurface touches the original hypersurface S. The reflected hypersurface must coincide with S by the strong maximum principle. Analytic proofs of Alexandrov’s theorem were given much later. In 1991 Montiel and Ros gave a relatively elementary proof through the characterization of spheres by the umbilicity.
The Heisenberg group Hnis R2n+1,as a set,together with the group multiplication
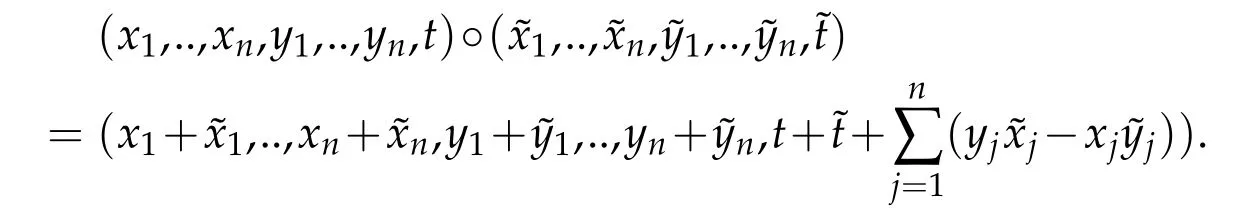
Hnis a(2n+1)-dimensional Lie group. Any left invariant vector field is a linear combination of the following basic vector fields:

The standard contact structure ξ on Hnis the subbundle of THn,spanned by ˚ejand ˚en+j,1≤j≤n.Or equivalently we can define ξ to be the kernel of the standard contact form

The standard CR structure on Hnis the almost complex structure J defined on ξ by

For a hypersurface in the Heisenberg group Hn(see Section 2 of [8] for some basic material),we can still talk about mean curvature,called p(or horizontal)-mean curvature H(see Section 2 of[8]for the definition). A hypersurface defined by such H=0 is called p(horizontal)-minimal. Such p-minimal hypersurfaces or hypersurfaces with prescribed p-mean curvature have been extensively studied in the last ten years.
By analogy with the Euclidean situation, we can ask whether an Alexandrov-type theorem holds for the Heisenberg situation. The reflection principle does not (here and elsewhere)seem to work generally in this situation. In the case n=1,Ritore and Rosales showed that an Alexandrov-type theorem still holds.Their proof relies on the analysis of characteristic curves and singular set developed in[12]. For n ≥2,on the other hand,we may invoke the method of Montiel and Ros to study the Alexandrov-type problem.So the first thing is to characterize,in this case,Pansu spheres(having positive constant p-mean curvature). In[8]we give a definition of umbilicity. We classify umbilic hypersurfaces in some cases,and carry out a characterization of Pansu spheres in Hn.
Let Σ be a C2smooth(further assume the regular part is C∞smooth;see below)hypersurface of the Heisenberg group Hn. Throughout[8], we always assume Σ is immersed and n ≥2.A point p ∈Σ is called singular if ξ=TΣ at p. Otherwise p is called regular or nonsingular(i.e.,ξ is transversal to TΣ). Let SΣdenote the set of singular points,which is a closed subset of Σ.We will further assume the regular part ΣSΣis C∞smooth. For a regular point,we define ξ′⊂ξ ∩TΣ by

Let (ξ′)⊥denote the space of vectors in ξ, perpendicular to ξ′with respect to the Levi metric
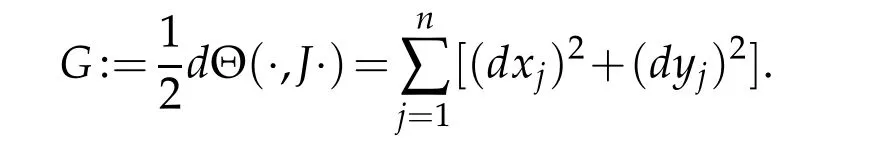
It is not hard to see that dim(ξ ∩TΣ)∩(ξ′)⊥=1.Take en∈(ξ ∩TΣ)∩(ξ′)⊥of unit length.Define the horizontal normal e2n:= Jen. Let ∇denote the pseudohermitian connection associated to (J,Θ) (see Section 2 of [8] for an explanation). Observe that ∇ene2n∈ξ is perpendicular to e2n.So we can write −∇ene2n=lenmodulo ξ′for some function l.Now define the vector field Xn∈ξ′by
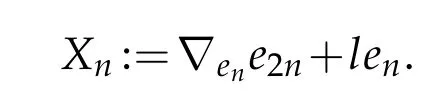
This vector field is uniquely defined on the regular part of Σ.Note that if p∈Σ is a regular point such that Xn(p)=0,then we have

(see Proposition 2.3 of[8])where

Hence we can regard this operator −∇e2n+αJ′originally defined on ξ∩TΣ as an endomorphism on ξ′.Conversely,if ξ′is invariant under the operator −∇e2n+αJ′,then Xn=0.In addition,it is self-adjoint. So we immediately have the following result.
Proposition 2.1. Let p be a regular point of Σ such that Xn(p)=0. There are scalars
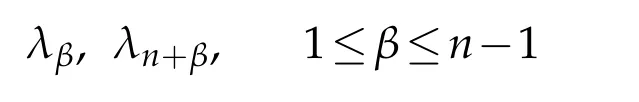
and an orthonormal basis

of ξ′(p)such that
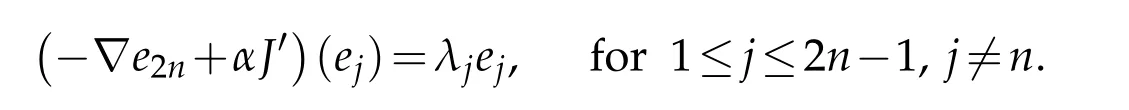
Definition 2.1. A regular point p∈Σ is called an umbilic point if
(1)(−∇e2n+αJ′)(ξ′)⊂ξ′,and
(2)λ1=···=λn−1=λn+1=···=λ2n−1.
If all regular points of Σ are umbilic, we call Σ an umbilic hypersurface of the Heisenberg group Hn. We often use λ(or k)to denote the common eigenvalue in(2)of Definition 1.2.
For any λ>0, the Pansu sphere Sλis the union of the graphs of the functions f and−f,where
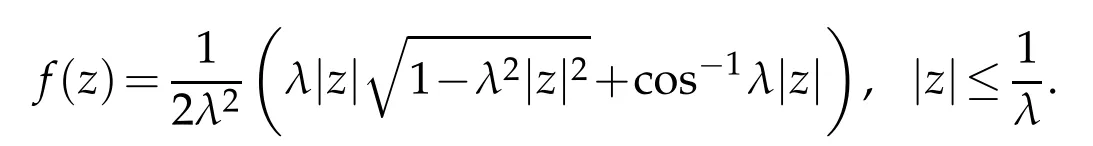
It is known that Sλhas p-(or horizontal) mean curvature H = 2nλ. We say that Σ is congruent to a Pansu sphere if after a Heisenberg translation, Σ coincides with Sλfor some λ>0.
Theorem 2.1. Suppose Σ is a smooth,closed,connected umbilic hypersurface of Hn(n≥2)with positive constant p-mean curvature and nonvanishing Euler number. Then Σ is congruent to a Pansu sphere.
Corollary 2.1. Suppose Σis smooth and homeomorphic to the sphere S2n. Suppose Σ is an umbilic hypersurface of Hnwith positive constant p-mean curvature. Then Σ is congruent to a Pansu sphere.
Note that S2nis closed, connected, and having nonzero Euler number. So Corollary 2.1 follows from Theorem 2.1 immediately.
Theorem 2.2. Suppose Σ is a smooth,closed,connected umbilic hypersurface with l=2k. Then Σis congruent to a Pansu sphere Sλλ=k.
Lemma 2.1. Suppose Σ is a smooth,connected umbilic hypersurface of Hnwith positive constant p-mean curvature,containing a singular point. Then l=2k on ΣSΣ.
Theorem 2.3. Suppose Σ is a smooth, umbilic hypersurface with l=2k. Then k, and hence l, are constant on the whole regular part of Σ. Moreover, if Σ is connected and there exists a singular point p∈Σ,then Σ is either congruent to part of a Pansu sphere or congruent to part of a hyperplane orthogonal to the t-axis.
Theorem 2.2 is an immediate consequence of Theorem 2.3. This is because that If Σ is closed, then it must contain a singular point. Otherwise Proposition 4.5 of [8] would imply that Σ is foliated by geodesics,a contradiction to compactness of Σ. Also the constant l must be positive.On the other hand,Proposition 4.1 of[8]shows that this singular point is isolated,hence Σ is congruent to a Pansu sphere Sλwith λ=k. It was shown that for a rotationally invariant hypersurface in Hnwith l =2k we have the same conclusion as in Theorem 2.3. Note that rotational invariance implies umbilicity.
In Example 3.4 of[8],we introduce two kind of umbilic hypersurfaces with α=0. The hypersurface ΣS2n−1(c)satisfies l=k=. The other one ΣEsatisfies k=l=0. Conversely,we have the following result.Theorem 2.4. Suppose Σ is an umbilic hypersurface with α=0. Then k is a constant on Σ.Moreover, if Σ is connected and k>0, then l=k, and hence Σ is congruent with part of the hypersurface ΣS2n−1(c)with c=. If Σ is connected and k=l=0, then Σ is congruent to part of the hypersurface ΣEfor some hyperplane E.
3 Umbilic hypersurfaces of constant sigma-k curvature
In [8], we studied umbilic hypersurfaces in the Heisenberg group Hn. We proved that Pansu spheres are the only umbilic spheres with positive constant p(or horizontal)-mean curvature in Hnup to Heisenberg translations. See Theorem 2.1 and Corollary 2.1 in the last section.In[9],we want to extend the result to the case of constant horizontal sigma-i curvature.
First let us define horizontal sigma-i curvature of a hypersurface Σ in Hn.Throughout[9], we always assume Σ is immersed (say, C2smooth and C∞smooth in the region of regular points)and n ≥2. In this section, we follow the notions and notation defined in the last section.
We now have a symmetric shape operator S:ξ∩TΣ→ξ∩TΣ,defined by

(see Proposition 2.2 in [8]). A regular point p is called an umbilic point if S(ξ′) ⊂ξ′at p and all the eigenvalues of S acting on ξ′are the same. Let us denote this common eigenvalue by k.On the other hand,by Proposition 2.3 in[8],we have
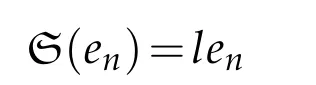
for some real number l. The sigma-m curvature is the m-th symmetric function of the eigenvalues of the shape operator S. For instance,the sigma-1 curvature is nothing but p-(or horizontal)mean curvature H,which is the trace of S.In terms of k and l,we have

at an umbilic point. Similarly the sigma-i curvature,denoted as σi,n,reads
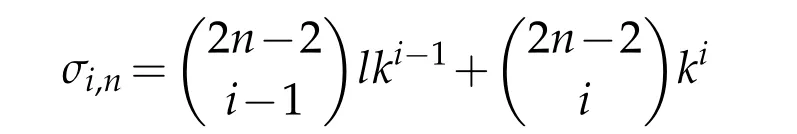
for 1≤i≤2n−2 while

In[8],we study the case i=1,i.e.,σ1,n:=H is a positive constant. Among others,we show that any umbilic sphere of positive constant H in Hn, n ≥2, is a Pansu sphere up to a Heisenberg translation. It is known that the Pansu spheres Sλhas p-(or horizontal)mean curvature H=2nλ(see Section 2 in[8]for instance).
In[9],we study umbilic hypersurfaces of constant general sigma-i curvature σi,n.We have the following result.
Theorem 3.1. Let Σ be an immersed,connected,orientable,closed,umbilic hypersurface of Hn,n≥2 with nonvanishing Euler number.For a given i,1≤i≤2n−1,suppose σi,nof Σ is a positive constant. Then Σ must be a Pansu sphere up to a Heisenberg translation.
Theorem 3.2. Let Σ be an immersed, connected, umbilic hypersurface in Hn, n ≥2. Let SΣdenote the set of all singular points in Σ.Then
(a)either α2+k2≡0 on Σ or α2+k2>0 at all points in ΣSΣ.
(b) Suppose α2+k2≡0 on Σ. Then Σ is congruent to part of a hypersurface Cn−1×γ×R where γ is a curve in the Euclidean plane C with signed curvature l(=H).
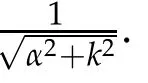
For the situation of σi,n=c ≤0,we have the following result.
Theorem 3.3. Let Σ be an immersed,connected,umbilic hypersurface of Hn,n ≥2.
(a)Suppose σi,n=c=0.Then there is no closed such hypersurface Σ.
(b)Suppose σi,n=c<0.Then for i odd,1≤i≤2n−1,any closed such hypersurface Σ must be a Pansu sphere up to a Heisenberg translation.
We remark that for the case σi,n=c<0,i ≥4 and even,there may correspond closed umbilic hypersurfaces which are not congruent to Pansu spheres (see Figure 4.2 and Proposition 4.2 in[9]).
4 Strong maximum principle for mean curvature operators
In this section,we describe the results in the paper[10]. E.Hopf probably was the first to study the strong maximum principle(SMP in short)of elliptic operators in its generality.This principle has been extended to certain quasilinear elliptic operators of second order.In 1969, J.-M. Bony studied, among others, the SMP for linear operators of H¨ormander type including some known subelliptic operators.Bony’s SMP has been applied to study various geometric problems. See, for instance, B. Andrews’ work on noncollapsing in mean-convex mean curvature flow or S.Brendle’s solution to the Lawson conjecture.
In[10],we first extend Bony’s SMP to the quasilinear case and then apply it to(generalized)mean curvature equations in subriemannian geometry,including p-sublaplacian and usual horizontal(p-)mean curvature. We consider quasilinear equations Q of second order:
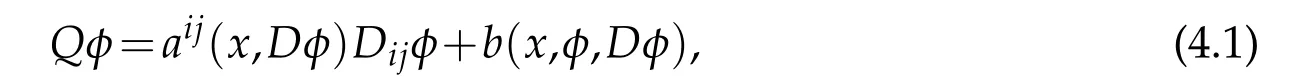
where x=(x1,···,xm+1)is contained in a domain Ω of Rm+1,m≥1. The coefficients aij(x,p)(b(x,z,p), resp.) of Q are assumed to be defined and C∞smooth (for simplicity) for all values of(x,p)((x,z,p),resp.) in the set Ω×Rm+1(Ω×R×Rm+1,resp.). Let£(X1,···,Xr)denote the smallest C∞-module which contains C∞vector fields X1,···, Xron Ω and is closed under the Lie bracket.The following comparison principle is a straightforward application of Bony’s SMP and an idea in the proof for Theorem 10.1 in the book of Gilbarg and Trudinger.
Theorem 4.1. Let φ,ψ ∈C∞(Ω)satisfy Qφ≥Qψ in Ω.Assume
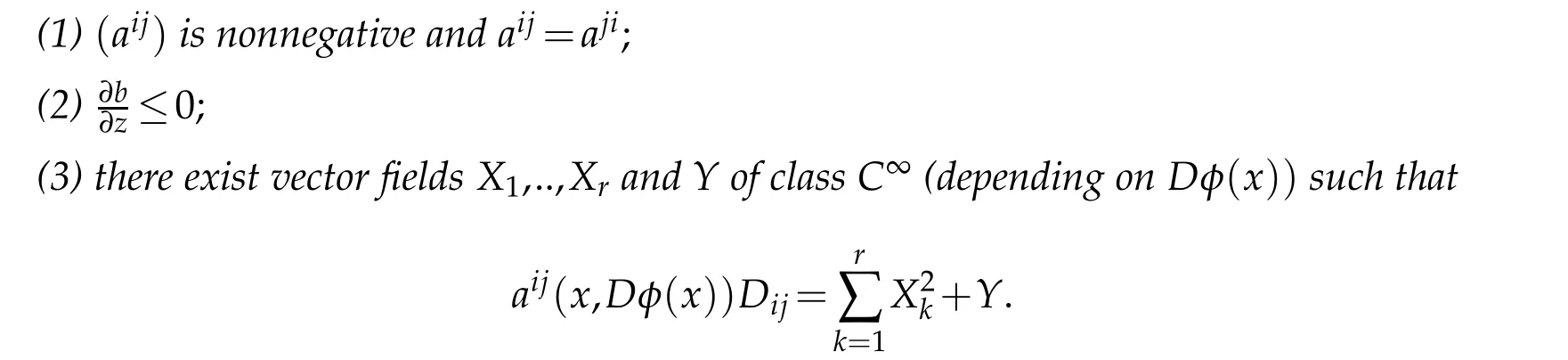
Let Γ be an integral curve of a vector field Z ∈£(X1,...,Xr). Suppose φ−ψ achieves a nonnegative maximum in Ω at a point of Γ,then the maximum is attained at all points of Γ.
We also give the moving frame version of Theorem 4.1 and condition (3) can be replaced by the constant rank condition.
In applications,we usually assume φ ≤ψ and φ=ψ at a point p0. Then we conclude φ ≡ψ on a hypersurface Σ containing p0if the Lie span £(X1,...,Xr) = C∞(Σ,TΣ). We are going to apply a variant of Theorem 4.1 to generalized mean curvature equation or p-laplacian Hφ,pwith p≥0.

For p=0,Hφ,0,often denoted as Hφ,is called(Riemannian,subriemannian,or horizontal)mean curvature while,for p>0, Hφ,pis so called p-laplacian or p-sublaplacian. We have a variational description for Hφ,p.
In[10],we mainly deal with the SMP near nonsingular points(where|dφ|∗/=0,|dψ|∗/= 0).For the SMP near singular points,we only discuss the situation that the reference singular point is isolated for at least one comparison hypersurface. In general,the problem of the SMP near singular points is still open.
Let φ and ψ be defining functions for hypersurfaces Σ1and Σ2in a subriemannian manifold(M,<·,·>∗)of dimension m+1,resp. (m≥1). Namely,Σ1(Σ2,resp.)is defined by φ=0(ψ=0,resp.). Suppose Σ1and Σ2are tangent to each other at a point p0where|dφ|∗/=0,|dψ|∗/=0.Define G:T∗M →TM by ω(G(η))=<ω,η>∗for ω,η ∈T∗M.Let ξ := Range(G).Throughout[10],we assume
near p0with l being a nonnegative integer unless stated otherwise. We call l the degree of degeneracy of M.Note that dimkerG=l.The following rank condition:

for any local sections X1,···,Xm−lof ξ, which are independent wherever defined,is important.It means that any(m−l)-dimensional subspace of local sections of ξ can generate m-dimensional spaces. Let
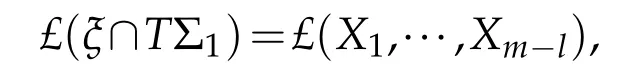
where X1,···,Xm−lform a basis of local sections of ξ∩TΣ1near p0.Similarly we can define
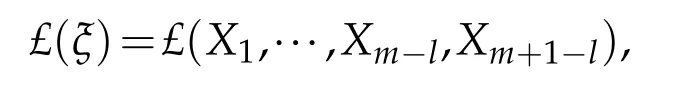
where X1,···,Xm−l,Xm+1−lform a basis of local sections of ξ near p0.Note that both£(ξ∩TΣ1)and£(ξ)are independent of choice of a basis of local sections.Then,using a variant of Theorem 4.1,we have
Theorem 4.2. Suppose we are in the situation described above,in particular,|dφ|∗/=0,|dψ|∗/=0 at p0.For p≥0,Assume

We say the defining function φ of a(local)hypersurface Σ passing through p0is compatible with{Ψa}or{Ψa}is compatible with the defining function φ if
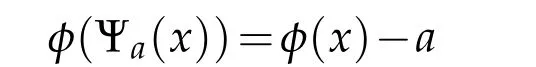
for x ∈Σ ∩U (and hence x ∈U) and a ∈(−δ,δ). {Ψa} is said to be transversal to a hypersurface Σ of U if

for all x ∈Σ.
We will show the existence of some special coordinates for a subriemannian manifold having local isometric translations as shown below.
Theorem 4.3. Let(M,<·,·>∗,dvM)be an(m+1)-dimensional subriemannian manifold with a background volume form dvM.Suppose(M,<·,·>∗,dvM)has isometric translations Ψa,a ∈(−δ,δ)for δ>0,near p0∈M,transversal to a hypersurface Σ passing through p0.Then we can find local coordinates x1,x2,···,xm+1in a neighborhood V of p0such that
(1) Σ is described by xm+1= 0 in V, p0is the origin, xj◦Ψa= xjat q ∈V for any a such that Ψa(q)∈V,1≤j≤m,and xm+1◦Ψa= xm+1+a;
(2) A(Ψa(q)) = A(q)for any q ∈V and any a such that Ψa(q)∈V if we write dvM(q)=A(q)dx1∧···∧dxm+1.
Call this system of special coordinates above in Theorem 4.3(a system of)translationisometric coordinates.
Definition 4.2. Take a system of translation-isometric coordinates x1,x2,···,xm+1as in Theorem ˆC.A Ψagraph is a graph described by
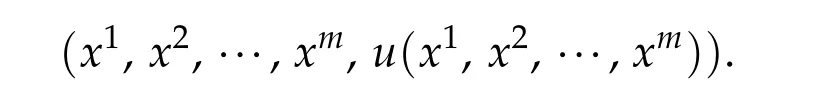
For a Ψagraph, we take the defining function φ = u(x1, x2,···,xm) −xm+1which is compatible with{Ψa}.For p ≥0,we define
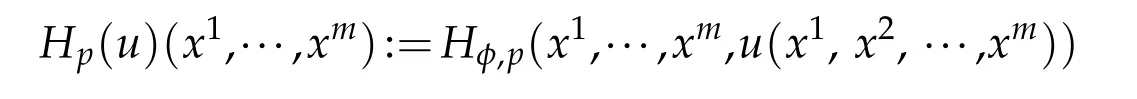
at(x1,..,xm) where |dφ|∗/= 0. Making use of translation-isometric coordinates, we have Theorem 4.4′,which is an application of Theorem 4.2.
Theorem 4.4. Suppose (M, <·,·>∗,dvM) of dimension m+1 has isometric translations Ψanear p0∈M,transversal to a hypersurface Σ passing through p0.Take a system of translationisometric coordinates x1, x2, ···, xm+1in a neighborhood V of p0such that xm+1= 0 on Σ.Suppose u(v,resp.) :Σ∩V →R defines a graph{(x1, x2,···xm,u(x1, x2,···,xm))}({(x1, x2,···,xm,v(x1,x2,···,xm))},resp.) ⊂V such that|d(u−xm+1)|∗/=0(|d(v−xm+1)|∗/=0,resp.).Assume
(1)v≥u on Σ∩V and v(0,···,0)=u(0,···,0)=0;
(2)For some p≥0, Hp(v)≤Hp(u)on Σ∩V.
Moreover, assume that the rank condition (4.2)holds near p0.Then v ≡u in a neighborhood of p0∈Σ.

Applying our theory of translation-isometric coordinates to the situations of lagraphs,as well as intrinsic graphs, we respectively obtain the corresponding SMP. Notice that we have a more geometric description for this theory. We remark that the horizontal mean curvature operator of an intrinsic graph u does not belong to the type (4.1) since the second order coefficients contain u itself. So Theorem E in[10] does not follow directly from the previous general theorems.
We can proceed with the application of Theorem 4.4 as follows. Let Ω be a(connected and open)domain of Rm.Let u,v be two C∞smooth,real valued functions on Ω.Let →F be a C∞smooth vector field on Ω.We remark that for some situations it is sufficient to have only finite differentiability, but for simplicity we work in C∞category (unless specified otherwise). Define the Legendrian(or horizontal)normal(u)(resp.(v))of u(resp.v)by

We show that the rank condition in Theorem 4.5 can be replaced by some easy to check conditions,which are formulated as Corollary G and Corollary H in[10]. Corollary I of[10]is just the special situation of Theorem 4.5 for the standard Heisenberg groups.
Finally, for the SMP near singular points, we turn to discuss the situation that the reference singular point is isolated.

Theorem 4.7. Let Σ1and Σ2be two connected, orientable, closed hypersurfaces of constant horizontal(p-)mean curvature HΣ1and HΣ2,resp. in Hn,n ≥2.Suppose Σ2is inscribed in Σ1,i.e., Σ2is contained in the closure of the inside of Σ1and Σ1∩Σ2is not empty. Assume HΣ2≤HΣ1and Σ1∩Σ2contains a nonsingular (with respect to both Σ1and Σ2) point or an isolated singular point of Σ1(Σ2, resp.). Moreover, assume either Σ1or Σ2has only isolated singular points. Then Σ1≡Σ2.
For further applications we need to extend Theorem 4.6 to hypersurfaces of a subriemannian manifold having isometric translations, touching at an isolated singular point.See Theorem J′in[10].
We can now apply Theorem C(or Theorem 4.4 above)and Theorem J′in[10]to prove a rigidity result for minimal hypersurfaces in a Heisenberg cylinder(Hn{0},ρ−2Θ)with n ≥2.Here Θ denotes the standard Heisenberg contact form:
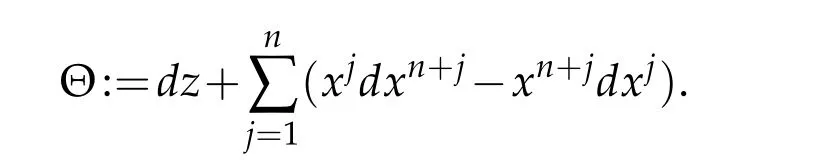
The associated Heisenberg distance function ρ reads
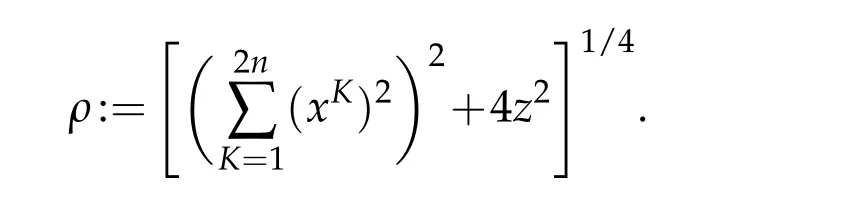
We discuss some basic geometry associated to the contact form ρ−2Θ(using xj,yjinstead of xj,xn+jand both interchangeably)before proving the following result.
Theorem 4.8. Let Σ be a closed(compact with no boundary)immersed hypersurface in a Heisenberg cylinder(Hn{0},ρ−2Θ)with n ≥2.Suppose either
(a) HΣ≤0 or
(b)HΣ≥0 and the interior region of Σ contains the origin of Hn.
Then Σ must be a Heisenberg sphere defined by ρ4=c for some constant c>0.In particular, HΣ≡0.
Corollary 4.1. There does not exist a closed immersed hypersurface of positive constant horizontal(p-)mean curvature in a Heisenberg cylinder(Hn{0},ρ−2Θ)with n≥2,whose interior region contains the origin.
Let ϕ be a continuous function of τ ∈[0,∞). We have the following nonexistence result(pseudo-halfspace theorem).
Theorem 4.9. Let Ω be a domain of Hn,n ≥2,defined by either
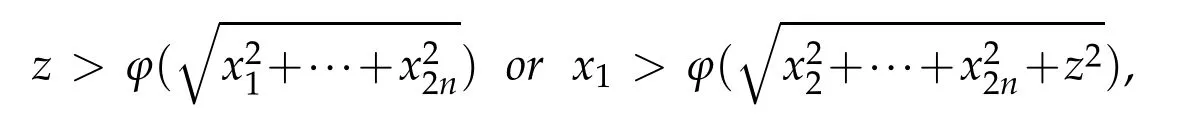
where limτ→∞ϕ(τ) = ∞. Then there does not exist any horizontal (p-) minimal hypersurface properly immersed in Ω.
The simplest example for Theorem 4.9 is ϕ(τ) = aτ with a > 0. Call the associated domains wedge-shaped. Theorem 4.9 tells us nonexistence of horizontal (p-) minimal hypersurfaces in wedge-shaped domains. But Theorem 4.9 does not hold for the case a= 0. That is, halfspace theorem does not hold since there are catenoid type horizontal(p-)minimal hypersurfaces with finite height in Hnfor n ≥2.On the other hand, we do have halfspace theorem for H1([11]). Hoffman and Meeks first proved such a halfspace theorem for R3.It fails for Rnwith n≥4.But the above type of pseudo-halfspace theorem still holds for Rnwith n≥4 by a similar reasoning.
There is another notion of mean curvature,called Levi-mean curvature,in the study of real hypersurfaces in Cn.We would like to remark that the SMP for such mean curvature operators(generalized to pseudoconvex fully nonlinear Levi-type curvature operators)has been proved by Montanari and Lanconelli. On the other hand,there are other assumptions under which the SMP holds and examples which are not of the type: sum of squares and may have degeneracy of arbitrary order.
5 Chains in CR geometry
In this section we would like to introduce results in[14]about chains in CR geometry as geodesics of a Kropina metric. A CR structure on a 2n+1 dimensional manifold M is a pair(ξ,J) where ξ is a contact distribution and J is a complex structure on ξ satisfying a certain integrability condition.
The chains for a CR geometry are a family of curves on M which are canonically constructed from the CR structure (for one of several equivalent definitions of chains, see the comments in the next paragraph). See,for instance,the book[24]and the references therein. For any point of M and any direction not contained in ξ there exists precisely one chain through this point and tangent to this direction.
One of several equivalent definitions of chains goes through the Fefferman metric introduced in[19],which is an indefinite metric on a circle bundle over M.The conformal class of the Fefferman metric is canonically constructed from the CR structure on M. The infinitesimal generator K of the circle action is a null Killing vector field for this metric.Chains are then defined to be the projections to M of null geodesics for this pseudo-Riemannian metric to M.
On the other hand,the Kropina metric is a function on TM given by

where g is a metric and ω is a nonvanishing 1-form on M. In [14] we allow metrics g of all signatures;in fact,we will also allow certain degenerate metrics: as it will become clear below,in order to define geodesics it is sufficient that the restriction of g to kerω is non-degenerate.
Kropina metrics are popular objects in Finsler geometry, despite the fact that they are not strictly speaking Finsler metrics even when g is positive definite. Indeed F is undefined for η ∈kerω.
Our first result is the following theorem.
Theorem 5.1. Chains are geodesics of a certain Kropina metric.
By a geodesic of a Kropina metric F=g/ω we mean any smooth regular solution γ(t)of the Euler-Lagrange equation for the Lagrangian F satisfying the additional property that F(γ(t),γ′(t))is defined(i.e.,ω(γ′(t))/=0)for all t.
In Section 4.3 of [14], we give a formula for this Kropina metric. When M is the boundary of a strictly pseudoconvex domain and ρ is Fefferman’s defining function for M then we can express this metric as F=(∂∂ρ)/Im(∂ρ)where we regard ∂∂ρ as a symmetric 2-tensor restricted to M and Im(∂ρ)as a one-form restricted to M.
In Theorem 5.1, we consider geodesics without preferred parameterization. Clearly,F(x,η)=−F(x,−η),so that for a geodesic γ(t)the curve γ(C−t)for an appropriate constant C is also a geodesic.For any point(x,η)∈TM such that ω(η)/=0,there exists a local geodesic of g/ω,unique up to re-pameterization,which starts at x tangent to η.
To formulate the next result and apply it to CR geometry,we only need to know that F has the form g/θ,where θ is a contact form for the underlying contact structure on the CR manifold M.The metric g is defined up to the transformation gg+θ·β with a closed 1-form β. Clearly this transformation corresponds to an addition of the closed form β to the Kropina metric,and does not change its geodesics.
The Kropina metric also has a relation to a different topic in CR geometry.We consider the energy functional E(γ),the integral of the Kropina metric over a curve γ transversal to the contact distribution in the CR manifold M. Suppose M bounds an asymptotic complex hyperbolic domain Ω and γ bounds a minimal surface Σ in Ω. In[30],E(γ)was shown to appear as the log term coefficient in the area renormalization expansion of Σ for dimM=3.
The next result concerns the projective equivalence of Kropina metrics. According to the classical definition, two geometric structures(Riemannian, Finsler,or affine connections)are projectively equivalent if they have the same geodesics. In the case of Kropina metrics,we will modify this definition. The reason for this modification is that Kropina geodesics are not defined precisely along directions lying in the kernel of ω. Thus if two Kropina metrics are projectively equivalent according to the classical definition,then their 1-forms coincide up to scale, which is an extremely strong additional condition.Note that Theorem 5.3 below shows that for certain Kropina metrics we can not reconstruct the kernel of ω by the geodesic equation.
We call a set of curves on the manifold M sufficiently big if for any point p∈M the set of tangent vectors at p for these curves contains a nonempty open subset of TpM. We call two Kropina metrics projectively equivalent, if there exists a sufficiently big set of curves which are geodesics for both metrics.
Our second result is the following theorem:

Note that[6]assumes that all chains of one structure are chains of the other structure.As explained above, this implies that the corresponding 1-forms are proportional. The latter assumption essentially simplifies the proof. Similarly, [3] requires that the corresponding contact distributions coincide.
Theorem 5.2 describes all pairs of projectively equivalent Kropina metrics such that for at least one of them the kernel distribution of the corresponding 1-form is non-integrable. Let us now consider the remaining case, i.e., when for both 1-forms the kernel distributions are integrable. In this case without loss of generality we can assume that the 1-forms are certain affine connection.
Theorem 5.3. If the 1-form ω is closed, then for any Kropina metric F=g/ω there exists an affine connection ∇=(Γijk)such that each geodesic of F is a geodesic of ∇.
The precise formula for the connection is in Theorem 3.9 of[14]. It is torsion-free.
In particular, in dimension 2, all Kropina metrics are projectively closed. The next theorem shows that then the geodesics are geodesics of a equivalent to affine connections.This is actually known and was one of the motivations for introducing Kropina metrics,see[27]. Note that the question when two affine connections are projectively equivalent is well understood,see e.g.[28].
Chern and Moser[18,p.222]suggested to us to think of chains as the CR versions of geodesics.If their analogy is a good one,then any two sufficiently nearby points ought to be connected by a chain,and if M were compact and connected,then any two points at all ought to be connected by a chain. The first assertion does hold for strictly pseudoconvex CR manifolds: nearby points are connected by chains. See [24], p.185, and the original references therein,including[25,26]. Surprisingly,the second assertion is false,even if the compact manifold is locally CR equivalent to the standard model, S3with its canonical strictly pseudoconvex structure. This example, the Burns-Shnider counterexample, is detailed in[24,p.185]. See also the original reference[2].
The fact that chains are geodesics of a Kropina metric allows us to employ variational methods and techniques of metric geometry to investigate them.We will use these methods to reprove and generalize the famous result of[25,26]on local chain connectivity.
Theorem 5.4. Let F=g/ω be a Kropina metric on M with g positive definite. Then,the following statements hold:
(A)If at p∈M we have ω∧dω/=0,then there exists a neighborhood U of p such that for any q∈U one can join p to q by a length minimizing Kropina geodesic which does not leave U. This neighborhood U can be chosen to be arbitrary small.
(B)Suppose that M is compact and assume that the set of the points p∈M such that ω∧dω/=0 is connected and everywhere dense in M. Then, any two points of M can be joined by a lengthminimizing Kropina geodesic γ such that F(γ(t),γ′(t))>0 at each point.
We will see that for strictly pseudoconvex CR manifolds the corresponding metric g can be made positive definite locally. This follows from Lemma 3.1 of [14] applied to the Kropina metric associated to a strictly pseudoconvex CR manifolds. Moreover,on a strictly pseudoconvex CR manifold admitting a pseudo-Einstein contact form with positive Tanaka-Webster scalar curvature,the metric g can be made positive definite globally(see (4.6) in [14]). On strictly pseudoconvex CR manifolds we have by definition that ω∧dω/=0 at all points. Therefore,we obtain:
Corollary 5.2. Let M be a strictly pseudoconvex CR manifold. Then the following statements hold:
(A)Each point p∈M has a neighborhood U such that any q∈U is connected to p by a chain lying in U.
(B)If M is connected,compact and admits a pseudo-Einstein contact form with positive Tanaka-Webster scalar curvature,then,any two points of M can be joined by a chain.
The Burns-Shnider example mentioned above is a CR structure on a compact manifold S2n×S1such that not every two points can be connected by a chain. It follows from Corollary 5.2 that we cannot find a pseudo-Einstein contact form with positive Tanaka-Webster scalar curvature for this CR structure.
6 Invariant surfaces in a CR 3-manifold
Motivated by the recent study [21] of the singular Yamabe problem and the associated volume renormalization in conformal geometry,we looked into the analogous situation in CR geometry for the case of dimension 3[16]. Let us make a brief review of what has been done in[16].
For a CR analogue of the Willmore energy in the surface case,two CR invariant surface area elements dA1, dA2were found in 1995 (see [7]). Since there have been well developed local invariants for surfaces in a CR 3-manifold (see, for instance, [12, 13]and[8]),we can easily express dA1,dA2in terms of quantities in pseudohermitian geometry.
To be more precise, let us review some basic notions for a nonsingular surface Σ in a pseudohermitian 3-manifold (M,J,θ). We refer the reader to [12] for more details. On(M,J,θ),there is a canonical connection ∇,called Tanaka-Webster connection or pseudohermitian connection. Associated to this connection, we have the torsion A11, Tanaka-Webster (scalar) curvature W. Associated to the contact form θ, we have the so called Reeb vector field T.Associated to Σ,we have a special frame e1,e2:= Je1such that e1∈TΣ ∩kerθ and has unit length with respect to the Levi metric12dθ(·,J·). We denote the coframe dual to e1,e2and T as e1,e2and θ.A deviation function α on Σ is defined so that T+αe2∈TΣ.We define mean curvature H of Σ in this geometry,called p-mean curvature or horizontal mean curvature,so that ∇e1e1= He2.
In Theorem 1 of Section 2 in[16],we obtain

We then have two energy functionals defined by

The Euler-Lagrange equation for E1was derived in[7]in terms of quantities in Cartan’s theory of 3-dimensional CR geometry.In Section 3 of[16],we express relevant quantities in terms of pseudohermitian geometry.The Euler-Lagrange equation for E1reads So they are minimizers for E1with zero energy.Conjecture 6.1. The shifted Heisenberg spheres are the only closed minimizers for E1(with zero energy)in H1.


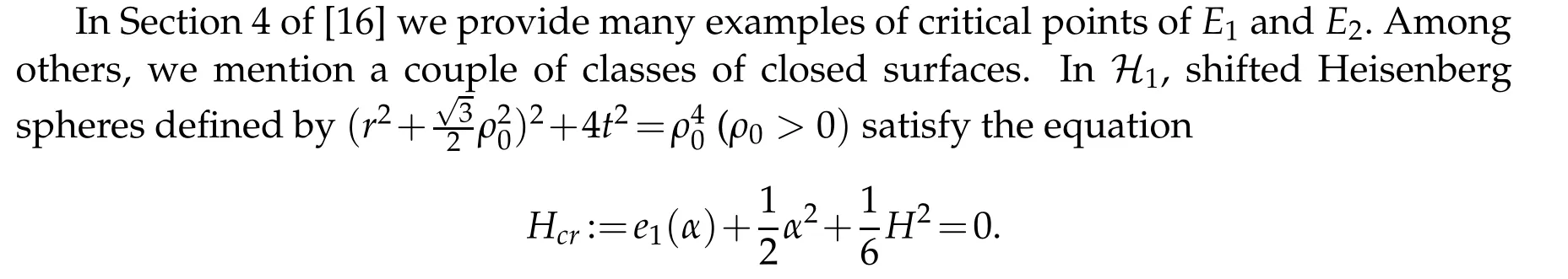
7 Singular Yamabe problem and complex/minimal submanifold asymptotics
In Section 5 of[16],we study the expansion of a formal solution to the singular CR Yamabe problem. Let(M,J,θ)be a 3-dimensional pseudohermitian manifold with boundary Σ= ∂M. Consider the conformal change of θ : ˜θ =u−2θ.The singular CR Yamabe problem is to find u such that

where x is a regular(or nonsingular)point of Σ and ρ is a suitably chosen defining function for Σ. We can determine c(x) ≡1 easily. In Section 5 of [16], we give explicit expressions (5.10), (5.14) and (5.23) for v(x), w(x) and z(x), resp.. The coefficient l(x) of the first log term is related to E2and discussed in Section 6 of [16] about the volume renormalization.
We consider the volume renormalization for a formal solution to(7.1)as follows:
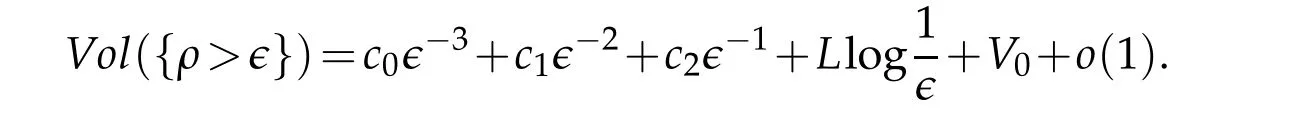
We deduce explicit formulas for the coefficients c0,c1,c2and L.See(6.7)in[16]. We show that

for Σ being a closed,nonsingular surface. Finally,we prove that
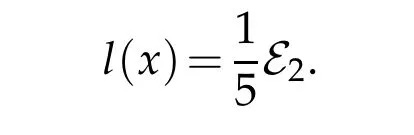
This is the CR analogue of the result for the singular Yamabe problem[20], [21]. In particular, E2/=0 is also an obstruction to the smoothness of solutions to the singular CR Yamabe problem.
We would like to extend the above result to the higher dimensional situation. For the existence of the solution(including every dimension),we want to solve the singular CR Yamabe problem, which is a complex version of the work of Andersson,Chrusciel and Friedrich[1].
In the conformal case,the Willmore energy(including dimensions higher than two)of a(hyper)surface in the boundary of a hyperbolic space can be recovered as the log term coefficient in the volume renormalization expansion for minimal submanifold asymptotics in the hyperbolic space(see[22]). But in the CR case,minimal submanifold asymptotics in the complex hyperbolic space do not have the log term in the renormalized volume expansion with respect to the standard complex hyperbolic metric. On the other hand, there might be a weighted volume with respect to which the expansion contains the log term in view of Hirachi’s weighted volume for the whole space[23].
Let us explain Hirachi’s weighted volume as follows. Let D⊂Cn+1be a strictly pseudoconvex domain with C∞boundary M=∂D. Then by[17]D admits a defining function r (positive in D and dr/=0 on ∂D) such that −i∂logr (K¨ahler form of a metric g) is Einstein-K¨ahler with negative scalar curvature(which we normalized to be −n−2). On the other hand,the total Q-prime curvature
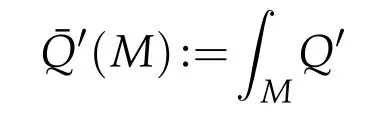
is a CR invariant of M[4]. By analogy with the fact,that the total Q-curvature in conformal geometry is given by the logarithmic term in the asymptotic expansion of the volume of conformally compact Einstein manifold, one may hope that(M) is a coefficient of the asymptotic volume expansion of D.It is indeed the case,but is not with respect to the volume form dvgof g.(M)appears in the expansion with respect to the volume form weighted by||dlogr||2,the squared norm of the 1-form dlogr for g:
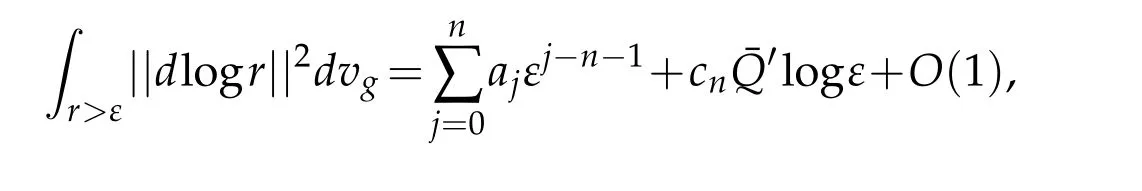
where cn=(−1)n/(n!)3.So for minimal submanifold asymptotics in D,we hope to find a similar weighted volume such that the volume renormalization expansion has a log term and its coefficient recovers the E1energy for a surface lying in M=∂D for the n=1 case.
For complex submanifold asymptotics,their boundary manifolds have codimension higher than 1 in ∂D. In such a situation,we have two interesting cases to look into. The first case is the dimension 1 situation. Namely suppose a closed curve γ in the boundary∂Ω of a bounded strongly pseudoconvex domain Ω ⊂C2bounds a holomorphic disc(resp. a minimal surface in general) D in Ω. We expect the log term coefficient of the asymptotic weighted volume expansion of D near γ should give a CR invariant energy of γ. The vanishing of its variational derivative should describe γ as a chain of Cartan and Moser(see Chapter 8 in[24]). Indeed this is true as shown in[30].
On the other hand,a closed curve in a space of 3D can be knotted.We ask if it is possible to have a knotted chain. If such a situation happens,can we express knot invariants of a chain in terms of quantities in gauged complex/CR geometry in view of the recent study of the Kapustin-Witten equations([29])?
The other case is the dimension 3 situation. Namely suppose a 3 dimensional submanifold Σ in ∂Ω (dimension 5) of a bounded strongly pseudoconvex domain Ω ⊂C3bounds a complex surface N in Ω.It follows that Σ=∂N must be a CR submanifold of ∂Ω(with codimension 2). We expect the log term coefficient of the renormalized weighted volume expansion of N to be a CR invariant energy functional for Σ in ∂Ω.So this gives us motivation to find out CR invariant volume elements for a submanifold lying in a CR manifold with higher codimension.
Acknowledgement
The author is supported by the Ministry of Science and Technology of Taiwan Grant No.108-2115-M-001-010.
