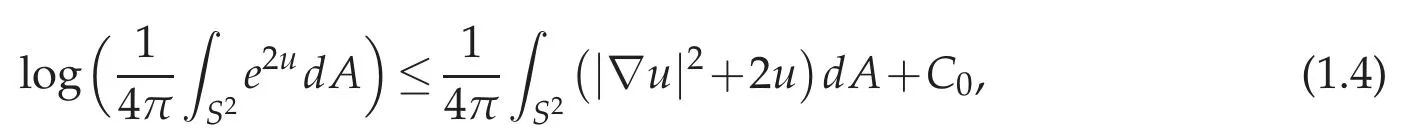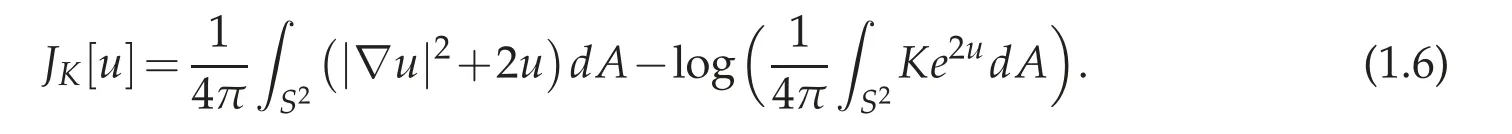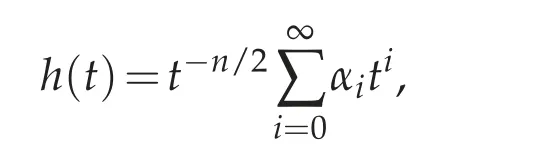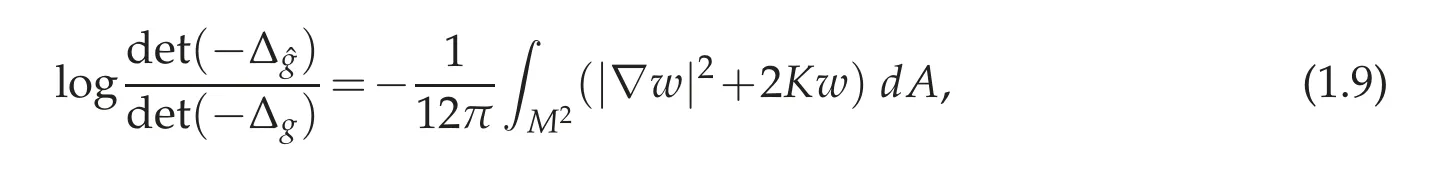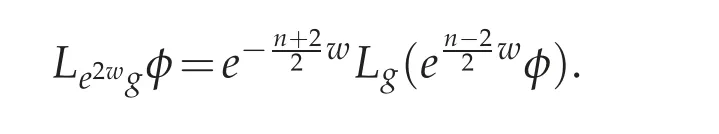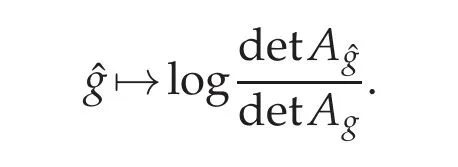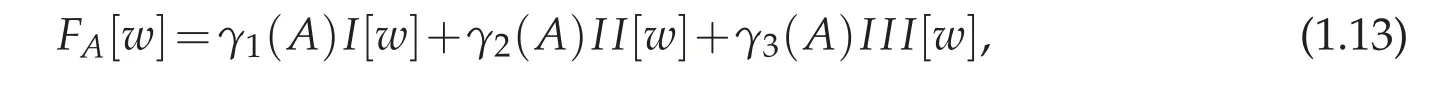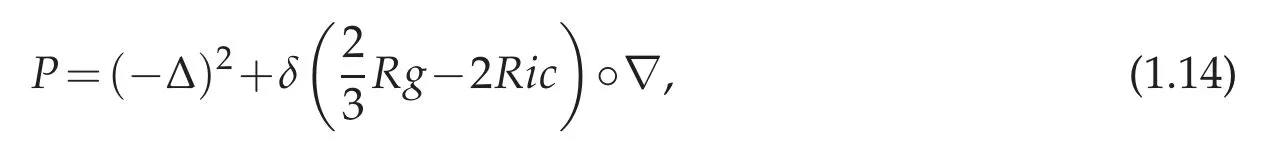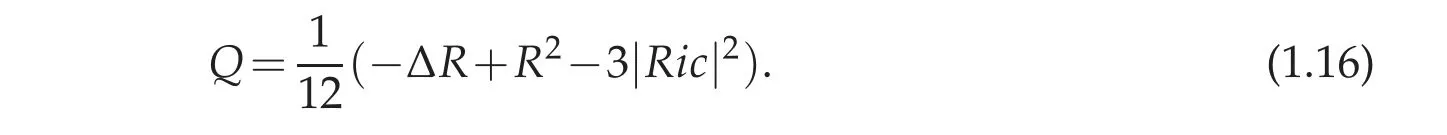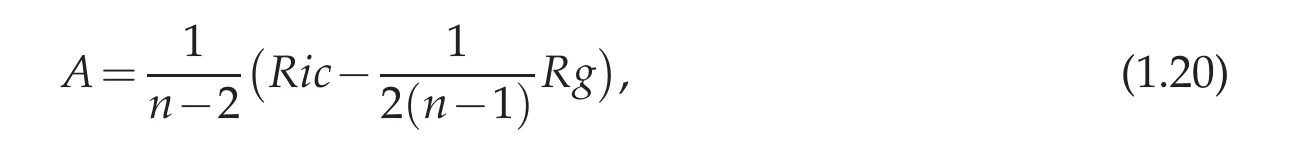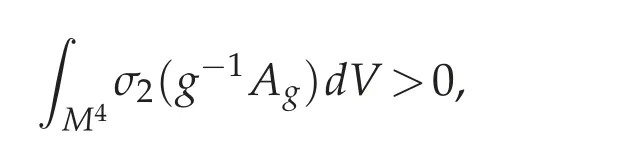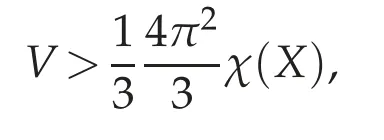The Mathematical Work of S.-Y.Alice Chang and Paul C.Yang

Matthew J.Gursky

Department of Mathematics,University of Notre Dame,Notre Dame,IN 46556.

Received December 5,2020;Accepted December 12,2020;

Published online December 21,2020.

1 Introduction

Writing an article about the mathematical work of Alice Chang and Paul Yang is simultaneously a great honor and an almost hopeless task.How does one begin to summarize the work of two accomplished mathematicians, whose combined careers span almost a century? First, there is the sheer volume of output: since receiving their PhDs in the early 1970s, Paul and Alice have each published over 100 articles (about half on which they were co-authors). Then there is the diversity of fields: complex geometry, nonlinear PDEs, spectral geometry, calculus of variations, conformal geometry, CR geometry,functional inequalities, etc. And finally, there are the many students and postdocs Paul and Alice have mentored over the years(the author of this article included). Consequently, even a cursory overview could easily fill several issues of the Journal of Mathematical Study.

However, I also know that Paul and Alice would vastly prefer reading research articles about topics that interest them, rather than a lengthy paean in their honor. I will therefore turn necessity into a virtue,and attempt to distill two rich mathematical careers into a few pages. There will necessarily be gaps;some research topics I will barely touch,while for others I will try to give enough context in order to better appreciate their contributions. It also behooves me to point out that this is a provisional survey, since Paul and Alice remain very active!

I will proceed chronologically rather than topically, and since Paul is more senior,I will begin with him. Paul (Chien-Ping) Yang was born in 1947, in Changhua, Taiwan.His family immigrated to the United States in 1962,and settled in San Francisco. Paul did his undergraduate and graduate work at UC Berkeley,receiving his PhD in 1973 under the direction of Hung-Hsi Wu. From 1974-1976 he was an Evans Instructor at Rice, the first stop on a peripatetic early career that brought him to Maryland, Stanford and IUBloomington before arriving at the University of Southern California in 1982. He was at USC almost 20 years,until 2001 when he joined the faculty at Princeton.

Paul’s early work was in complex geometry. His first paper[53], which appeared in Duke Math. J.,studied complete K¨ahler metrics with non-positive holomorphic bisectional curvature, a problem that would occupy his interest for some time. In a subsequent Inventiones paper co-authored with Y. T. Siu [51], “Compact K¨ahler-Einstein surfaces of nonpositive bisectional curvature”,they conjectured that every compact K¨ahler-Einstein surface with negative sectional curvature is biholomorphic to a compact quotient of the complex 2-ball. They were able to prove the conjecture assuming a kind of pinching condition on the holomorphic sectional curvatures (which, interestingly, permits nonpositive holomorphic bisectional curvature,as opposed to strictly negative).

One of Paul’s other papers from this period prefigured some of his later research interests.In“Local boundary regularity of holomorphic mappings”(Comm.Pure Appl. Math),joint with S.Webster and L.Nirenberg[48], they gave a simplified proof of Fefferman’s result that a biholomorphic map of strictly pseudoconvex domains extends smoothly to the boundaries. Relating the (real) geometry of the boundary of a complex domain to function theory in the domain is one of the origins of CR geometry,a field to which Paul would make beautiful contributions later in his career (as we will see below). On the basis of his work during this period Paul was awarded a Sloan Fellowship in 1981.

Sun-Yung Alice Chang was born in Xi’an, China, in 1948, and grew up in Taiwan.After completing her undergraduate work at National Taiwan University, she came to the US in 1970 at attend UC Berkeley for graduate school. It was during their time at Berkeley that Paul and Alice met,and were married in 1973. Alice received her PhD in 1974 under the direction of Donald Sarason. After Berkeley,Alice had positions at SUNYBuffalo(1974-75),UCLA(1975-77),and Maryland(1978-1980),before returning to UCLA.She was on the faculty of UCLA from 1980 to 1998.

Early in her career,Alice worked in the field of classical harmonic analysis,operator theory,and algebras of functions of one complex variable. One of her earliest accomplishments was her work on the Douglas Problem,which was introduced to her by Sarason,who did pioneering work on the conjecture. Alice’s Acta paper, “A characterization of Douglas subalgebras” [9]), when combined with the results of Donald Marshall, completely resolved the conjecture. Over the next decade she continued making important contributions to the field,including two papers that appeared in the Annals of Mathematics:“Carleson measure on the bi-disc”[10]and“On a continuous version of duality of H1with BMO on the bi-disc” [11]), joint with R. Fefferman. In the latter paper, Chang and Fefferman studied the question of extending H1-BMO duality to functions on the polydisc.In particular,they have a much simpler and more natrual description of the dual of H1than any appearing in the literature at that time. Alice’s work over this period was recognized with an Alfred P.Sloan Fellowship in 1979-1980.

It was Alice’s paper with L. Carleson(”On the existence of an extremal function for an inequality of J.Moser”[6])that was a bridge from her background in classical analysis to her subsequent work in geometric analysis. It remains her most highly cited paper.

It is well known that if Ω ⊂Rnis a bounded domain and 1

Subsequently,Moser found the sharp value of β(n).

The idea of Trudinger’s original proof of (1.2) (which did not capture the best constant)was to expand the Taylor series of eβ|u|nn−1and use the classical Sobolev inequality(1.1). In this sense,(1.2)can be thought of as a consequence of(1.1). It was therefore quite surprising when Carleson-Chang showed that when Ω is the unit ball, then an extremal function for(1.2)does exist.

There is also a version of the inequality(1.2)for functions defined on the unit sphere S2. Let(S2,g0)denote the unit sphere with its standard Riemannian metric;then

where dA is the area form with respect to g0anddenotes the mean value of u. This implies another inequality,sometimes referred to as its‘linearized’version:

for some constant C0that is independent of u.

The sharp form of(1.2)and its counterpart on the sphere were proved by Moser[44].His motivation was,in part,its importance when studying the Nirenberg problem: Given K ∈C∞(S2), is there a conformal metric g=e2ug0such that the Gauss curvature of g is given by K? A standard calculation shows that this question can be answered in the affirmative if and only if one can find a solution of the PDE

where ∆0is the Laplace-Beltrami operator with respect to g0. This equation is variational:let J:H1,2(S2)→R be given by

It is not difficult to see that u is a critical points of J if and only if it is a(weak)solution of(1.5).

Not long after the work with Carleson,Paul and Alice began a long and very fruitful collaboration. Their first joint paper, “Prescribing Gaussian curvature on S2” was on the Nirenberg problem, and appeared in Acta Math in 1987 [28]. For a positive function K∈C∞(S2),they gave two different necessary conditions for the existence of a conformal metric g with Gauss curvature K. The statements are somewhat technical,so we will only give one of them:

Theorem 1.1(Theorem II of[28]). Let K be a positive smooth function with only non-degenerate critical points, and in addition assume ∆0K(p)/=0, where p is any critical point. Suppose there are at least two local maximum points of K,and at all saddle points q of K,K(q)>0. Then K is the Gauss curvature of some metric conformal to g0.

where by convention the eigenvalues are counted with their multiplicities. Two Riemannian metrics are isospectral if their respective laplace operators have the same spectrum.One theme of spectral geometry is the extent to which the spectrum of a Riemannian manifold determines the metric. For example,are two isospectral metrics isometric? Milnor showed that this is not the case, but one can still ask to what extent the spectrum influences the geometry,and vice versa. For example,is the set of isospectral metrics on a fixed manifold M compact? One way to approach these kinds of questions is to study geometric invariants that are built up from the spectrum,e.g.,the trace of the heat kernel h(t).

By a result of Minakshisundaram-Pleijel [43], if h(t)=∑je−tλjis the L2-trace of the heat kernel,then h has an expansion

where n=dimM. Moreover, each αiis given by the integral of a local invariant of the metric. For example,the first few coefficients are given by

where Rgis the scalar curvature and Ricgis the Ricci tensor of g, and the coefficients c2,n,c′2,n>0.

Isospectral metrics have the same heat coefficients,hence(by the form of α2)the same bound on the L2norm of the Ricci tensor. In joint work of Paul with R. Brooks and P. Perry [3], they showed that a set of isospectral metrics in a fixed conformal class on a three-dimensional manifold M3that admits a metric of negative scalar curvature, is compact in the C∞-topology. Note that the result is false if the conformal class admits a metric of positive scalar curvature, since the conformal group of the sphere acts on the round metric to give a non-compact family of isospectral conformal metrics.

Remarkably,Polyakov[49]was able to compute a closed formula for the conformal variation of the determinant when M is two-dimensional: if ˆg=e2wg,then

where K=Kgis the Gauss curvature of g. Notice the right-hand of this formula is the leading order terms of the functional J1in(1.6). In particular,if g=g0is the round metric on S2and we fix the area of ˆg to be 4π,then the Moser-Trudinger inequality(1.4)implies that

In fact,Onofri[45]showed that that C1=0,and that equality occurs if and only if ˆg=f∗g0for some conformal map f:S2→S2.

For a general Riemann surface(M,g)the formula(1.9)defines an action on the space of unit volume conformal metrics, and critical points are precisely those metrics of constant Gauss curvature. In a series of papers [46], [47], Osgood-Phillips-Sarnak used the regularized determinant to study the compactness of isospectral metrics on surfaces,and the existence of extremals of the functional determinant in a fixed conformal class. In an appendix to their paper on the three-dimensional isospectral problem[31], Alice and Paul showed that to get the Osgood-Phillips-Sarnak compactness result,all one needs is the information contained in the heat invariants along with control of the first eigenvalue (as opposed to control of the determinant, which contains much more information).But they soon turned their attention to a paper of Branson and Ørtsed, who had derived a Polyakov-type formula for certain elliptic operators on conformal manifolds of dimension four. This would result in a ground-breaking paper in the Annals that would introduce a new subject and have connections to unexpected areas of mathematics.

In[2],Branson-Ørsted were able to generalize Polyakov technique to four dimensions. A key property that Polykov used was the coformal invariance of the laplace operator in two-dimensions:if ˆg=e2wg,then

In higher dimensions this property fails,but there are other conformally invariant differential operators.For example,the conformal Laplacian

where R is the scalar curvature,is conformally covariant in the sense that

If A=Agis a conformally invariant operator defined on a Riemannian four-manifold(M4,g),then Branson-Ørsted gave a closed formula for the functional

Since the determinant is not scale-invariant we add a normalizing term and consider a normalized version of the functional FA,which satisfies FA[w+c]=FA[w].

The precise formula is quite complicated and takes some time to describe. The first thing to note is that FAcan always be expressed as a linear combination of three universal (i.e., independent of the particular operator) terms. Alice and Paul introduced the convention of labelling these terms I,II,III,hence we can express FAas

where(γ1,γ2,γ3)is a triple of real numbers that depend on the choice of the operator A.Branson-Ørsted calculated these coefficients for several examples of A. For example, If A=L,the conformal Laplacian,then γ1(L)=1,γ2(L)=−4,γ3(L)=−2/3.

Not long after the Branson-Ørsted work, in joint work with Branson [1], Paul and Alice studied the functional FAin the conformal class of the round sphere(S4,g0), with A=L,the conformal Laplacian[1]. They showed that all three functionals I,II,and III,are minimized by the round metric,up to conformal transformations. In particular,

for all conformal metrics g=e2wg0. This was a beautiful generalization of the work of Osgood-Phillips-Sarnak. Moreover, it demonstrated that the variaitonal theory for the regularized determinant in four dimensions was a rich subject with connections to many areas of analysis and geometry.

After the work with Branson,Alice and Paul wrote a seminal paper,“Extremal metrics of zeta function determinants on 4-manifolds”, which appeared in Annals of Mathematics[33]. This paper had two main themes.The first was to establish general existence results for extremals of the determinant functional (1.13) on conformal four-manifold.The second theme, which we will explain in more detail, was the variational aspects of the so-called Q-curvature equation.

In four dimensions there is another example of a conformally invariant operator,known as the Paneitz operator:

where δ is the divergence operator and the curvature term23Rg−2Ric is viewed as an endomorphism of the tangent bundle. The Paneitz operator is conformally convariant in the sense that

compare with(1.11). If addition to the obvious parallel between(1.11) and (1.15), there are geometric reasons for viewing P as the natural generalization of the Laplace operator to four-manifolds. For example,as we saw when discussing the Nirenberg problem,the Laplace operator arises in the formula(1.5)relating the Gauss curvatures of conformally related metrics. In four dimensions, there is a curvature quantity, the “Q-curvature”,defined by

Given two conformal metrics ˆg=e2wg,then their respective Q-curvatures are related by the formula

The parallel with(1.5)is obvious. Moreover,the total Q-curvature is a conformal invariant:

The relevance to the regularized determinant is that the Paneitz operator and Qcurvature appear in the term II of the Branson-Ørsted formula (1.13). Moreover, a first variation calculation shows that

Therefore, II is the four-dimensional analogue of the Liouville energy J1defined on a Riemannian surface. In [33], Paul and Alice gave the first existence result for critical points of II;i.e.,for metrics of constant Q-curvature:

Theorem 1.2. If the total Q-curvatureM4QgdV is less than that of the round sphere, and the Paneitz operator Pgis positive with trivial kernel,then there is a conformal metric ˆg with constant Q-curvature.

The proof used the direct variational method to show that the functional II can be minimized. Also, the triviality of the kernel is a necessary condition for II to have a lower bound.

Over the next several years Alice and Paul would continue working on the analytic and geometric aspects of the Q-curvature. In [34] they proved Liouville-type theorems for entire solutions. In beautiful work with J. Qing [22,23], they studied the total Qcurvature of complete, locally conformally flat (LCF) four-manifolds. Alice would also co-author a series of papers with J.Qing[19–21]that examined a Polyakov-type formula for manifolds with boundary due to Branson-Gilkey. This work lead to the discovery of new conformally invariant boundary operators.

Paul and Alice’s work on the Q-curvature inspired their interest in other higher order geometric variational problems. In a pair of papers with L. Wang, Paul and Alice studied regularity properties of sphere-valued biharmonic maps, and gave a new and more elementary proof of H´elein’s fundamental regularity result for harmonic maps of surfaces[26],[27].

In general,critical points of the regularized determinant(1.13) will be solutions of a fourth order semilinear PDE. However, for a special choice of the constants γiin (1.13)(the actual condition one needs is γ2+12γ3=0), the highest order terms in the Euler equation cancel, and the equation becomes a second order equation in the metric. If we further take γ1=0, then the resulting Euler equation, written as a condition on the curvature of the metric ˆg=e2wg,is

where κ is a constant.The significance of this is the following:if the constant κ>0,and the scalar curvature of the critical metric ˆg=e2wg is positive,then a simple calculation shows that the Ricci curvature of ˆg must be positive. This suggests the idea of finding critical points of FAin order to construct metrics with positive Ricci curvature. This was carried out in joint work Paul, Alice, and the author in [17]. It will be easier to state the main result of that paper if we first describe a parallel development due to Viaclovsky[52].

Given an n-dimensional Riemannian manifold (M,g), then one can decompose the curvature tensor as Riem=W+A∧g,where A is the Schouten tensor,

and ∧is the Kulkarni-Nomizu product. Since the Weyl tensor is conformally invariant,the behavior of the curvature tensor under a conformal change of metric is determined by the Schouten tensor.In his thesis,Jeff Viaclovsky[52]initiated the study of the functionals

When k=2 and n=4 the integral in(1.21) is conformally invariant. In fact, σ2is related to the Q-curvature:

so the total Q-curvature(a conformal invariant)is just a multiple of the total σ2-curvature.

When k>2 but k/=n/2, and if we assume the conformal structure is locally conformally flat,then critical points of(1.21)satisfy

In fact,Branson and Gover showed that conformal flatness is a necessary condition,otherwise additional terms will appear in the Euler-Lagrange equation of(1.21).

Viaclovsky proposed the problem of solving the equations(1.24)(whether they arise variationally or not)as a generalization of the Yamabe problem. They are now referred to as the“σk-curvature equations”, and the problem of finding solutions as the σk-Yamabe problem. Since they are fully nonlinear, one has to impose an ellipticity condition. Although there is now an extensive existence theory for solutions, some basic questions(especially about regularity)remain unanswered.

The connection between the study of the functional determinant in dimension four and the equations introduced by Viaclovsky is the following: the special case of the Euler equation(1.19)is,up to a constant,the equation(1.22). Using the determinant functional,Chang-Gursky-Yang proved

Theorem 1.3([16,17]). Let(M4,g) be a closed Riemannian four-manifold with positive scalar curvature. If

then there is a smooth conformal metric ˆg=e2wg solving(1.22). Moreover,the Ricci curvature of ˆg satisfies 0

This was the first existence result for the σk-Yamabe problem. Moreover, since the conditions are conformally invariant, it is relatively easy to construct examples of manifolds satisfying the hypotheses. Later, Chang-Gursky-Yang would use a version of the σ2-curvature equation in which the right-hand side includes the norm of the Weyl tensor in order to prove a conformally invariant sphere theorem:

Theorem 1.4 ([18]). Let (M4,g) be a smooth, closed four-manifold whose Yamabe invariant Y(M4,[g])>0. If the Weyl curvature of g satisfies

then M4is diffeomorphic to either S4or RP4. Moreover,if equality holds in(1.25)and M4is not diffeomorphic to S4or RP4,then one of the following must be true:

(i)(M4,g)is conformal to CP2with the Fubini-Study metric gFS,or

(ii) (M4,g) is conformal to a manifold which is isometrically covered by S3×S1, endowed with the product metric.

Another area where Paul and Alice have made significant contributions(and continue to do so!) is the theory of Poincar´e-Einstein manifolds. If X is a compact manifold of dimension n+1 with non-empty boundary M=∂X, a metric g defined in the interior of X is called conformally compact if there is a defining function for the boundary (i.e.,a function ρ:X →R such that ρ>0 in X, ρ=0 on ∂X, and dρ/=0 on ∂X) such that ρ2g extends to a Riemannian metric on X. If|dr|g=1 on ∂X then one can show that the sectional curvatures of(X,g)tend to −1 at infinity,and we say that(X,g)is asymptotically hyperbolic.

If g is an Einstein metric,then(X,g)is a Poincar´e-Einstein manifold(or CCE manifold,for “conformally compact Einstein”). The canonical example of a CCE manifold is the Poincar´e ball model of hyperbolic space: in this case X=n+1is the unit ball in Rn+1,and g=4(1−|x|2)−2dx2is the hyperbolic metric. Notice we can take ρ(x)=(1−|x|2)/2 as a defining function, and ρ2g=dx2is the Euclidean metric. It is easy to see that CCE metrics are asymptotically hyperbolic.

The defining function of a conformally compact metric is not unique, and the compactified metrics defined by two different choices of defining function are conformal.Therefore,one can associate to any conformally compact metric g defined in the interior of X a conformal class of metrics on the compact manifold X, and by restricting to the boundary a conformal class of metrics [h=ρ2g|M] on M=∂X. We call [h] the conformal infinity of g. For example,if(X,g)the hyperbolic metric as above,then the boundary conformal class defined in this way is the conformal class of the Euclidean metric restricted to Sn=∂B(0,1)n+1;i.e.,the conformal class of the round metric.

CCE manifolds appear in the Fefferman-Graham theory of conformal invariants[37],and in the AdS/CFT correspondence in theoretical physics. They have sometimes unexpected connections to other areas of mathematics, including some of the topics mentioned above. One of Paul and Alice’s first rsults in this area was joint with J.Qing,and studied the connection between an important invariant of CCE manifold(X,g)known as the renormalized volume,and the topology of X.

Given a CCE metric we can always construct a defining function r for which|dr|≡1 near ∂X. Using expansions of the metric near the boundary (the “Fefferman-Graham expansion”),for ∊>0 the volume of the region X∊={x∈X : r(x)>∊} has an expansion in terms of ∊depending on the parity of the dimension. If n is odd,

where the ci’s are given by integrals of polynomials in the curvature of the induced metric h=r2g|Mon the boundary. If n is even, a logarithmic term appears; to simplify the exposition we will only discuss the odd-dimensional case.

Remarkably,the constant term V in the expansion(1.26)is independent of the choice of defining function, and is therefore a conformal invariant of the boundary (see [37]).When n=3,in[24]Chang-Qing-Yang showed that if then X is homeomorphic to B4,up to a possible finite cover. Moreover,if the constant on the right is improved from 1/3 to 1/2,then X is diffeomorphic to B and ∂X is diffeomorphic to S3.Two of the ingredients of their proof are the sphere theorem of Chang-Gursky-Yang mentioned above,and a formula when n=3 due to Anderson that relates V to the Euler characteristic and the L2-norm of the Weyl tensor.

In subsequent work[25],Chang-Qing-Yang showed that Anderson’s formula is actually a special case of a much more general formula for n odd that expresses the renormalized volume of a CCE manifold in terms of the Euler characteristic and a conformally invariant integral. The integrand is a sum of contractions of the Weyl tensor and its covariant derivatives;when n=5 they gave an explicit formula.

In addition to the conformal Laplacian and Paneitz operator there are other examples of conformally covariant operators. Graham-Zworksi [40] used scattering theory methods on asymptotically hyperbolic manifolds to construct families of conformally invariant operators Pγwith principal symbol the same as (−∆)γ, for γ ∈(0,n). When γ=k ∈(0,n/2) is an integer Pkcorresponds to the operators found earlier by Graham-Jenne-Mason-Sparling, but for non-integer values their construction gives examples of conformally covariant non-local operators. Fractional powers of the Laplacian also appear in various mathematical models of physical phenomena. On Euclidean space one can use the Fourier transform to define (−∆)γ, but Caffarelli-Silvestre [5] showed that for γ ∈(0,1)one can construct these operators by solving a degenerate elliptic extension problem on the upper half-spacethen restricting the solution to the boundary. In joint work of Alice with Maria del Mar Gonzalez[14],they had the beautiful insight that the Graham-Zworski construction and the Caffarelli-Silvestre construction were really the same idea in different guises:properly interpreted,the Caffarelli-Silverstre extension problem was the scattering operator on the upper half-space model of hyperbolic space.This realization allowed them to recast the Caffarelli-Silvestre construction in the framework of CCE manifolds and extend the construction to γ∈(0,n/2).

More recently, Alice has been studying a fundamental question related to the existence theory for CCE metrics. The basic existence question is the following: Suppose we are given a compact manifold with boundary X,and a conformal class of metrics[h]defined on ∂X. Does there exist a CCE metric g+defined in the interior of X,whose conformal infinity is given by[h]? It is now known that there are topological obstructions to existence,but there are important settings where the question is still open. For example,if X=B4is the four-dimensional unit ball,and[h]is a conformal class on S3with positive Yamabe invariant,it is expected that existence always holds.

One approach to this question, proposed by Anderson, is to use a degree theoretic argument combined with a compactness theory for CCE metrics. In very naive terms,the compactness question asks the following: Suppose {(g+)j} is a sequence of CCE metrics on B4, with conformal infinities {}. Suppose further there is a sequence of representatives∈[hj] that converges in the C∞-topology. What can we say about the sequence{(g+)j}? Of course,it is expected that one would need to add assumptions to get a reasonable answer, but the conditions should be naturally connected to invariants of CCE metrics.

In a series of papers of Alice with Y.Ge[12]and Ge and J.Qing[13],they continually refined the compactness theory in four dimensions and explored some very interesting and unexpected applications. The precise statement is somewhat technical,but in a sense optimal. If we view the conformal infinity of a Poincar´e-Einstein metric as the Dirichlet data for a singular boundary value problem, then there is a tensor (the S-tensor) that can be viewed as the Neumann data. The compactness results of Alice with her coauthors roughly says that non-concentration of the L1-norm of S gives good control of a four-dimensional Poincar´e-Einstein metric near the boundary. A slightly more precise statement is the following: Suppose(X4,gj)is a sequence of four-dimensional Poincar´e-Einstein manifolds with conformal infinities(S3,[hj]). Let∈[hj]be a sequence of Yamabe metrics, and assume {˜hj} is compact in the Ck,α-Cheeger-Gromov topology. Then,assuming non-concentration of the L1-norm of S, there is sequence of compactifications=that forms a compact family (up to pull-back by diffeomorphisms that fix the boundary).

In addition to the connection to the existence theory mentioned above,this result has other important consequences. For example, Graham-Lee [39] showed that if [h] is a conformal class on S3that is sufficiently close to the standard conformal structure,there is a Poincar´e-Einstein metric g+in B4whose conformal infinity is [h]. A (non-obvious!)corollary of the work of Chang-Ge-Qing is that there is a neighborhood of the standard conformal structure on S3such that the Graham-Lee extension is the unique Poincar´e-Einstein metric in B4.

Over the last decade or so Paul has returned to his roots in complex geometry,and has applied some of the ideas he helped to develop in conformal geometry CR geometry.Since several of his most significant results occur in three dimensions, we will restrict ourselves to this case. A three-dimensional CR manifold is a triple consisting of a threemanifold M3,a rank two sub-bundle HM⊂TM defined by a one-form θ,and an almostcomplex structure J:HM→HM;i.e., J2=−I. A canonical example is S3⊂C2.

CR manifolds model real hypersurfaces of complex manifolds;in fact,a fundamental question is under what conditions an abstract CR manifold can be embedded into Cn.Burns and Epstein[4]showed that generically,even small perturbations of the the standard CR structure on S3are not embeddable. Kohn gave a condition for embeddability in terms of the eponymous operator □b. In particular, a positive lower bound for the spectrum is sufficient.

It turns out that the conformal laplacian and the Paneitz operator, two differential operators we have already encountered when discussing Paul and Alice’s work in(real)conformal geometry,have counterparts in the CR setting. In this context,the invariance of the CR versions is under transformation of the contact form via=e2fθ. The CR conformal laplacian,like its real counterpart,arises in the study of the CR Yamabe problem,which seeks a change of contact structure of this form for which the Webster scalar curvature is constant.

The CR Paneitz operator was written down by Graham-Gover[38]and Harachi[42],and like its real counterpart is fourth order. In joint work of Paul with S. Chanillo and H.-L.Chiu [35], they proved a remarkable Bochner formula relating the Kohn laplacian to the CR Paneitz operator. As a consequence, if the Paneitz operator is non-negative and the Webster scalar curvature is positive, then the Kohn laplacian has closed range and the CR structure is embeddable. Note that the positivity of the Paneitz operator is a CR-invariant (unlike the positivity of □b). In subsequent work of Paul with J. Case and Chanillo [7] they studied conditions under which positivity of the CR Paneitz operator holds,and used these conditions to give concrete examples(for example,real ellipsoids in C2).

Paul(with A.Malchiodi and J.-H.Cheng)has also shown a surprising connection between the CR Paneitz operator and the CR Yamabe problem[36]. The starting point is a defintion of an ADM mass in the CR setting,defined for asymptotically flat pseudohermitian manifolds. Like the classical ADM mass, it can be expressed in terms of the first non-trivial term in the expansion of of the Green’s function for the CR laplacian. They prove an integral formula for the mass, related to their Bochner formula for the Kohn laplacian. This allows them to characterize the standard CR-stucture on S3as having zero mass.However,in contrast to the classical ADM mass,they constructed CR manifolds with negative mass. Of course,one of the key applications of this analysis is the proof of existence of solutions of the CR Yamabe problem.

As in the real case,there is a curvature quantity associated to the CR Paneitz operator called the Q′-curvature. The total Q′-curvature agrees with the Burns-Epstein invariant up to a divergence term. With various coauthors, Paul has also studied the existence problem for CR structures with constant Q′-curvature (e.g., [8]). The problem is variational, and there is an obvious parallel with Paul and Alice’s work on the regularized determinant in four dimensions that we described above. However,one technical challenge in CR geometry that has no parallel in the real case is the fact that the kernel of the Paneitz operator contains the set of pluriharmonic functions. This is very different that the real(i.e.,elliptic)case.

In closing,I return to my warning at the beginning of this article: it is not exhaustive.A partial list of areas in which Paul and Alice have made significant contributions that I have not touched on would include optimal transportation,minimal surfaces in pseudohermitian geometry, functional inequalities, the Q-curvature equation in dimensions n/=4, and the topology of locally conformally flat manifolds. My goal has been that of a museum visitor who spends their time appreciating a small number of masterpieces,rather than making a cursory tour of the entire collection.

Another, perhaps more serious limitation of my attempt to summarize the work of Paul and Alice is that it fails to convey the influence they have had on the profession through the students and postdocs they have mentored.As a former student who became a collaborator(and close friend),I have benefited from their generosity to their students and from their profound mathematical insights,and both are part of their legacy.