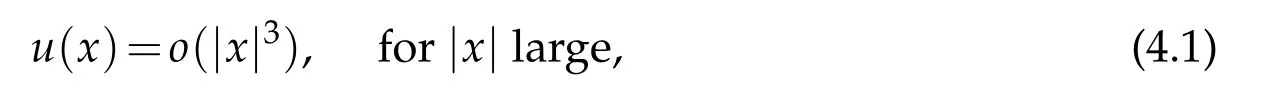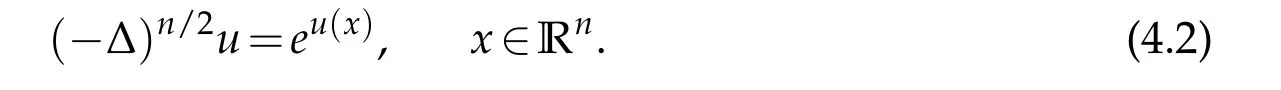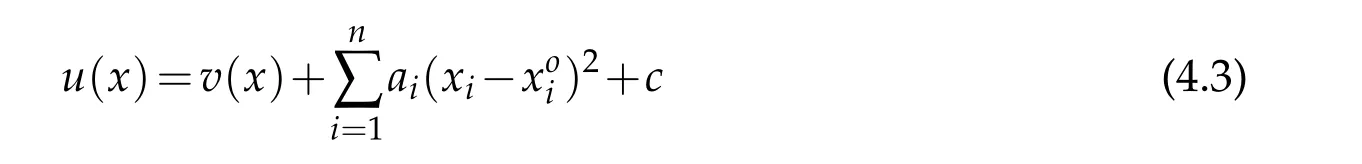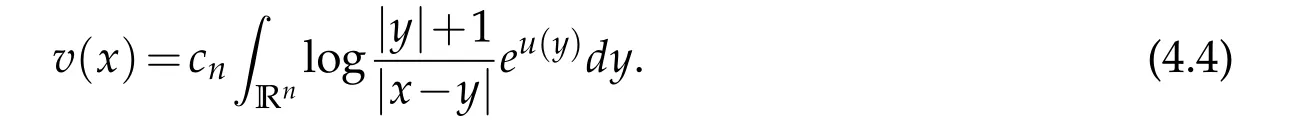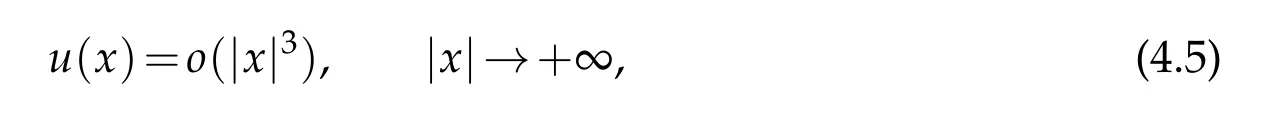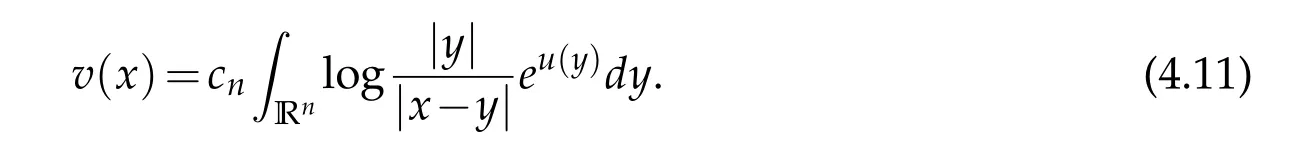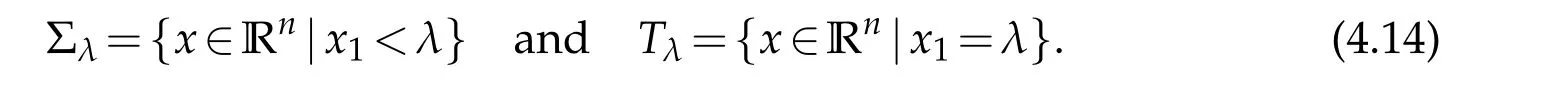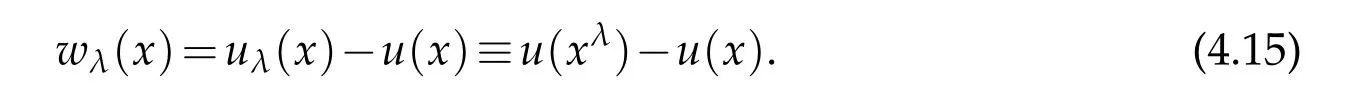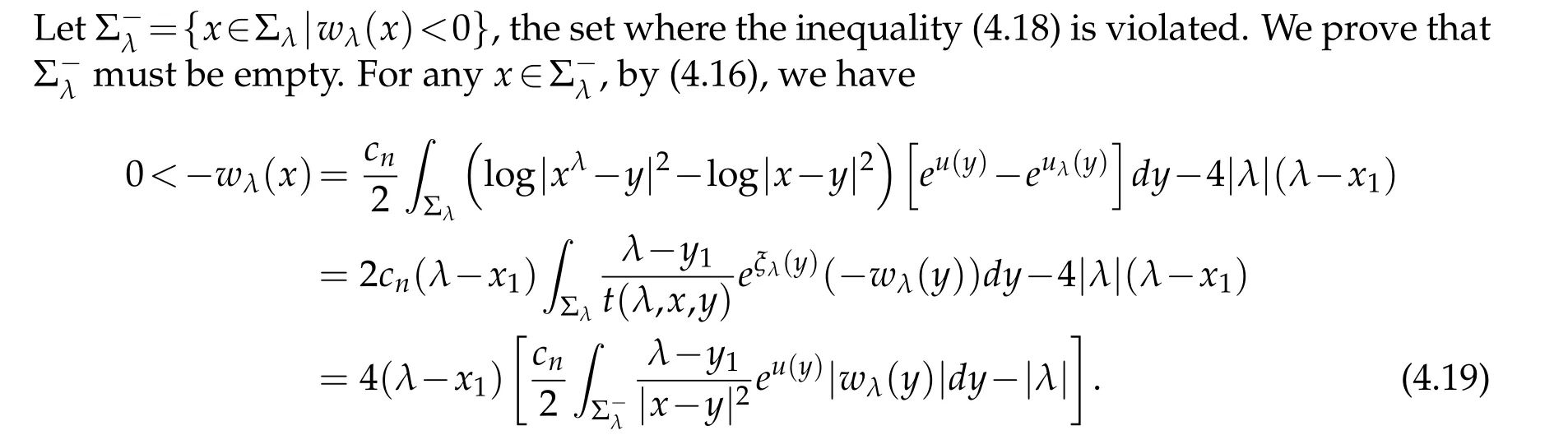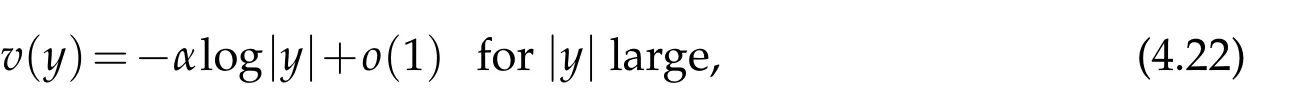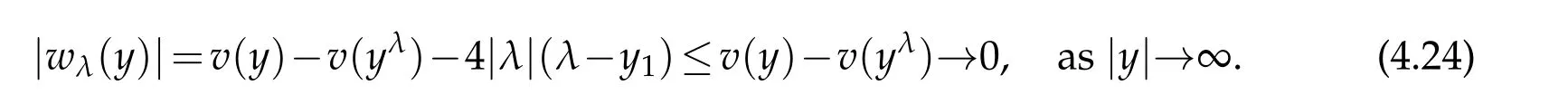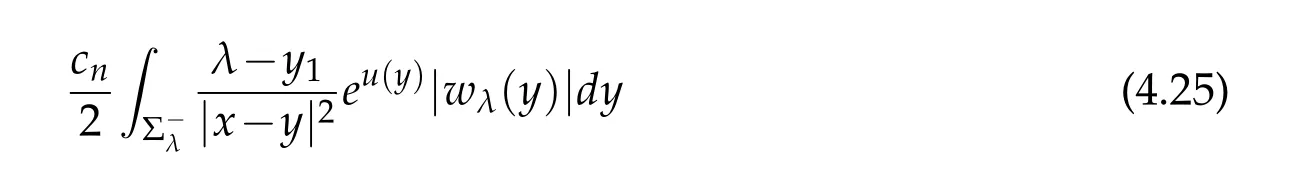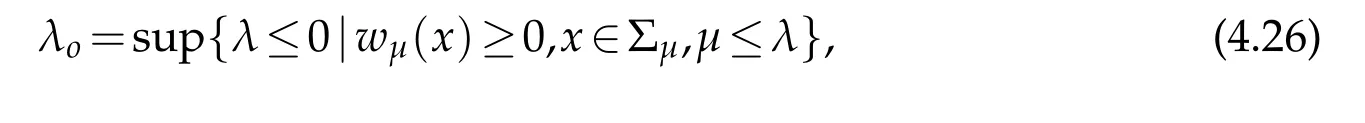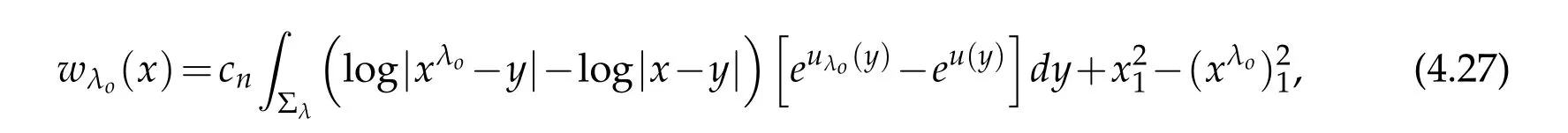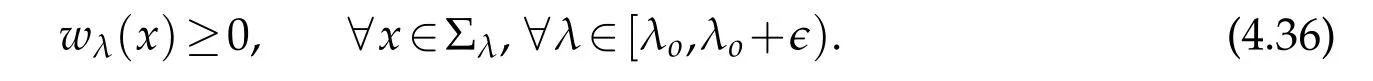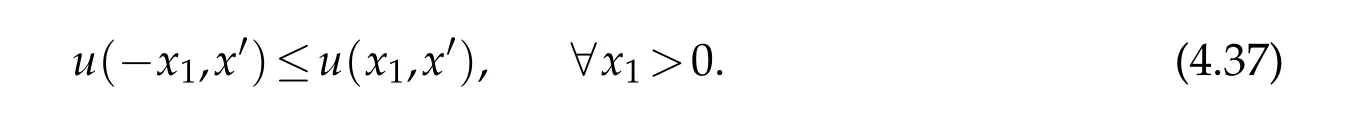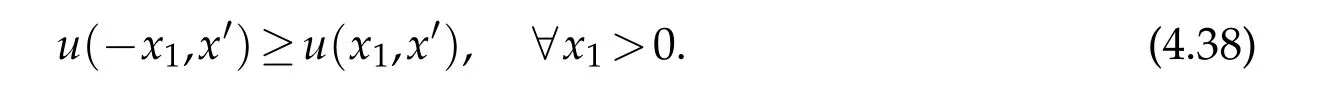Regularity and Rigidity for Nonlocal Curvatures in Conformal Geometry
2020-03-20WenxiongChenandRuobingZhang
Wenxiong Chen and Ruobing Zhang
1 Department of Mathematics,Yeshiva University,New York,NY 10033,USA;
2 Department of Mathematics,Stony Brook University,Stony Brook,NY 11794,USA.
Abstract. In this paper,we will explore the geometric effects of conformally covariant operators and the induced nonlinear curvature equations in certain nonlocal nature.Mainly,we will prove some regularity and rigidity results for the distributional solutions to those equations.
Key words: Regularity,spherical rigidity,nonlocal curvatures,conformal geometry.
1 Introduction
In conformal geometry, a primary goal is to understand both analytic and geometric properties of the conformally covariant operators.Specifically,let(Mn,g0)be a Riemannian manifold of dimension n and equipped with a conformal structure[g0]. For example,in the case of second order differential operators,the most classical conformally covariant operator is the conformal Laplacian. For n≥3,it is defined as


To start with, we introduce some background materials of the conformally compact Einstein manifolds and the precise definition of the nonlocal curvature Q2γ.
Definition 1.1. Given a pair of smooth manifolds(Xn+1,Mn)with Mn≡∂Xn+1,we say a complete Einstein metric g+on Xn+1is conformally compact Einstein if it satisfies

and there is a conformal metric=u2g+which smoothly extends to the boundary Mnwith a restriction

The conformal manifold(Mn,[h0])is called the conformal infinity.
Establishing effective connections between the conformal structure of the conformal infinity(Mn,[h0])and the Riemannian structure of the Einstein filling-in(Xn+1,g+)is always a central topic of conformal geometry and the theory of AdS/CFT correspondence.A crucial tool in understanding the above structure is the conformally covariant operators defined on a conformally compact Einstein manifold. Due to Graham-Zworski[16]and Chang-Gonz´alez[5],there are a family of conformally covariant operators called the fractional GJMS operators(see[2,5]).Specifically,in the context of Definition 1.1,we define the operator as below.
Definition 1.2(Fractional GJMS operator). Given any real number γ∈(0,),
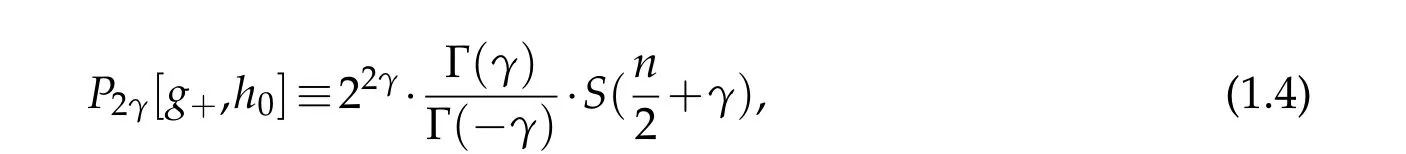
where S is the scattering operator which is essentially a Dirichlet-to-Neumann operator (we refer the reader to [5] and [16] for the more detailed definition of the scattering operator).

Moreover,it follows from the computations in[16]that the following conformal covariance property always holds in the critical case: if ˆh=e2uh0then,

The above relations are essentially given by the meromorphic property of the scattering operator, see [16] for more details. In the literature, there are extensive studies in the analytic aspect regarding the nonlocal operators and curvatures in recent years. However, in the literature, so far the geometric properties and applications have not been well and enough explored even in the simplest case. Conformally flat manifolds are the most natural objects such that the nonlocal operators can play their effective roles.
In a recent paper[28],the second author has obtained some topological obstructions for the manifolds admitting conformally flat metrics with positive nonlocal curvatures.Moreover, in the lower dimensional case, the second author proved some topological rigidity theorems for the conformally flat manifolds (Mn,h) with positive nonlocal curvatures. In our current paper, we will further explore the metric aspect of the nonlocal curvatures. More precisely, we will prove some isometric rigidity theorems under the assumption that the nonlocal curvature of the critical order Qnis a positive constant.
1.1 Main results
In this section,we will present our main theorems.We start with a regularity and rigidity theorem for the distributional solutions to the critical order Yamabe equation in Rn.
Theorem 1.1. Given any integer n≥2,let u be a solution to
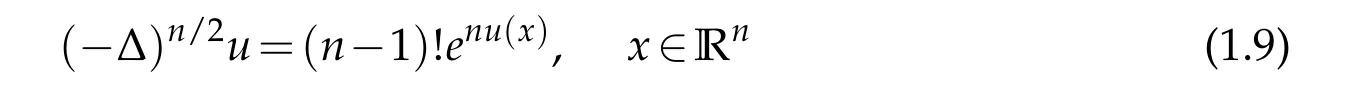
in the distributional sense which satisfies
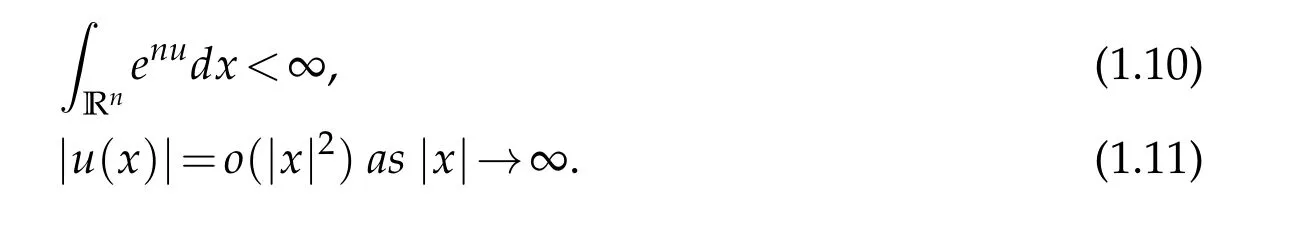
Then there exists some λ>0 and x0∈Rnsuch that

In particular,u is smooth in Rn.
Remark 1.1. It is well known that there are examples of solution to(1.9)which are not of the form

When n=4,Chang and the first author proved in[4]that there are non-standard radial solutions satisfying

with the asymptotic behavior

Such counterexamples tell us that the growth rate condition in Theorem 1.1 is optimal.
A similar classification result was first obtained by Chen-Li in [13] in the case n=2 under a weaker condition

Chang and Yang proved the rigidity result in [9] for higher dimensions under stronger decaying condition

for some smooth function w defined on Sn. In [23], for dimension n=4, Lin weakened condition(1.17)to
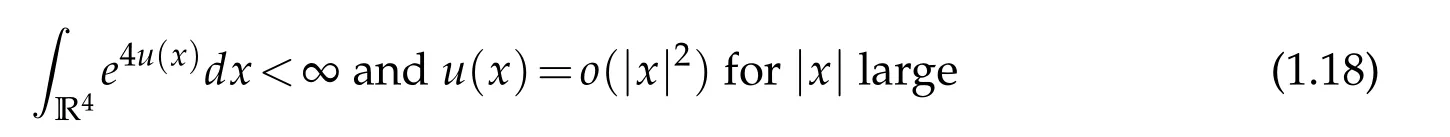
and classified the solutions.In[26],Wei and Xu generalized Lin’s result to all even dimensions. Xu obtained in[27]the rigidity result in all dimensions under a stronger regularity assumption u∈C∞(Rn). As a comparison,in Theorem 1.1,we only need to assume that equation(1.9)holds in the distributional sense.
Next we consider the geometry of the nonlocal curvature Q3in the case n=3,where the curvature Q3is deeply connected to the topology of the underlying conformally compact Einstein manifold(X4,M3,g+)via the following version of the Chern-Gauss-Bonnet formula. In our specific context of conformally compact Einstein manifold(X4,M3,g+),it is a combined result due to [14] and [8] that the following generalized Chern-Gauss-Bonnet formula holds,
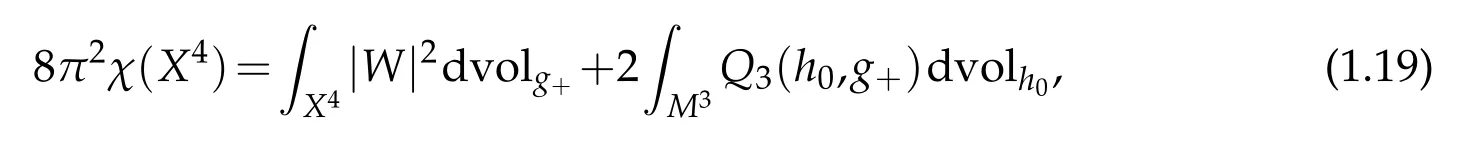
where(M3,[h0])is the conformal infinity.In a special context that the Einstein filling-in is specified as a hyperbolic manifold with constant sectional curvature −1,the second author proved in[28]a conformal sphere theorem regarding positive Q3.
Theorem 1.2 (Zhang, 2018). Let (M3,g) be a closed locally conformally flat manifold with Rg>0 and Q3>0,then(M3,g)is conformal to S3or RP3.
We also refer the reader to[28]for more geometric and topological rigidity theorems on the nonlocal curvatures. Based on the conformal sphere theorem, we can obtain an isometric sphere theorem by assuming the nonlocal curvature Q3is a positive constant.
Theorem 1.3. Let(M3,g)be a closed locally conformally flat manifold with

then (M3,g) is isometric to the round sphere S3or the projective space RP3with constant sectional curvature secg1≡1.
Proof of Theorem 1.3. Since we have assumed

by Theorem 1.2, (M3,g) is conformal to S3or RP3. In particular, applying the stereographic projection,one can write

such that

and u(x)→−2log|x| as |x|→+∞. Moreover, the following curvature equation holds globally in R3,

Theorem 1.1 implies that g is isometric to the standard metric on S3or RP3with constant sectional curvature+1.
We should emphasize that in the nonlocal cases of the above isometric rigidity theorems,we need to specify the Poincar´e-Einstein filling-in which are hyperbolic manifolds in our context. Otherwise,constant Qndoes not imply the sphere theorems. A standard example is the following AdS-Schwarzschild space.
Example 1.1(The AdS-Schwarzschild space). Let(M3,h0)≡(S1×S2,dt2⊕g1),there are a family of Einstein metrics on the topological product R2×S2called the AdS-Schwarzschild metrics,which has the explicit expression


1.2 The analysis of the fractional GJMS operators

Plugging(1.27)into the conformal covariant equation(1.8),we have the nonlocal Yamabe equation

Based on the above discussion, now the nonlocal Yamabe equation on the universal covering space is given by the following semi-linear equation
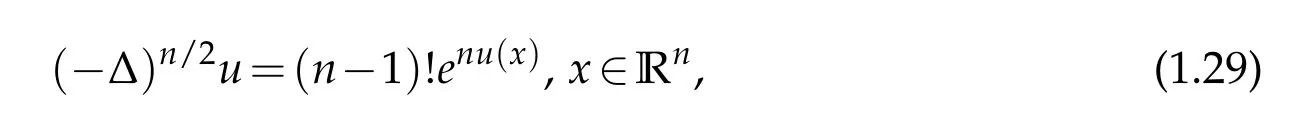
where the dimension n≥2 is an arbitrary positive integer. When n is even,(−∆)n/2is a poly-harmonic operator;while n is odd,it is a nonlocal fractional operator.For n=2m+1,we define

with
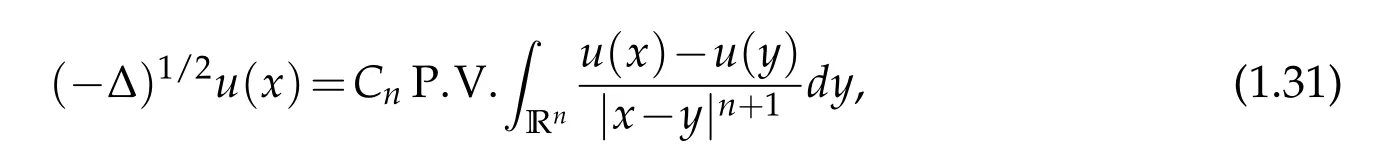
where“P.V.”stands for the Cauchy principal value. We say that u is a solution of(1.29)in the distributional sense if
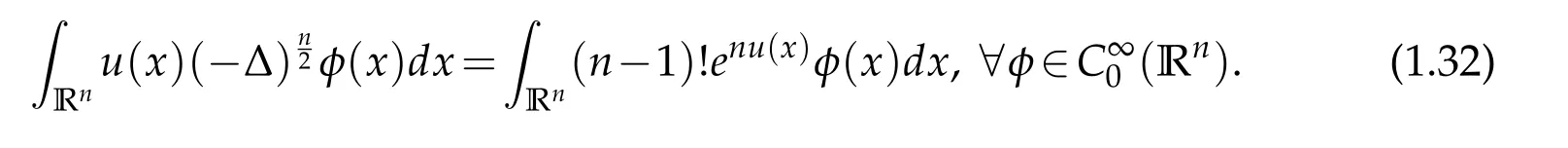
In the case when n is even,first a Pohozaev type identity was obtained and employed to derive the exact asymptotic behavior of the solution u near infinity,then the method of moving planes was applied to prove the radial symmetry of u,and finally,by the uniqueness theory of ODEs,the classification of solutions was established[13,23,26].All these are based on local analysis and are no longer at our disposal in the nonlocal setting when the space dimension n is odd. To our knowledge, there is no corresponding Pohozaev identities except in the case u is identically zero outside a finite domain (see [25]) and the ODE theory are no longer applicable to radial solutions for fractional equations[15].To overcome these difficulties,we apply the method of moving planes and moving spheres in integral forms to classify solutions and unify the proofs in all dimensions. As is known to the people in this area,when applying the usual method of moving planes,the higher the order of the operator,the more analysis is required. While its counter part in integral forms treat all orders,including fractional orders indiscriminately.
The method of moving planes in integral forms was introduced in[12],and since then it has been applied widely to obtain symmetry,monotonicity,non-existence,and classification of solutions for various higher order and fractional order equations. However, the equation here is the so called “critical order” (the order of the operator is the same as the dimension of the space)where the fundamental solution is in the form of logarithm,hence one needs to approach it in an entirely different manner.
1.3 Outline of the proof of Theorem 1.1
The proof of our main classification result(Theorem 1.1)is rather involved,so we outline its structure here.
First, we introduce some notions which naturally appear in our proof. When n is odd, for the higher order fractional Laplacian, there are several equivalent definitions.For instance,when n=3,as we mentioned before,one can define

or by using a single integral(see[22])
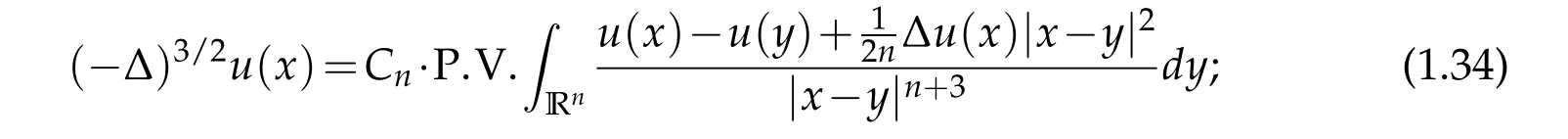
or via Fourier transform
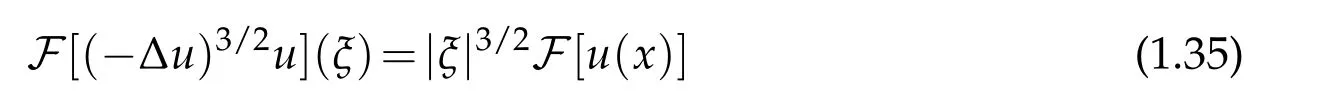
for u∈S,the Schwartz space of rapidly decreasing C∞functions in Rn;and in this space,one can show that all the above three definitions are equivalent. One can extend this operator to a wider space of distributions.
Let
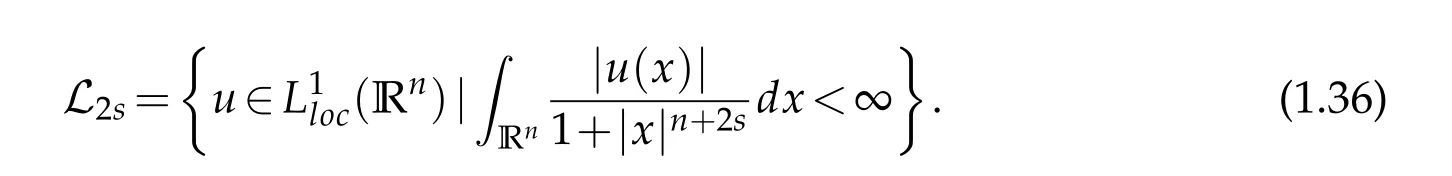
Then in this space,one can define(−∆)su as a distribution by

In order the integral on the right to converge,one requires u∈L2s.Hence,throughout this paper,for odd integer n,we assume that the solution u of(1.29)is in Ln.For a solution u of equation(1.29),let

then one can easily verify that

Hence for the simplicity of writing,in the sequel,we consider
under the condition
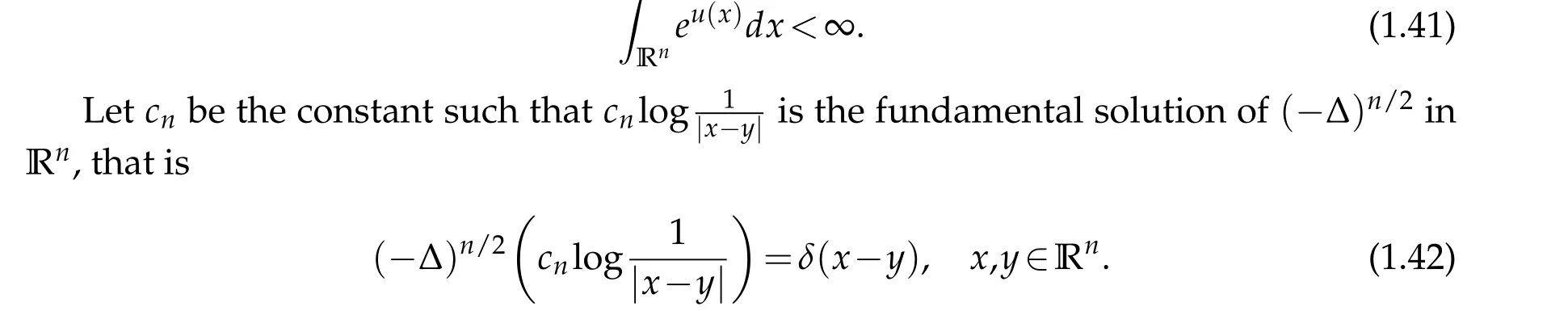
Let
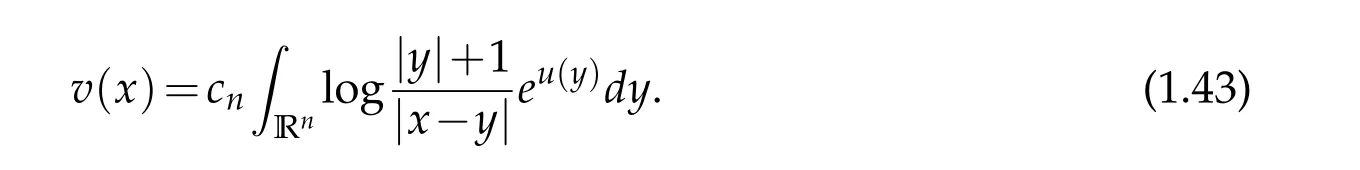
We first consider the case where
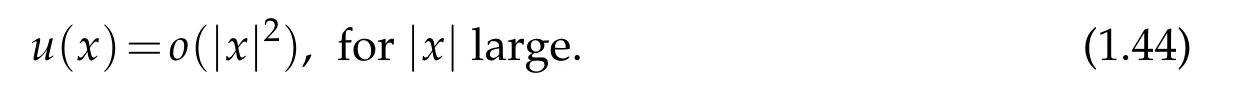
We only assume that u ∈Lnbe a distributional solution,it is locally integrable,but may not be locally bounded. Without local boundedness assumptions on u, v(x)may not be well defined for every x ∈Rnand it may even be unbounded locally. We will first prove that it is locally integrable and then in Ln. Through a quite complex process involving several new ideas,we prove that

is bounded from above uniformly in Rn,and
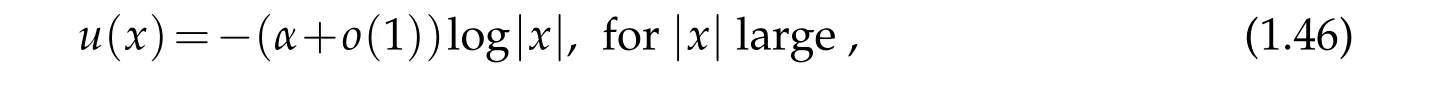
where

The asymptotic behavior of u near infinity depends on the value of α, and to determine it,in the case when n is even,it was done by using Pohozaev identities(see[23,26]).However,when n is odd, due to the nonlocal nature of the fractional operator(−∆)n/2,there are no such identities. To circumvent this nonlocal difficulty,we employ some new ideas. We first apply the method of moving planes in integral forms to deduce α ≥2n, then use the method of moving spheres in integral forms to prove α≤2n and thus arrive at
Proposition 1.1. Under condition(1.44),we have that

With this exact value of α,we will be able to apply the method of moving spheres again to classify all the solutions and establish Theorem 1.1.
In Section 2 and 3,we will focus on the case u(x)=o(|x|2). The asymptotic behavior and regularity of distributional solutions will be derived in Section 2, while the classification of solutions will be established in Section 3. In Section 4,we will consider the case u(x)=o(|x|3)and obtained symmetry of solutions.
2 Asymptotic behavior of distributional solutions when u(x)=o(|x|2)
In this section,we investigate the asymptotic behavior and the regularity of the distributional solutions and establish.
Theorem 2.1. Assume that u∈Lnis a distributional solution of equation(1.40)and

Then u(x)is continuous,differentiable,uniformly bounded from above in Rn,and
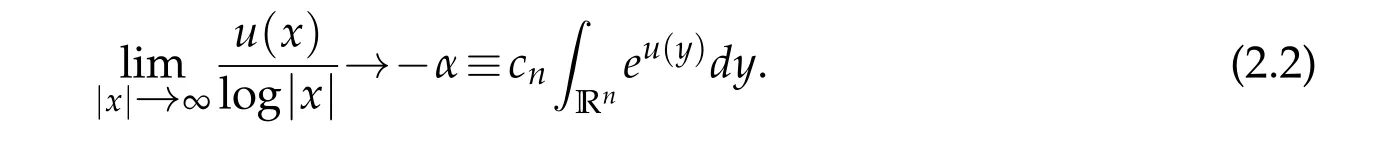
The proof of this theorem is quite complex. It consists of 9 lemmas. Now we give an outline of the proof as follows.
Outline of the Proof. Let
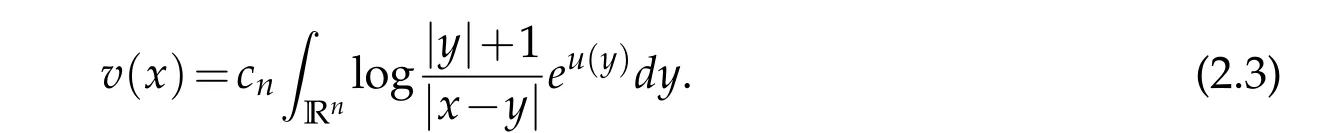
Without assuming that u is locally bounded,this v(x)may not be defined everywhere.We first show that it is locally integrable and in Ln,and then it satisfies the equation

in the sense of distributions.
Let w=u−v,then

Applying the Fourier transform to this temper distribution w,we deduce that w(x)must be a polynomial.
It is elementary to show that
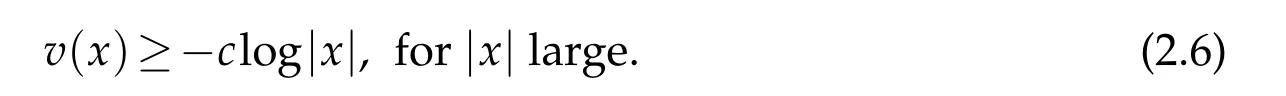
This together with the condition

imply that w has to be a first degree polynomial,and hence

Combining the finite volume assumption

and(2.6),we derive that all aimust be zero and
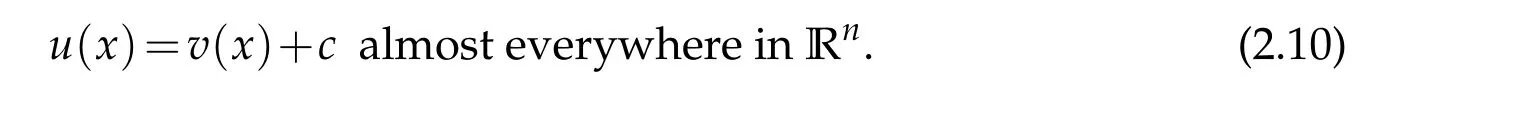
Based on this, we are able to estimate u(x) and prove that it is uniformly bounded from above in Rn. This is a crucial step involving some interesting ideas. Only after this,can we derive that v(x) is defined everywhere, continuous, and differentiable, and so does u(x).
Under the global bounded-ness(from above)of u(x),we derive

which apparently also holds for u(x). This is a needed behavior later in carrying out the method of moving planes and moving spheres to classify the solutions.
In the following,we state the lemmas and present their proofs.
Lemma 2.1. v(x)is in Ln,that is,v∈L1loc(Rn),and

Proof. We first prove that v(x)is locally integrable. For any given R>0,we show that

To this end,let us define
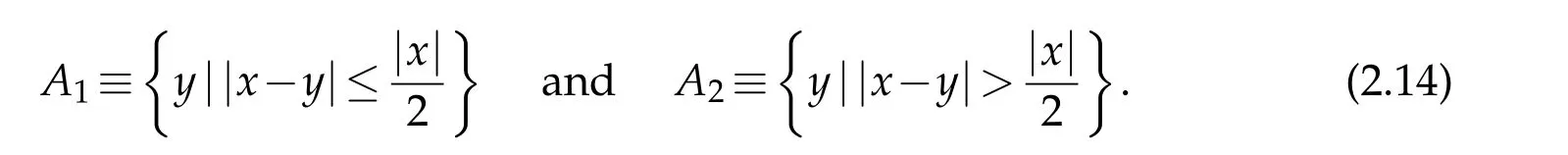
Then it follows that
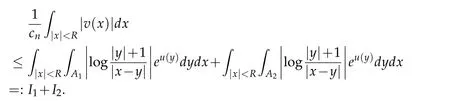
For|x| hence Therefore For|x| while on the other hand It follows that and consequently Combining(2.15),(2.17),and(2.21),we arrive at(2.13). Now the remainder is to show that For each x∈Rn,let We have that Consequently, It follows that Choose R≥2. For|x|≥2 and|y|≥2, and hence For|y|≤2, Combining(2.29)–(2.31),we derive It follows that Now,(2.22)is a direct consequence of(2.24),(2.27),and(2.33). This completes the proof of the lemma. Lemma 2.2. v(x)satisfies in the sense of distribution.Proof. By the definition of the distributional solutions, it suffice to show that, for any φ∈C∞0(Rn),it holds Using the fact that where K is the (compact) support of φ(x), and by a similar argument as in the proof of the previous lemma,one can exchange the order of integrations on the left hand side of(2.35)to arrive at the right hand side. This completes the proof of the lemma. Based on Lemma 2.2,w=u−v is n/2-harmonic in Rn,i.e in the sense of distributions. Lemma 2.3. If a tempered distribution w(x)is s-harmonic in Rnfor some positive real number s,then it is a polynomial. Proof. The proof is similar to that in[10]in which 0 Since w is a tempered distribution,it admits a Fourier transform F(w). We will show that F(w) has support at the origin, hence it is a finite combination of the Dirac’s delta measure and its derivatives. Therefore w is a polynomial(see for instance[17]). In fact,from and the fact that we observe that(−∆)sw=0 means that for any ψ∈S We claim that Now,since w is a tempered distribution and from(2.40),we have This implies that and thus we complete the proof. Lemma 2.4. We have for some positive constant c1. Proof. For|x|≥2 and|y|≥2, hence Therefore for|x|≥3 This completes the proof of the lemma. Lemma 2.5. Assume that u is a distributional solution of(1.40)and Then for some constant C,where Proof. Since u ∈Ln, w(x)=u(x)−v(x) is a tempered distribution,and hence by Lemma 2.3,it is a polynomial. Condition(2.47)implies that w(x)is of at most degree one. Then under the finite volume assumption (1.41) and Lemma 2.4, w(x) has to be a constant.This completes the proof of the lemma. Lemma 2.6. Assume that u is a distributional solution of(1.40)and Then for any point xo∈Rn,we have As a consequence,there exists a constant A1,such that Express Here From condition(2.53), Changing the order of integration, one can easily show that there is a positive constant C1,such that and one can also verify that there is a positive constant C2,such that For x∈B1(xo)and y∈B2(xo), Consequently, the first integral in (2.57) is uniformly bounded from below. Hence by(2.57),there is a constant A,such that Then it follows from(2.54)that Let Then again by Jensen’s inequality,we derive,for any b>0 Now letting γ=ab,we complete the proof of the lemma. Lemma 2.7. Assume that u is a distributional solution of(1.40)and Then u(x)is bounded from above,that is there exists a constant C,such that Proof. Entirely similar to the proof of(2.62),one can show that,for all xo∈Rn, It follows that,for any x∈B1/2(xo), Applying(2.68)and Lemma 2.6,for any x ∈B1/2(xo),we have that u(x)≤C. Since xois arbitrary, we conclude that for every x ∈Rn, u(x)≤C. This completes the proof of the lemma. Lemma 2.8. Assume that u is a distributional solution of(1.40)with and u(x)=o(|x|2). Then u is continuous and differentiable. Based on Lemma 2.7,u is bounded from above,then it is elementary to show that is continuous and differentiable,and so does u(x). Lemma 2.9. As|x|→∞ Hence Proof of Lemma 2.9. Express where I1,I2,and I3are integrals in the following 3 regions respectively: In the following,we use C to denote various constants that are independent of x. i)In D1,we have To see this, one may consider two cases: |y|≤2|x| and |y|>2|x|. Moreover, it follows from(2.76)that ii)By Lemma 2.7,u is uniformly bounded from above in Rn,therefore,in D2we have It follows that iii)In D3,for each fixed R, Consequently,due to bounded-ness of the total volume, Combining(2.77),(2.78),and(2.80),we arrive at This completes the proof of the lemma. In this section, we will prove the main classification result and complete the proof of Theorem 1.1 Due to the local bounded-ness of u(see Theorem 2.1)and by Lemma 2.5,we can also write and we still denote then Theorem 2.1 implies We will show that α=2n, in two stages. First, using the method of moving planes in integral forms,we will prove the following inequality. Lemma 3.1. Let α be the constant defined in(3.2). Then it holds that Proof. Suppose that α<2n, then we will prove that u is radially symmetric about any point by the method of moving planes,hence it has to be a constant,this would contradicts the equation. In order to apply the method of moving planes, we need the solution to decay fast enough near infinity. However at this moment, we do not know the exact value of α. To circumvent this difficulty,we make a Kelvin transform centered at a given point xo. Let where is a constant,and γ=2n−α>0. Let Let xλ=(2λ−x1,x2,···,xn)be the reflection of x about the plane Tλ,and Here we have applied the mean value theorem to both where t(λ,x,y)is valued between|xλ−y|2and|x−y|2,while ξλ(y)is betweenλ(y)and(y). Now we describe the main steps. Step 1. We show that for λ sufficiently negative, by demonstrating that,the set where the inequality is violated, In this step,we only need the following consequence of inequality(3.9): In a usual process of the method of moving planes in integral forms,one simply take the Lqnorm of both side of inequality(3.13)(see for example,[12]and[11]). However, this does not work in our case,because wλ(x)is not integrable in the whole space. The other difference is the presence of the function(λ−x1) on the right hand side. To circumvent this difficulty,we first turn(3.13)to due to the upper bounded-ness ofin Σλ(this bound may become large as λ comes closer to 0,however,for all λ≤−co<0,the bound is uniform). Applying first the Hardy-Littlewood-Sobolev and then Holder inequalities to(3.14),we derive Here q is chosen close to n,so that the integral in converges. Since for λ sufficiently negative,we can make It follows from(3.15)that Step 2. Inequality (3.20) provides a starting point to move the plane Tλ, from which we move the plane toward the right to its limiting position as long as(3.20)holds. Let We prove that λo=0. Otherwise,if λo<0,then from one can see that Based on this,using(3.15),and going through a similar argument as in Step 2 of the proof for Proposition 4.2,we can deduce that,there exists ∊>0,such that This contradicts the definition of λo. Therefore,we must have λo=0 and thus complete the proof of Lemma 3.1. Then we apply the method of moving spheres in integral forms to prove the converse direction. Lemma 3.2. Let α be the constant defined in(3.2). Then it holds that Proof. We will use the method of moving spheres in integral forms to rule out the possibility that α>2n. In the case α>2n,we will show that To this end,we first establish inequality(3.28)for sufficiently large λ,then we move(more precisely,shrink)the sphere Sλ(xo)as long as(3.28)holds to its limiting position.The condition α>2n enable us to shrink the sphere all the way to its center and thus arrive at(3.28)for all positive real value λ. Based on(3.28),due to the arbitrariness of the center xo,and through an elementary calculus argument,we will deduce that ∇u(x)=0 at any point x∈Rn,and hence u must be constant. This would contradicts the equation. Without loss of generality,we may take xo=0 and write uλ,0(x)as uλ(x).In order that u and uλtake the same form,we express Then by a straight forward calculation,one can verify that with γ=α−2n>0.Consider Then by a long,but straight forward computation,we derive where Step 1.We show that for λ sufficiently large, Applying the Hardy-Littlewood-Sobolev and Holder inequalities, we arrive at, for some q>0,Taking into account of the asymptotic behavior We prove that λo=0.Suppose in the contrary,λo>0,we argue that one can shrink the sphere further(just a tiny bit)while maintaining inequality(3.34). This would contradict the definition of λo. In a small neighborhood of 0,wλois negatively bounded away from 0,which can be seen from, the right hand side of which approaches −∞as |x|→0. Hence by (3.40), for any δ>0,there exists cδ>0,such that Consequently, due to the continuity of wλwith respect to λ, there exists an ∊>0, such that letting δ be sufficiently small,we have Let x1→λ,then ξ→y and we arrive at This implies that and since y is any point in Rn, u must be constant. This contradicts equation(1.40)and completes the proof of Lemma 3.2. Combining Lemmas 3.1 and 3.2, we obtain Proposition 1.1. Then we will use the method of moving spheres to classify the solutions,which completes the proof of Theorem 1.1. Proof of Theorem 1.1. By Lemmas 3.1 and 3.2,we have α=2n,and hence(3.32)becomes Similar to the proof of Lemma 3.2,we can still show that,for λ sufficiently large, which approaches −2nlogλ−u(0)as x→0. This quantity is obviously positive for sufficiently small λ. Therefore,in this case,we must have λo>0. So far,we have shown that,for each y∈Rn,there is a λy>0,such that and,in particular,for y=0, In(3.54),fix y and let|x|→∞, Similarly,(3.55)yields For|x|large,via Taylor expansion at y in(3.54),and taking into account of(3.56),we have Similarly,(3.55)and(3.57)lead to Combining(3.58)and(3.59),we deduce Integrating yields Since f is positive,the constant a must be positive,hence we can write Therefore Noticing that,for any constant c,u+c also satisfies identity(3.54),we obtain Finally,taking into account of the total volume: we are able to determine constant c and arrive at the conclusion of Theorem 1.1. This section is to study the symmetry of the solutions u satisfying the asymptotic growth rate u=o(|x|3). To begin with,we have the following rigidity result. Proposition 4.1. Assume that is a distributional solution to Then it holds that for some constants ai≤0 and c∈R,where Proof. Based on Lemmas 2.3 and 2.4 and under the assumption w must be a second degree polynomial. After rotating the coordinates and completing the square,we have Now, due to the bounded-ness of the total volume and Lemma 2.4, all aimust be non-positive. This completes the proof of Proposition 4.1. In the following, we will apply the method of moving planes in integral forms to obtain the symmetry of solutions. Proposition 4.2. Assume that u is locally bounded. Under the growth assumption u=o(|x|3)as|x|→+∞,if ai<0,then u(x)is symmetric and monotone decreasing in xiabout the center xi=x. Before carrying out the method of moving planes,we need the regularity and asymptotic behavior of the solutions as stated in the following. Proposition 4.3. Assume that u∈Lnis a distributional solution of Eq. (1.40)and Further assume that u is locally bounded from above. Then u(x)is continuous,differentiable,uniformly bounded from above in Rn,and The proof is similar to some parts of the proof of Theorem 2.1,and it is much simpler in the current case. Under the assumption that u be locally bounded from above,one can derive immediately that is well defined for all x ∈Rn, continuous, and differentiable, so does u(x). Now by the finite total volume condition,we can also express The proof of the uniform upper bound of u(x) is similar to the proof of Lemma 2.6 and 2.7,and the asymptotic behavior comes directly from Lemma 2.9. Notice that due to a technical difficulty(see the proof of Lemma 2.6),we are not able to obtain the uniform upper bound for u(x)without assuming the local upper bound for u(x). Proof of Proposition 4.2. In the following,we let Without loss of generality,we may assume that then where P(x′)is a polynomial of x′=(x2,···,xn). We will apply the method of moving planes in integral forms to show that u(x) is symmetric in x1variable about the center x1=0, and at mean time, we derive that it is monotone decreasing from the center. Let Let xλ≡(2λ−x1,x2,···,xn)be the reflection of x about the plane Tλ,and Then it holds that Here we have applied the mean value theorem to and t(λ,x,y)is valued between|x−y|2and|xλ−y|2. Step 1.We show that for sufficiently negative λ, Here we have applied the mean value theorem to both and t(λ,x,y)is valued between|xλ−y|2and|x−y|2,while ξλ(y)is between uλ(y)and u(y).Since for each fixed λ, Therefore the integral is bounded,and this bound will not increase as λ becomes more negative. It follows that for sufficiently negative λ, the right hand side of (4.19) is negative,which implies thatis empty. Step 2.Step 1 provides a starting point to move the plane Tλ. Now we move the plane toward the right as long as inequality(4.18)holds to its limiting position. More precisely,let and we will show that λo=0 using the contradiction argument. Suppose λo<0, we show that the plane can be moved a little bit to the right while inequality(4.18)is still valid,which would contradict the definition of λo. From the expression we see that that is, This contradicts the definition of λo. Therefore, we must have λo=0. So far, we have shown that By using an entirely similar argument and starting moving the plane from near x1=+∞to the left to its limiting position,we can show that Combining (4.37) and (4.38), we conclude that u is symmetric about the origin with respect to x1,and thus completes the proof of Proposition 4.2. Acknowledgments The second author is partially supported by the National Natural Science Foundation of China(Grant No. DMS-1906265).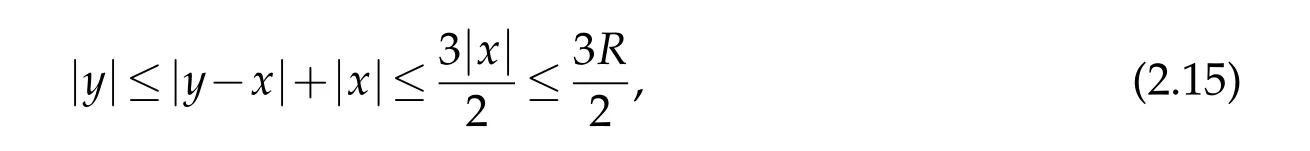

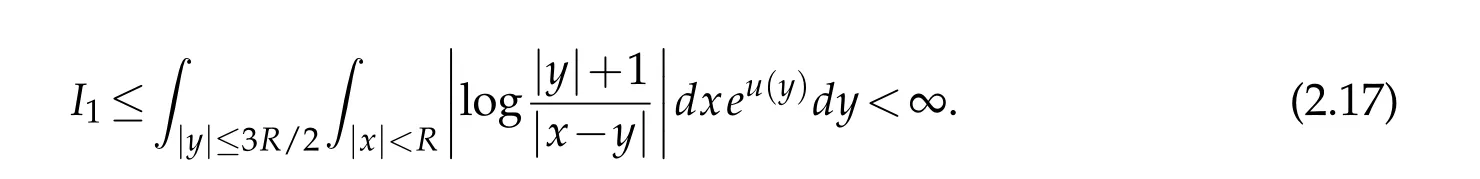

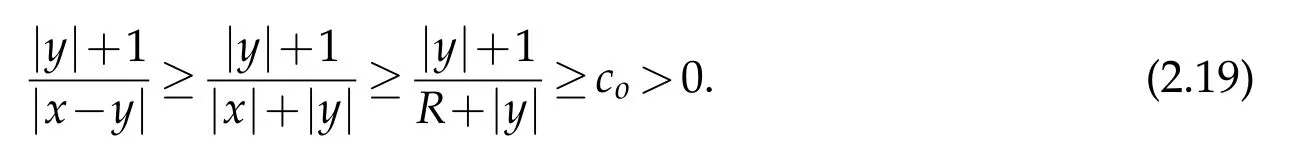
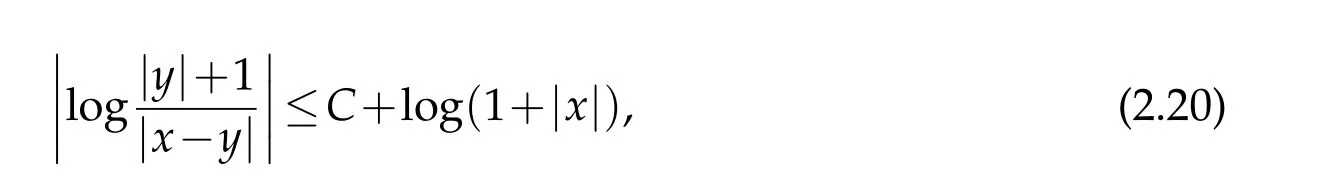

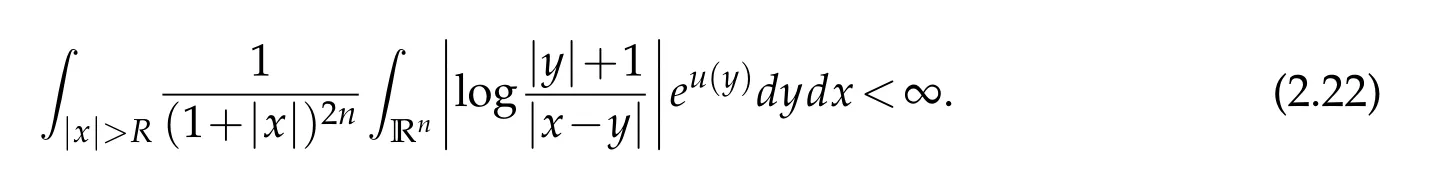
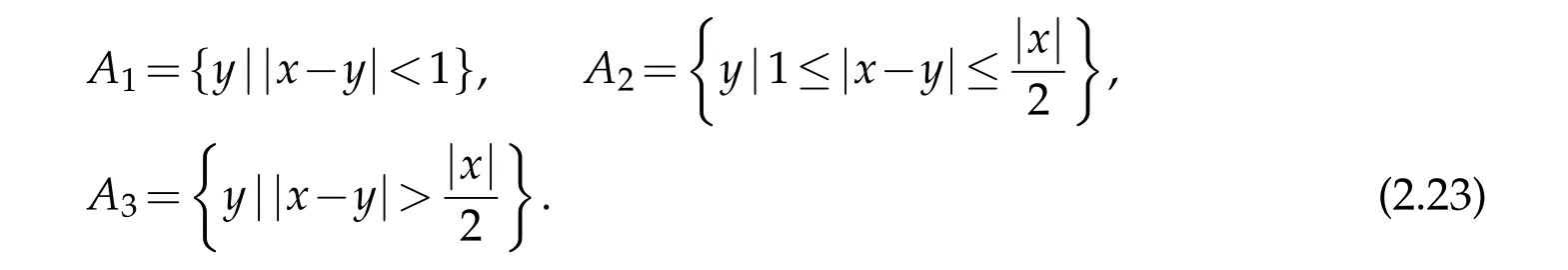
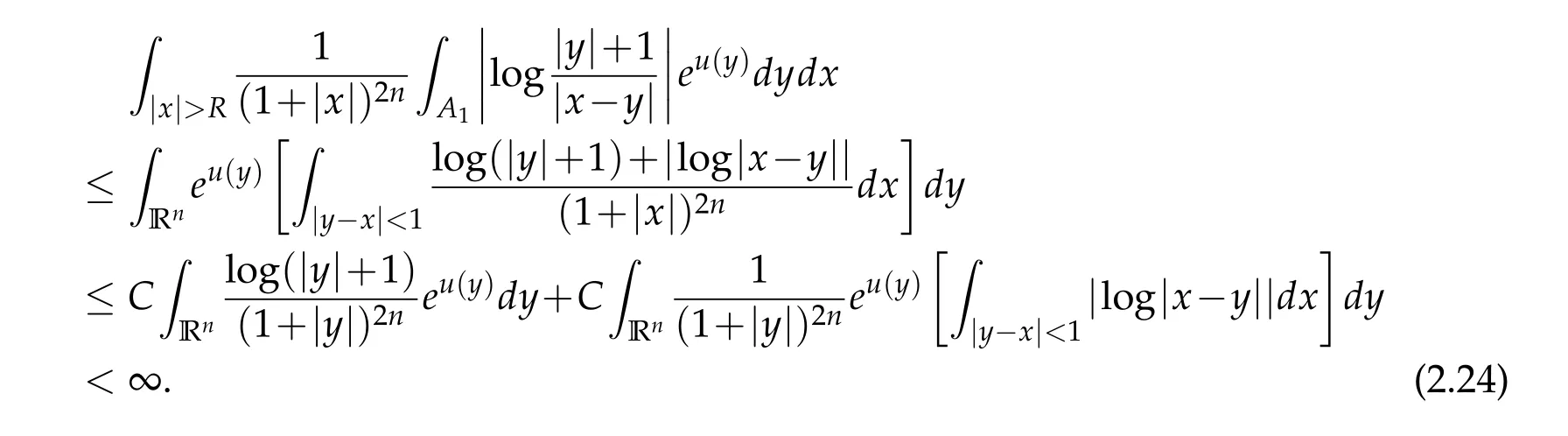
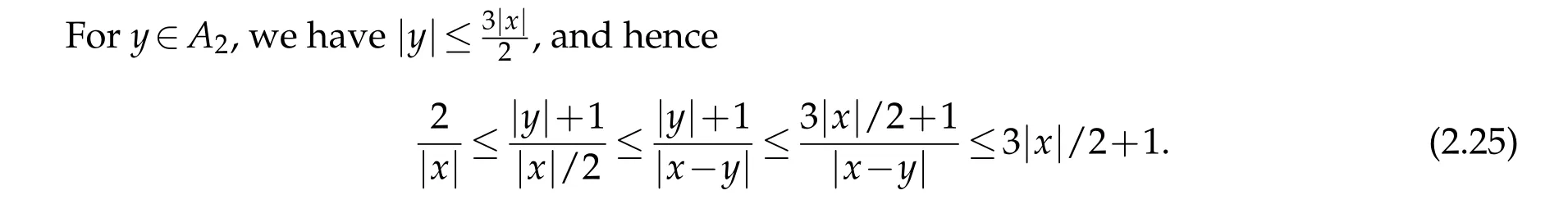
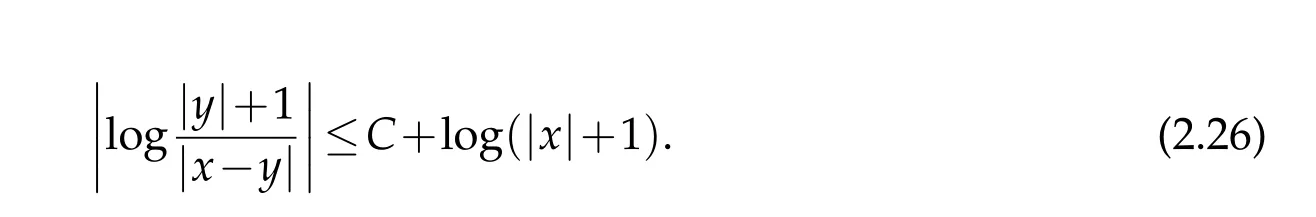
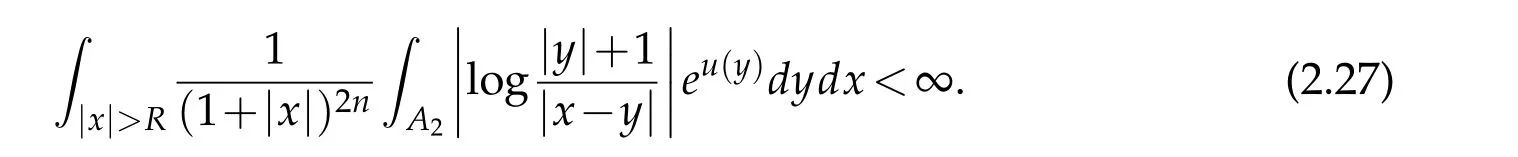


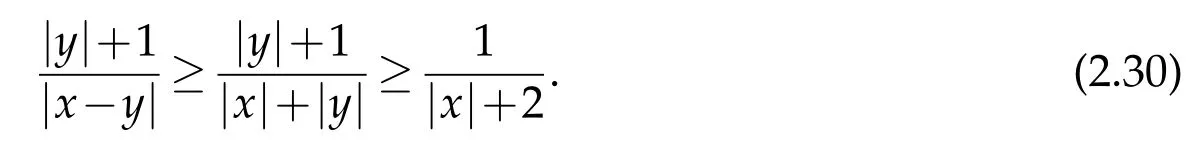
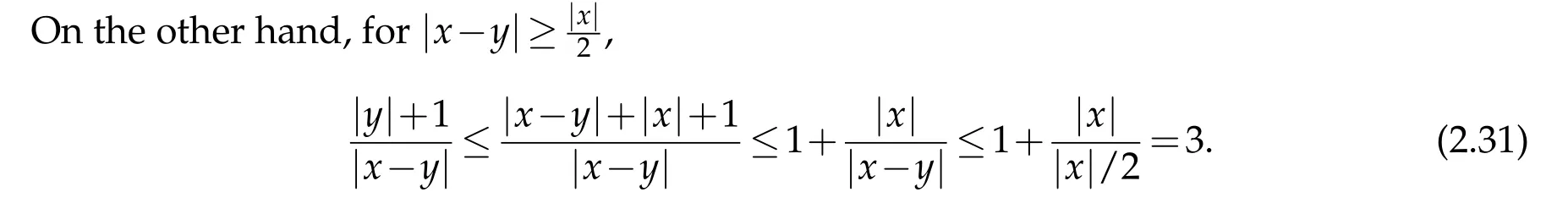
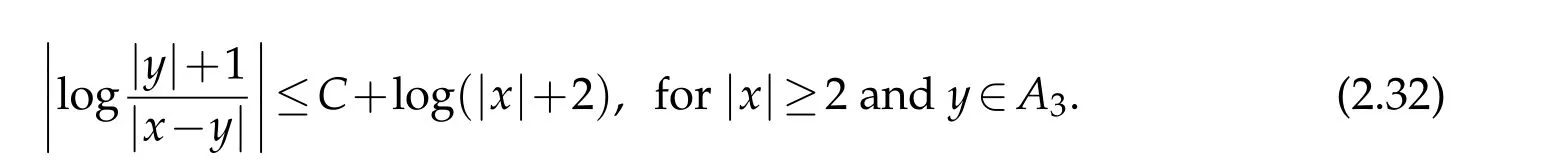
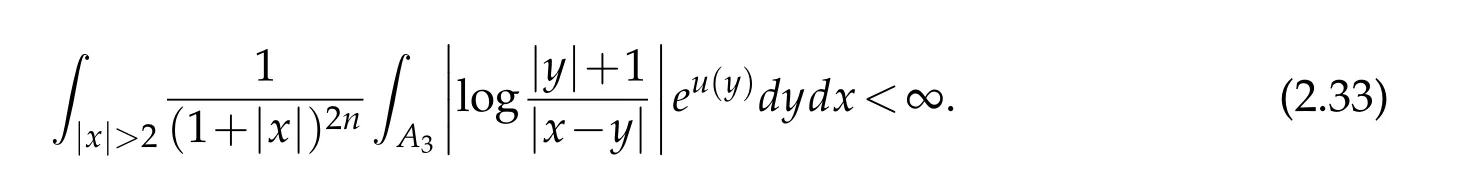


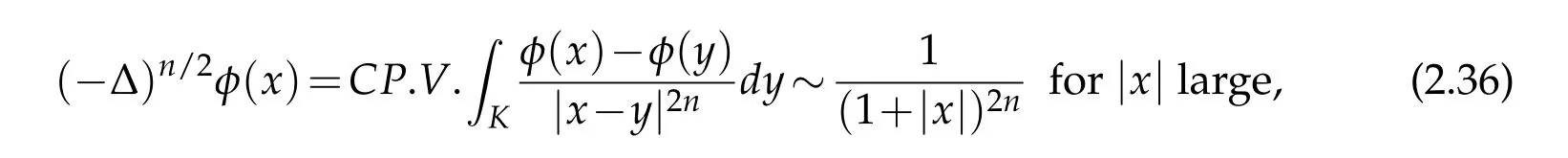

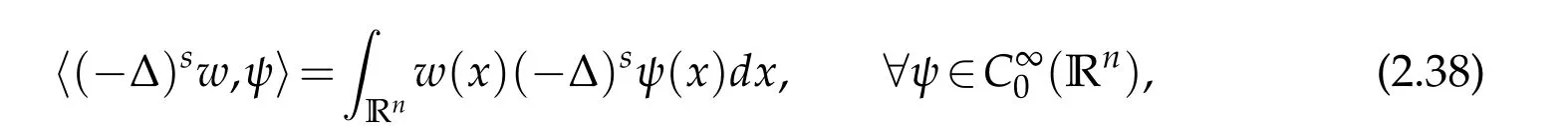
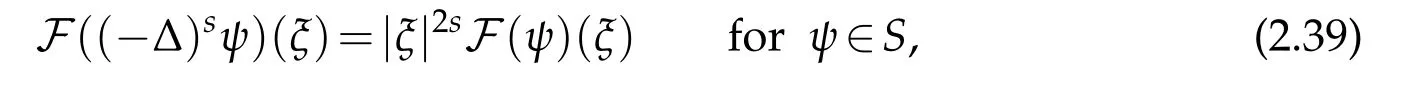
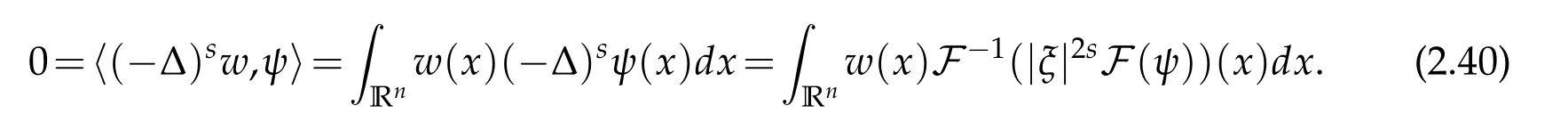

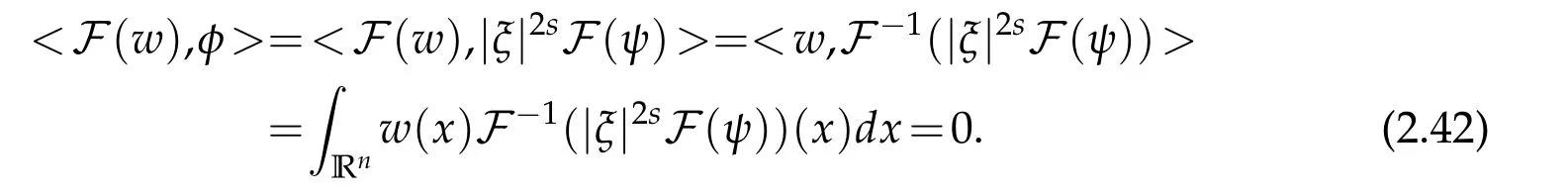





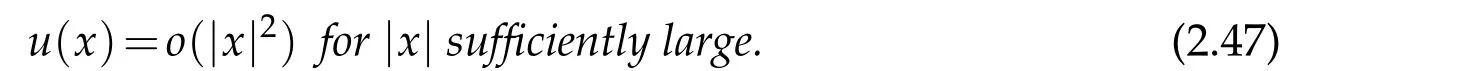



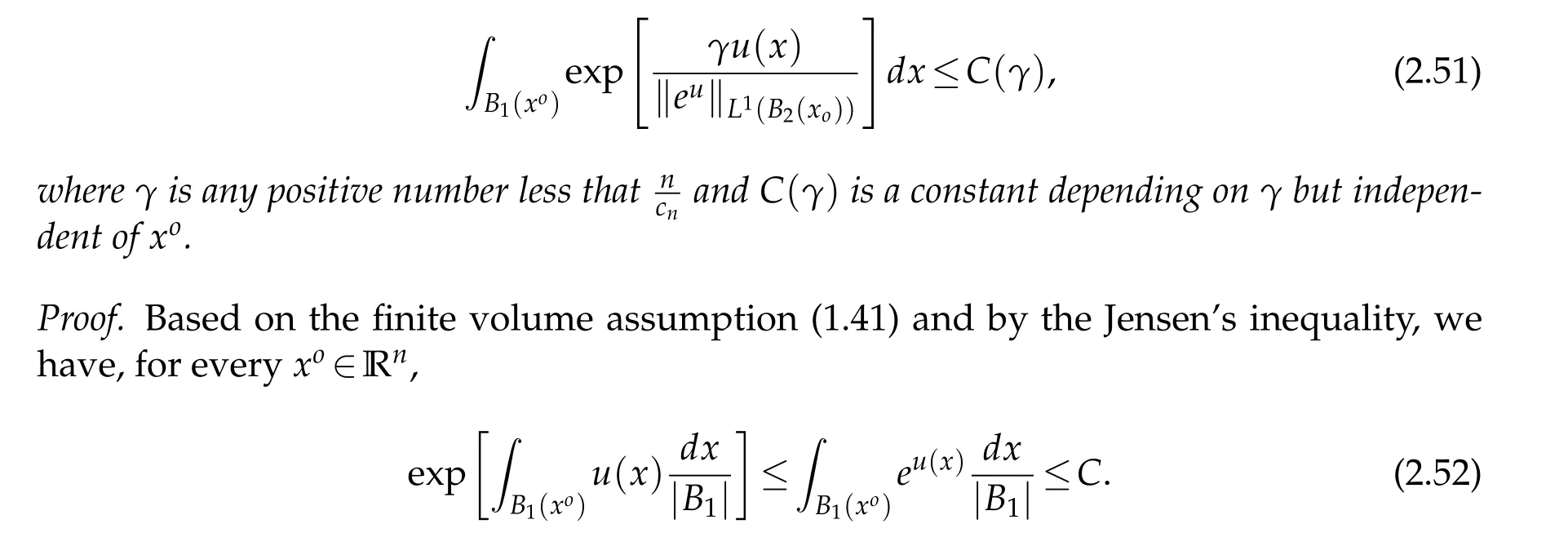
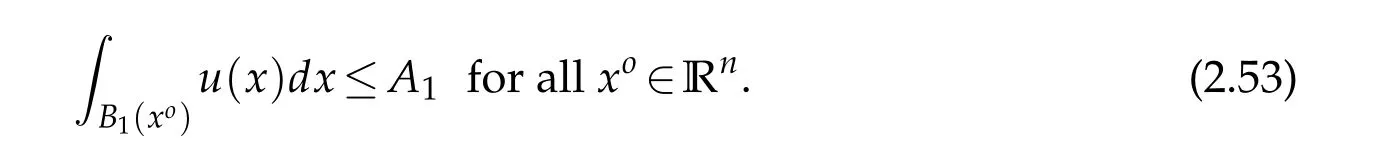

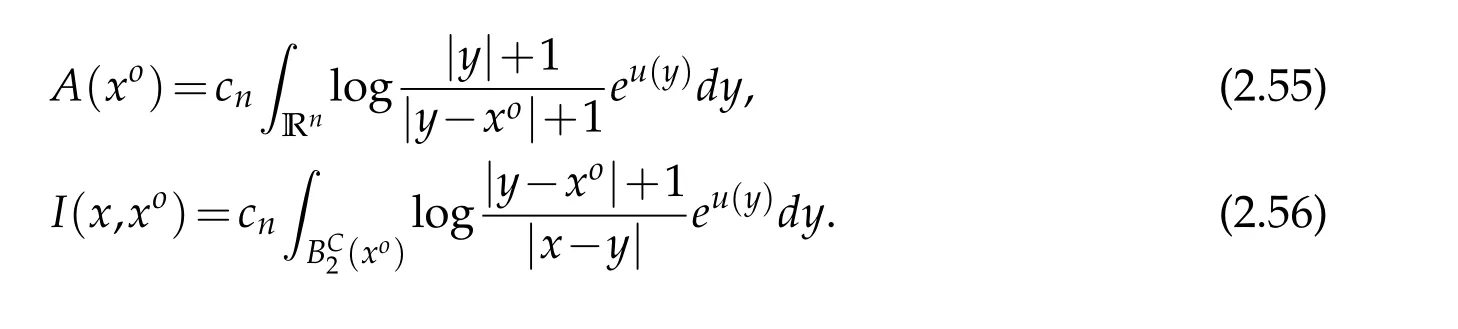
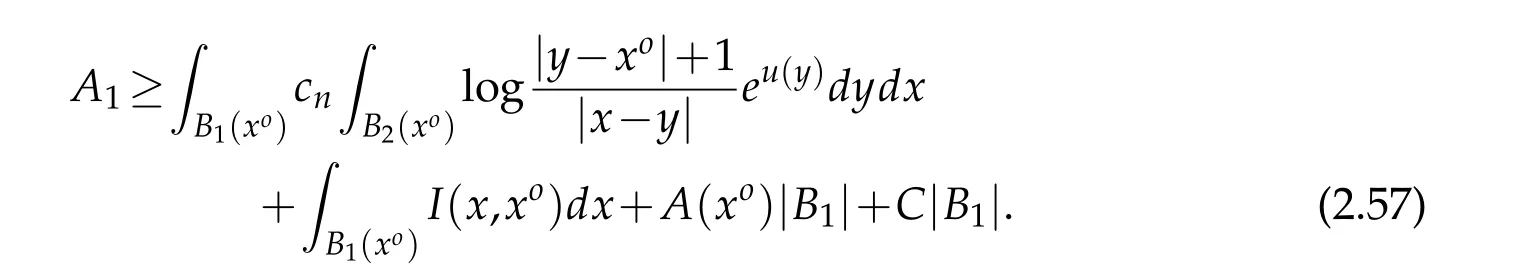
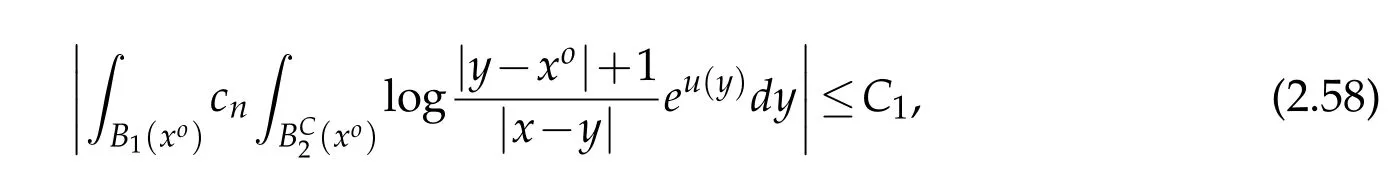

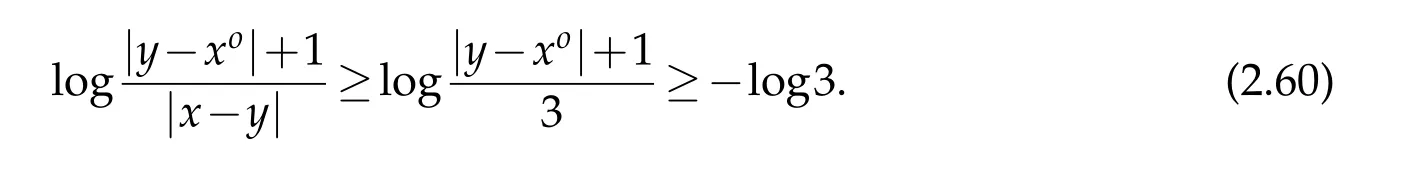

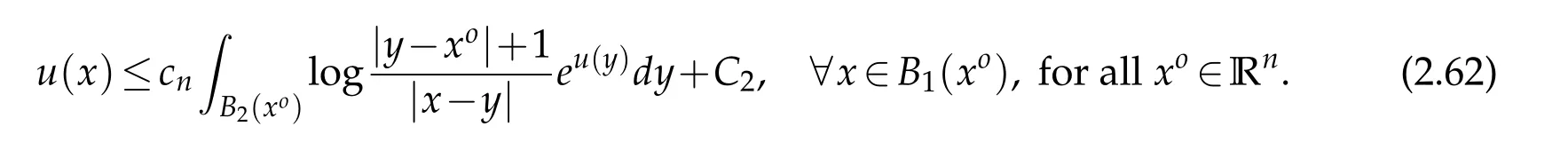

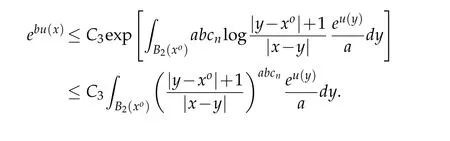
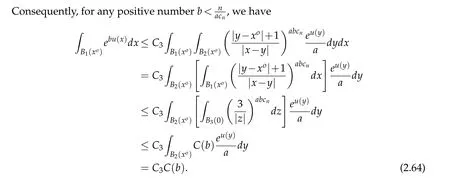
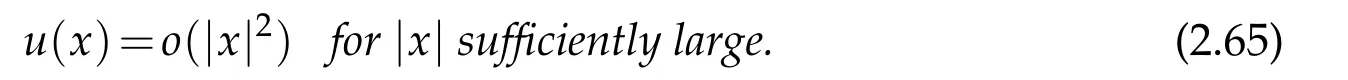





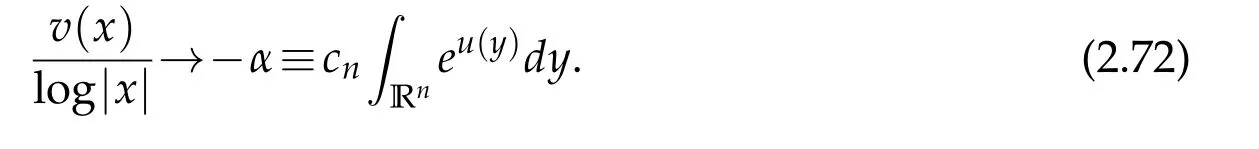

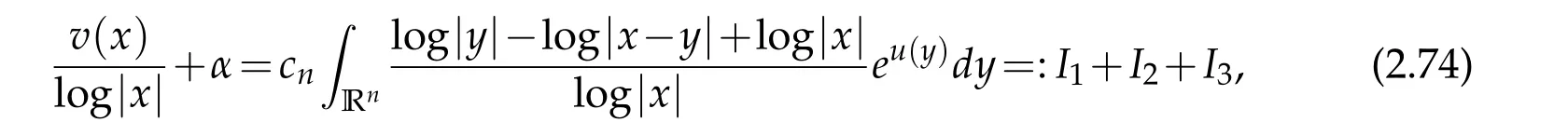
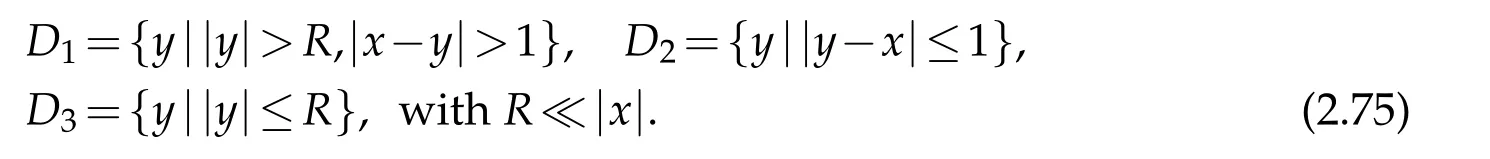
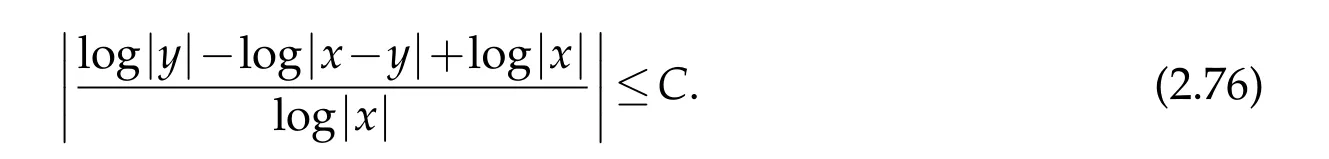
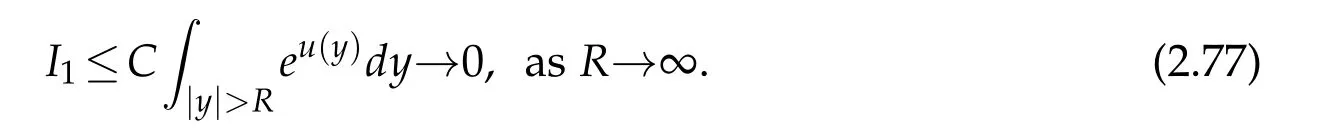
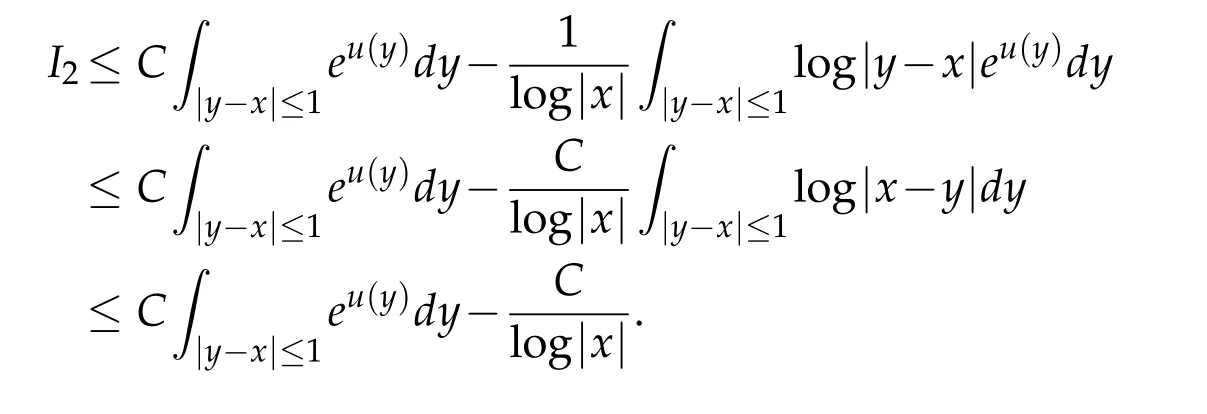

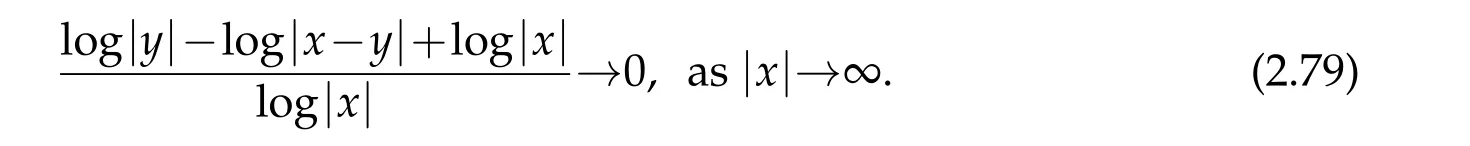


3 Classification of solutions in the case u(x)=o(|x|2)
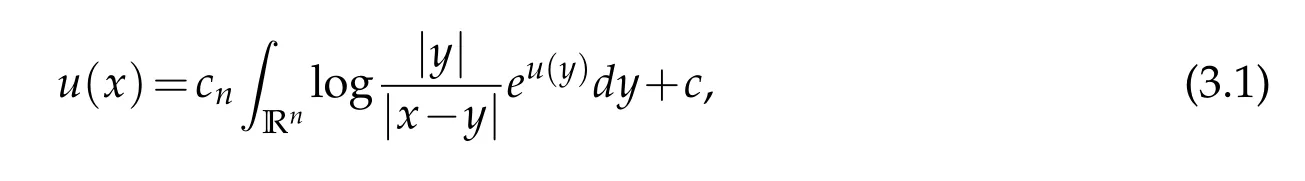

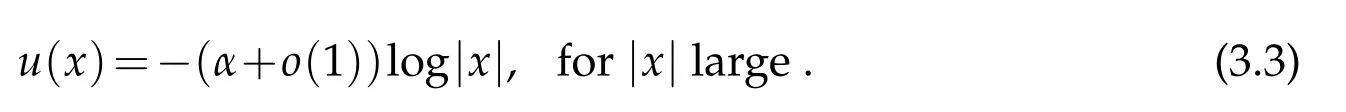

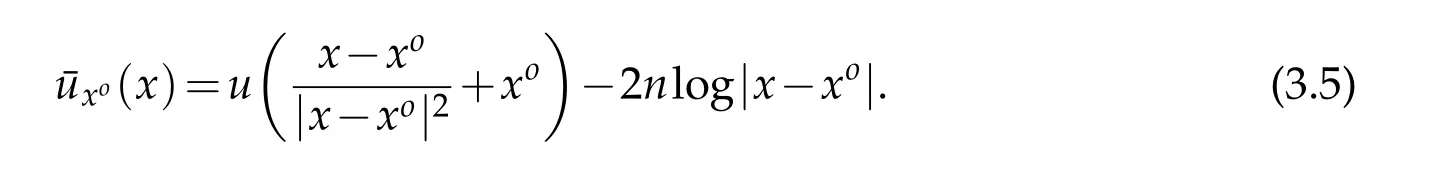
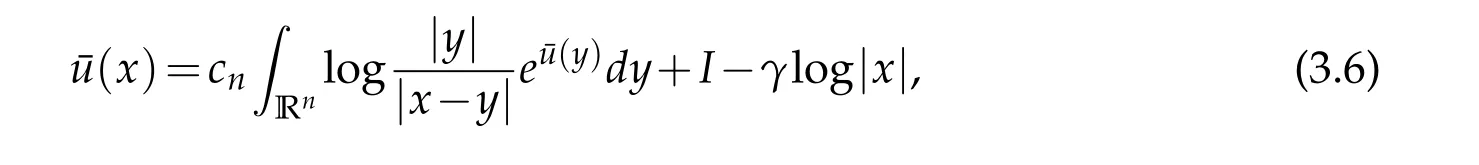

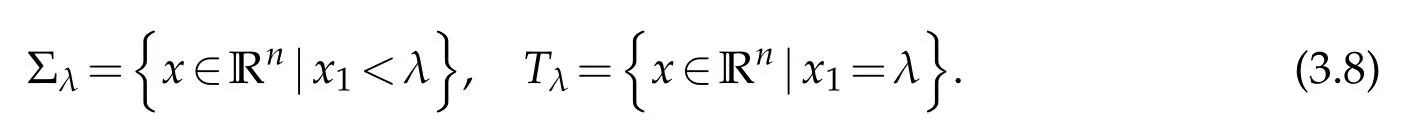
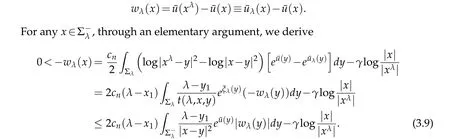
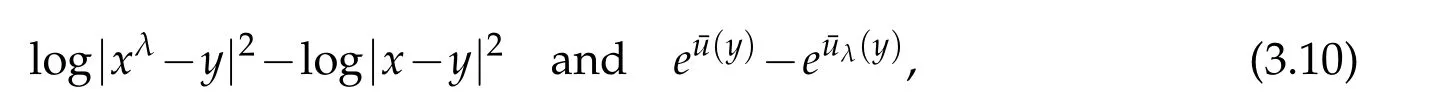

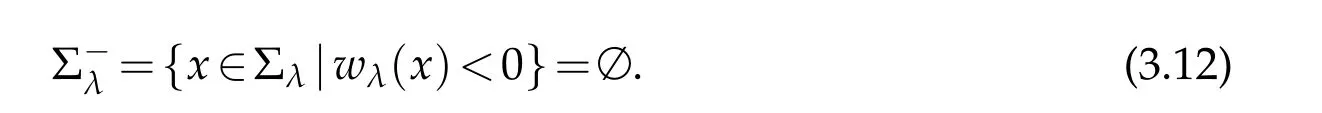
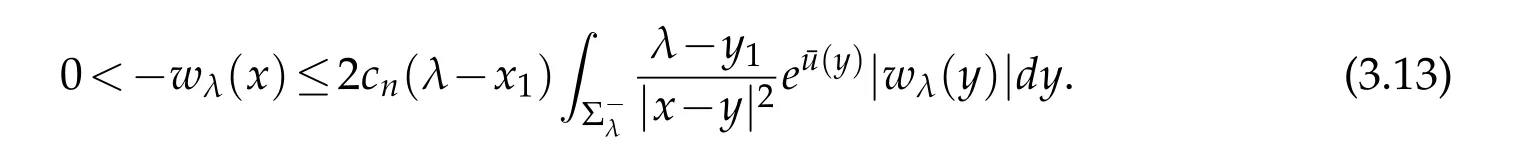

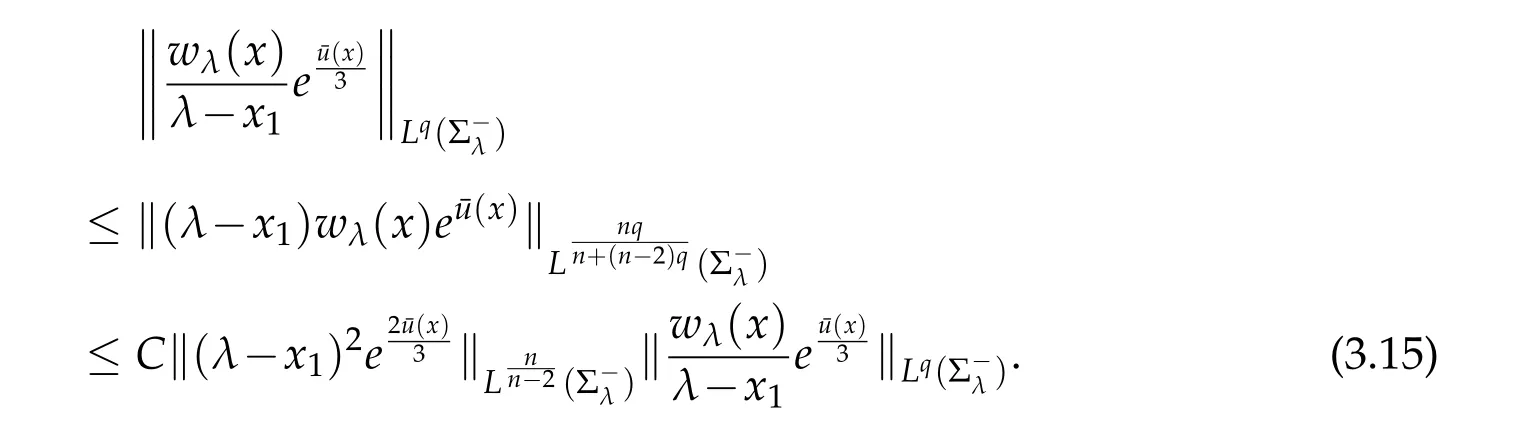

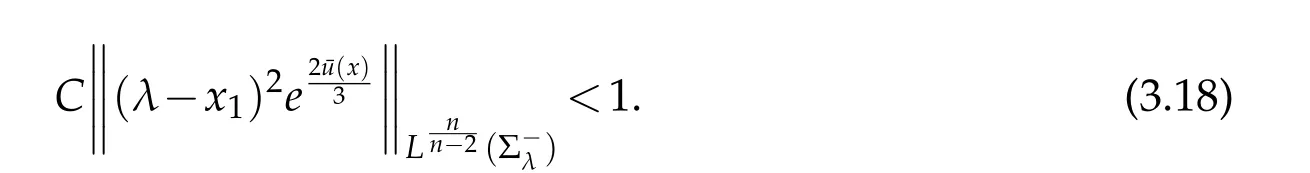
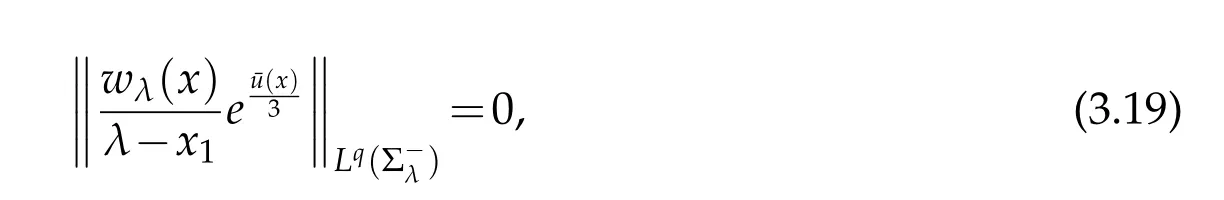

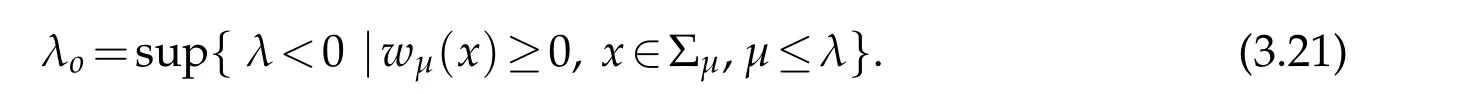
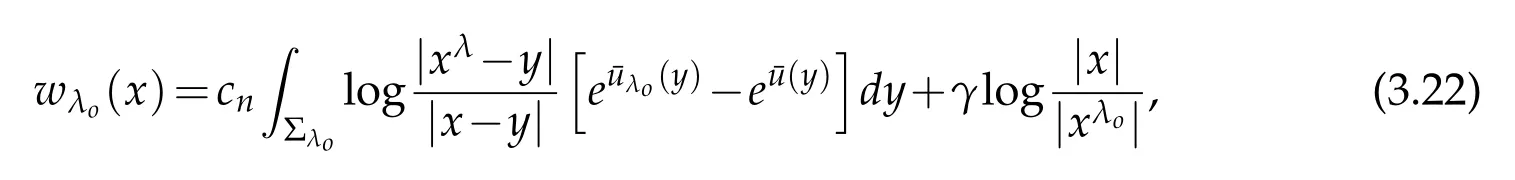

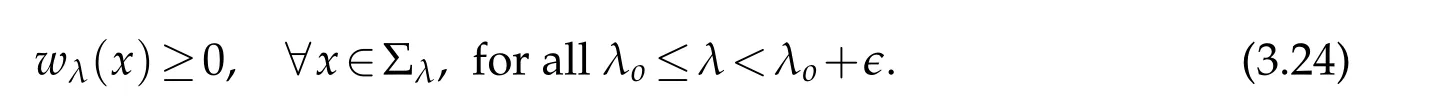



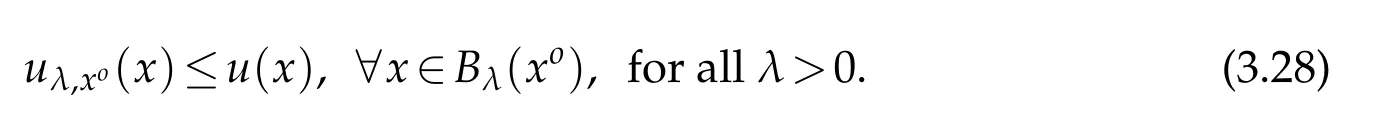

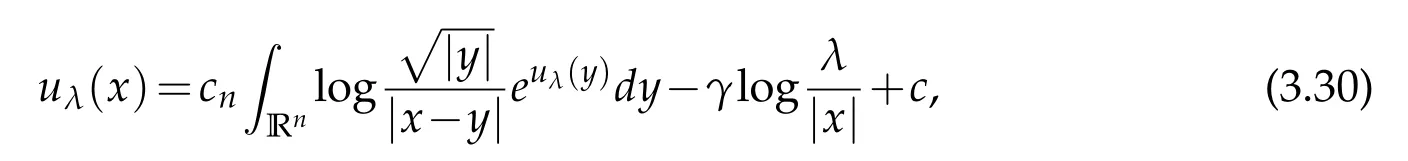
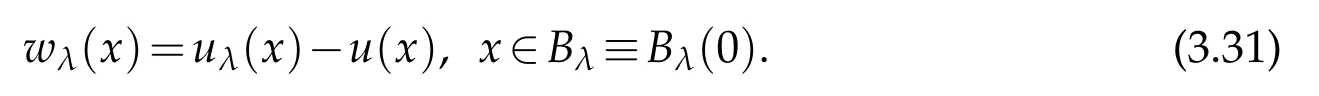
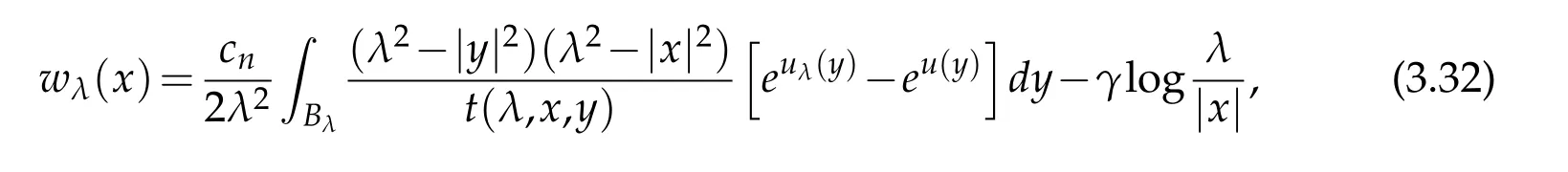
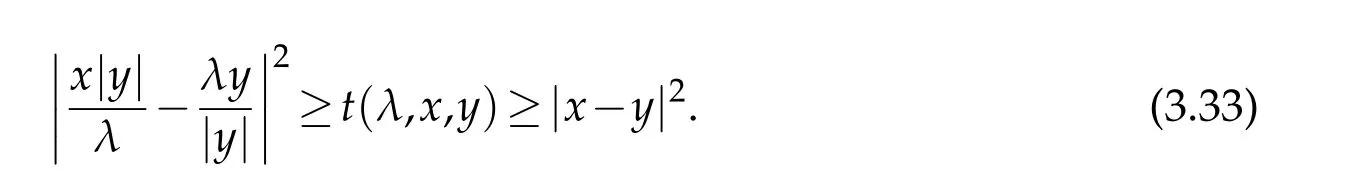


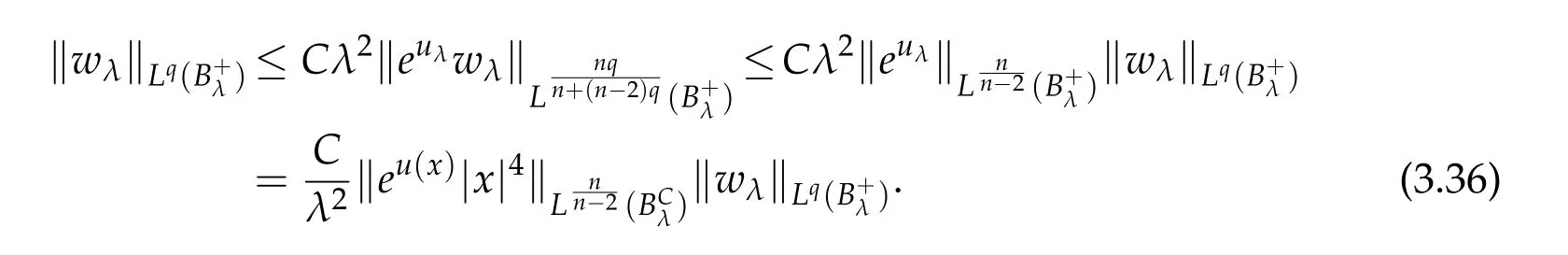

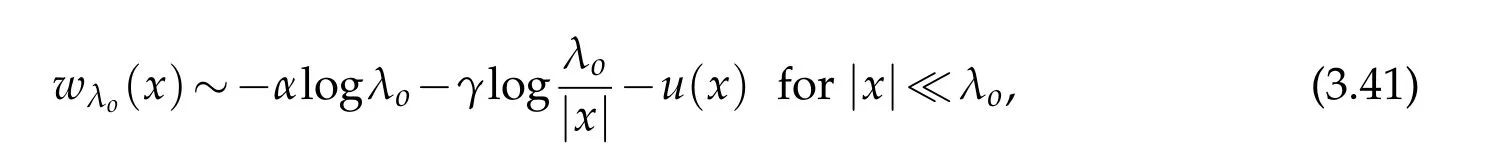

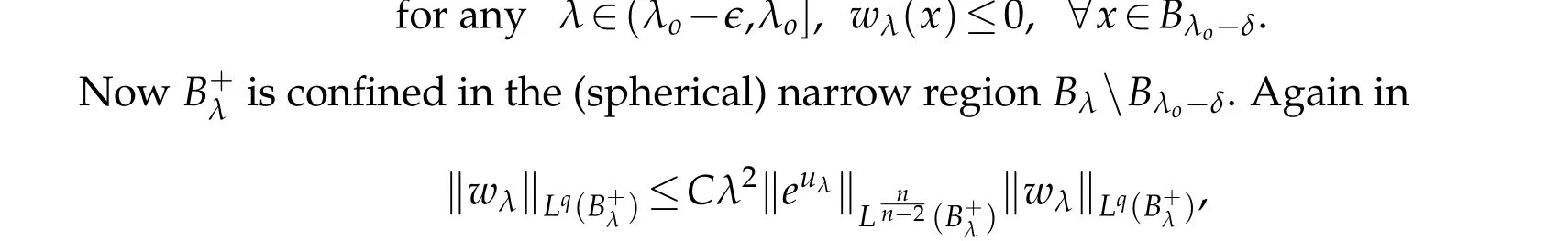




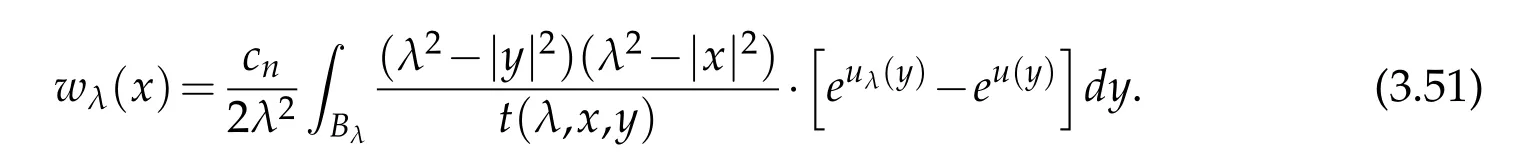


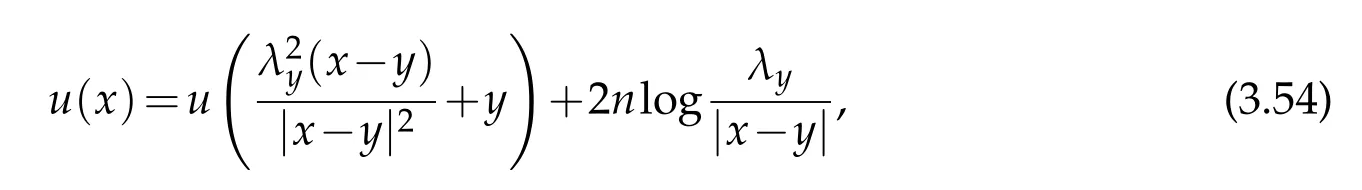

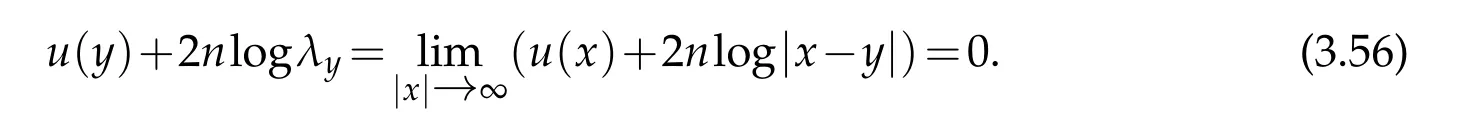

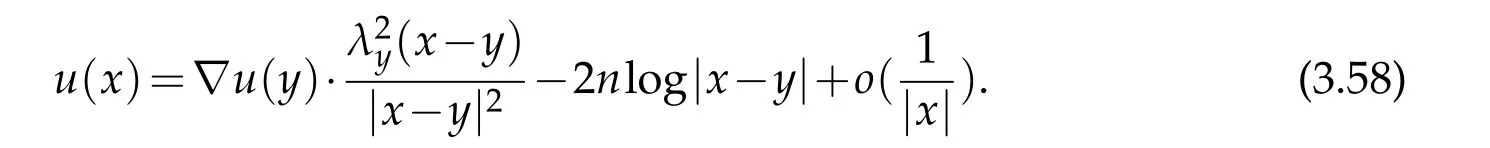
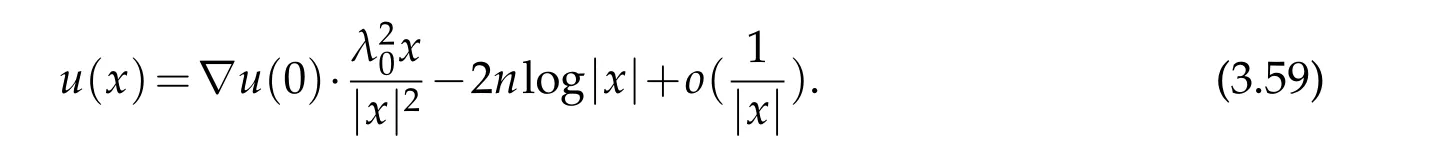
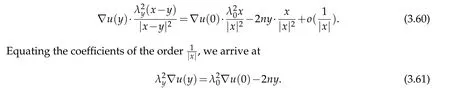




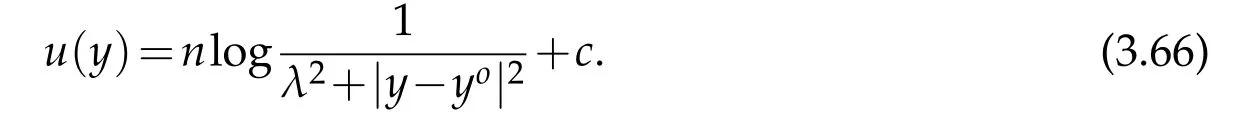

4 Symmetry of solutions in the case o(|x|3)