电磁轨道炮电枢装填推力影响因素分析

李明涛，曹 斌，葛 霞，裴朋超，国 伟

(西北机电工程研究所，陕西 咸阳 712099)

在固体电枢设计过程中，电枢尾翼跨距往往被要求比电磁轨道炮正负两轨之间的距离要大一些，这个大的量值往往称为过盈量。通常固体电枢采用铝合金制作，而正负轨道采用铜合金制作[1-2]。当固体电枢被推入电磁轨道炮内膛时，固体电枢由于材质较软，而轨道材质较硬且位置被严格约束，电枢尾翼的跨距会失去“过盈量”。固体电枢失去的“过盈量”会在电枢内部储存一定的弹性能，使得电枢尾翼外表面紧紧的压接在内膛轨道表面，并保持着一定的机械压力。这种机械压力会抵抗发射初始时刻因为电磁力导致电枢尾翼表面与轨道表面分离的趋势，从而保证电枢与轨道通电时仍具有足够的接触面积。

在以往的电磁轨道炮供输弹装置设计中，设备的输出推力通常选用电枢过盈量产生的预压力与枢-轨两种材料间的摩擦因子乘积的2倍值作为基准，但是在已经做过的电磁发射试验中发现，设备实际输出推力要比这个基准值大很多，在某些情况下甚至会超过设备的功率上限。

在已发表的许多论文中，很多专家学者已经就电枢材料[1-2]、电枢结构形式[3-6]、轨道材料、轨道结构形式[7]等进行了研究，并分析了电枢通流时的电流分布[8-9]、电枢的应力应变[10-11]。这些研究显示，一个设计良好的电枢通常具有以下结构特点：电枢在入膛后会被压缩，但是仍处于材料的弹性范围内[1-5]；电枢与轨道间的接触范围从电枢尾翼远端开始[12-13]。基于以上研究，笔者将建立一个符合这些结构特性的电枢-轨道模型，并利用NX 10.0软件的高级仿真功能，模拟推杆推动电枢入膛过程，分析电枢的应力应变、电枢-轨道接触压力，找出影响推杆推力变化的多种因素。

1 模型的建立

1.1 物理模型

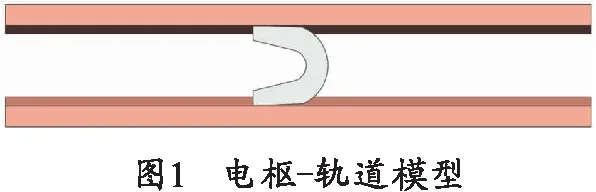
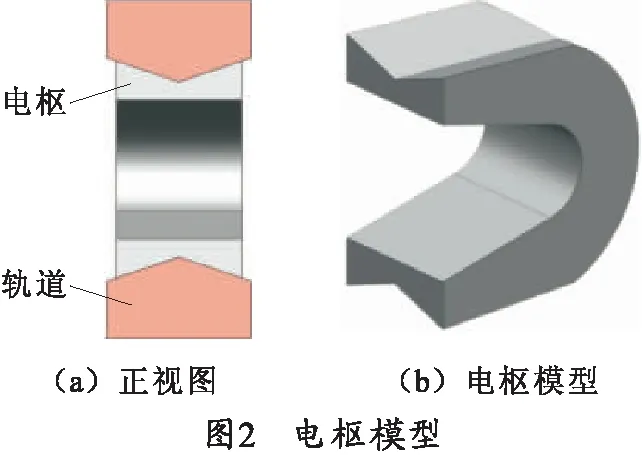
根据研究问题的需要，建立了如图1所示的电枢-轨道模型，与常规的平轨、凹凸曲面[4]截面形式不同，模型中轨道采用了凸三角形的截面形式，相应的电枢采用了常见的C-shaped形状，并对电枢两翼表面进行了凹向三角修改。电枢形状如图2所示。当电枢沿着轨道方向移动时，这种截面形式的电枢-轨道模型可以充分表达因推弹因素影响造成电枢上下、左右翻转时电枢-导轨接触性能变化。电枢-轨道模型配合依据“每安培一克”法则[2]设计了合适的过盈量，即电枢尾翼跨距比两个轨道之间的距离要大一些。

1.2 模型的初步分析

为了保证所建立的电枢-轨道模型具备良好的设计特征，对所建立的模型进行了初步有限元仿真分析。分析时应用 NX 10.0高级仿真模块中的NX NASTRAN解算器，并采用了ADVNL 601,106求解方案。ADVNL 601,106求解方案适用于高级非线性静态环境，这与电枢-轨道接触的情况非常匹配。分析前确定了电枢和轨道的材料强度特性，并按软件要求采用了材料指数塑性变形模型和电枢-轨道接触面摩擦因数。电枢和轨道材料强度特性如表1所示。

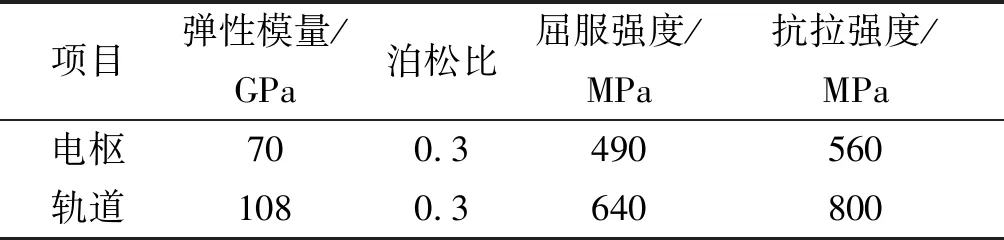
表1 电枢和轨道材料强度特性

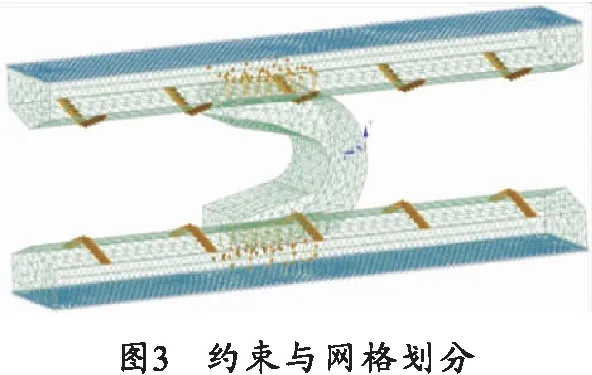
模型的有限元网格划分、模型约束与接触面设置如图3所示，枢-轨接触状态解算结果如图4所示，电枢应力水平如图5所示。

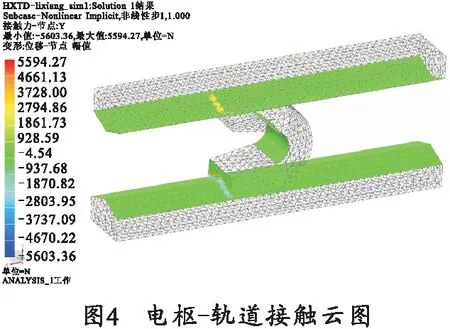
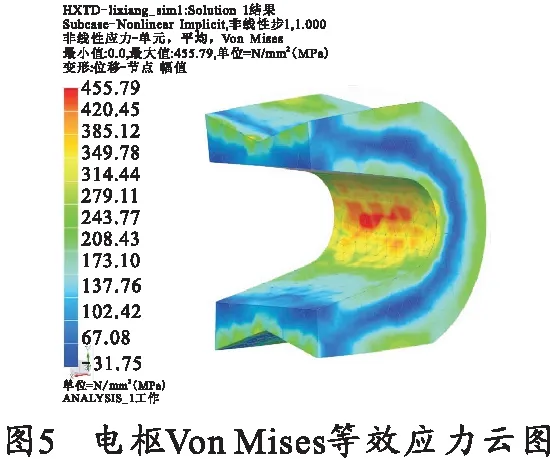
从图5可以看出，电枢与轨道的最大Von Mises等效应力为455.79 MPa，比设置的轨道和电枢材料屈服强度小很多，而如图4所示电枢与轨道的接触区域位于电枢尾翼远端，因此可以认为电枢正确装入轨道后电枢始终保持弹性变形，模型满足：电枢轨道结构变形处于弹性范围，电枢与轨道接触面处于电枢两翼尾端，这两个显著的结构特点。

2 电枢颈部推弹过程分析

2.1 颈部推弹过程分析

在以往的试验中，经常采用如图6所示的推弹装填方式将电枢推入发射器内膛中，这种方式所采用的推弹杆前端通常设计有与电枢内侧圆弧相似的外圆弧，以保证推杆向前运动过程中推杆前端与电枢内圆弧之间保持良好的接触。推杆的动力来源通常有人力装填方式、液压缸推动方式以及电动缸推动方式，由于制造、装配等因素的影响，电枢运动过程中推杆很可能发生偏转或偏移。除此以外，在发射器制造过程中，上下轨道之间可能存在一定的不对称性，轨间距与设计的存在不一致等，这些因素都有可能造成推杆装填推力的变化。为此，在后面的电枢颈部推弹过程分析中，分析了推杆左右偏移，上下偏移，推杆沿前端圆弧面中心发生偏转，以及上下轨道存在错位等条件下的电枢装填力。

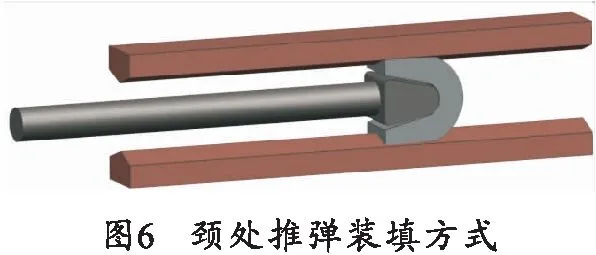
为了减少计算时间，建模时推弹杆只采用了前端部分结构，如图7所示。

仿真初始时刻，推弹杆与电枢之间设置间隙，首先按照电枢与轨道的过盈量设置计算两者接触后的力学状态，随后采用位置约束设置推弹杆后端面位置，令推杆与已被轨道压缩的电枢接触并一起向前运动。当计算完成时，就可以从推杆后端面网格节点上提取反作用力，这个反作用力的合力即为推动电枢运动时的装填力。推弹杆材质为常用steel，有限元计算的过程与前面“模型的初步分析”类似。

2.2 装填过程计算

装填过程分析时，首先利用NX 10.0软件对多种条件下的推杆-电枢-轨道模型进行三维建模，然后调用高级仿真功能对模型进行有限元分析。

有限元分析时，利用NX NASTRAN解算器和ADVNL 601,106求解方案，对装填过程进行准静态的计算。具体操作中，首先对上下轨道背面进行了固定约束，并将电枢与轨道之间接触设置为相同的摩擦因数，且推头仅允许前后滑动，然后在推头后端面逐步施加向前的推力，推力值初始设置为0～2.6 kN.当推力小于摩擦力时，整个模型处于静止平衡态，求解器可以正常求解；但是当推力大于摩擦力时，电枢会发生滑移，模型处于不平衡态，求解器会因为无法收敛而停止计算。因此，结构失稳前的最后一组解算数据最接近电枢入膛的最小推动力，以该组数据下的电枢-轨道等效应力以及推杆反作用力作为下面分析比较的基础。

2.2.1 理想情况

理想情况下装填过程应力云图如图8所示，推杆节点反作用力如图9所示，可以看出电枢最大Von Mises等效应力为439.47 MPa，推杆节点反作用力合力为18.262 kN.

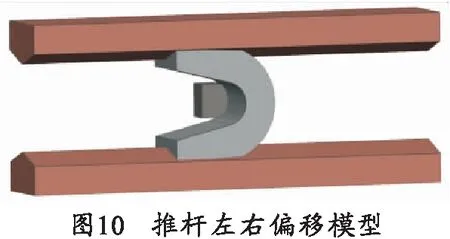
2.2.2 推杆左侧1/4接触时

推杆左右偏移模型如图10所示，通过仿真可知，推杆偏移3/4时，装填过程中电枢最大Von Mises等效应力为450.63 MPa，推杆节点反作用力合力为18.265 kN.

2.2.3 推杆上下偏移轨间距的2%时

推杆上下偏移模型如图11所示。通过仿真可知，推杆上下偏移轨间距的2%时，装填过程中电枢最大Von Mises等效应力为481.20 MPa，推杆节点反作用力合力为23.241 kN.

2.2.4 推杆偏转2°时

推杆偏转模型如图12所示。通过仿真可知，推杆偏转2°时，装填过程中电枢最大Von Mises等效应力为439.73 MPa，推杆节点反作用力合力为18.246 kN.

2.2.5 轨道左右错位电枢宽度的2%时

上、下轨道左右错位模型如图13所示。通过仿真可知，轨道左右错位电枢宽度的2%时，装填过程中电枢最大Von Mises等效应力为441.98 MPa，推杆节点反作用力合力为18.202 kN.

3 电枢尾部推弹过程分析

3.1 尾部推弹过程分析

在一些试验中，有时也会采用如图14所示的装填杆将电枢推入发射器内膛中。这种方式所采用的推弹杆前端通常设计为长方体，长方体前端面与电枢两个尾翼的端面接触推动电枢入膛。推杆的动力来源通常也有人力装填方式、液压缸推动方式以及电动缸推动方式，由于制造、装配等因素的影响，在推动电枢运动过程中推杆前端面也很可能只有一部分与电枢接触，造成推杆装填推力的变化。

3.2 装填过程计算

3.2.1 理想情况

为了分析这些因素对装填力的影响，建立相应的理想模型，如图15所示。

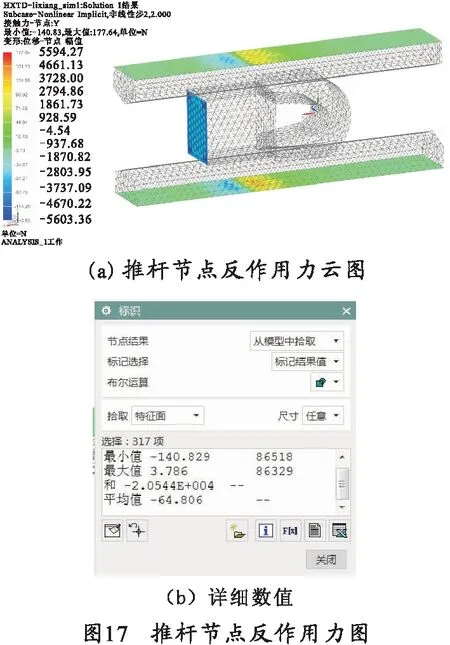
理想情况下装填过程应力云图如图16所示，推杆节点反作用力如图17所示，可以看出最大Von Mises等效应力为450.75 MPa，推杆节点反作用力合力为20.544 kN.

3.2.2 推杆左侧1/4接触时装填过程计算

推杆左右部分接触模型如图18所示。通过仿真与计算，得知推杆左侧1/4接触时电枢最大Von Mises等效应力为484.36 MPa，推杆节点反作用力合力为24.761 kN.

3.2.3 推杆上侧接触时装填过程计算

然后，运用考虑环境负产出的动态EBM-MI指数来测算中国各工业行业的低碳全要素生产率，且期到期的动态Malmquist指数的具体表达式如下：

推杆上侧接触模型如图19所示。通过仿真与计算，得知推杆上侧接触时电枢最大Von Mises等效应力为494.71 MPa，推杆节点反作用力合力为23.751 kN.

4 结果分析

将上面所建模型的有限元计算电枢入膛时的条件、应力以及装填力(节点反作用力)汇入表2中。从表2中可知：

1)理想条件下，不论是电枢颈部推弹还是电枢尾部推弹，推杆过程中的电枢最大等效应力都会比电枢入膛后只被轨道约束时的最大等效应力(455.79 MPa)要降低一些，其中电枢颈部推弹时应力降低的更多。

2)当推杆条件与理想情况发生偏差时，电枢最大等效应力均会有所增加。对于电枢颈部推弹来说，推杆发生上下偏移时应力水平上升显著(大于5%)；而对于推杆左右偏移、角度偏转、轨道位错等情况，电枢应力水平变化不大。对于电枢尾部推弹，不论是推杆左右偏移，还是上下单侧接触，都会带来电枢应力水平的显著上升。

3)理想条件下，电枢颈部推弹比电枢尾部推弹所用装填推力要小很多(12.5%).对于电枢颈部推弹来说，当推杆上下偏移时，电枢装填力显著上升(27.2%)，其他情况时则变化不大。对于电枢尾部推弹，不论是推杆左右偏移，还是上下单侧接触，都会带来电枢装填力的显著上升。

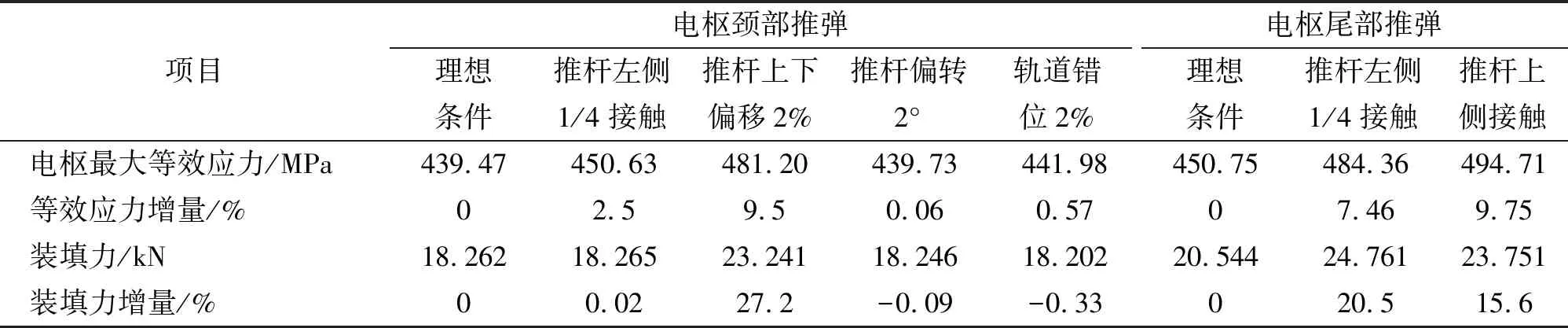
表2 不同装填条件下的装填状态表

5 结束语

电磁轨道炮电枢入膛时的装填推力大小直接决定着装填系统的功率、质量等总体参数，因此最大程度的降低装填推力需求是实现装填系统轻量化、小型化的关键环节，有着重要的军事应用价值。

笔者通过设计合理的仿真模型，将影响推力的电学因素予以剔除，只关注推杆与电枢的相对形位关系对推力的影响。从计算结果可以看出：一是电枢颈部推弹要优于电枢尾部推弹；二是推杆上下偏移最容易造成推弹力的上升。

实际上,装填电枢时造成设备输出功率上升的因素，除了电枢-推杆的前端因素，还有长悬臂梁式推弹方式造成设备自身损耗上升的后端因素，如何控制这些因素，降低损耗是今后研究的方向。