三阶半线性中立型时滞微分方程的振动性①
2020-03-19林靖杰曾伟宏李丹
林靖杰,曾伟宏,李丹
(广东石油化工学院 理学院,广东 茂名 525000)
1 引言
考虑如下的一类三阶半线性中立型时滞微分方程
[r(t)|Z″(t)|α-1Z″(t)]+q(t)|x(σ(t))|β-1x(σ(t))=0,0 (1) 的振动性,其中Z(t)=x(t)+p(t)x(τ(t)),β>0,α>0,α,β为两个正奇整数之比。 假设下列条件成立 (A1)p(t),q(t)∈C([t0,∞),(0,∞)),0≤p(t)≤p<1,q(t)>0; (A3)τ(t),σ(t)∈C1([t0,∞),(0,∞)),对任意t≥t0,都有 如果x(t)有任意大的零点,则式(1)的解称为振动的,否则称其为非振动的;若式(1)的所有解都是振动的,则称方程(1)是振动的,否则称其为非振动的[1]。 文献[2-4]对二阶半线性中立型微分方程 (r(t)|Z′(t)|α-1Z′(t))′+q(t)|x(σ(t))|β-1x(σ(t))=0 (2) 做了深入研究,给出一些新的振动准则。近年来,这一理论在应用数学领域中得到了迅速的发展及广泛的应用,如:金融经济、化学反应过程的稳定性的研究、飞机和导弹飞行的稳定性的研究、人口统计等问题。 定理1 假设条件(H1)-(H5)[14]及 成立,如果 定理2 假设条件(H1)-(H5)[14]及 成立,如果 文献[15]研究了式(1)在β>α情况下的振动性,得到的主要结果有: 定理3 若存在函数ρ∈C1([t0,∞),(0,∞)),满足A1(t)>0和 定理4 若存在函数ρ∈C1([t0,∞),(0,∞)),使 [r(t)|Z″(t)|α-1Z″(t)]′+q(t)|x(σ(t))|α-1x(σ(t))=0,0 (3) 新的振动性结果。它推广和改进了文献中的一些结果,并将举例说明主要结果的应用及其先进性。 引理1 若x(t)是式(1)的最终正解,则Z(t)只有下列两种可能,即存在T≥t0,使得当t≥T时,有(A)Z(t)>0,Z′(t)>0,Z″(t)>0;(B)Z(t)>0,Z′(t)<0,Z″(t)>0[4]. 引理3 设u(t)>0,u′(t)>0,u″(t)≤0,t≥t0,对任一θ∈(0,1) ,则存在Tθ≥t0,使得u(σ(t))≥ 引理4 设u(t)>0,u′(t)>0,u″(t)>0,u‴(t)≤0,t≥Tθ,则存在γ∈(0,1)和Tγ≥Tθ,使得u(t)≥ γtu′(t),t≥Tγ[6]. 为了方便,使用记号:对于ρ,σ∈C1([t0,∞),(0,∞)),设 定理5 若存在函数ρ∈C1([t0,∞),(0,∞)),满足A1(t)>0,且有 (4) 成立,则式(3)是振动的。 证明设式(3)有非振动解x(t),由于x(t)=0无实际意义,只考虑x(t)≠0的情形。设x(t)为式(3)的最终正解,且x(σ(t))>0,x(τ(t))>0,t0≤t1≤t. 由引理1可知,存在t2>t1,使当t≥t2时,Z(t)只有引理1中(A)与(B)两种可能。 当Z(t)满足引理1中(A)时,由于τ(t)≤t,故Z(t)≥Z(τ(t))且x(t)≤Z(t),进而有x(t)=Z(t)- p(t)x(τ(t))≥Z(t)-p(t)Z(τ(t))≥(1-p(t))Z(t)≥(1-p)Z(t)则 xα(σ(t))≥(1-p)αZ(σ(t))α (5) 因为Z″(t)>0,此时由式(3)和式(5)可得 (r(t)(Z″(t))α)′≤-q(t)(1-p)αZ(σ(t))α=-A2(t)Z(σ(t))α,t≥t2 (6) 考虑广义Riccati变换 (7) 对式(7)中t进行求导,并由式(6)得 (8) 由(A2)可知,r(t)≥0,r′(t)≥0,且(r(t)(Z″(t))α)′=r′(t)(Z″(t))α+αr(t)(Z″(t))α-1Z‴(t)≤0可得,Z‴(t)≤0. (9) 取T=max {t2,Tγ},由引理3可得,令u(t)=Z′(t),对任一θ∈(0,1),存在Tθ≥t0,使得 (10) 由引理4可得,存在γ∈(0,1)和Tγ≥Tθ,使得 Z(σ(t))≥γσ(t)Z′(σ(t)),t≥Tγ (11) 由式(9)~式(11)可得,此时式(8)为 (12) 当Z(t)满足引理1中(B)时,由于(r(t)(Z″(t)α)′≤0,且q(t)>0,1-ρ>0,Z′(t)<0,可得 (r(t)(Z″(t))α)′≤-q(t)(1-ρ)α(Z′(t))α=-A2(t)(Z′(t))α (13) 考虑广义Riccati变换 (14) 对式(14)中t求导,并利用式(13)的结果,可得 (15) V′(t)<-A2(t) (16) 令t→∞,根据式(4)可知,V(t2)→+∞,这与V(t)<0矛盾,故假设不成立,即当Z(t)满足引理1中(B)型时,x(t)是式(3)的振动解。 证毕。 定理6 若存在函数ρ∈C1([t0,∞),(0,∞))使得A1(s)>0,式(4)成立,且满足 (17) 则式(3)是振动的。 证明 设x(t)是式(3)的非振动解,如同定理5的证明,若Z(t)为引理1中(A)型,在这里,证明过程与定理5第一部分的证明过程一样。即当Z(t) 满足引理1中(A)型,x(t)是式(3)的振动解。 当Z(t)满足引理1中(B)型时,由于(r(t)(Z″(t))α)′≤0,则(r(t)(-Z″(t))α)′≥0,且q(t)>0,1-p>0,Z′(t)<0,可得 (r(t)(-Z″(t))α)′≥q(t)(1-p)α(Z′(t))α=A2(t)(Z′(t))α (18) 考虑广义Riccati变换 (19) 对式(19)中t求导,并利用式(18),可得 (20) 式(20)两边同时乘φα(t),并从t2到t进行积分,可得 (21) (22) 由于 (r(t)(Z″(t))α)′≤0,当s>t时,有r(s)(Z″(s))α≤r(t)(Z″(t))α,即 (23) 对式(23)两边从t到l(l>s)对s进行积分,可得 (24) 证毕。 推论若存在函数H(t,s)∈F和ρ∈C1([t0,∞),(0,∞)),使得式(4)成立,且 (25) 则式(3)是振动的。 注:(1)若取r(t)=1,p(t)=0,则式(3)即为文献[13]所研究的时滞微分方程,即定理5的结论推广了文献[13]的结果,应用更广泛;(2)若取β=α,式(3)就是文献[12]所研究的方程,因而定理5的结论改进了文献[12]的相应结果;(3)本文的研究结果改进了文献[14]相应的振动准则。 例 考虑如下的三阶中立型微分方程 (26) θ=1,γ∈(0,1).显然有 显然式(26)满足定理5的条件式(4),由此可知式(3)是振动的,而文献[12]的研究结论不能应用于此例。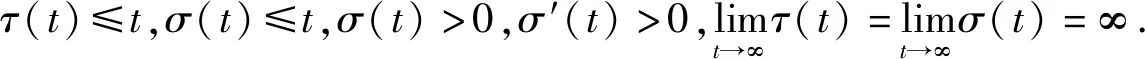
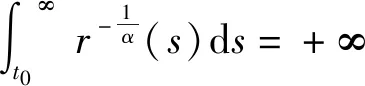
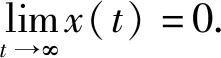
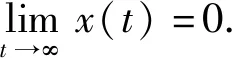
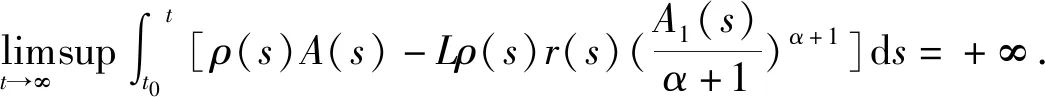
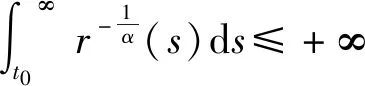
2 引理
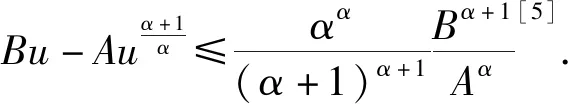
3 主要结果
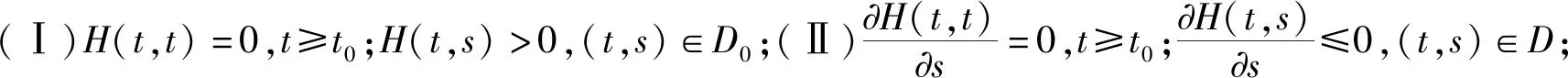
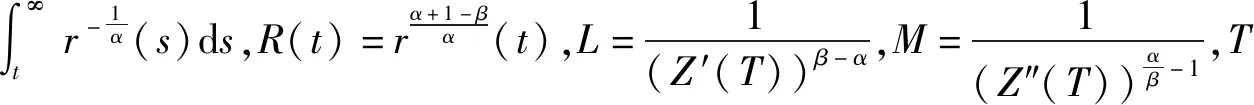
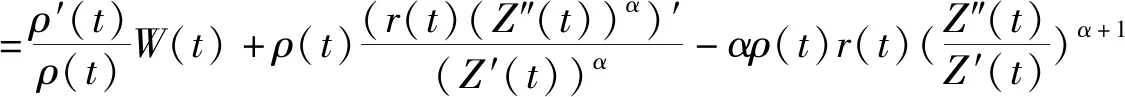
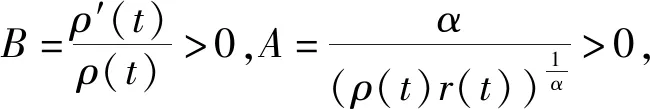
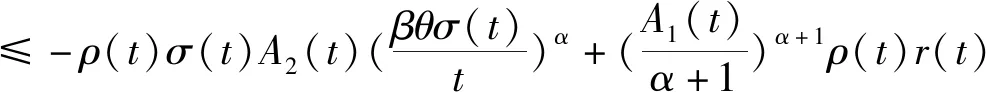
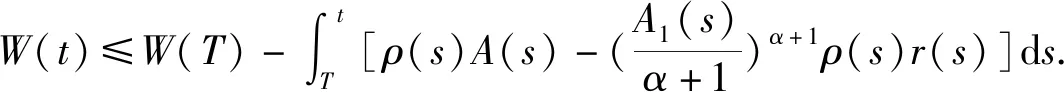
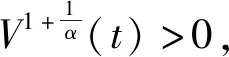
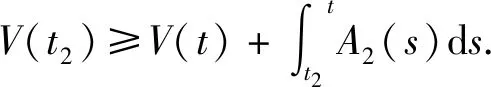
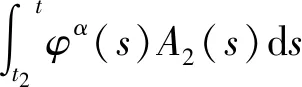
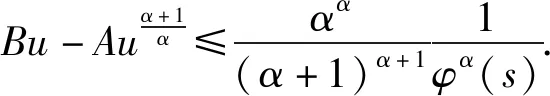
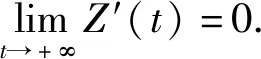
4 应用