硼化物基超高温复合陶瓷超高速撞击作用下破坏模式研究①

刘宝良，季杨，冯晓艳，程玲，赵春香，孙立红，乔牧

(1.广东石油化工学院 建筑工程学院，广东 茂名 525000；2.黑龙江科技大学 理学院，黑龙江 哈尔滨 150022)

当今的科学技术发展迅速，世界各国对太空领域的争夺也日益激烈，航天器是研究太空领域重要设备，所以发射卫星和航天飞机成了重中之重。然而空间碎片超高速撞击可能会损伤航天器关键部位，对航天器存在威胁，在此背景下，空间碎片撞击事件受到了广泛关注[1-3]。郭晓钧研究了脆性材料钻孔爆炸致裂机理[4]；黄雪刚等设计了以TiB2基陶瓷复合材料为缓冲屏的Whipple式防护构型并利用二级轻气炮在2.88～7.32 km/s的撞击速度范围内开展超高速撞击实验，对缓冲屏与典型全铝合金缓冲屏进行比较验证[5]；唐恩凌等对超高速撞击过程的能量分配进行了研究，对解决动能撞击、发展导弹拦截技术、判定空间飞行器被撞事件及评估碰撞破坏程度具有重要的理论意义[6]；曹智雄对空间粉尘高速撞击光学玻璃及PET等离子体和发光效应进行研究，分析了入射粒子参数对产生信号特征及其参数的影响规律[7]；冯晓伟以A95氧气铝陶瓷为主要研究对象，采用实验研究、理论分析和数值模拟相结合的手段系统地研究了陶瓷等脆性材料在冲击压缩下的波动过程以及破坏力学行为[8]；王洋采用二级轻气炮进行高速撞击，研究了不同撞击条件下M55J/AG-80复合材料的力学性能和撞击损伤区域的变化规律，及其损伤形式[9]。然而，采用理论模型开展超高速撞击研究非常困难，现阶段也仅针对某些物理量进行数值模拟和实验研究等工作。目前，主要是针对塑性材料开展超高速撞击研究，而对于脆性材料开展的研究较少。本文主要是针对超高温复合陶瓷脆性材料板进行超高速撞击研究。

1 理论模型的建立

在硼化物基超高温复合陶瓷靶板损伤模式分析研究中，弹丸高速撞击陶瓷靶板的破坏模式是复杂的，它使材料产生弹塑性变形，当弹丸产生的冲击波作用在靶板的表面时，靶板的内部产生各种应力波，使靶板产生许多裂纹，随着应力波的扰动和加强，裂纹也随之增长，靶板局部会分成许多个部分并且碎裂，最后形成穿孔，或者整体破坏。

在硼化物基超高温复合陶瓷材料高速撞击下损伤数值模拟中，采用圆柱形弹丸撞击靶板。将弹丸高速撞击靶板简化为均布冲击载荷对固定约束支撑板的作用，如图1所示，靶板长宽均为L0(40 mm)，冲击载荷的作用半径根据弹丸尺寸进行确定，当弹丸未破碎时，冲击载荷作用半径等于圆柱体半径，在冲击载荷作用下靶板单位面积上获得的瞬时冲量I0为[10]

I0=ρdV0

(1)

(2)

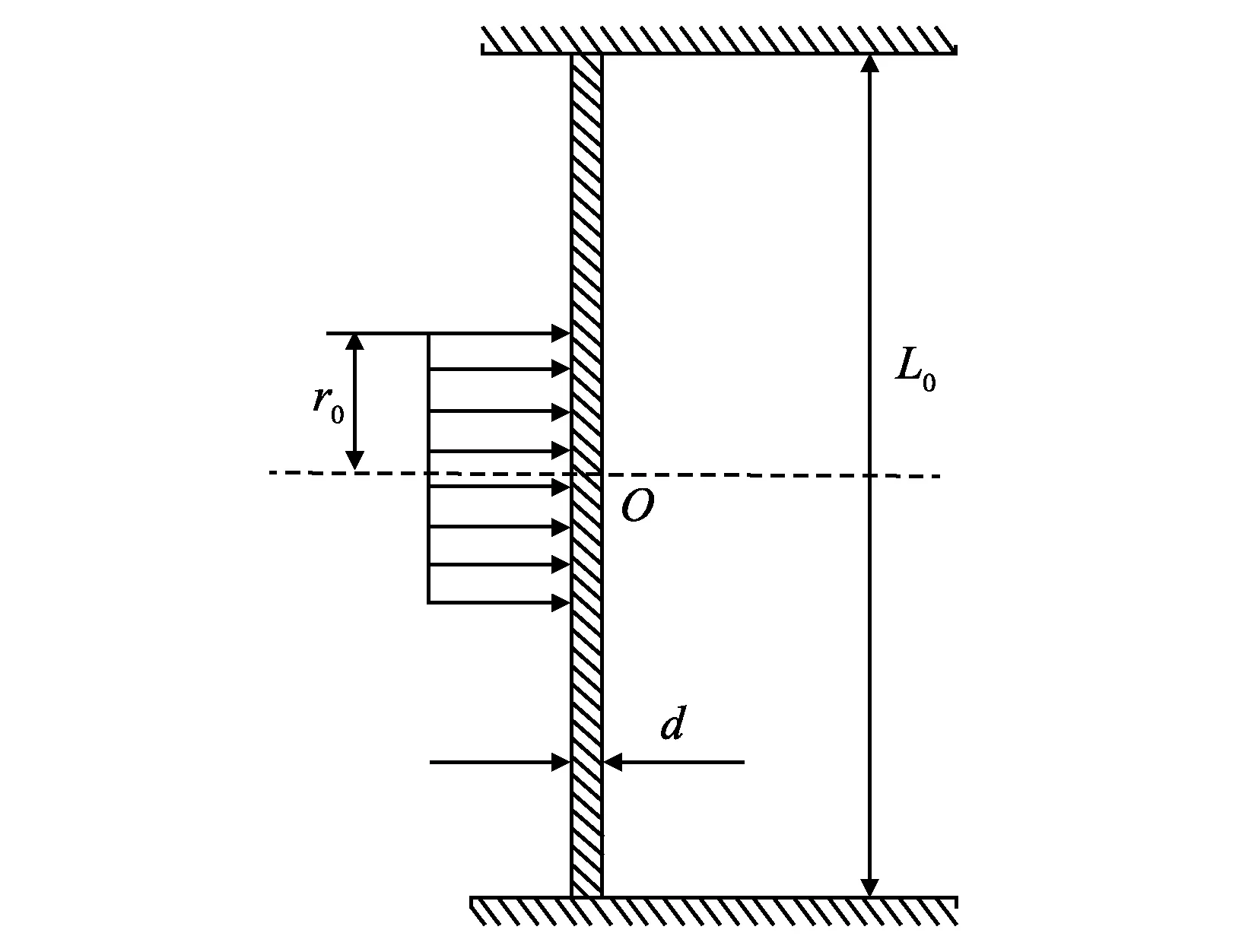
图1 弹丸冲击波对靶板作用简化模型

式中：ρ为靶板材料密度，kg/m3；d为靶板厚度，mm；V0为靶板在冲击载荷作用下获得的初速度，m/s；ms为弹丸质量，kg；νs为弹丸到达靶板时的速度，m/s；Is为气体冲击波对应的冲击载荷作用于靶板单位面积上的冲量，N·s；r0为冲击载荷的作用半径，mm。

靶板的主要损伤模式为中心穿孔和宏微观裂纹，并可以通过计算得到中心穿孔和裂纹的尺寸。为计算方便，将靶板的中心穿孔和裂纹等效为贯穿直裂纹，裂纹长度等于中心穿孔直径或孔周环形裂纹尺寸。碎片云及气体冲击波传递给靶板的能量E0主要转化为四个部分，分别为使靶板产生初始中心穿孔的能量Ecr、横向应变能Wx、纵向应变能Wy和孔周环形裂纹。其中E0可通过动能定理计算得：

(3)

根据最大塑性应变破坏准则，当靶板后表面产生的最大横向应变达到容器材料的极限应变εf，即(εr)max≥εf，在弹丸冲击波作用下靶板产生的最大横向应变为

(4)

式中：cv为材料的塑性波波速，m/s。

2 几何模型的建立

采用圆柱体厚弹丸正撞击边长为40 mm的正方形且有一定厚度的硼化物基超高温复合陶瓷板(ZrB2-30SiC)，然后用AUTODYN软件模拟弹丸在二级轻气炮下的撞击破坏模式。由于弹丸为高速运动状态且ZrB2-30SiC陶瓷板为脆性材料，所以弹丸高速撞击采用SPH法进行分析。弹丸和硼化物基超高温复合陶瓷靶板的建模采用的是二维轴对称方式，粒子数目为20个/mm2。

2.1 不同速度弹丸撞击靶板的破坏模式

表1 相同质量的弹丸在不同速度下撞击同一厚度靶板速度/(km/s)撞击一阶段撞击二阶段撞击三阶段135

在不同速度弹丸撞击靶板的破坏模式中,以速度为变量并且研究速度分别为1,3,5km/s,用半径为1mm,长度为3mm相同质量的圆柱型弹丸,撞击板厚为2mm的ZrB2-30SiC复合陶瓷板,其三个阶段的破坏情况见表1。

由表1可知,第一阶段弹丸由于压缩末端发生层裂出现扩张,最前端由于碰撞发生破碎,靶板由于冲击产生反溅碎片云,靶板被弹丸侵蚀。第二阶段弹丸末端发生剥落,弹丸由于速度不同基本完全破碎,弹丸完全穿过靶板产生穿孔。第三阶段弹丸完全破碎,穿孔直径基本不变,穿孔周围产生明显裂纹。因此，同一尺寸的弹丸，在同一厚度的靶板下，不同速度撞击，速度越大，穿孔半径亦越大。

2.2 不同质量弹丸撞击靶板的破坏模式

同类弹丸，尺寸改变弹丸质量也随之变化，半径为1 mm，长为3 mm的弹丸写为：1-3弹丸，以此类推。在不同质量弹丸撞击靶板的破坏模式中，分别选择0.5-1.0，1.0-2.0，1.5-3.0尺寸的圆柱形弹丸，于板厚过大，弹丸/板厚相差太过明显导致的。第三阶段弹丸完全破碎，穿孔直径基本不变，穿孔周围产生明显裂纹。因此，相同质量弹丸在相同的撞击速度下撞击不同厚度靶板的穿孔半径变化规律，靶板厚度越击靶板，弹丸穿透靶板。因此，靶板的击穿临界速度约为1.3 km/s(0.5-1.0弹丸)。以速度为3km/s,靶板厚度为2mm的ZrB2-30SiC复合陶瓷板,其三个阶段的破坏情况见表2。

由表2可知,第一阶段弹丸由于压缩末端发生层裂出现膨胀,碰撞0.5-1.0弹丸完全破碎,其他弹丸最前端发生破碎,靶板由于冲击产生反溅碎片,靶板被弹丸侵蚀。第二阶段弹丸由于质量不同破碎情况也不同,0.5-1.0弹丸至1.0-2.0弹丸完全破碎,其他大弹丸末端发生剥落,所有弹丸完全穿过靶板产生穿孔。第三阶段三种质量的弹丸完全破碎,穿孔直径基本不变,穿孔周围产生明显裂纹。因此,在同一撞击速度、靶板厚度相同的情况下,弹丸质量越大,穿孔半径亦越大。

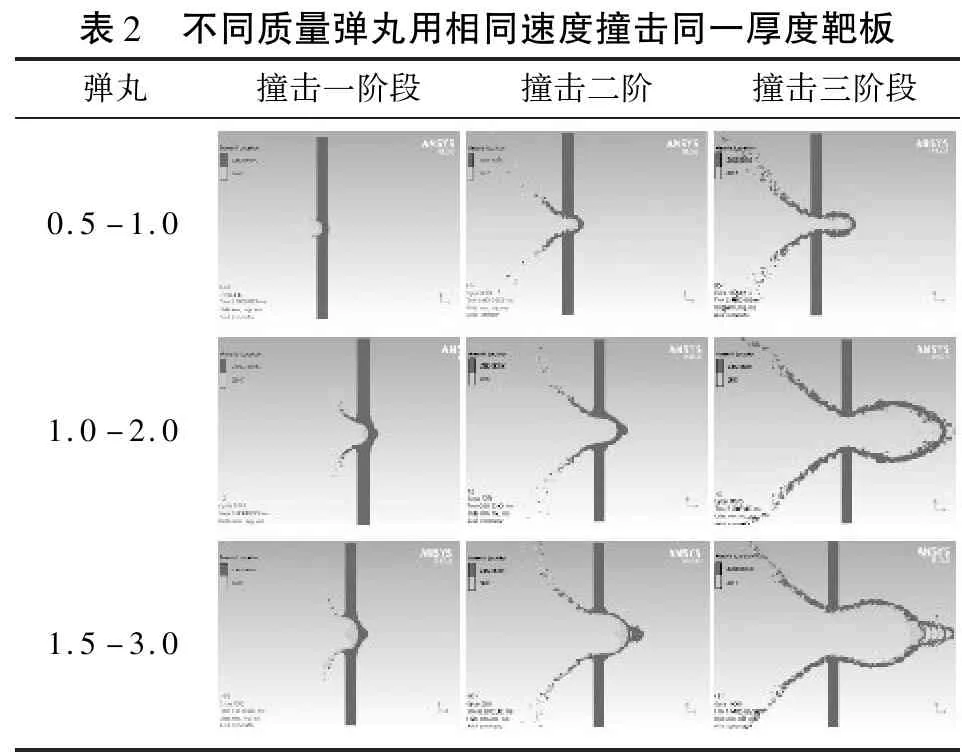
表2 不同质量弹丸用相同速度撞击同一厚度靶板弹丸撞击一阶段撞击二阶撞击三阶段0.5-1.01.0-2.01.5-3.0

2.3 弹丸撞击不同厚度靶板的破坏模式

在弹丸撞击不同厚度靶板的破坏模式中,分别选择1.0,2.0,3.0,4.0mm厚度的ZrB2-30SiC复合陶瓷板,速度和弹丸大小均为定量,其中选择速度为3km/s,弹丸半径为1mm,长度为3mm的圆柱型弹丸,其三个阶段的破坏情况见表3。

由表3可知,第一阶段弹丸由于压缩末端发生层裂并且膨胀,最前端由于碰撞发生破碎,靶板由于冲击产生反溅碎云片,靶板被弹丸侵蚀;板厚较小时,靶板后壁有明显鼓包,板厚较大时,靶板后壁无明显变化。第二阶段弹丸末端发生剥落,弹丸基本完全破碎,弹丸完全穿过靶板产生穿孔,在板厚较大时,穿孔形状为尖状(板厚为4mm时),这是由大,穿孔半径亦越大。

表3 弹丸撞击不同厚度靶板各阶段的破坏模式板厚/mm撞击一阶段撞击二阶段撞击三阶段1.02.03.04.0

2.4 弹丸未撞穿靶板的破坏模式分析

由以上三种情况的数值模拟,研究弹丸撞击靶板的能量为何值时,靶板不出现破坏情况。因为增加板厚并不能使穿孔半径降低,选择1.0～2.0mm厚度的靶板时穿孔半径基本不变,所以在弹丸未撞穿靶板的损伤分析中,选择ZrB2-30SiC复合陶瓷靶板厚度均为2.0mm,利用插值法进行数值模拟研究,见表4。

由表4可知,用0.5-1.0弹丸在1km/s状态下撞击靶板,弹丸无法穿透靶板;0.5-1.0弹丸在1.3km/s状态下撞击靶板,形成贯穿裂纹,弹丸嵌入靶板中间;用0.5-1.0弹丸在1.5km/s状态下撞表4 弹丸穿透相同厚度靶板临界值的各阶段破坏模式速度/(km/s)弹丸撞击击靶板，弹丸穿透靶板。因此，靶板的击穿临界速度约为1． 3 km/s(0．5-1．0 弹丸) 。

一阶段撞击二阶段撞击三阶段1.00.5-1.01.30.5-1.01.50.5-1.0注:第二行第三幅图为局部放大图。

3 结语

在不同速度和质量弹丸撞击靶板的破坏模式研究中，穿孔半径变化规律为穿孔半径随着弹丸速度和质量的增大而增大。在弹丸撞击不同厚度靶板的破坏模式研究中，增加板厚会引起穿孔直径的增加。对弹丸未撞穿靶板的破坏模式分析，经过数值模拟研究，只有半径为0.5 mm长度为1.0 mm的弹丸不会对靶板破坏，同时获得靶板的击穿临界速度为1.3 km/s(0.5-1.0弹丸)。