基于密度的进化算法的机械产品选配方法
2020-03-19段黎明涂玉林李中明罗雪清任华桥
段黎明,涂玉林,3,李中明,3,罗雪清,3,任华桥,3
(1.重庆大学 光电技术及系统教育部重点实验室ICT研究中心,重庆 400044;2.重庆大学 工业CT无损检测教育部工程研究中心,重庆 400044;3.重庆大学 机械学院,重庆 400044)
0 引言
在机械产品的生产过程中,考虑到加工精度和生产成本的约束,一般采用选择装配(简称选配)方法来保证产品装配精度,提高产品质量。
目前,国内外学者针对机械零件选择装配的相关问题已提出一些解决方法。张宇等[1]为了提高产品装配精度,提出一种统计分组装配技术;Kumar等[2]分析了机械零件的多种制造公差对装配精度的影响,提出一种基于遗传算法的分步分组选配方法;Matsuura等[3]分析了测量误差对装配精度的影响,提出基于间隙变动影响的分组选配方法;Fei等[4]为了提高选配成功率,基于遗传算法提出一种分组数随机的分组选配方法;杨枨等[5]为了提高机械产品性能,建立公差分组数学模型并提出一种基于成分最小化的分组装配方法。以上研究成果主要针对单一目标进行优化,而且适用范围具有局限性。
Raj等[6-7]采用遗传算法和粒子群优化算法选择装配零件,但其优化模型不适用于多尺寸链问题;宿彪等[8]针对再制造选配问题提出一种面向再制造的选配方法;李明周等[9]针对曲柄连杆机构的选配过程,提出一种基于混合算法的选配方法来满足其中的多种装配要求;Jeevanntham等[10]针对复杂机械产品,采用模糊进化算法求解选配问题;Matsuura等[11]和Akansel等[12]通过改变零件的尺寸公差值与其他零件配合,较好地提高了选配成功率;任水平等[13]针对机械产品多尺寸链问题,综合强弱Pareto与密集度构造适应度函数,提出一种基于遗传算法的选配方法;王康等[14]采用改进的基于强度Pareto进化算法解决选择装配问题,将其应用于复杂机械产品。以上研究成果主要基于进化算法的产品选配方法,可以解决多目标优化问题,但是在保证解群体分布性上有所欠缺。
综上所述,选配问题研究存在优化目标单一、容易陷于局部最优等问题。为此,本文在机械产品的多目标多质量要求下,引入基于密度的多目标进化算法[15](Density-based Multi-Objective Evolutionary Algorithm, DMOEA),提出一种针对机械零部件的选择装配方法。首先,建立零件尺寸链与尺寸的关联关系,以选配成功率和装配精度作为优化目标构建选择装配数学模型;然后,利用个体密度定义个体适应度函数,将其作为机械产品选择装配多目标多质量要求下的个体评价规则,采用DMOEA选配算法寻优,最终得到Pareto最优装配方案。
1 零件选择装配数学模型的建立
1.1 约束定义
在机械产品装配中,装配尺寸链指不同零件尺寸按特定顺序排列而成的封闭尺寸组。装配过程中用来表示装配精度的尺寸称为封闭环,余下尺寸被称为组成环。组成环中,按照其对封闭环的影响分为增环和减环。构建装配尺寸链与零件尺寸的关联关系矩阵R,

(2)
式中rm,k表示第m个尺寸链与第k个尺寸的关联关系。
机械产品的装配质量主要与产品各个尺寸链的封闭环有关。根据封闭环的尺寸要求,建立尺寸链约束条件矩阵g,
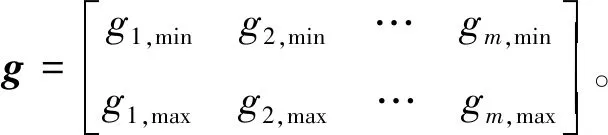
(3)
式中:gm,min,gm,max分别表示第m个尺寸链封闭环的上、下偏差。
定义尺寸数据
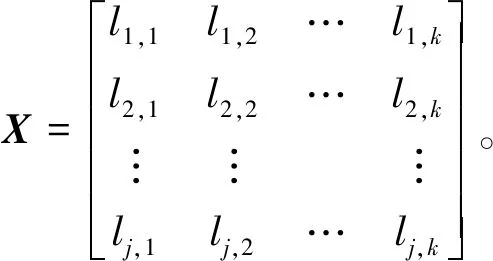
(4)
式中lj,k为第j组零件第k个尺寸的实测值。
如果一组零件的配合间隙在要求范围内,则称该组零件的尺寸链合格,即

(5)
式中gm,j为第m个尺寸链的第j组零件装配后的封闭环的实测值。
1.2 目标定义
1.2.1 选配成功率
选配成功率指一次选配得到的合格产品数量与其中装配出的产品数量的比值,即
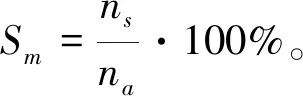
(6)
式中:Sm为第m个尺寸链的选配成功率;ns为第m个尺寸链中成功选配的零件组量;na为第m个尺寸链中参与选配的零件组数。
1.2.2 装配精度
为了提升产品性能,不但要满足设计要求,还要使产品配合间隙尽可能接近其对应的最优间隙,而且在满足机械产品装配要求的同时,装配精度越高越好。借鉴田口质量模型[16]构建装配精度的评估模型,本文以选配零件的配合间隙偏离最优间隙的平均质量损失为优化函数,定义质量损失函数C(gm,j),并采用第m个尺寸链的质量损失评估其装配精度Qm。质量损失函数的数学表达式为
C(gm,j)=
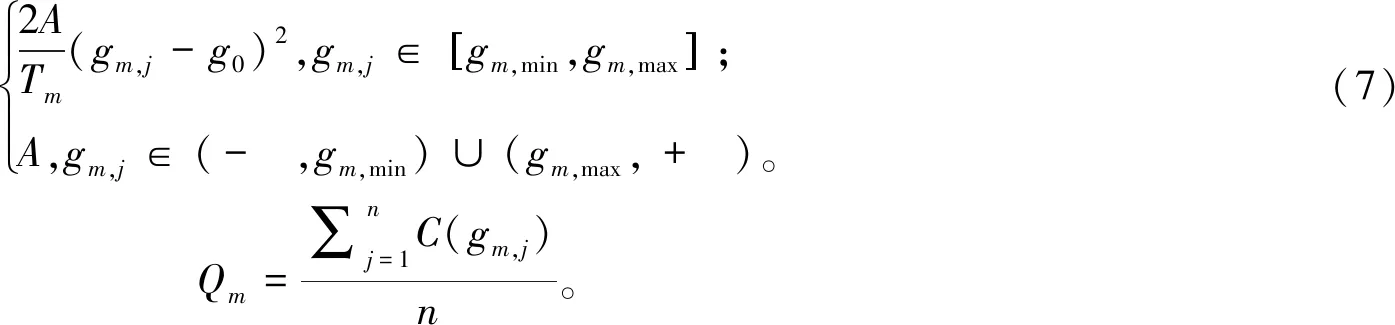
(8)
式中:A为产品装配不合格时的质量损失;g0为第j组零件第m个尺寸链的最优间隙值;Tm为第m个尺寸链的设计公差;n为选配方案中的产品数量。
1.3 多目标多质量选配模型
产品选配方案的优劣由选配成功率与装配精度共同评价,由此提出单质量综合优化目标函数
Mm(X)=αQm(X)+(1-α)(1-Sm(X)。
(9)
式中:α(0≤α≤1)为定值,表示选配方案中装配精度的重要系数;Qm为装配精度,其值越小,装配精度越高,因此优化方向为极小值方向。根据多目标单质量要求下的目标函数,定义多目标多质量要求下的选择装配模型为
minfitness(X)=[M1(X),…,Mm(X)]。
(10)
2 基于密度的多目标进化算法的选配模型
DMOEA通过计算每个解个体的密度来保持解群体的多样性,使算法在收敛时具有良好的分布性。在分布性方面,DMOEA比基于强度的Pareto进化算法2[14](Strength Pareto Evolution Algorithm 2,SPEA2)和非支配排序遗传算法2[17](Non-dominated Sorting Genetic Algorithm 2,NSGA2)等均有较大程度的提高。本文的DMOEA通过修剪、适应度分配和繁殖选择使繁殖进化群体中的非支配合个体具有较好的分布性,从而得到非支配集,最终输出多个非劣解。
2.1 进化算法的编码方式
配对编码是对每个方案中零件尺寸值编号进行配对的编码。配对编码的基因是同一组零件尺寸值编号的随机序列,记为βj。一个染色体由多个配对编码基因组成,记做Xi(i为种群序号),
Xi=[β1,β2,…,βj,…,βw]。
(11)
式中w为参与选配的零件尺寸个数。
2.2 基于密度的多目标进化算法
2.2.1 目标空间的支配关系

2.2.2 适应度分配策略
采用个体聚集密度作为DMOEA的适应度分配策略。为了量化任意两个个体间的影响程度,采用正态分布的密度函数,定义为

(12)
式中:σ为分布程度的标准偏差,r为个体间的欧氏距离。
解个体的密度指解群体中每个体对其影响因子的聚集程度,结合正态分布的密度函数,得到解个体xy的密度的数学公式为

(13)
式中:xi∈Pt,xy∈Pt,Pt为繁殖进化群体;l(xi,xy)为个体xi到个体xy之间的欧式距离;D(xy)为解个体xy的密度。
将fitness(x)/D(x)定义为个体x基于密度的适应度,则适应度函数
(14)
适应度大的个体的密度小,即其他个体对其影响的程度小,在进化过程中将其淘汰,保留适应度小的个体进入下一代,以保持解的多样性。
2.3 基于密度的多目标进化算法流程
本文提出的DMOEA是对传统多目标进化算法的改进,其算法流程与基于Pareto的多目标进化算法的一般流程类似。首先随机产生初始进化群体和繁殖进化群体,通过繁殖选择、修剪、交叉、变异等操作不断促进进化,然后将选配成功率和装配精度作为指标比较选配方案的优劣并进行排序,最后在满足终止条件后输出最优解。
(1)繁殖选择
在对繁殖进化群体进行繁殖操作时,优先选择个体聚集密度较小的个体。
(2)修剪过程
若繁殖进化群体Pt大于规定值N,则采取某种方式减少其规模,同时保证其较好的分布性,该操作称为修剪。
在执行修剪操作时,淘汰繁殖进化群体中密度最大的个体,若每个个体密度相同,则淘汰随机抽取的个体。继续该操作使繁殖进化群体的大小等于规定值。每次淘汰一个个体时,余下个体需重新计算其适应度值。
(3)交叉操作
本文采用单点交叉法进行交叉操作,具体是将双亲个体从第j个基因处截断(j为随机数,且j∈{1,2,…,n-1}),然后交换双亲染色体的第{j+1,j+2,…,n}个基因。
(4)变异操作
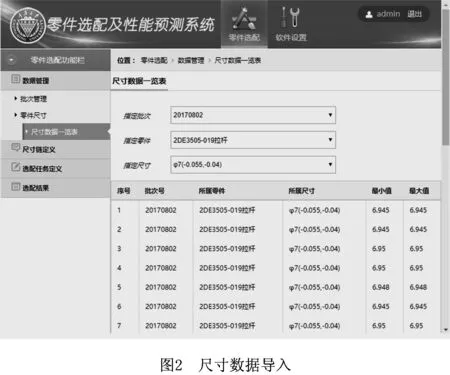
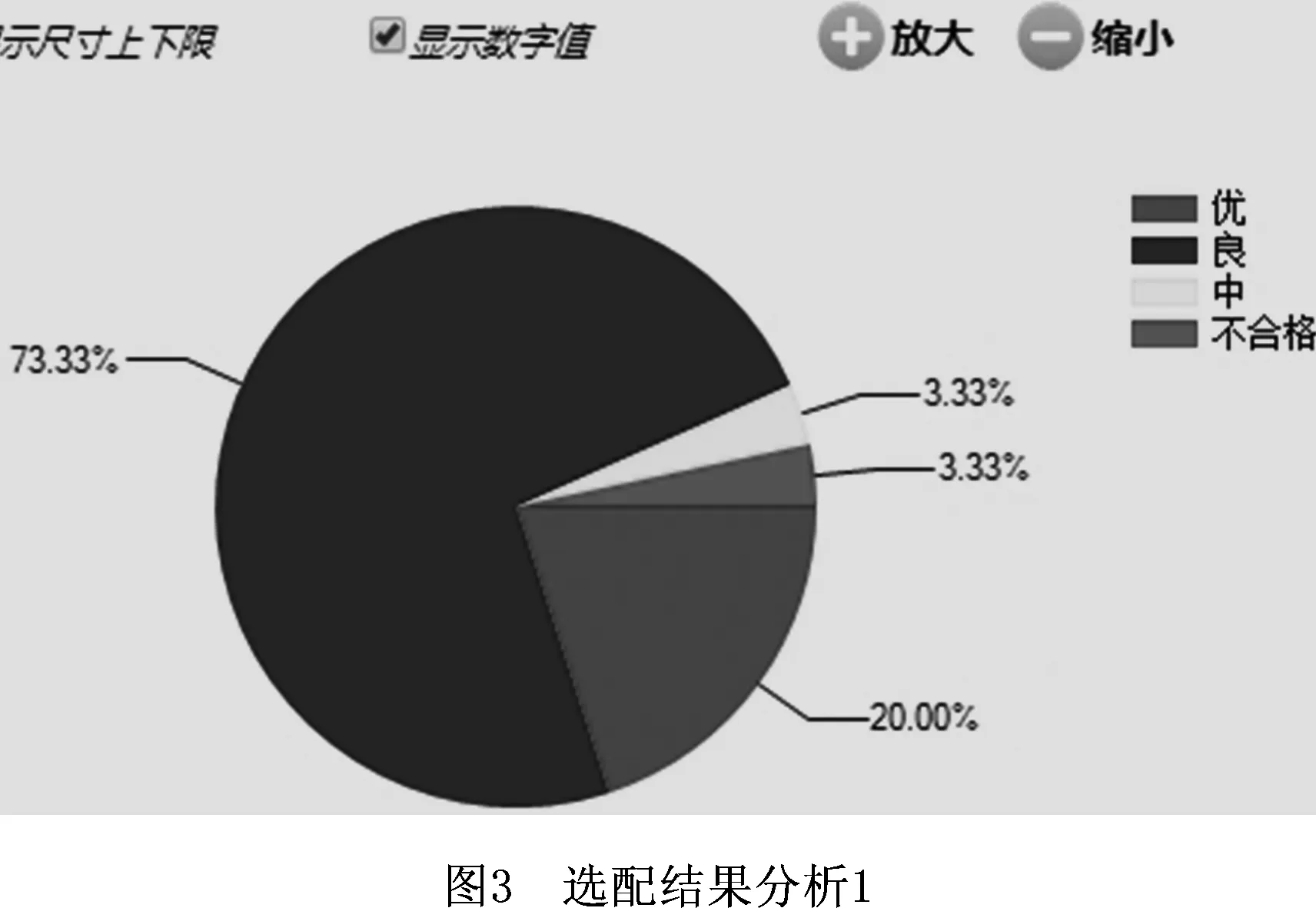
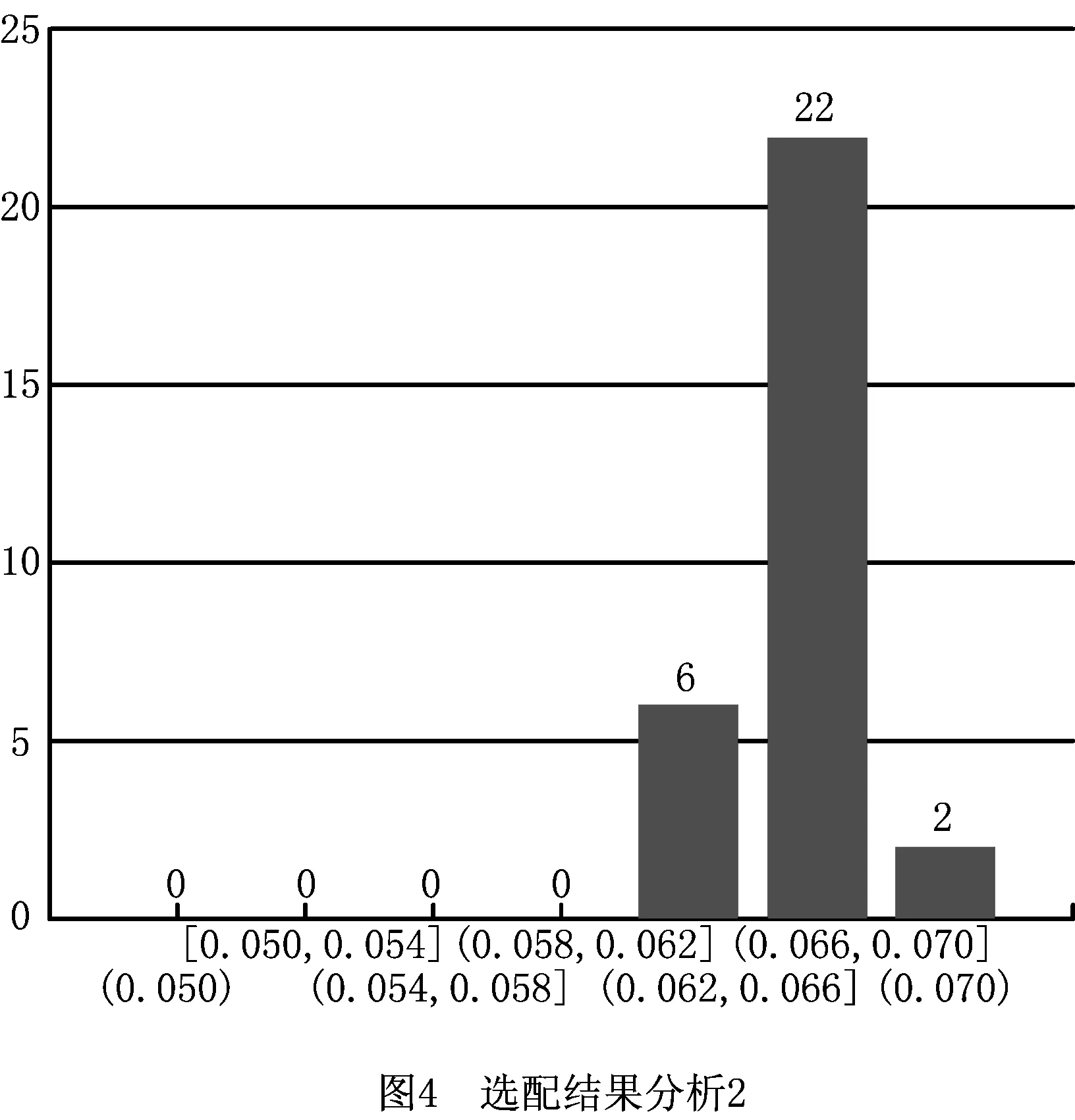
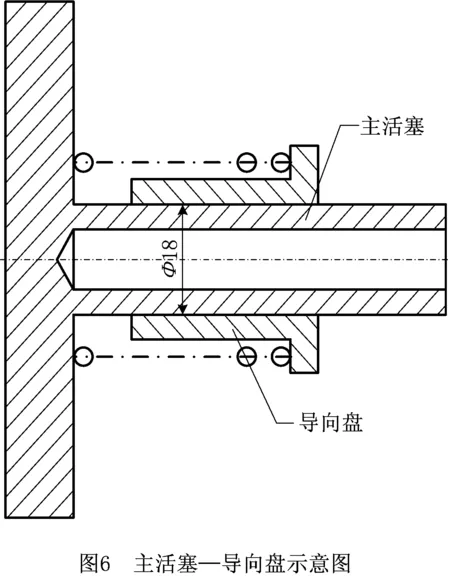
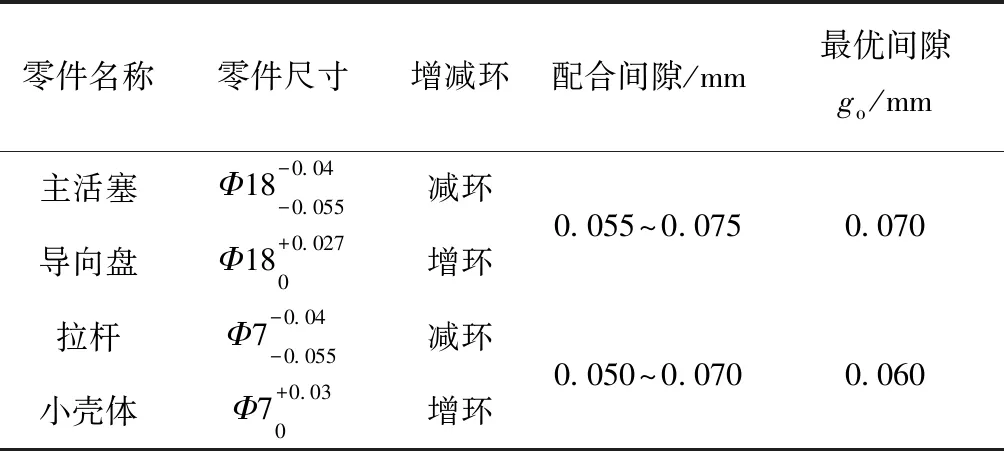
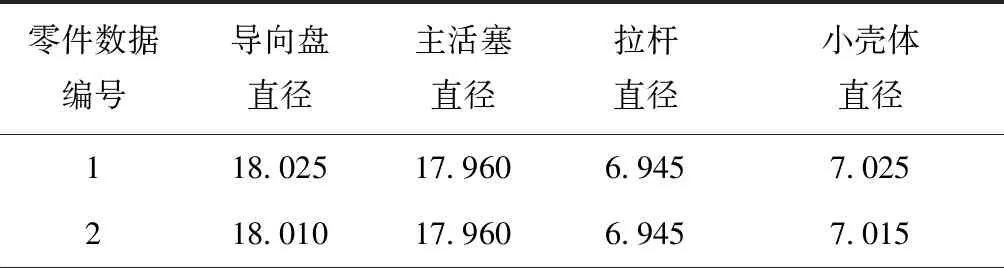
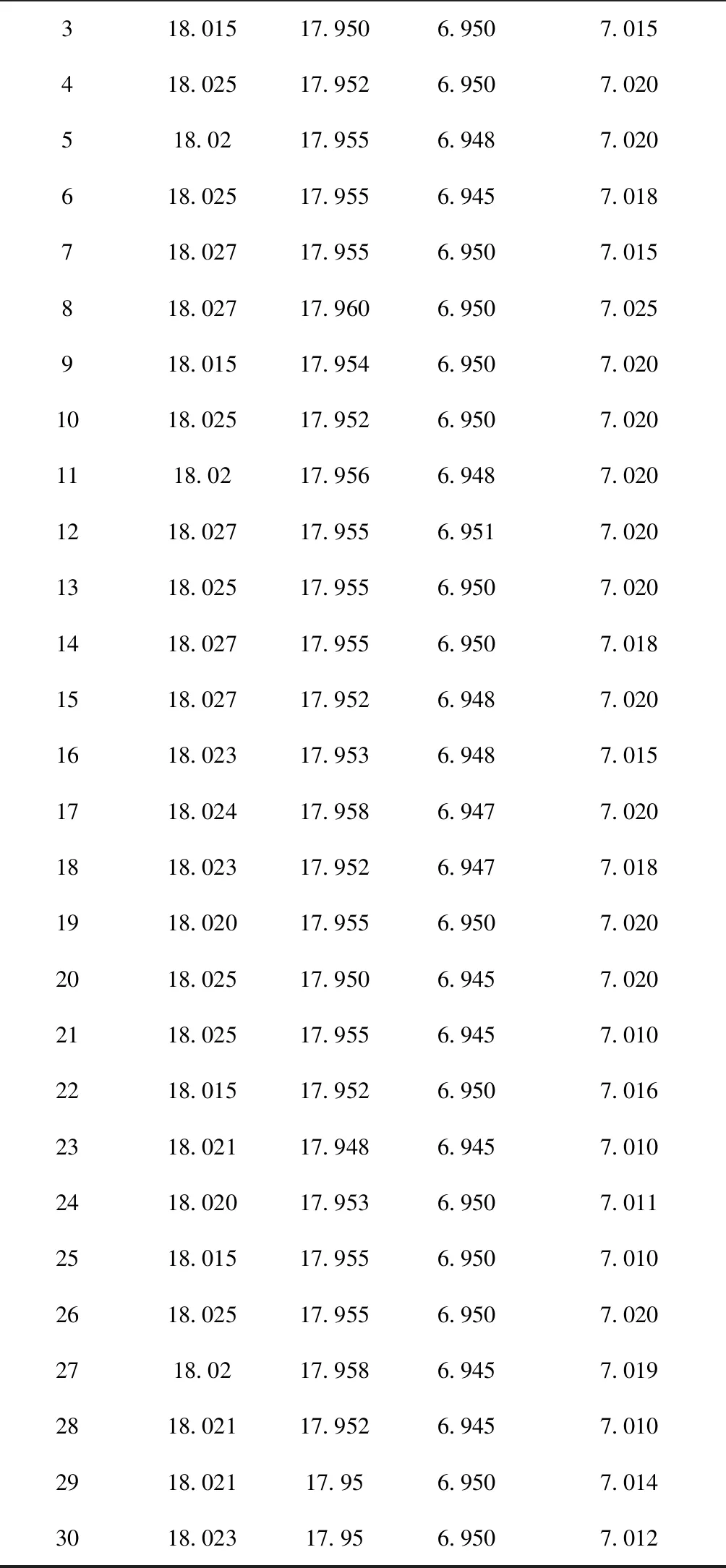
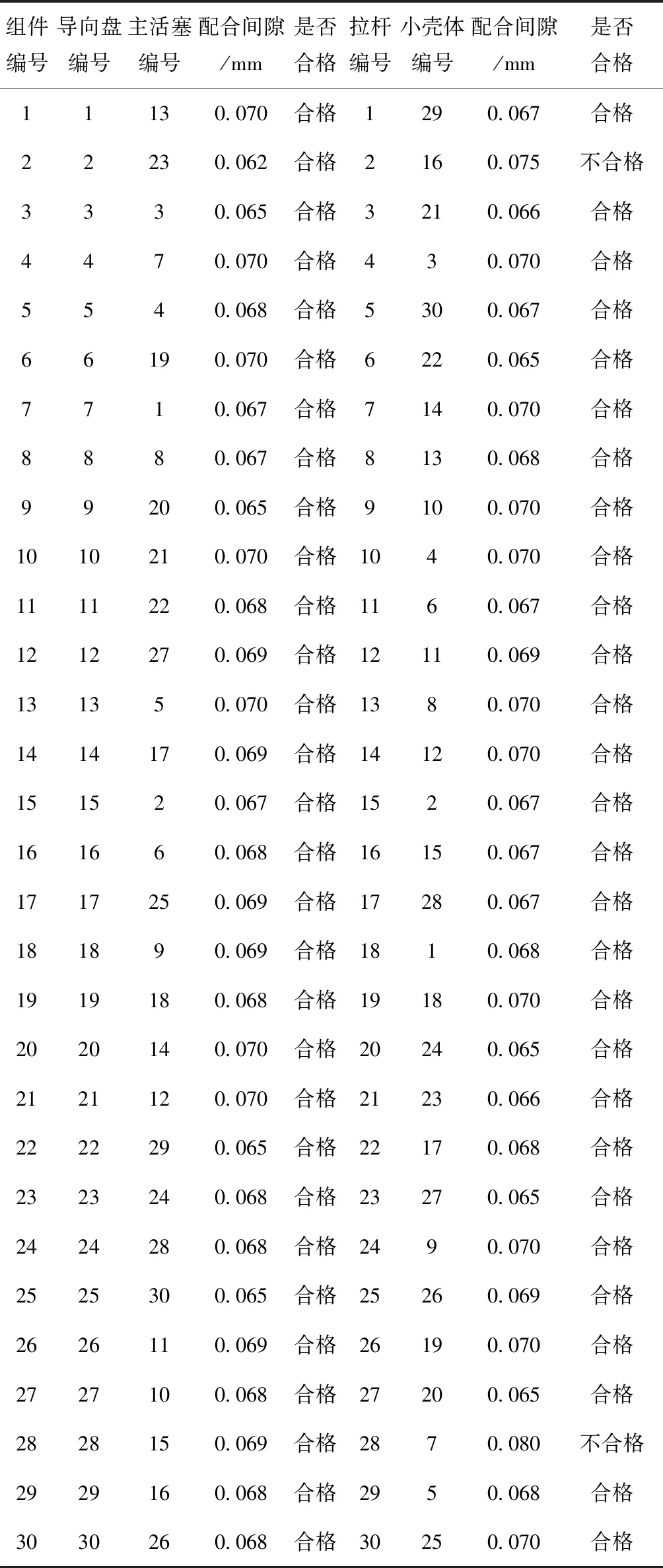
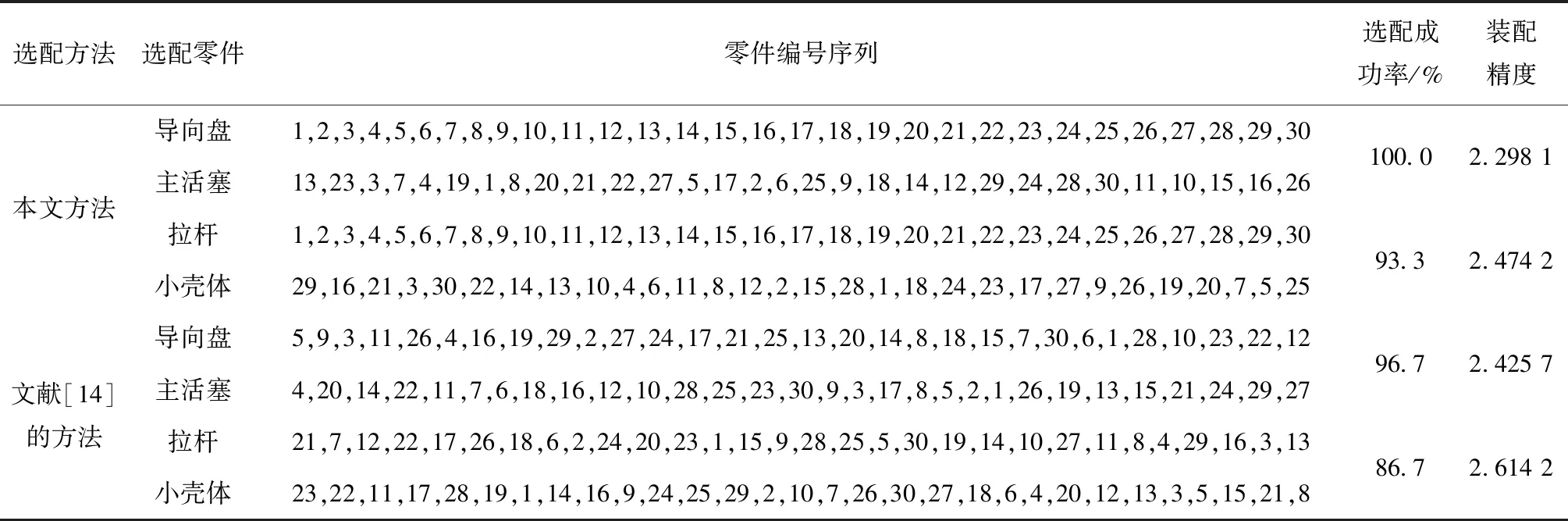
对每条染色体的每个基因生成一个随机数r,r∈(0,1),若r DMOEA流程如图1所示,具体步骤如下: (1)生成初始环境进化群体R0和繁殖进化群体P0,并使P0=∅,其中|Pt|=N,|Rt|=2N,令迭代次数t=0,最大进化代数为Z。 (2)进行环境选择。构建环境进化群体Rt的非支配集,并将非支配集中的个体复制到Pt+1和Rt+1中。 (3)若|Pt+1|>N,则计算Pt+1中个体的适应度,然后对Pt+1进行修剪,使其进化规模为N;若|Pt+1| (4)若t (5)对繁殖进化群体Pt+1进行繁殖选择。 (6)对繁殖进化群体Pt+1进行交叉和变异操作,将所产生的新个体复制到环境进化群体Rt+1中,令t=t+1,转(2)。 针对某公司××型号机械产品选择装配的实际问题,开发出基于DMOEA的零件选配系统。为了将零件选配系统与在线监测进行融合,采用浏览器/服务器(Browser/Server,B/S)架构,系统主要分为数据管理、尺寸链定义、选配任务定义和选配结果4部分。应用效果如图2~图5所示。 ××型号产品主要包括主活塞—导向盘、拉杆—小壳体两部分,其示意图如图6和图7所示,其零件数据如表1和表2所示。 表1 选配用到的零件 零件名称零件尺寸增减环配合间隙/mm最优间隙go/mm主活塞Φ18-0.04-0.055减环导向盘Φ18+0.0270增环0.055~0.0750.070拉杆Φ7-0.04-0.055减环小壳体Φ7+0.030增环0.050~0.0700.060 表2 某公司活门部分零件数据 mm 续表2 相应的零件尺寸链与尺寸的关联关系为 (15) 构建××型号产品零件选配数学模型时,若设定装配不合格,则质量损失值A=20。设N=50,Pc=0.8,Pm=0.1,Z=100,σ=0.2,在零件选配系统中求解模型,得到的零件选配结果如表3所示。 表3 主活塞—导向盘、拉杆—小壳体的选配结果 在相同的原始数据下,将基于SPEA2的选配方法[14]与本文基于DMOEA的选配方法进行比较,结果如表4所示。可见,在选配成功率与装配精度方面,本文方法优于基于SPEA2的选配方法。 表4 不同选配方法的选配结果对比 本文针对机械产品多目标多质量要求下的选择装配问题,提出一种基于DMOEA的选配方法。该方法采用选配成功率和装配精度作为指标比较选配方案的优劣,在算法中利用个体密度定义个体适应度函数,构造分布性良好的群体,从而得到更好的搜索结果。最后通过对比实验证明本文方法的选配成功率更高、装配精度更好。所开发的系统已成功应用于某公司产品的零件选配过程中,从实际应用效果分析,基于群体分布性的算法的鲁棒性更好,受遗传算子随机参数的影响更小,实用性更强。 本文采用了正态分布定义距离算子,是否存在x正向单调递减函数使群体分布性更好,可以作为后续研究的方向。
3 应用实例及分析


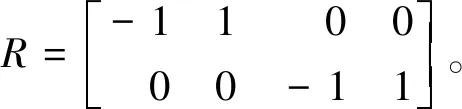
4 结束语
