结合暗通道先验与Hessian正则项的图像去雾

高珠珠， 魏伟波， 潘振宽， 赵 慧

(青岛大学计算机科学技术学院，山东 青岛 266071)

空气中的悬浮颗粒使得大气光发生散射作用，因此，恶劣天气下拍摄的图像通常对比度差、颜色灰暗，严重影响图像质量，也对视频监控、智能车辆、卫星成像、目标识别等计算机视觉应用领域造成困惑[1]。因此，通过图像去雾而获得清晰、高质量的图像对计算机视觉应用与图像处理意义重大。

通常，图像去雾就是去除有雾图像中的雾度并重建自然场景原始颜色的过程。例如，直方图均衡化[2]、小波变换[3]、多尺度Retinex算法[4]，均可对已降质的图像进行增强，有效地提高雾天图像的对比度，增强图像的细节，改善视觉效果，但这些方法未考虑如雾霾浓度差异以及浓度与物体深度成正比的关系，因此通常不能自适应的去雾。雾天图像复原是研究雾天图像退化的物理机制，并建立雾天退化模型，反演退化过程，补偿退化过程中造成的失真，以便获得未经干扰退化的无雾图像或无雾图像的最优估计值，从而改善雾天图像的质量。其针对性强，得到的去雾效果自然，一般不会有信息损失。如文献[5-8]的算法，其中，利用暗通道先验的文献[8]算法是当前最具代表性的去雾复原方法之一，该方法假设在绝大多数非天空的局部区域中，某些像素总会有至少一个颜色通道具有很低的值。文献[9-10]对基于暗通道先验的去雾方法进行了进一步的完善，但在天空区域去雾效果不佳，且去雾后图像中的噪声也随之增加。

现有的去雾方法大多是基于深度信息的方法，是因为去雾性能高度依赖于准确的深度信息。为了保证高质量的去雾，有必要在图像去雾时准确地估计深度信息。因此，FANG等[11]提出了一个全变差的变分框架，可同时估计深度图和去雾图像，其中的 TV正则项能够保留深度图与去雾图像的主边缘，并能抑制一部分噪声，提高了去雾图像的清晰度[12-13]。然而，基于TV正则项的处理方法往往会产生阶梯效应，作为 TV正则项的延伸，二阶的Hessian正则项具有保留精细结构同时抑制阶梯伪影的能力，且二阶微分比一阶微分更适合用来刻画图像的振荡性[14]。因此，为了进一步提高去雾性能，本文首先利用暗通道先验方法求得原始透射率图，然后将Hessian正则项用于透射率图与去雾图像的估计，提出了相应的模型，并为其设计了ADMM (alter direction method of multipliers)算法，该方法相比于其他求解能量泛函的方法，如对偶算法[15]，效率相对较高。最后，对薄雾及浓雾图像的去雾效果进行了主观及客观的评价与分析。

1 暗通道先验方法和变分模型

本节将对暗通道先验方法与Hessian正则项变分模型进行详细地介绍。

1.1 暗通道先验方法

SCHECHNER等[16]基于MCCARTNEY的大气散射模型，提出了单色大气模型来模拟雾天环境下的退化过程，模型如下

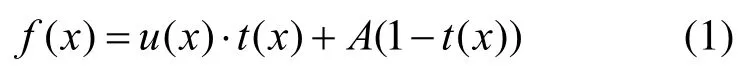
其中，f为有雾图像；u为去雾后的图像；A为像素位置，即全局大气光，代表周围环境中各种光的总强度；t为透射率图，反映了场景目标的深度信息，t= e-βd，β为大气散射系数，d为场景深度；通过求取t，A值可从有雾图像f中得到去雾后的图像u。

去雾的目的在于通过对有雾图像的处理得到类似于在晴朗环境下拍摄的图像，即去雾后的图像应满足对大量无雾或晴天图像的统计规律，所以，文献[8]利用数理统计方法，通过对5 000幅户外晴朗条件下拍摄的无天空图像，对其像素亮度值的累积直方图进行统计得出暗通道先验规律：在大多数无雾图像中的局部区域内，其一些像素会在某个通道内具有非常低的像素值。低像素值的产生主要是由于阴影，当彩色物体在某一个通道的值太大时，其他通道的值会很小。因此，可按块求出图像的暗通道图像，即

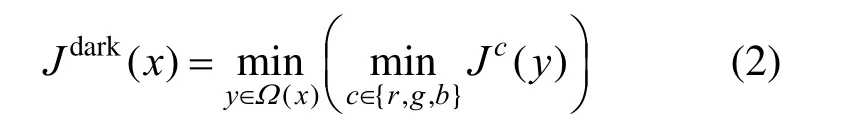
其中，Jc为彩色图像J的每个通道；Ω(x)为以像素x为中心的一个窗口。将式(1)两边同时除以Ac，并对两端的像素块取最小值得到

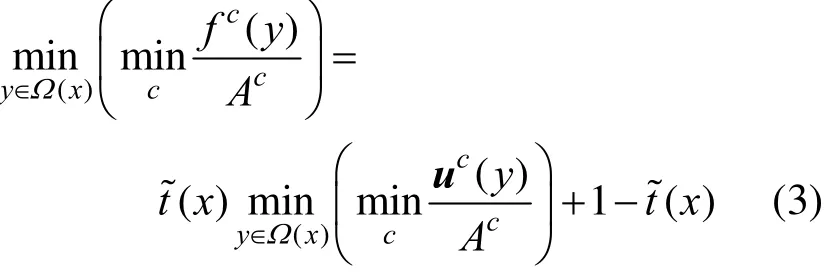
其中，Ac为在暗原色图像中像素强度最强的点的像素值。在Ω(x)邻域中，t(x)为常数，记为t~(x)。由暗原色先验可知，去雾后图像的暗原色通道u应趋于0，且Ac总是一个正数，故可以表示为将式(4)代入式(3)，可以消除多个参数并且得到透射率的粗略估计表达式为

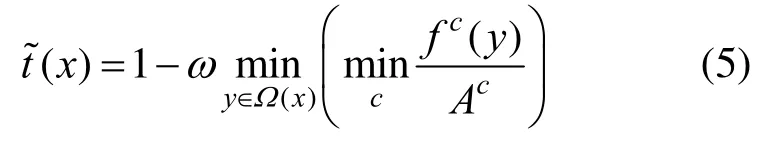
其中，ω为一个固定的参数值(0<ω≤1)，ω是为了留有一定浓度的雾而设置的，可以使恢复后的图像能保留一定的景深，主观感受更加自然。ω值是基于应用场景的，通常设置为0.95。

文献[8]算法利用暗通道先验规律来估算大气光值。在暗通道图像中，将各像素点的亮度值按递减的顺序排列，确定数值为前 0.1%的像素点所处的位置，其所对应的原有雾图像区域中的最大值即为大气光值A。最终，暗通道先验模型复原图像公式为

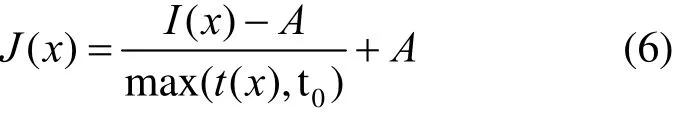
其中，t0为避免除数为零而设置的一个常数，一般取值为0.1。

1.2 Hessian矩阵变分模型

Hessian矩阵描述图像二阶导数的特征，可以增强图像线状结构[17]。Hessian矩阵变分模型在对图像进行平滑处理的同时，能够检测到图像的振荡等特征，在消除噪声的同时较好地保持了图像的细节特征，得到了较为满意的结果，即

其中，彩色图像有R，G，B3个通道，所以f=[f1f2f3]T，u=[u1u2u3]T。f为噪声图像；u为修复图像；i为彩色图像的R，G，B通道。式(7)等式右边的第一项为HMV模型的正则项，λ为调节参数，表示恢复后图像光滑程度的先验知识；第二项为数据项，表示观测图像与恢复后图像的接近程度。

2 本文去雾模型及ADMM算法

根据Hessian正则项[17]的优势，本文以透射率图t(x)与去雾图像u(x)建立的去雾模型为

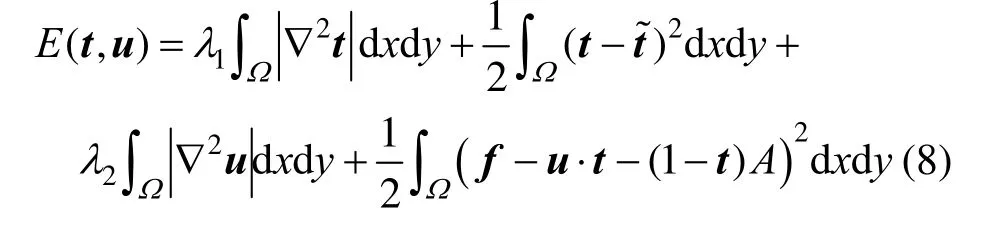
其中，t为待求解的透射率图；为式(5)所求得的原始透射率；为透射率图的数据项，在其他项的约束下，最小化该项使得透射率t在同质区域内其值逐步逼近于，保证在同质区域内待求解透射率的精确性和同质性为透射率图的正则项，将其最小化，可得到整幅有雾图像的定义域内透射率的梯度值最小，实现透射率的全局平滑。为去雾图像正则项，项保证了被恢复图像与原图像的逼近。f为有雾图像；u为去雾后的图像；1γ为透射率图扩散项参数，控制图像的光滑程度；2γ为去雾图像扩散项参数，控制图像的光滑程度；A为大气光值。

为了便于求解，将式(8)分解为式(9)和式(10) 2部分。式(11)和式(12)是式(9)和式(10)的ADMM求解过程，即

为式(9)引入辅助变量p，w1，w2，w3，w4。设令p=∇x，w4= ∂yp2。w1=∂xq1，w2= ∂yq2，w3= ∂xq3，w4= ∂yq4。其中，β1，βp为惩罚参数；γ1，γ2，γ3，γ4，γp为拉格朗日乘子。得到式(11)，即E(t,p,w1,w2,w3,w4)=

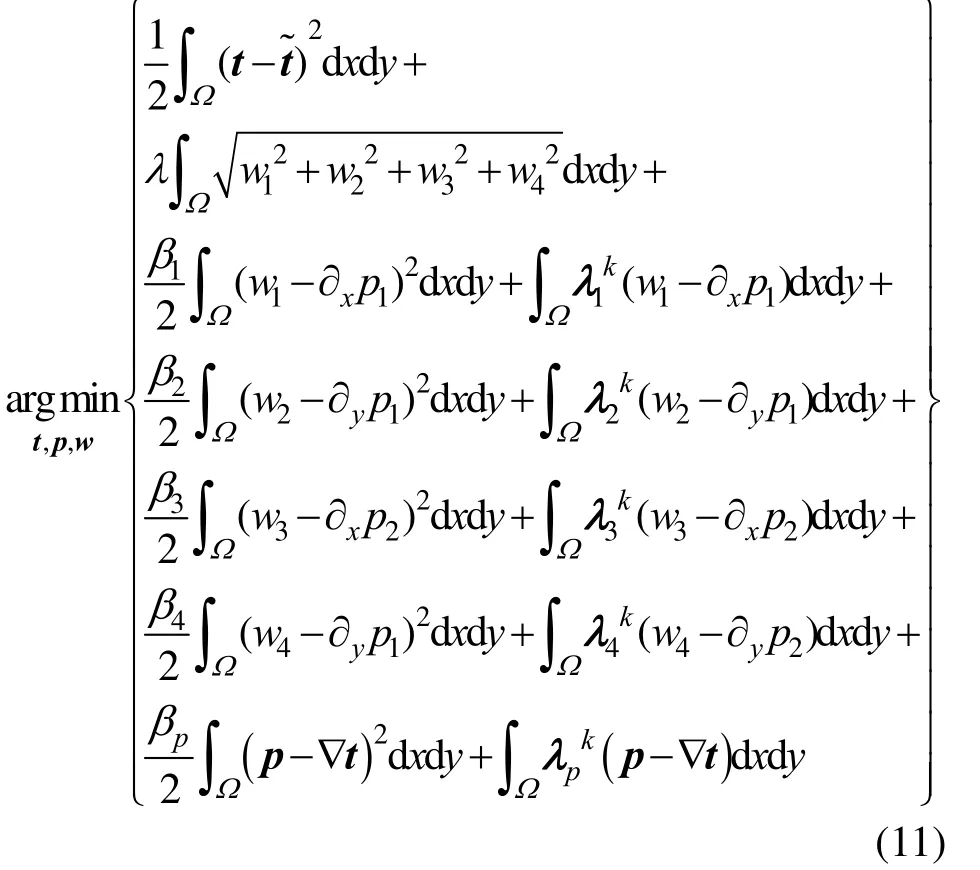
为式(10)引入辅助变量q，v1，v2，v3，v4，设令v4= ∂yq4。其中，θ1，θp为惩罚参数，α1，α2，α3，α4，αp为拉格朗日乘子。得到式(12)

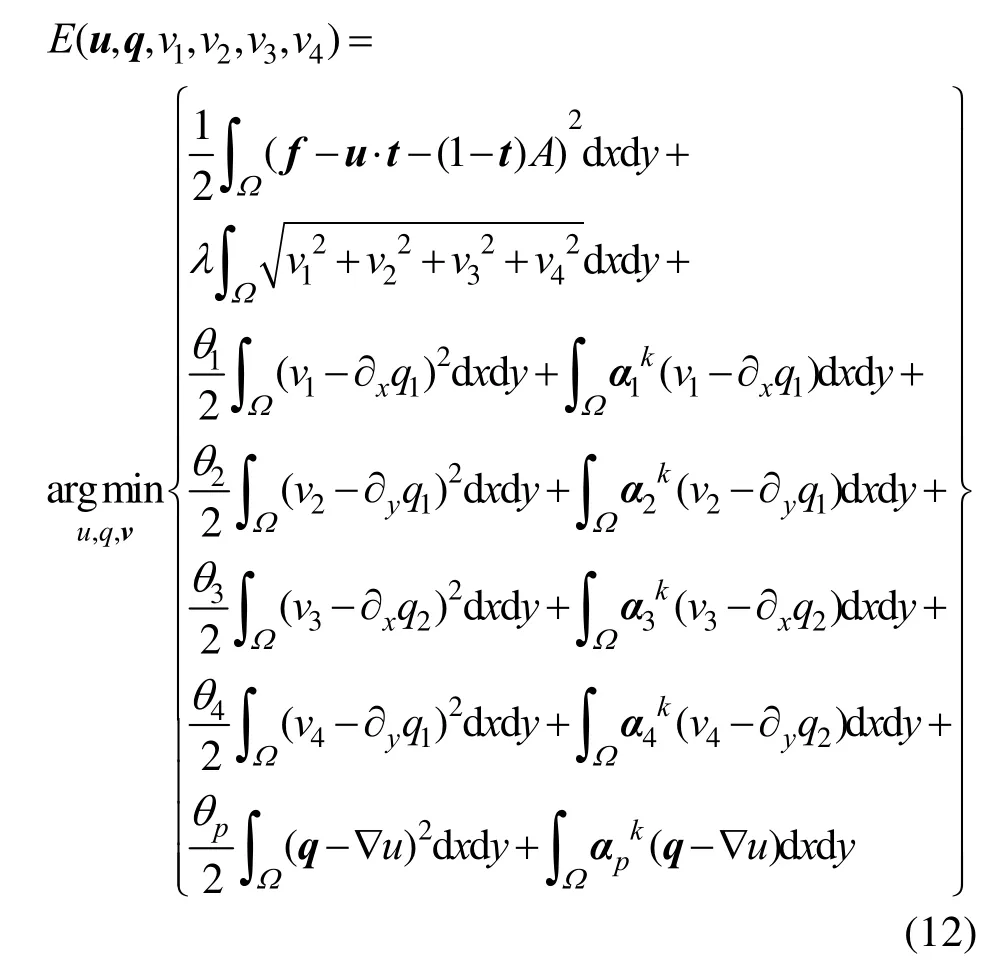
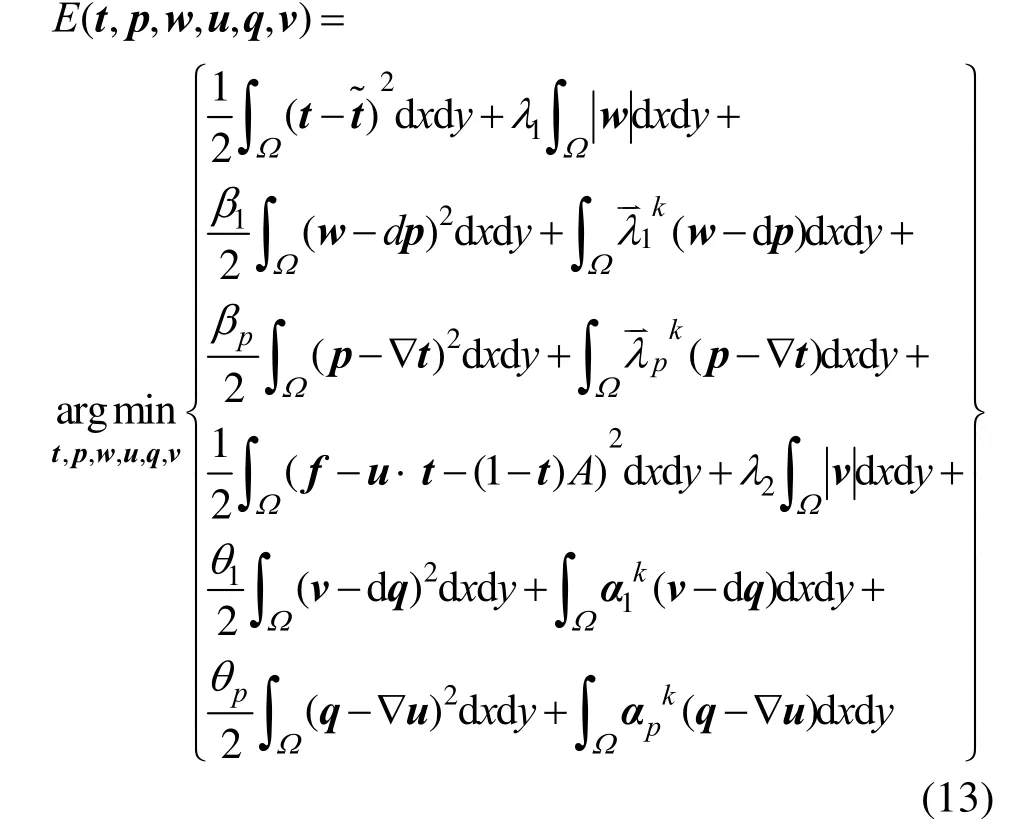
具体迭代g过程为

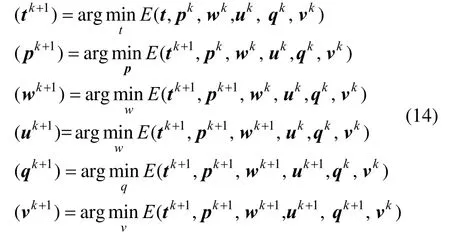
更新拉格朗日乘子

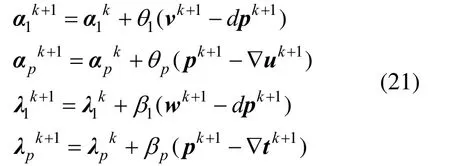
式(15)，(17)，(18)和式(20)是关于tk+1，pk+1，uk+1，qk+1的欧拉-拉格朗日方程，式(16)和式(19)是关于wk+1，vk的广义软阈值公式。式(15)，(17)，(18)和式(20)均可用 Gauss-Seidel迭代方式进行求解，分别求出tk+1，uk+1。

本文模型求解步骤如下：

输入：有雾图像f。

输出：去雾图像u。

步骤 1.输入有雾图像，利用暗通道先验估算出透射率和大气光值A。

步骤 2.初始化，设置模型的调节参数、拉格朗日乘子、惩罚参数、以及迭代步数step=200。

步骤 3.根据欧拉-拉格朗日方程与软阈值公式求得各模型参数。

步骤 4.不断循环更新迭代拉格朗日乘子，直到 abs(E(step)–E(step–1)/E(step))<0.01，E(step)代表第step步的能量值，即t，u均收敛。

步骤 5.输出t，u。

3 实验结果及分析

3.1 去雾方法流程

本文首先对有雾图像进行暗通道先验的处理，得到粗略的透射率图和大气光值，然后将粗略的透射率图结合Hessian正则项进行处理。同时，有雾图像结合Hessian正则项与大气散射函数得到本文统一的变分去雾模型，最后利用ADMM算法输出去雾后的图像。去雾算法流程如图1所示。

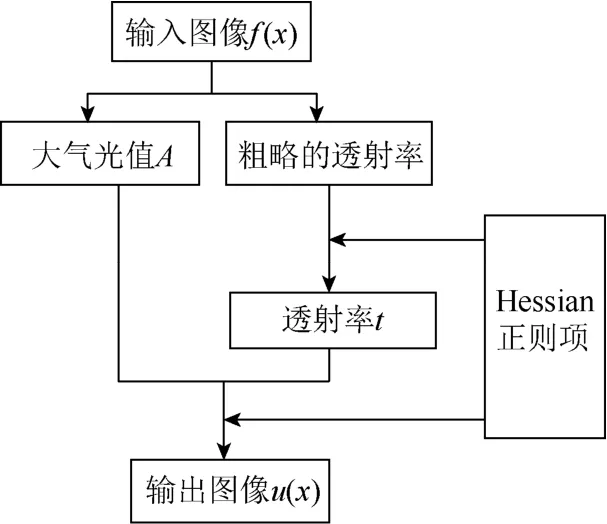
图1 本文算法流程图

3.2 仿真实验的主观评价与客观分析

本文用 Matlab(R2014a)对去雾模型进行了仿真实验，并与相关算法进行了比较。计算机配置为Intel(R) Core(TM) i5-4590 CPU @ 3.30 GHz， 4 GB RAM。

本文从LIVE Image Defogging数据库[18]中测试了大量有雾图像用于评估本文去雾模型的性能，并与有代表性的文献[5]、文献[6]、文献[19]、文献[8]和文献[7]算法以及近几年比较优秀的去雾算法文献[20]、文献[21]和文献[22]进行了比较。测试结果表明本文算法能有效地实现去雾，适用性较好。图2和图3是从LIVE Image Defogging数据库中随机挑选出的有雾图片以及各算法的去雾效果图。

本文对去雾图像进行2种客观评价算法，一种是全参考对比度增强评估，另一种是无参考感知雾密度评估。文献[23]提供了3个去雾算法评估的衡量标准，新增可见边之比e表示去雾图像中新的可见边缘相对于有雾图像的比率；饱和像素比率σ表示去雾后变成黑色或白色像素的百分比；描述的是平均可见度的增强程度。当e、为正且数值越大时，σ的值越接近于0，意味着性能越好。e，，σ3个衡量标准均属于全参考对比度增强评估。文献[24]提供的感知雾密度D是无参考感知雾密度评估方法，不需要有雾的原始图像，较低的D表示较好的去雾性能。

3.2.1 去除薄雾的主观评价与客观分析

图2以薄雾为例，从上至下3幅图像的各算法去雾效果图。从图 2中可以看出，图 2(b)文献[5]的去雾图像有些过饱和并伴随光环现象；图2(c)文献[6]算法消除了部分天际线附近的场景(第2行红框处)；图2(d)文献[19]算法去雾不够彻底，且纹理细节保持效果欠佳(第2行、第3行红框处)；图2(f)文献[7]产生了较灰暗的天空区域(第1行、第2行)；图 2(e)文献[8]与图 2(g)本文算法得到的去雾图像色彩更加自然，但本文算法比文献[8]算法显示出了更加清晰的细节(第3行红框处)。

表1中的数据是对图2的客观评价，可以看出，文献[5]算法去雾后虽然由于过饱和现象产生了最小的感知雾密度D以及较大的平均可见度，但e值出现了负值，说明该算法导致去雾后的图像失去了一些可见边缘；文献[6]和文献[19]算法产生了较大的雾感知密度D，说明2种方法去雾不够彻底，且文献[6]产生了较大的σ值；文献[7]算法由于去雾效果图过于灰暗，使得产生了较低的可见边缘；相比之下，本文算法产生了较小的雾感知密度D与最大的可见边缘e值，说明本文算法去雾更加彻底，纹理细节保持效果较好。

3.2.2 去除浓雾的主观评价与客观分析

图 3属于浓雾图像，展示了各算法去雾效果图，可以直观地发现图3(b)文献[18]算法去雾不够彻底，剩余的雾霾导致图像质量下降；图3(c)文献[21]算法存在过度平滑的现象；图3(d)文献[22]算法得到的图像整体亮度较好，但是部分区域过亮(如红框处)过曝现象明显，近景部分也出现过饱和现象。相比之下，图3(e)本文算法在保留图像细节的同时能够有效地去雾，其良好的性能主要得益于保留细节的Hessian正则项。

图2 本文模型与5种模型算法去雾效果对比

表1 图2中各算法定量比较(e，σ，，D)

表1 图2中各算法定量比较(e，σ，，D)

图像 文献[5] 文献[6] 文献[19]images/BZ_81_1038_2786_1051_2835.pngimages/BZ_81_1618_2786_1631_2835.pnge σr D e σr D e σimages/BZ_81_1038_2837_1051_2891.pngimages/BZ_81_1618_2837_1631_2891.pngr D第1排 –0.061 0.010 2.223 0.175 –0.122 0.025 1.562 0.362 0.010 0.011 1.625 0.416第2排 –0.143 0.024 2.343 0.116 –0.063 0.096 1.323 0.262 0.059 0.003 1.426 0.486第3排 0.080 0.11 2.284 0.181 0.044 0.021 1.231 0.511 0.098 0.004 1.621 0.515图像 文献[8] 文献[7] 本文images/BZ_81_1038_3045_1051_3094.pngimages/BZ_81_1618_3045_1631_3094.pnge σr D e σimages/BZ_81_1038_3096_1051_3141.pngr D e σimages/BZ_81_1618_3096_1631_3141.pngr D第1排 0.013 0.000 1.659 0.276 –0.011 0.000 1.873 0.241 0.047 0.000 1.521 0.200第2排 0.064 0.000 1.428 0.427 0.072 0.000 1.882 0.241 0.226 0.000 1.442 0.212第3排 0.086 0.010 1.339 0.296 0.021 0.000 2.093 0.312 0.324 0.000 1.472 0.282

图3 本文模型与其他3种算法去雾效果对比

表2中的数据是对图3的客观评价，从表2中可以看出，文献[22]算法虽然产生了较小的雾感知密度D，但由于过饱和现象，使得去雾后变成白色的像素点增多，σ值偏大。本文算法相较于文献[18]和文献[21]算法虽然产生了几乎类似的平均可见度，但本文产生了最小的感知雾密度D以及较大的可见边缘e，整体而言，本文去除浓雾方面效果相对较好。

表2 图3中各算法定量比较(e、σ、r、D)

3.2.3 本文模型的适用性分析

为了测试本文模型的适用性，从 LIVE Image Defogging数据库中随机挑选了100幅有雾图像进行了实验。图4为ADMM方法与对偶方法求解能量方程所需要的平均用时直方图；图5和图6为各算法平均用时统计直方图及e、D去雾性能指标的统计直方图。从图4中可以看出，虽然ADMM求解能量方程的效率相比于对偶算法求解更加高效，但由于需要不断地迭代直到能量方程收敛，相比于其他算法，计算效率较低。从图6中可以看出本文算法相较于其他算法，具有较大的新增可见边之比e，说明本文算法纹理细节保持效果较好；图7中，文献[5]算法平均雾感知密度D最低，但新增可见边之比e较大，使得去雾后的图像过饱和并有曝光现象，图像边缘丢失。而本文算法的去雾浓度相对较低，说明本文算法去雾效果良好。

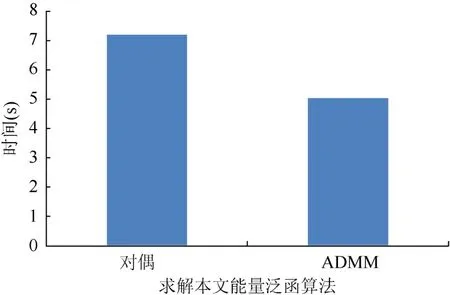
图4 ADMM算法与对偶算法100幅图片平均时间对比统计

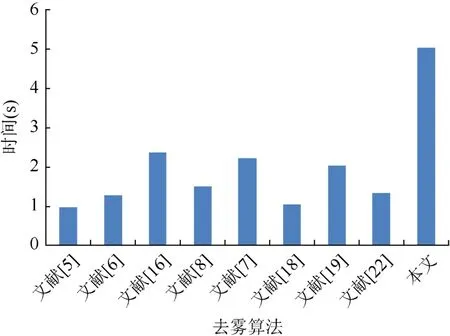
图5 本文与其他算法100幅图片平均时间对比统计

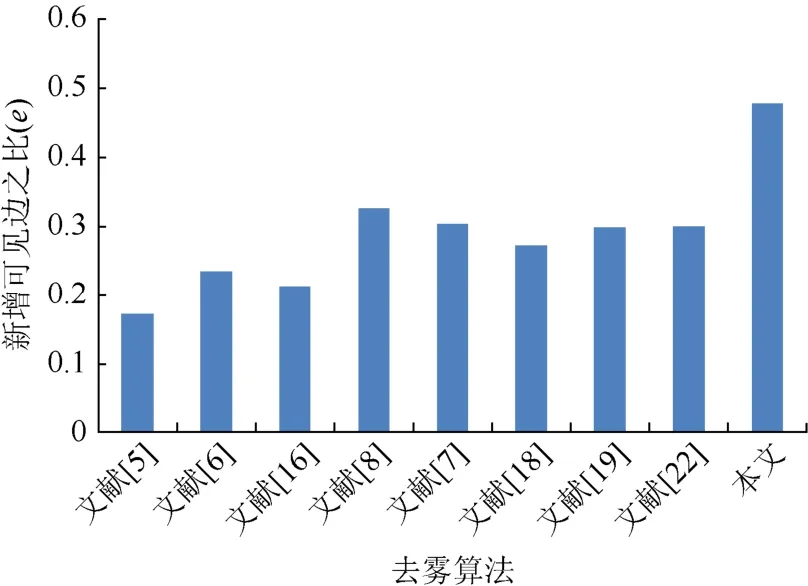
图6 本文与其他算法100幅图片平均新增可见边之比对比统计

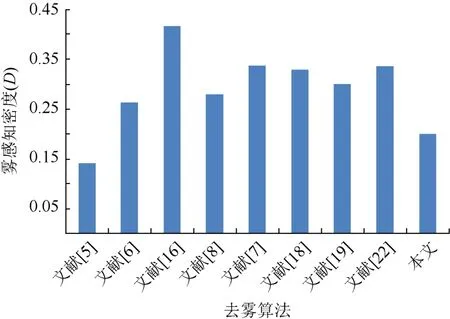
图7 本文与其他算法100幅图片平均雾感知密度对比统计

4 结 束 语

本文首先利用暗通道先验得到粗略的透射率图，然后提出了一个二阶变分去雾模型，并同时实现透射率图的精细化和去雾图像的恢复。引入Hessian正则项保留了透射率图和去雾图像的重要结构，提高了图像的对比度、可见度，设计了相应的ADMM算法，提高了模型的运算效率。最后实验结果表明，本文模型可以有效修复有雾图像，去雾后的图像清晰自然，纹理细节保持效果较好。但由于本文算法需要不断更新迭代拉格朗日乘子，直到能量方程收敛，虽然设计了相应的ADMM 算法提高计算效率，但仍然不能实时去雾，受深度学习Adadelta优化器具有较快收敛速度的启发，结合Adadelta算法提高运行速度是后续研究的方向。