智能车经济性起步车速规划研究*

金 辉，张 俊

（北京理工大学智能车辆研究所，北京 100081）

前言

智能车技术是当前的研究热点，《中国制造2025》明确指出，到2025年掌握自动驾驶总体技术和各项关键技术，综合能耗较常规汽车降低10%以上，减少排放20%以上［1］。因此在发展智能车技术过程中，实现起步工况的最优经济性起步车速，提高车辆行驶性能成为智能车的一项必要的基本功能。

瞬态油耗的估测在车辆燃油经济性评估中十分重要。对于经济性车速规划而言，车辆燃油消耗模型需要满足计算的准确性。通常研究者习惯于采用查发动机MAP图的方式获取稳态燃油消耗率，有研究者指出发动机稳态下的燃油数据比实际路况下的瞬态数据偏差达到6%～30%［2-3］。在过去20多年里，研究者们开发了多种燃油消耗模型，文献［4］中从模型输入的角度将模型分为了微观、中观和宏观3类。微观模型主要利用车辆瞬态参数如车速、加速度等来估算瞬态燃油消耗，也可以称为瞬态燃油消耗模型，代表性的有VT-Miro模型［5］和BIT-TFCM模型［6］；中观模型的输入主要是车辆在行驶过程中所经历加速、匀速、减速和怠速等不同模式，车辆燃油消耗等于所有模式之和，代表性的有Elemental模型［7］；宏观模型的输入一般是行驶时间、行驶距离和平均速度等参数，这是一种基于海量数据的地区性燃油消耗估算模型，如美国环保局在交通规划领域常用的MOBILE系列模型［8］。对于智能车的经济性车速规划而言，计算车辆瞬态下的燃油消耗率，是实现复杂规划算法的基础。微观燃油消耗模型显然更适合作为经济性车速规划算法的目标函数。

智能车具备良好的行驶性能是“智能”的重要特征之一。对于目前智能车车速规划，应用较多的是梯形车速规划［9］，该方法只给出了基本的安全要求，没有考虑车辆动力学特性和行驶性能要求。文献［10］和文献［11］中利用V2X技术等充分利用道路和交通约束信息来规划经济性车速，研究表明优化后的经济性车速能提升燃油消耗水平达34%；文献［12］和文献［13］中基于道路坡度信息计算经济车速，提高车辆对坡道环境的适应性；文献［14］中基于弯道信息规划从进入弯道到驶离弯道的经济性车速，采用优化后的车速比典型驾驶员过弯车速提升燃油消耗水平4.76%～14.61%。这些研究表明，基于行驶环境、行驶工况来优化车速可以显著提升燃油经济性。以往起步阶段的研究中以改善离合器接合品质、变速器换挡品质等为主［15-16］，属于局部性和功能性优化，起步阶段以燃油经济性为目标的车速规划研究目前还比较少见。

本文中以智能车起步过程燃油经济性为优化目标，从全局的角度优化起步阶段的车速和挡位序列。在瞬态燃油消耗模型的基础上，介绍了BIT-TFCM模型的数据标定及使用方法，并与真实燃油数据进行了比较；基于该模型，建立了经济性换挡规律设计方法。根据车辆平路动力学模型，给出了离散形式的车速状态转移方程；利用动态规划算法求解了智能车起步工况下的最优经济性车速和相应的挡位序列；最后通过Matlab／Simulink和CarSim联合仿真，验证了经济性车速的节油特性。

1 瞬态燃油经济性模型

1.1 BIT-TFCM模型

尽管目前国家在推行新能源汽车战略，但2018年全年汽车产量为2 780.9万辆，其中新能源车产量为127万辆，占比不到5%［17］，因此本文智能车选取燃油车作为研究对象，提高燃油型智能车的起步经济车速规划水平，具有现实应用意义。如前述，微观油耗模型更适合作为经济性车速规划的油耗估算模型。基于课题组研究基础，采用周敏等人提出的“稳态初估＋瞬态修正”BIT-TFCM燃油消耗模型［18］，该模型第1部分根据稳态工况下的发动机的转矩、转速插值计算稳态油耗值；第2部分根据车辆速度、加速度估算瞬态修正量，最后将两者组合得到最终的估算结果，其结构形式如下：

式中：ms为稳态下油耗，cm3／s，根据MAP图插值计算；mc为模型估测的实际油耗与稳态模块计算油耗的差值，cm3／s；mf为估算得到的油耗值，cm3／s。差值mc的计算方法如下：

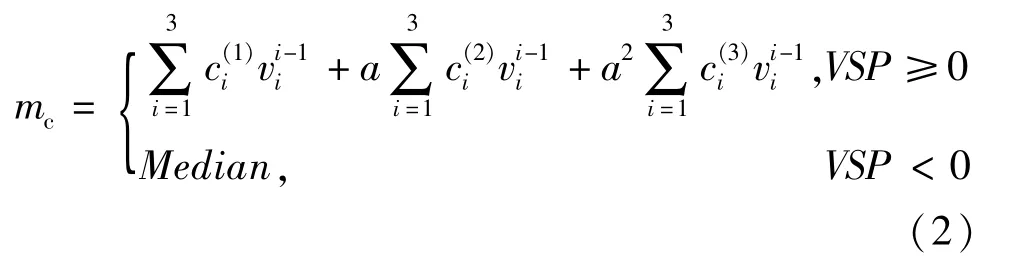
式中：Median为与车速v相关的值［15］，分别取v≤50 km／h和v＞50 km／h的燃油消耗率分布中值。

为说明油耗模型的标定过程，和后续研究车辆的特征，本文中根据美国阿贡国家实验室先进动力总成研究中心（the advanced powertrain research facility of argonne national laboratory，ANL）的D3数据库［19］，选用一款常见的2.0 L福特福克斯油耗数据作为标定基础，其基本参数见表1。

1.2 模型标定

油耗测量过程中由于测量设备、人为因素等原因不可避免地会产生误差，因此需要对数据进行预先处理。阿贡数据库原始数据的采样频率为10 Hz，为剔除毛刺使数据变得更平滑，本文中采用平均值滤波法，将采样频率降到1 Hz，其表达式为

表1 阿贡数据库的福特福克斯车型参数

车辆比功率（vehicle specific power，VSP）与车辆燃油消耗有很强的关联，为进一步剔除误差数据，本文中还采用VSP-3σ滤波方法，VSP最早是由Jimenez-Palacios于1999年提出，用于反映车辆的功率输出［20］，其表达式为

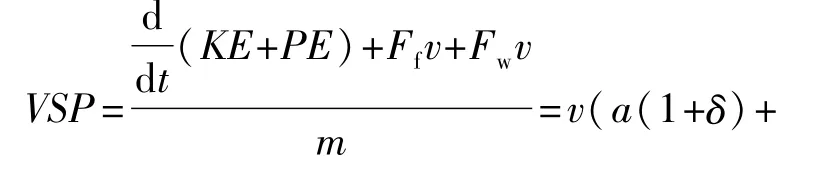
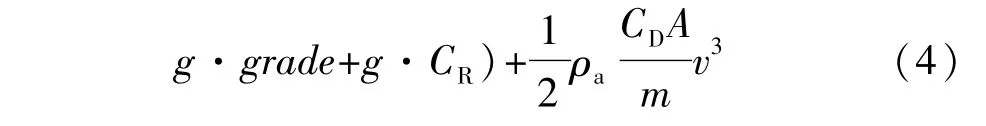
式中：KE和PE分别为车辆的动能和势能，J；Ff和Fw分别为车辆行驶滚动阻力和空气阻力，N；v为车速，m／s；a为加速度，m／s2；δ为车辆旋转质量换算系数；grade为道路坡度，%；g为重力加速度，9.81 m／s2；CR为滚动阻力系数；ρa为空气密度，kg／m3；VSP为比功率，kW／t。

然而实际交通环境中要实时获取式（4）的全部参数比较困难，为能够用传统的参数计算，Jimenez-Palacios对计算公式进行了简化，只需用车辆速度和加速度就能获取车辆的VSP值，其简化公式如下：

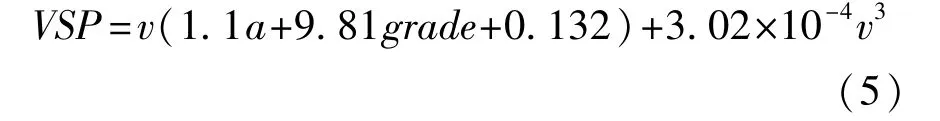
由于所测得的燃油消耗数据是在底盘测功机上获取的，因此式（5）的grade取0；在VSP的基础上，文献［21］中提出了VSP-3σ法数据预处理技术，将采集到的VSP数据分成若干个区间后，每个小区间的燃油消耗大致呈现正态分布，根据正态分布的特点，采样点落于±3σ之外的概率为0.002 6，因此属于小概率事件，可以考虑剔除。本文VSP区间取2 kW／t，绘制各区间的燃油值分布图，如图1所示。

根据上面平均值滤波方法和VSP滤波法，得到处理后的数据，如图2所示。对比分析可以看出，处理后的数据基本保留了数据的原始走势，并且毛刺得到有效的抑制。

下面根据阿贡数据库，对“稳态初估＋瞬态修正”燃油消耗模型进行标定，稳态模块使用“Steady State”数据进行标定；为兼顾高燃油消耗区和低燃油消耗区，动态模块采用数据库里提供的UDDS循环和US06循环的组合数据进行标定，标定数据段采用UDDS循环数据，测试数据段采用US06循环数据，模型测试结果如图3所示。

根据标定数据对式（2）进行标定，得到标定好的模型，对测试段进行验证，由图3可以看出，BITTFCM模型的计算结果准确跟踪了原始数据，能够满足作为后续油耗代价函数的准确性要求。

1.3 经济性换挡规律

最佳经济性换挡规律是指在保证车辆行驶驱动力的前提下，车辆经过连续换挡加速或者减速至某一车速时耗费的燃油量最小。在经济性换挡规律下，变速器提前升入高挡，从而使发动机处于负荷率比较高的工作状态，降低了燃油消耗，保证了燃油经济性。

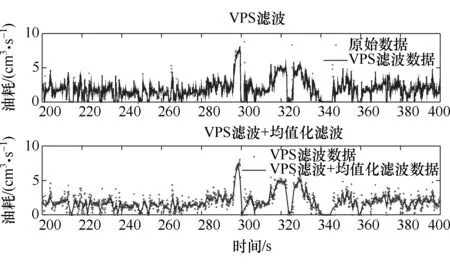
图2 数据滤波结果

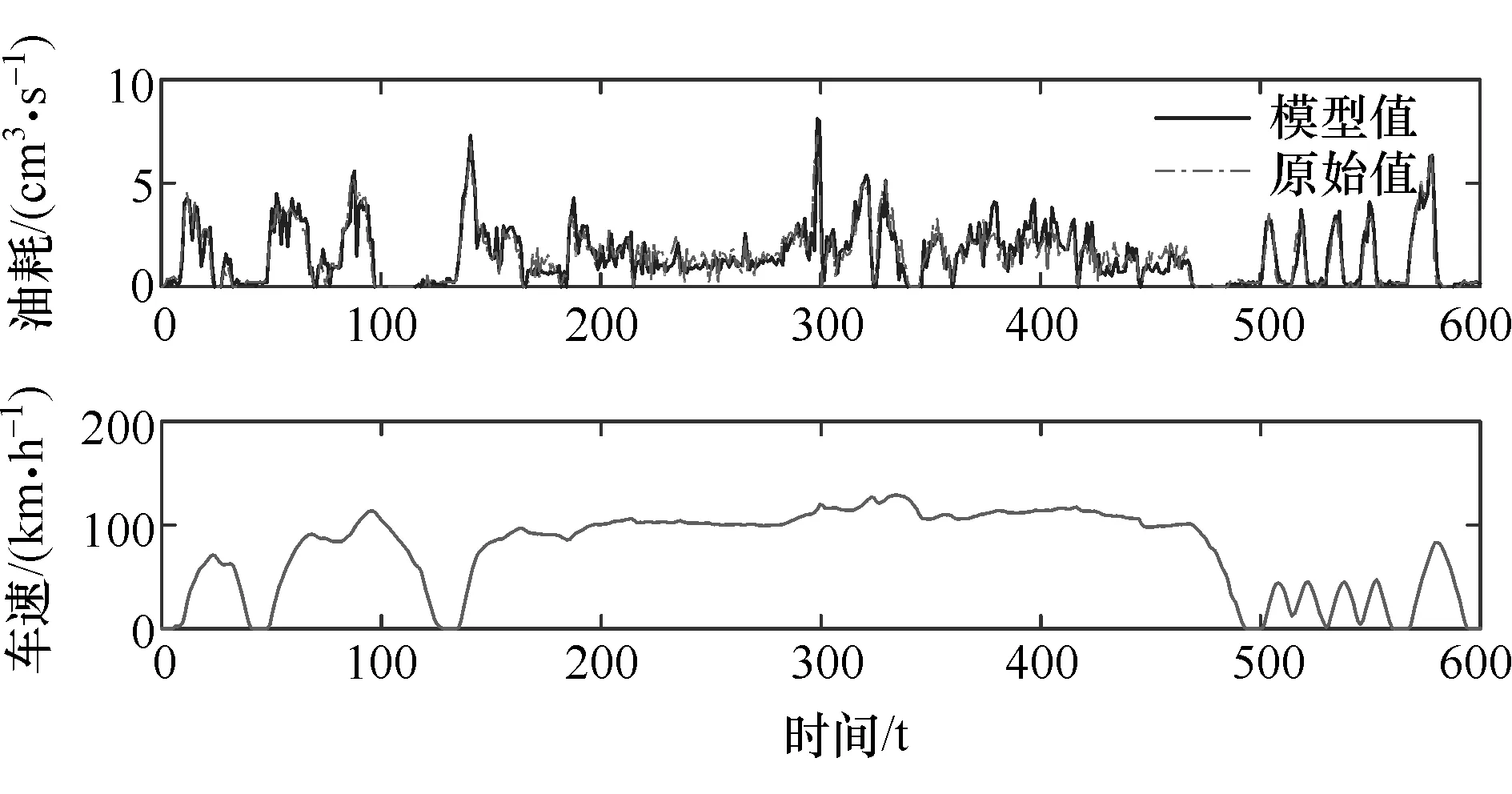
图3 瞬态油耗模型标定结果（US06循环）

经济性换挡规律的制定有多种方法，但大多都依赖于发动机燃油消耗值，以比油耗最小的不等驱动力换挡图解法为例，比油耗的定义如下：

式中：gea为比油耗，g／（kW·h）；GT为发动机小时油耗，g／h；Ft为车辆驱动力，kN；v为车速，m／s；Te为发动机转矩，N·m；ne为发动机转速，r／min；ηT为传动效率。然而这里的发动机小时油耗GT是依据稳态发动机万有特性表查询得到，实际行驶过程中，由于需要不可避免的加速、减速过程，实际情况发动机处于非稳态的工况更加常见，因此换挡规律采用稳态油耗值将会与实际偏差比较大，本文中采用BITTFCM瞬态油耗模型来制定经济性换挡规律。

为与标定好的福特福克斯油耗模型匹配，选用一款110 kW的发动机来制定换挡规律，其部分负荷特性如图4所示。

根据比油耗定义

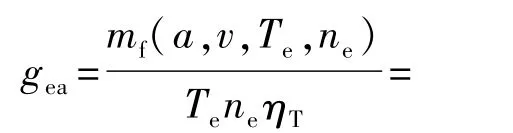
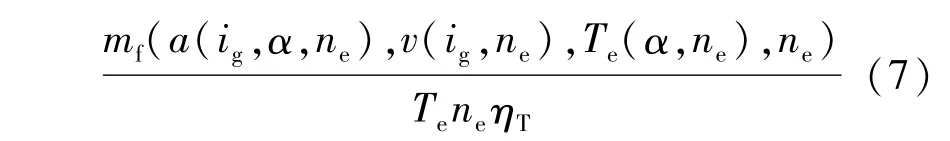
根据发动机合理的转速范围，可以绘制出各挡在确定节气门开度下的比油耗曲线，如图5所示，各挡曲线交点即为最佳燃油经济性换挡点。

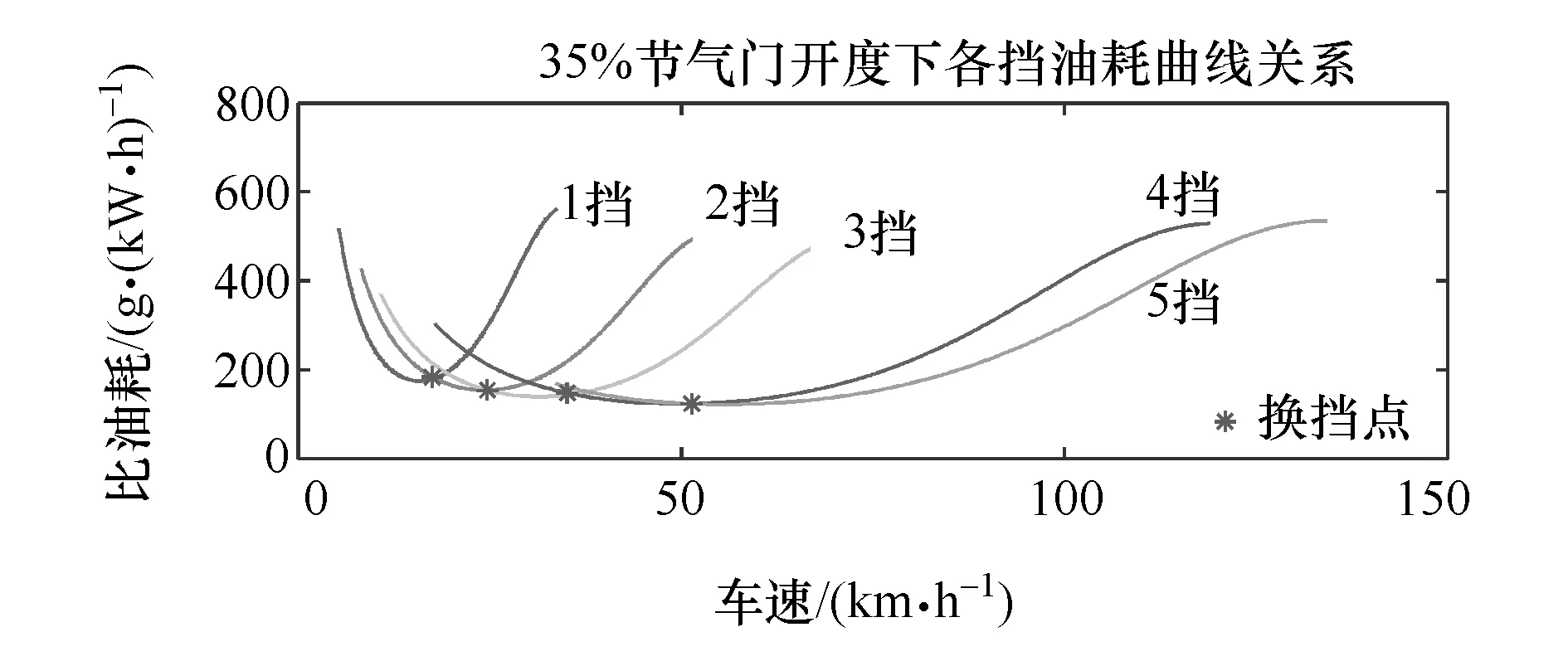
图5 35%节气门开度下各挡位换挡点

分别绘制各个节气门开度下的换挡曲线，得到的各个换挡点连接起来，得到升挡曲线，降挡曲线向左平移65 r／min（对应车速为2 km／h），绘制如图6升降挡曲线关系。

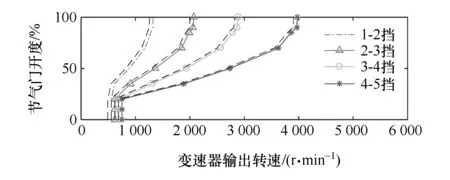
图6 基于瞬态油耗模型的经济性换挡规律

2 智能车起步经济性行驶模型

车辆在起步阶段，发动机输出的转矩经变速器、主减速器减速增转矩后，与车辆所受到的滚动阻力、空气阻力、坡道阻力、加速阻力相平衡。

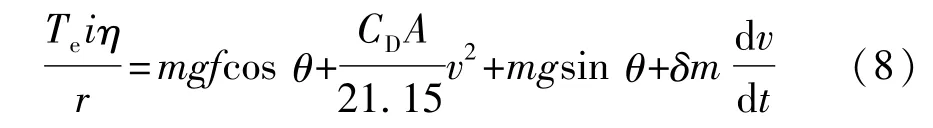
考虑平路条件下的起步工况，坡度θ＝0，并将式（8）速度单位统一为km／h，得到牛顿第二定律形式：

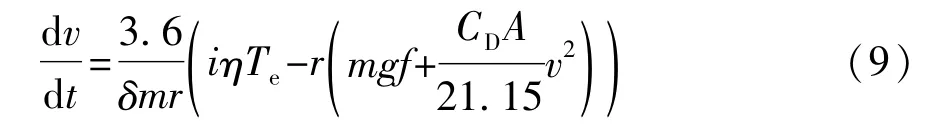
对于未来车联网条件下的经济性车速规划，智能车在精确电子地图的引导下按指定经济性车速行驶来获取最优燃油经济性，因此以行驶里程作为自变量信息显然要比行驶时间作为自变量信息更加合适，根据式（10）的变换关系：

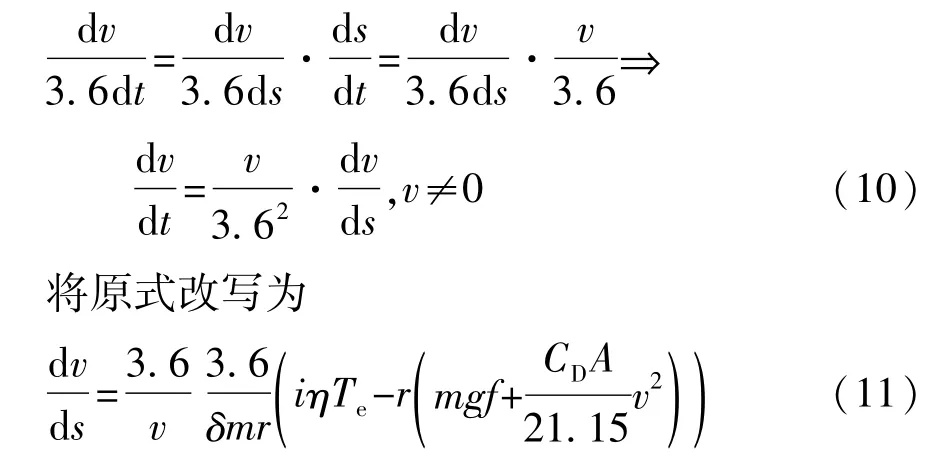
由式（11）可见，这是一个典型的非线性最优控制问题，车速v为系统状态变量，发动机转矩Te和总传动比i是控制输入量；平路采用恒定的经济性车速最节省油耗［10］，因此考虑终端速度为恒定值veco，根据丁峰等提出的稳态经济性车速制定方法［14］，智能车终端状态保持经济性车速veco＝49.8 km／h，初态速度设定为5 km／h，即离合器已完全接合。根据上述，系统的初始状态和终端状态都受到约束，即

对于式（11）这样强非线性方程，很难通过解析的形式得到最优解析解，因此考虑采用数值迭代的方法来求得最优离散解，这样也有利于处理挡位这样的非连续量。本文中采用前向欧拉离散方法对系统进行离散，得到的离散形式如下：

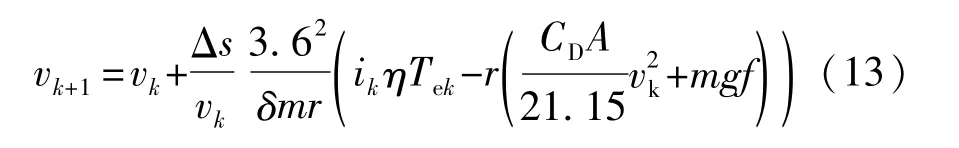
式中：vk＋1和vk分别为第k＋1阶段和第k阶段的速度，km／h；Δs为相邻两阶段之间的距离，m；ik为第k阶段的挡位速比，即挡位控制输入；Tek为第k阶段的发动机转矩输入，N·m。

系统的经济性最优控制问题转变为：在有限离散的位移段内，如何搜索最优的ik和Tek序列，使得全局燃油消耗最小。

以燃油经济性作为优化目标，采用前文标定好的动态油耗模型作为实时评估燃油消耗的代价函数，根据上文，可定义系统代价函数：

式中mf为车辆实时燃油消耗率。单个离散段的燃油消耗可写为

进一步，考虑到起步阶段的动力性和加速性能需求，在加速度约束条件中限制最小允许加速度值：

综合上面，得到起步阶段经济性优化模型式（18），包括系统状态转移方程、初末态约束、边界条件、代价函数方程等。

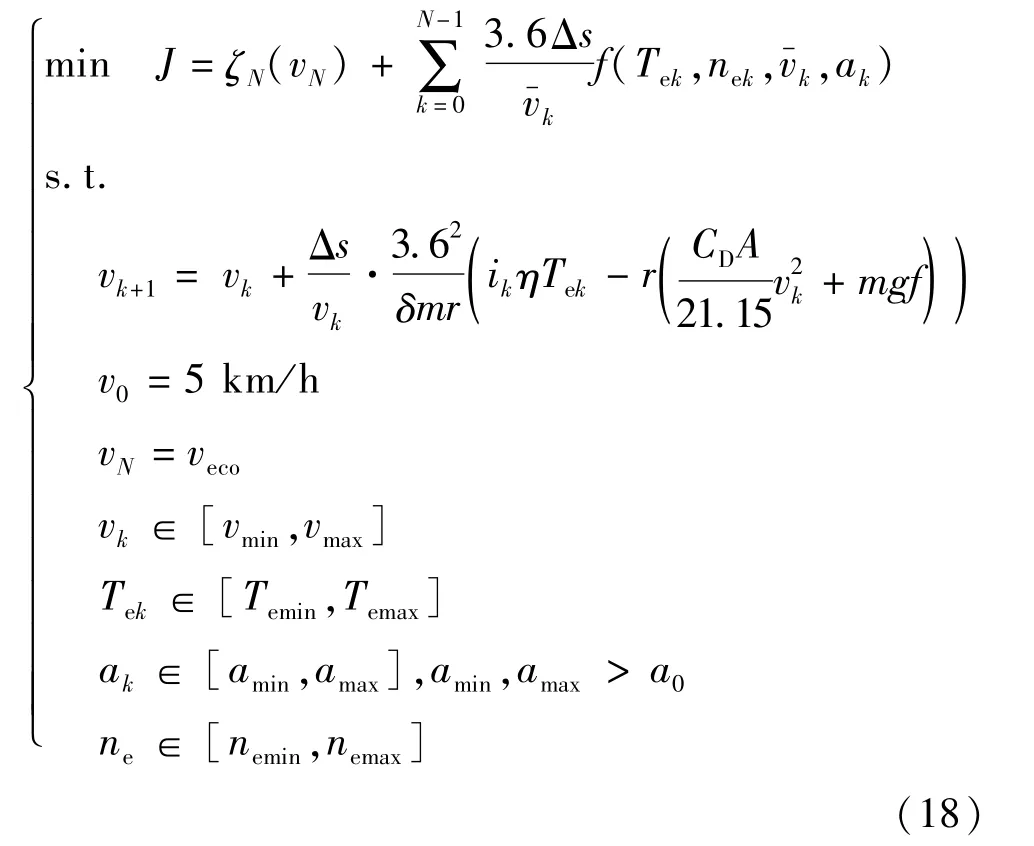
3 基于动态规划的求解策略

3.1 起步场景

假定智能车通过某150 m长的加速直道，道路全程无其他车辆干扰，行驶路况良好，要求智能车从5 km／h（离合器完全接合）加速到巡航经济性车速veco为49.8 km／h，通行全程发挥最大节油潜力，获得起步阶段良好的燃油经济性。

3.2 动态规划搜索原理

离散系统的最优控制问题是一个典型的多阶段最优决策问题，所谓多阶段决策，是指把整个过程按自变量分解成若干段，然后每段逐一做出“最优决策”，使得整个过程取得性能最优。Bellman动态规划（dynamic programming，DP）是解决多阶段最优决策问题的有力工具，其原理为最优性原理：一个最优决策应有这样的性质，不论初始状态和初始决策如何，其余决策对于由初始决策所形成的状态而言，也必定是最优策略，即一个最优策略的子策略也是最优的。本文中提出的起步最优速度规划方法基于动态规划最优性原理搜索。

为限制速度离散程度，将合理的速度区间［vmin，vmax］离散成M个速度点，全程位移离散成N个计算点，每个计算点对应于M个离散速度点，动态规划的寻优策略就是从每个位移离散点中寻找一个最优的速度点，构成N个速度序列，使得全局燃油消耗最小，同时这种最优的速度序列点的搜索过程受到约束条件的限制，具体搜索过程如图7和图8所示。

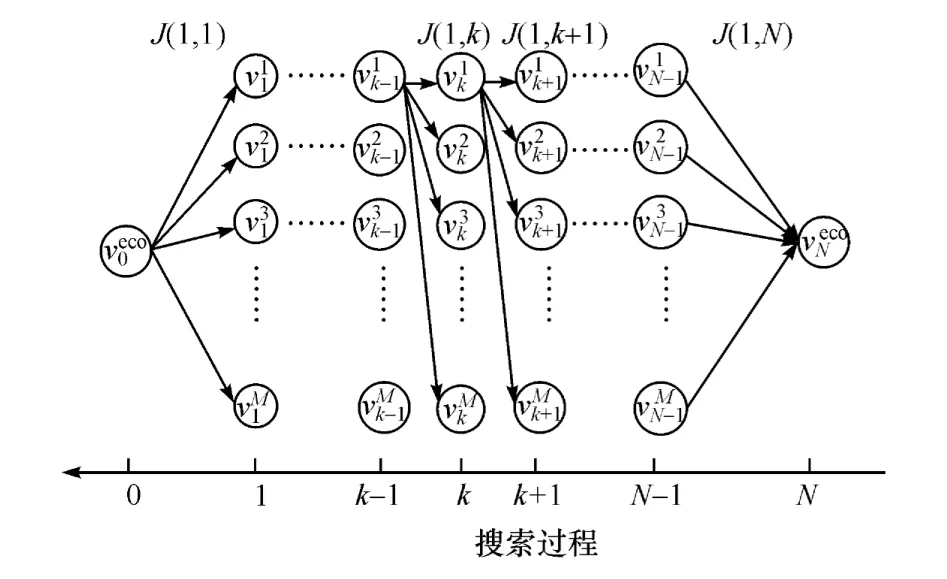
图7 动态规划搜索图

如图9所示，最终计算得到最优的经济性车速轨迹和挡位序列，可以看出在加速初期，算法根据全局提前升挡，以较长时间保持在4挡加速，在加速末端升到5挡，完成从起步到经济性车速的过渡，在略微降低加速效率的同时，使得发动机转矩输出保持在稳定区间，发动机工作点保持在高效区域，提升整个加速过程的燃油经济性水平。

4 结果验证

为验证算法计算的速度曲线和挡位序列具有良好的节油特性，建立了与典型驾驶员速度跟随模式的对比模型，并在Simulink和CarSim仿真平台进行。DP优化组通过PI算法控制节气门开度和制动踏板开度来跟踪已计算得到的最优速度轨迹和挡位序列；对照组通过简单驾驶员模型控制节气门开度和制动踏板开度来跟踪定速veco，挡位控制由CarSim内置的升降挡规律控制，仿真结构如图10和图11所示。

由图12可见，经DP优化的速度轨迹显著降低了燃油消耗，150 m的加速距离内，DP优化的起步模式较典型驾驶员速度跟随模式节油约9.37%；从通行效率看，表2的DP平均速度仅比对照组相差-3.18 km／h，几乎对通行效率影响不大，最优速度轨迹和挡位序列从理论上指导了经济起步的最优行驶策略，具体表现为以下特征：

①提前升入高挡，在保持加速性能的前提下取高挡来维持最优燃油经济性水平；

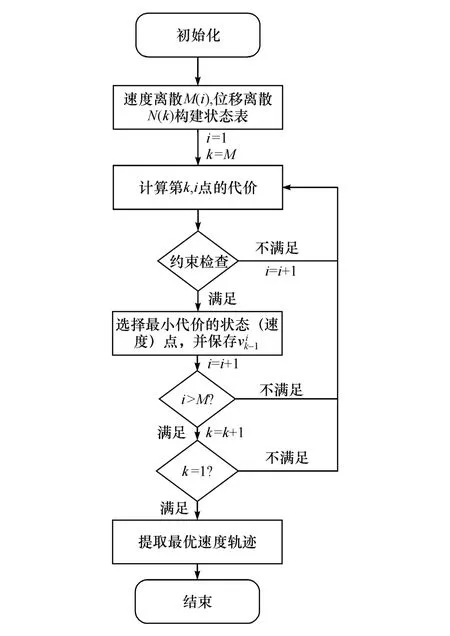
图8 动态规划算法搜索流程图

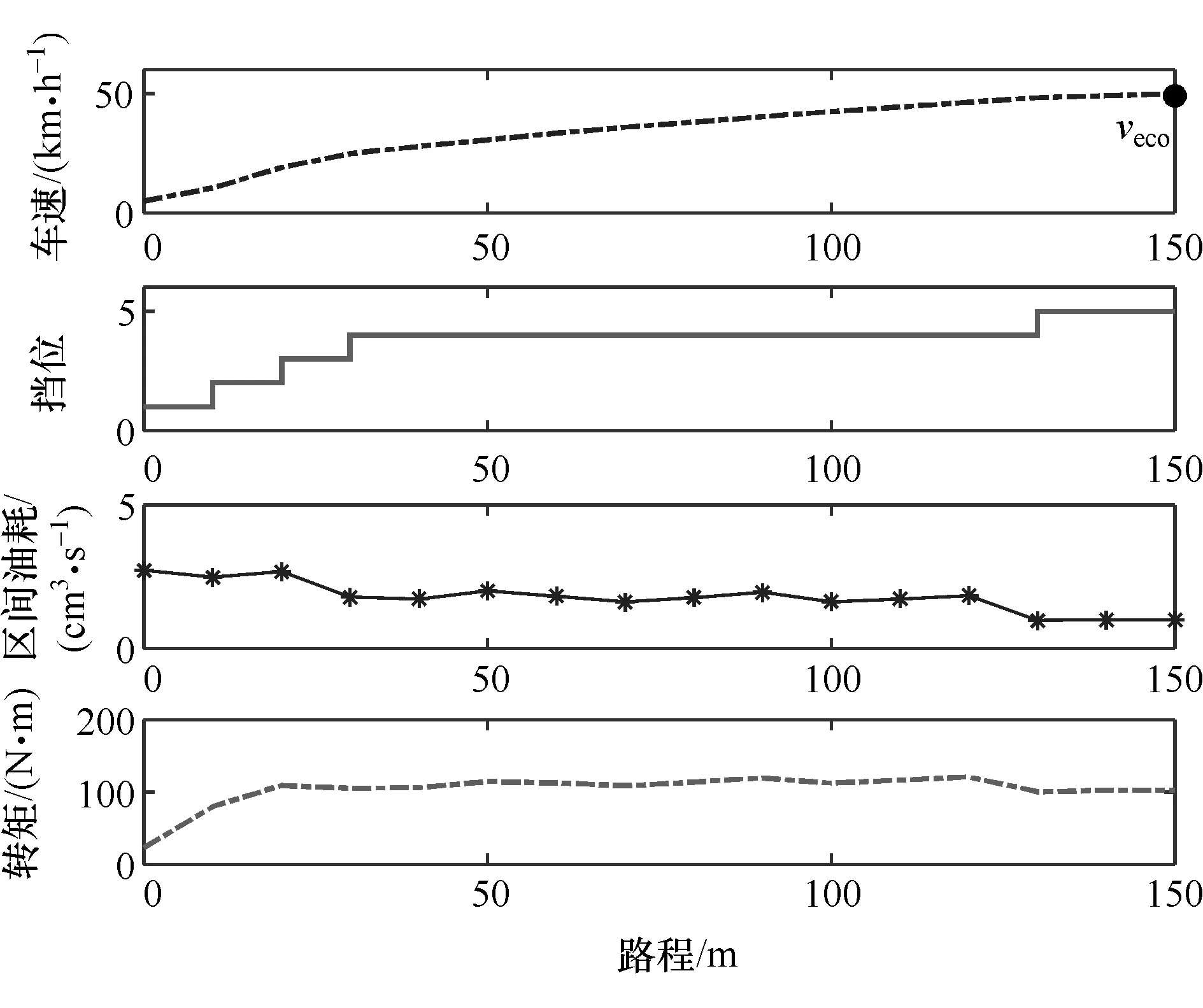
图9 150 m起步经济性车速规划结果

图11 仿真场景

②车速曲线尽量避免急加速，防止发动机功率突变；

③发动机尽可能保证均匀的功率输出，发动机转矩输出保持相对稳定水平；

④车辆驶离加速段时，保证末端经济性巡航车速和经济巡航挡位。

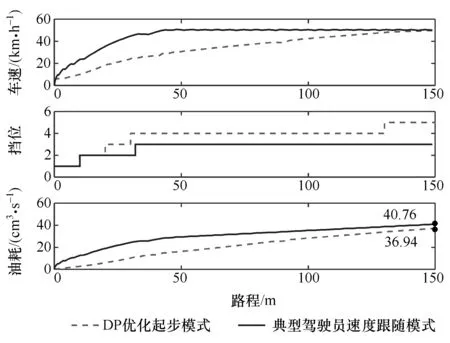
图12 仿真结果

表2 起步平均速度比较

5 结论

本文中根据美国阿贡国家实验室的实车燃油数据，建立瞬态油耗模型，并给出了模型标定方法，验证结果表明瞬态油耗模型具有较高的准确性；基于瞬态油耗模型制定了一种新的车辆经济性换挡规律方法；根据车辆起步条件，建立了基于速度的转移方程，确定了约束条件、边界条件和燃油消耗的代价函数；基于贝尔曼最优原理，利用动态规划的求解速度转移方程，获得了最优经济性车速及挡位序列，最后通过Matlab／Simulink和CarSim联合仿真验证了经济性车速的有效性。这项技术可以应用到无人车自主车速决策上，根据精确电子地图信息给出最优燃油经济性的速度轨迹及相应的挡位序列；也可以作为有人驾驶的车速指导，提升行驶过程的燃油经济性水平。