考虑稳健性的汽车结构耐撞性优化设计*
2020-03-18张海洋吕晓江周大永谷先广
张海洋,吕晓江,,周大永,夏 梁,谷先广
(1.浙江吉利汽车研究院有限公司,浙江省汽车安全技术研究重点实验室,杭州 311228;2.湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082; 3.合肥工业大学智能制造技术研究院,合肥 230009)
前言
随着计算机技术的不断进步和碰撞仿真精度的不断提高,有限元仿真与实车试验相结合的方法在汽车安全设计中得到了广泛应用[1-2]。然而,单次碰撞仿真通常需要消耗大量时间,对计算资源提出了较高的要求。而优化算法又是一个反复迭代的过程,在单次优化中需要调用大量的仿真结果来满足算法的迭代需求。为解决这一问题,需要建立一个能够代表实际碰撞过程的高精度近似模型。近年来,支持向量回归(support vector regression,SVR)模型以其能够有效拟合小样本、高维度、高度非线性试验数据的能力,引起了工程设计人员的广泛关注[3-4]。然而,由于SVR模型中存在大量不确定性参数,其不同的设定往往会极大程度地影响所构建模型的预测精度,因此对SVR模型的参数进行合理选择尤为重要。本文中使用粒子群算法(particle swarm optimization,PSO)对SVR模型的参数进行寻优,构建了基于粒子群算法优化的支持向量回归(PSO-SVR)模型,实现了对结构耐撞性响应的高精度预测。
近年来,稳健性优化设计方法由于具有能够有效地减小产品性能的波动、大幅提高系统稳健性的优点,逐渐被人们所重视[5-6]。本文中在确定性优化结果的基础上,将稳健性优化方法运用到该汽车的车身结构耐撞性优化问题中,并对不同的稳健度要求所获得的设计方案进行对比,最终获得了适用于工程实际的优化解。
使用基于PSO-SVR近似模型的稳健性优化方法,对某汽车进行40%偏置碰撞工况下的结构耐撞性优化设计。优化流程主要包括:最优拉丁超立方试验设计、PSO-SVR近似模型的构建及精度验证、非支配排序多目标遗传算法Ⅱ(NSGA-Ⅱ)迭代和稳健性优化设计。最后,将所获得的优化方案进行了仿真验证。结果表明:经过本文的稳健性优化设计后,整车的结构耐撞性得到提升,车身质量减轻,同时保证了稳定的产品性能。
1 汽车结构耐撞性问题描述
1.1 整车40%重叠度的偏置碰撞仿真建模与试验验证
为研究某车型在40%重叠度偏置碰撞工况下的结构耐撞性问题,建立了整车和可变形壁障的有限元模型。为检验该模型精度,将仿真结果与实车碰撞的试验结果进行比对,其车身变形示意图如图1所示。可以看出,二者车身变形部位和变形模式基本相同,运动姿态基本一致。
仿真与试验结果的车身B柱下方减速度曲线对比如图2所示。由图可知,两者车身B柱下方的减速度变化趋势基本吻合,峰值大致相等。根据工程经验可以判断,该仿真模型的精度较高,可以用于后续的结构耐撞性优化设计。
1.2 设计变量、优化目标与约束
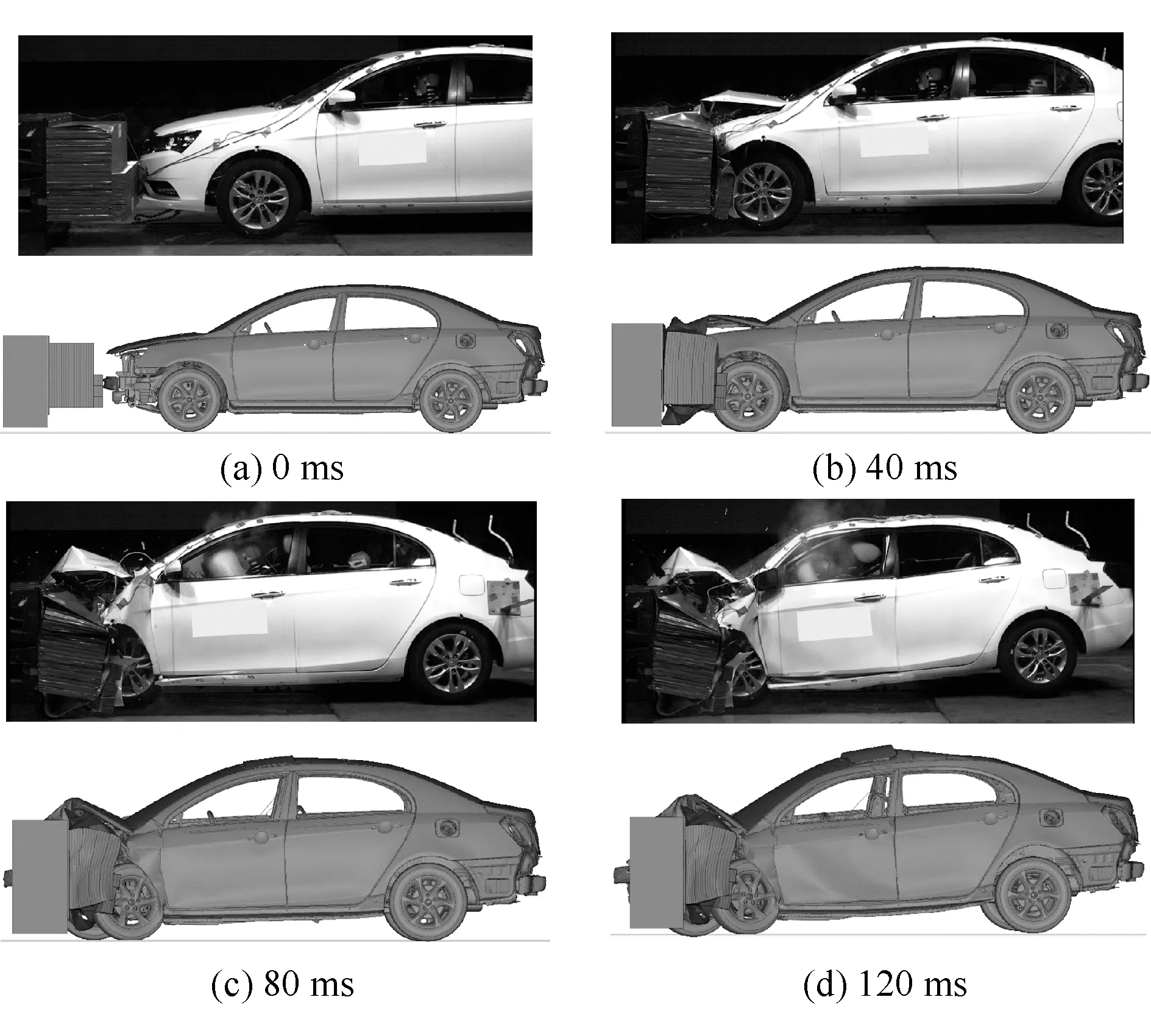
图1 仿真与试验结果的车身变形示意图
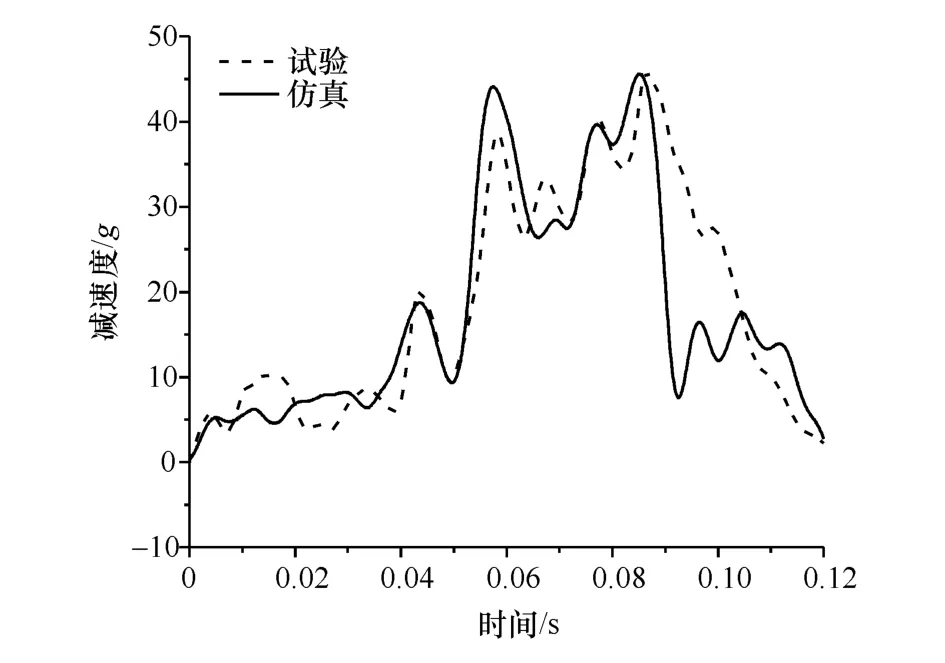
图2 车身B柱下方减速度对比
结构耐撞性输出响应的初始设计值和优化目标如表1所示。
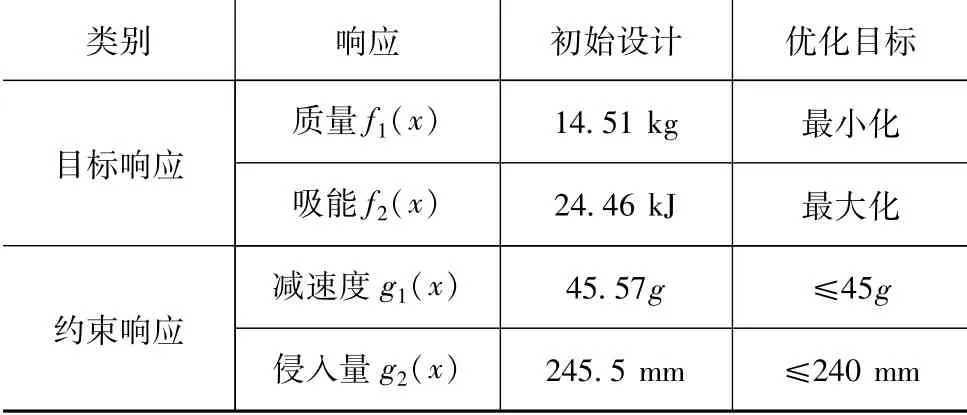
表1 输出响应与初始设计
为提高该车型的结构耐撞性,建立设定如图3所示的优化流程。以优化板件的总质量和吸能为目标、以B柱下方峰值减速度和防火墙侵入量为约束对该车型进行优化。
考虑到该车型前端结构中的各部件在偏置碰撞过程中的重要性,最终选取12个部件的板料厚度作为设计变量。由于结构的对称性,将其进一步简化为如图4所示的7个设计变量,用x1~x7表示,它们分别为前防撞梁外板、前防撞梁内板、吸能盒外板、吸能盒内板、中段前纵梁外板、后段前纵梁外板和前纵梁内板等7个待优化板件的厚度。同时,在考虑设计变量的不确定性时,假设7个设计变量均为正态分布,并根据典型的加工精度和装配误差,将设计变量的变异系数σ/μ(其中σ为标准差,μ为均值)设置为5%[7]。设计变量的初始值及概率分布如表2所示。
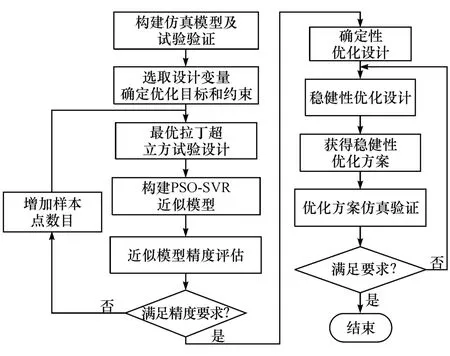
图3 汽车稳健性结构耐撞性优化设计流程图
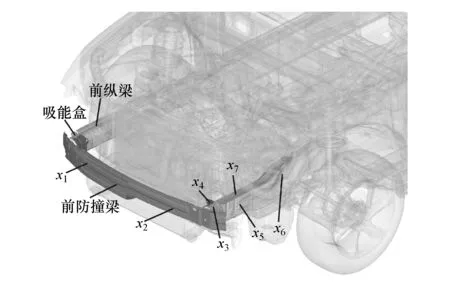
图4 设计变量示意图
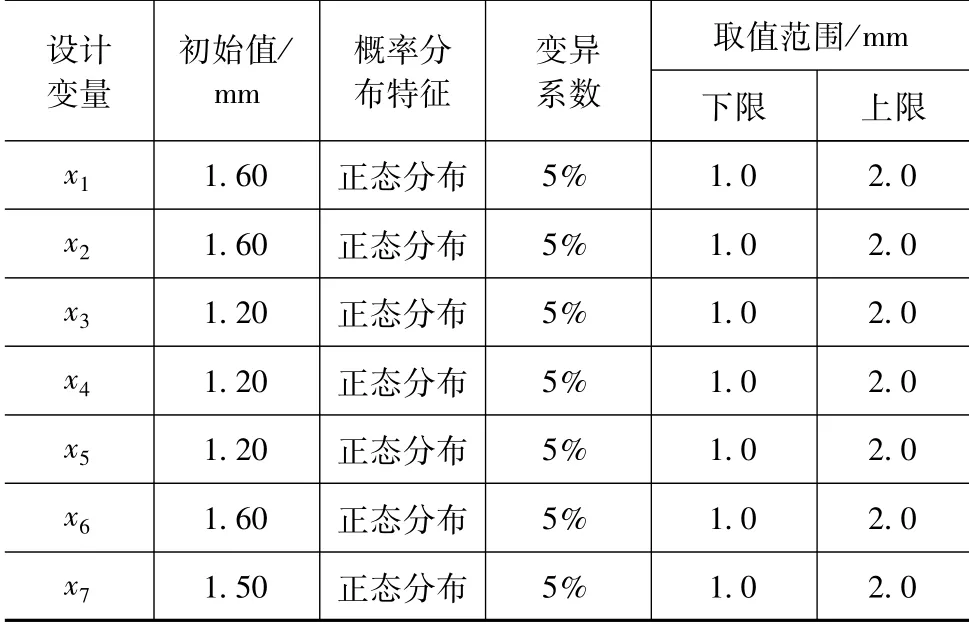
表2 设计变量初始值及概率分布
2 PSO-SVR近似模型的构建与验证
支持向量回归(SVR)模型是支持向量机在回归领域的拓展,其基本思想是寻找适当的预测函数,采用最大边缘准则将原始数据分为两类。当样本点数据线性不可分时,则必须使用核函数方法。核函数本质上是一种映射,当选择不同的核函数时,样本数据将被映射到不同的空间,SVR模型的预测值也不尽相同。此时,支持向量回归模型[8]的形式为
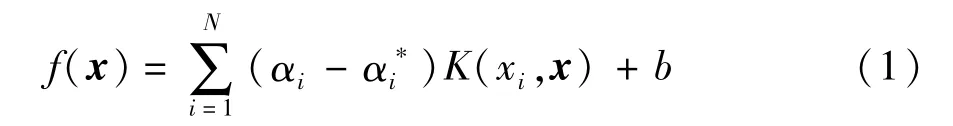
式中:K(xi,x)为核函数;N为样本点的数目;αi和为针对不同约束条件的拉格朗日乘子;b为阈值。根据结构风险最小化法则,求解函数f(x)可转化为以下的最优化问题[9]:
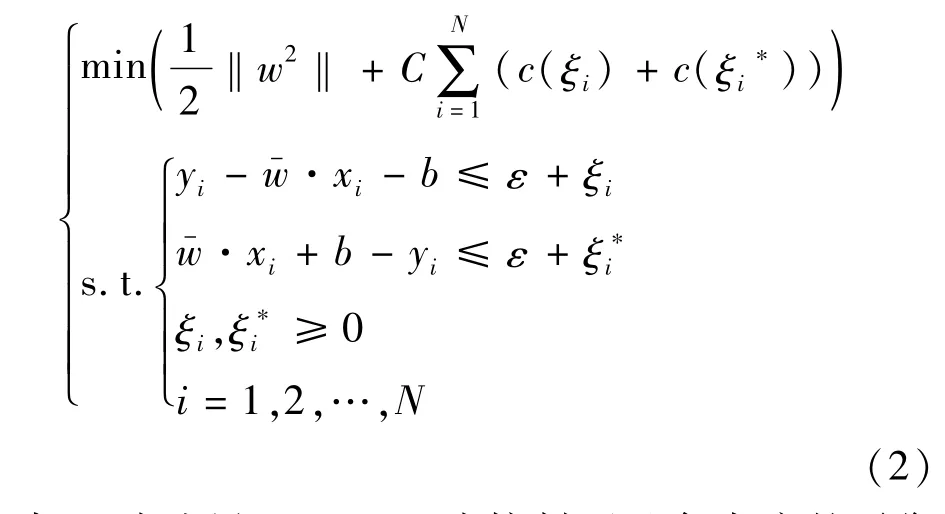
式中:w为边界且w>0;C为控制f(x)复杂度的平衡因子;c(ξi)和c(ξi*)为损失函数;yi为训练SVR模型样本点的响应值;ξi和ξi*为松弛因子;ε为不敏感损失函数的参数。
在SVR模型中,有多种类型核函数供选择,使用不同的核函数所构建的SVR模型,预测精度差异较大,典型的核函数类型见表3。
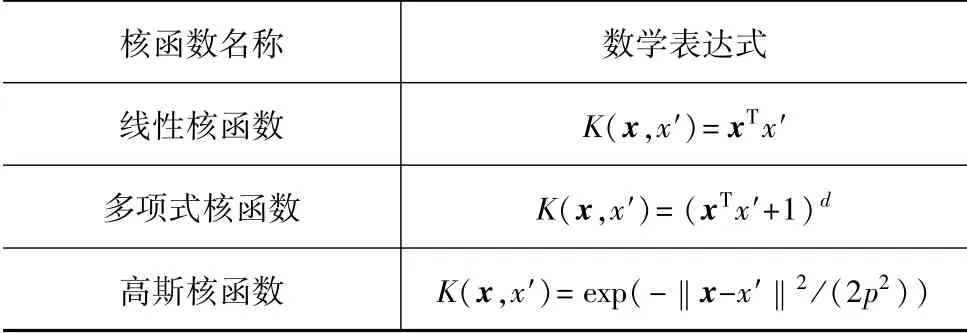
表3 不同类型的核函数
对于非线性问题而言,通常选用表3中的高斯核函数[3],因此本文选用高斯核函数作为SVR模型的核函数。SVR模型参数和核函数参数通常根据工程经验或经过反复测试获得,因此很难确定一个合理的取值。而粒子群算法[10](PSO)可以通过群体间、粒子间的合作与竞争进行全局优化搜索,能有效对SVR模型的参数进行选择。本文中利用PSO对SVR模型的平衡因子C、不敏感损失函数参数ε、高斯核函数参数p进行寻优,从而构建了适用于高度非线性的碰撞问题的PSO-SVR近似模型,SVR模型的寻优参数及其取值范围如表4所示。
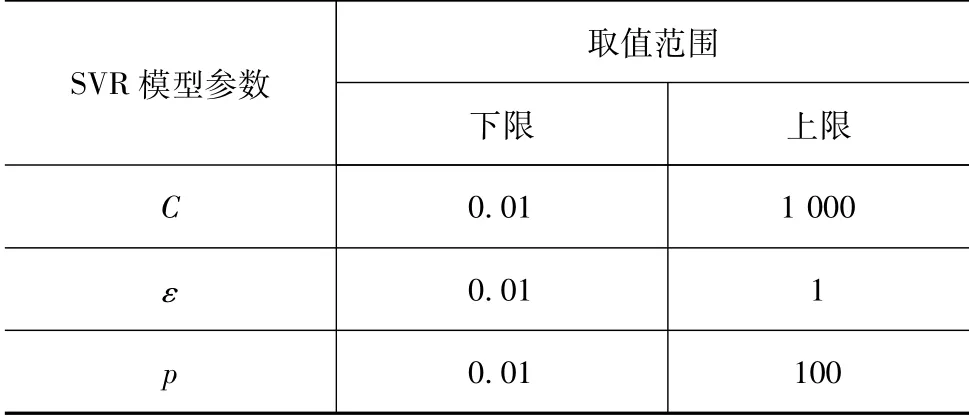
表4 SVR模型参数及取值范围
本文中PSO-SVR模型的参数寻优表达式为
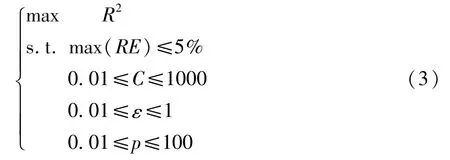
PSO-SVR近似模型构建完成后,使用最大相对误差max(RE)和决定系数R2对其精度进行评价[11]。其数学表达式可写为
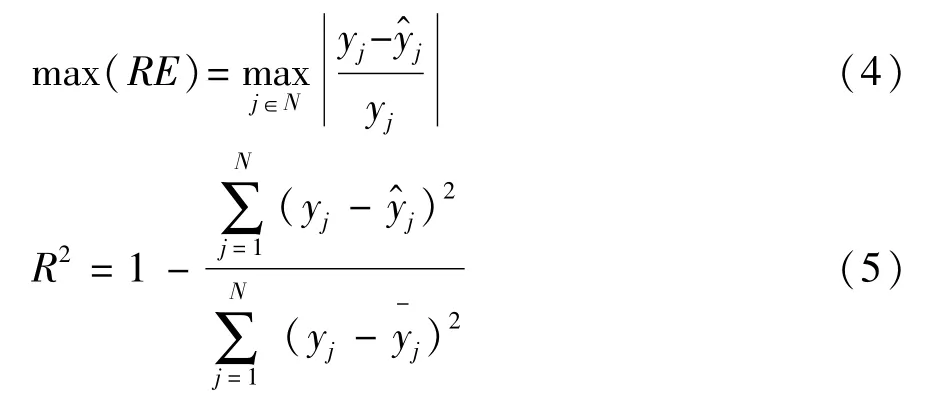
式中:yj为样本点的实际响应值;为PSO-SVR模型的预测值;为实际响应值的平均值。需要指出的是,R2的取值范围是[0,1],max(RE)越小,且R2越接近于1,表明所建立的PSO-SVR模型精度越高。
在汽车结构耐撞性优化中质量与板厚之间是线性关系,故选用线性核函数构建质量响应的SVR模型;对于总吸能、减速度和侵入量3个非线性响应,利用样本点数据分别构建克里金KRG、径向基函数RBF和PSO-SVR近似模型,并对其进行精度评估来比较不同近似模型对这些非线性响应的拟合效果。
近似模型的精度检验结果如表5所示。PSO-SVR模型构建的非线性响应的max(RE)值均低于KRG、RBF模型,R2值均高于KRG、RBF模型且满足R2≥0.9的要求。因此,所建立的PSO-SVR近似模型具有较高的精度,能够有效用于后续的优化设计流程。
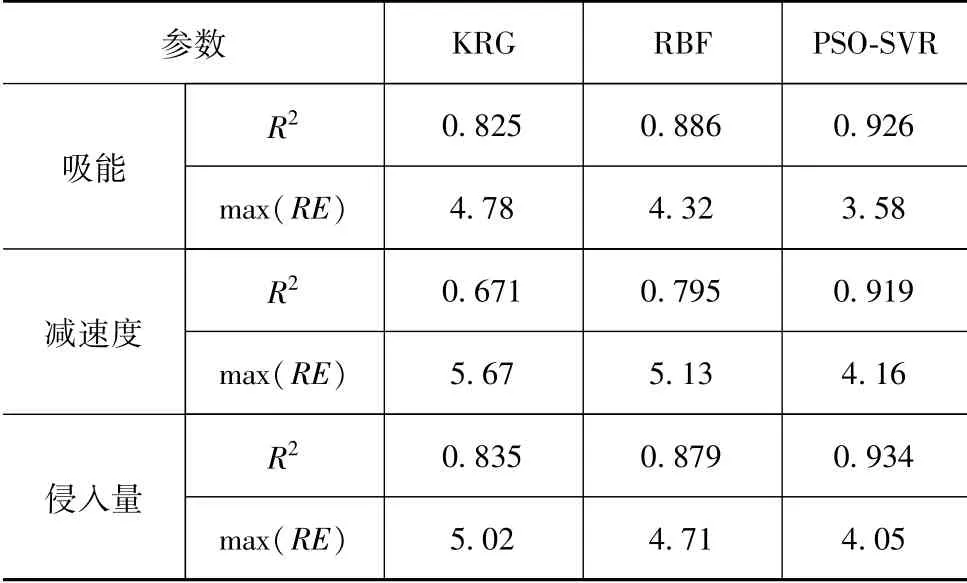
表5 近似模型精度检验结果
3 优化过程与结果分析
3.1 确定性优化
该问题的确定性优化的数学表达式为
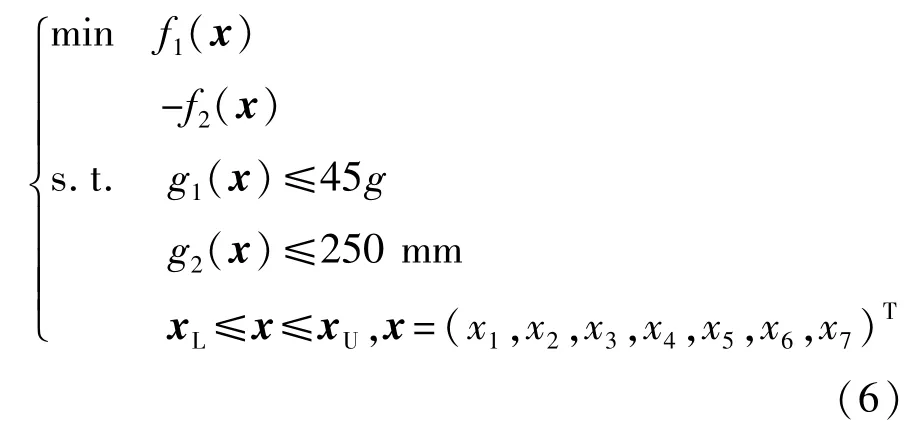
式中:f1(x)为优化板件的总质量;f2(x)为优化板件总吸能;g1(x)为B柱峰值减速度;g2(x)为防火墙侵入量。
使用NSGA-Ⅱ来获取该问题的Pareto前沿。NSGA-Ⅱ已被证明是一种搜索范围广、收敛性强的多目标优化算法,在工程问题中得到了广泛应用[12]。NSGA-Ⅱ的参数设置如表6所示。
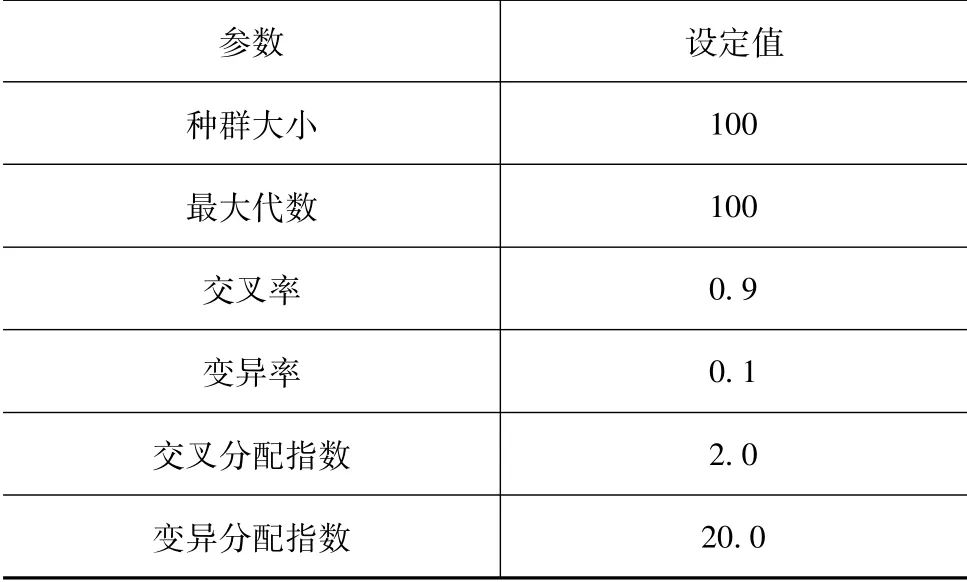
表6 NSGA-Ⅱ参数设置
确定性优化的Pareto前沿如图5所示。从图中可以看出,减轻质量和提高吸能这两个优化目标相互矛盾,即当质量增加时,吸能也随之增加,反之亦然。即两个优化目标不能同时取得最优解,只能从Pareto前沿非劣解中选取一个折中优化解。本文中采用最小距离选解法[13]进行选解,得到的优化结果见表7。从确定性优化结果来看,设计变量的总质量减轻了1.76 kg,汽车碰撞总吸能增加了0.87 kJ,同时B柱下方的峰值减速度和防火墙侵入量均满足设计要求。
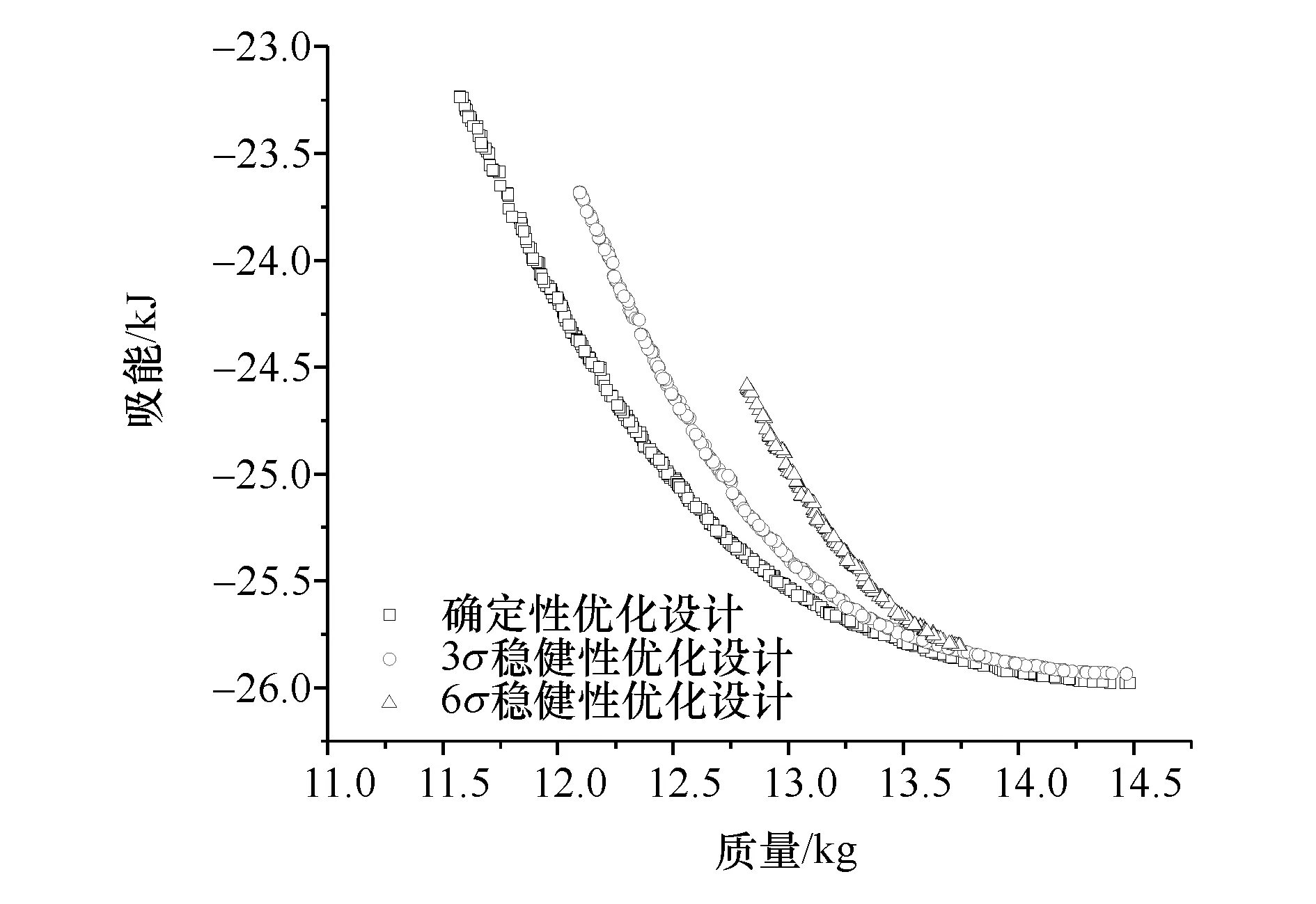
图5 确定性优化和稳健性优化的Pareto前沿
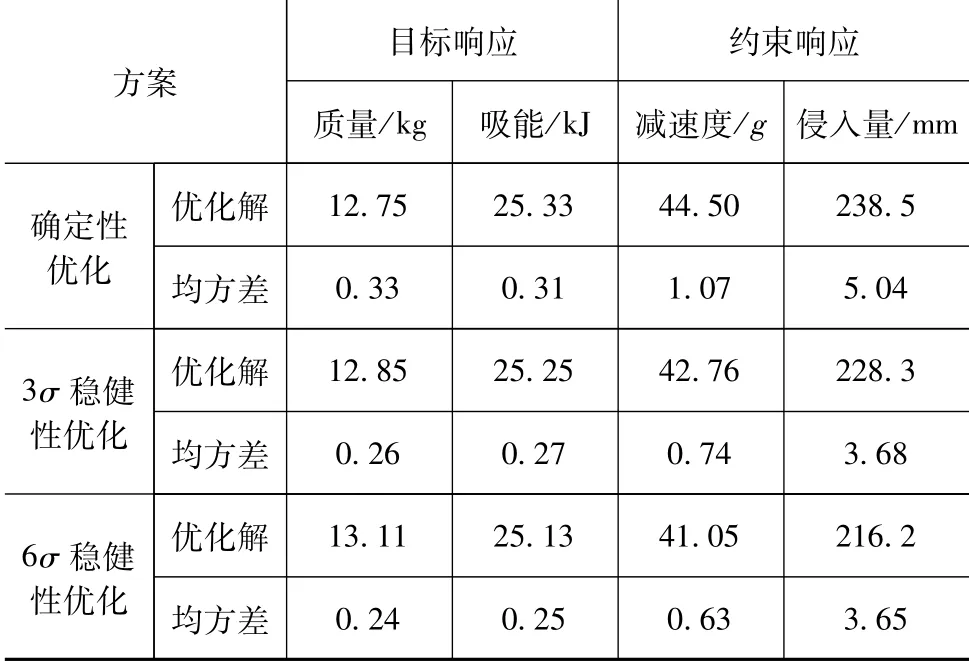
表7 确定性优化和稳健性优化设计方案
3.2 稳健性优化
由于生产工艺水平的限制,汽车零件的尺寸会存在一定波动,导致产品的性能产生一定偏差。由于确定性优化过程中未考虑任何不确定性因素,致使输出响应在这些因素的干扰下稳健度较低,故需要进一步进行稳健性优化设计。
该问题稳健性优化的数学表达式为
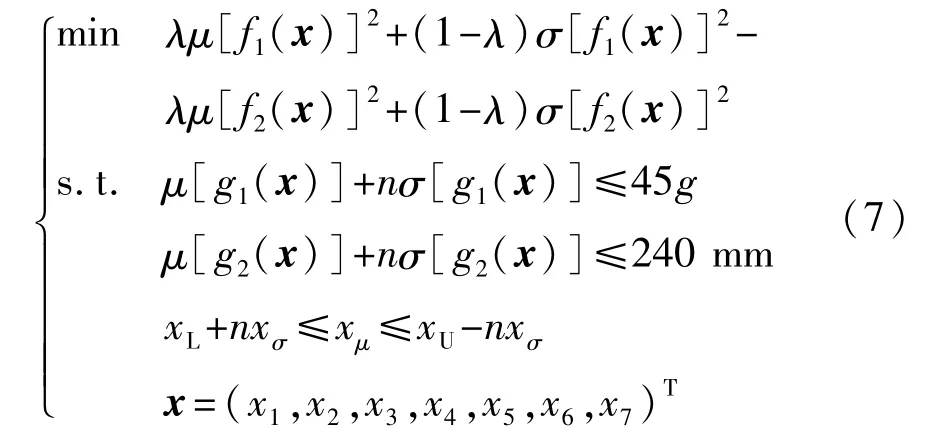
式中:λ为权重系数;n为稳健性评估指标;xL、xU、xσ和xμ分别为设计变量下限、上限、标准差和均值。
为评估不同的稳健度要求对优化结果的影响,将稳健性评估指标n依次设置为3和6,即分别对该系统实施3σ和6σ稳健性优化设计。同时,为较好地平衡均值和均方差之间的权重,选择λ=0.5作为式(7)中的权重系数。本文中使用蒙特卡洛描述性采样方法[11],将采集到的样本点带入所建立的高精度的PSO-SVR模型中进行稳健性优化。
图5示出不同稳健度要求下的Pareto前沿,随着稳健度要求的提高,所得到的Pareto解集趋向于远离确定性优化的Pareto解集,因而稳健性优化解在优化目标上略有下降。稳健性优化设计方案如表7所示,随着稳健度要求提高,优化目标和约束函数的均方差不断减小,系统的稳健度得以保障。与确定性优化相比,稳健性优化虽在优化目标上略有下降,但其系统稳健度却大大提高,更加适用于工程实际。
经过对不同的稳健性优化方案进行评估,最终选择6σ稳健性优化解作为优化方案,其对应的设计变量优化结果如表8所示。
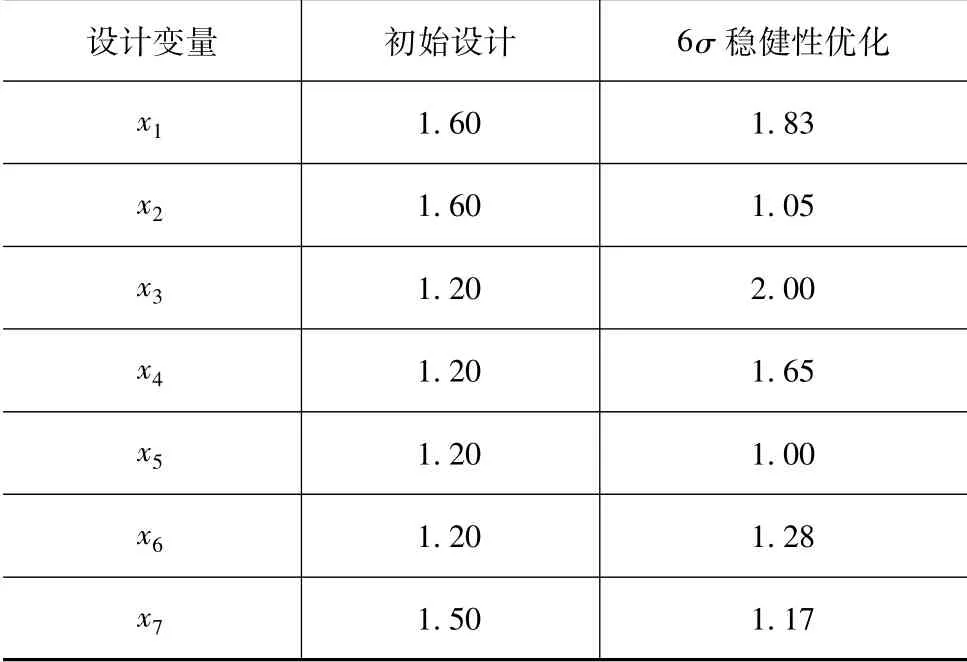
表8 优化设计变量取值 mm
3.3 优化结果的仿真验证
优化过程使用PSO-SVR模型代替了有限元仿真,因此需要将优化结果进行仿真验证。优化值与仿真值对比如表9所示。从仿真结果来看,优化后,质量减轻了1.35 kg,吸能增加了0.98 kJ,同时减速度和侵入量分别减少了3.3g和21.4 mm,优化效果明显。从相对误差来看,仿真结果与PSO-SVR模型预测值的最大误差仅为3.53%,表明本文所建立的PSO-SVR模型具有较高的预测精度。
图6为优化前后优化设计板件的吸能情况对比。可以看出,优化后吸能量优于初始设计。图7为优化前后的车身减速度曲线对比。可以看出,虽然两条曲线的变化趋势大体相同,但由于优化后吸能的增加,使其减速度峰值小于初始设计。
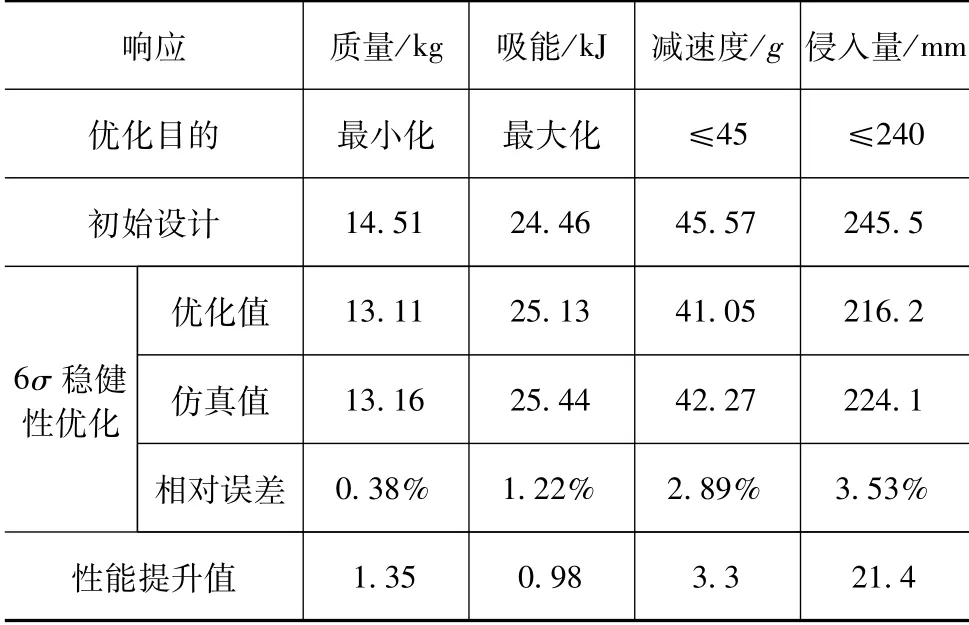
表9 优化与仿真结果对比
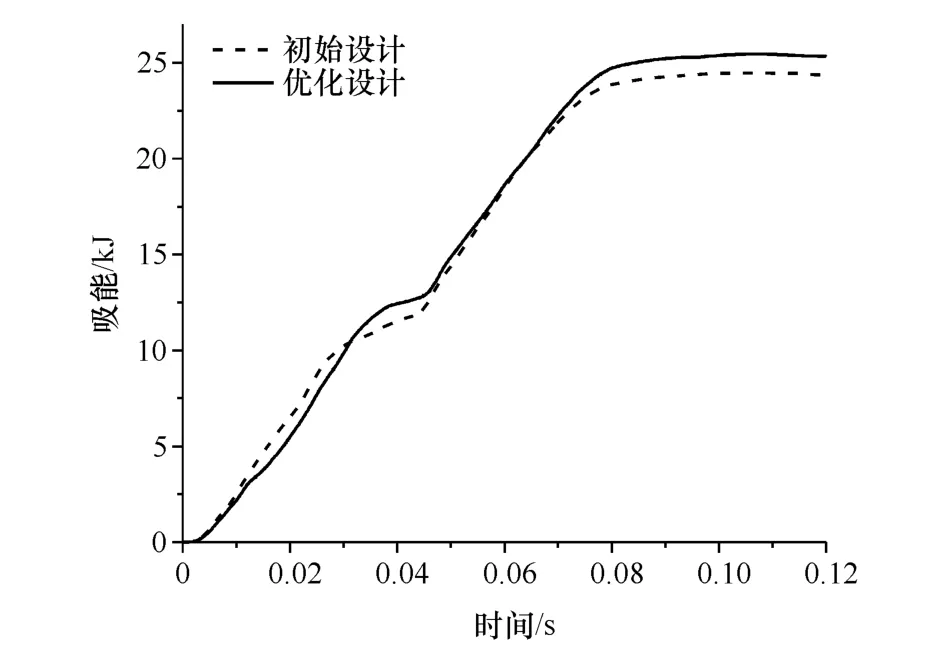
图6 板件优化前后吸能曲线对比
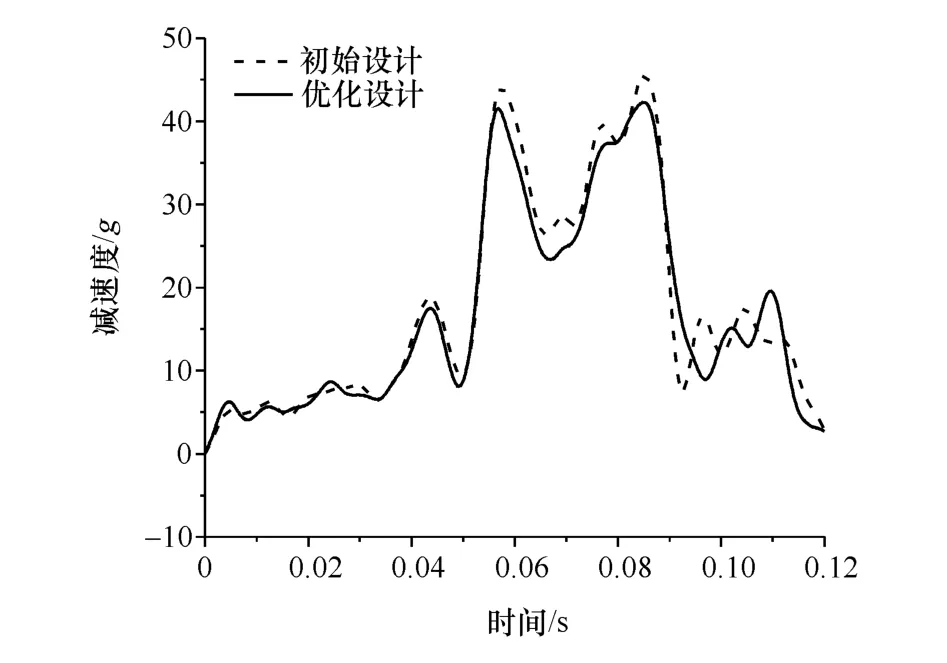
图7 优化前后车身B柱下方减速度曲线对比
图8为优化前后碰撞侧左纵梁的变形模式和防火墙侵入量对比。从图中可以看出,由于关键件厚度的合理搭配,优化后的左纵梁结构产生了更大幅度的渐进压溃变形,这种变形模式更有利于吸收能量和保持碰撞过程中的稳定,防火墙侵入量的最大值也减小了21.4 mm。总之,采用本文提出的优化方案,可以在减轻整车质量的同时提高汽车的结构耐撞性,同时保障系统的稳健性。
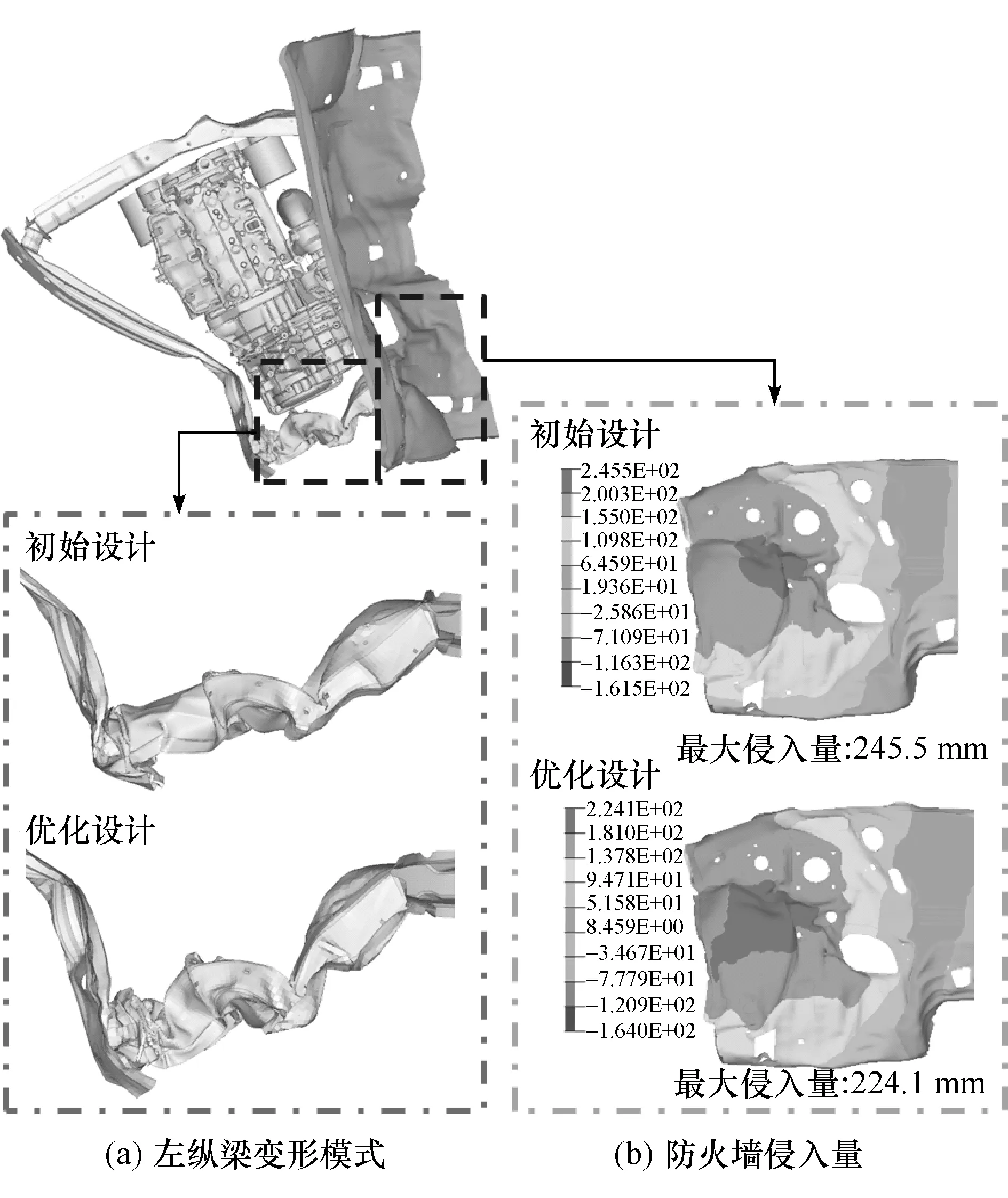
图8 优化前后左纵梁变形和防火墙侵入量对比
4 结论
(1)通过使用粒子群算法能够获得具有较高预测精度的PSO-SVR近似模型,适用于解决高度非线性的碰撞优化问题。
(2)确定性优化能够得到满足设计要求的优化解。然而,该优化解不能保障系统的稳健度,需要在其基础上进一步实施稳健性优化设计。通过稳健性优化设计,虽然优化目标的性能略有下降,但产品的稳健性得到了有效保障。
(3)稳健性优化方案不仅提高了该汽车的碰撞安全性与轻量化程度,同时保障了设计的稳健度。因而,相比于确定性优化设计,稳健性优化设计更加适用于工程实际。
