基准刑调节方法实证研究

●文 姬

量刑方法，包括量刑情节的区分和适用方法、基准刑的确定方法、基准刑调节方法。其中基准刑调节方法是量刑情节调节基准刑的方法。基准刑调节方法是量刑方法的重要组成部分。基准刑调节方法又包括两个部分，即量刑情节调节基准刑的调节程式（简称“调节程式”）和量刑情节调节基准刑的调节幅度模式（简称“调节幅度模式”）。在我国，基准刑调节方法包括两个方面的争议：一是调节程式上有 “复合模式”和 “单一模式”的争议；二是调节幅度模式上有“比例固定”模式和“数值固定”模式的争议。要解决这两方面的争议，需要依据实证资料进行研究。本文将利用盗窃罪的实证数据，探讨基准刑调节方法的上述两个争议。

一、基准刑调节方法的争议

我国《关于常见犯罪的量刑指导意见》（简称《量刑指导意见》）对于明确量刑步骤，建立相对独立的量刑程序，增强控辩双方关于量刑的有效对抗，强调刑事政策和量刑原则对量刑的指导，细化和规范量刑情节的辨识和适用，构建科学、规范的量刑方法等，起到了重要的作用。〔1〕参见石经海：《中国量刑规范化之十年检讨与展望》，载《法律科学》2015年第4期；黄晓云：《量刑规范化改革在实践中前行——访最高人民法院刑三庭庭长戴长林》，载《中国审判新闻月刊》2011年第68期。但是，对于基准刑调节方法中，调节程式为什么采取复合模式，以及调节幅度模式为什么采用“比例固定”模式，《量刑指导意见》及相关司法解释并没有给出具体的理由，因而引起了刑法理论界和实务界的争议。

（一）两种调节程式的争议

1.《量刑指导意见》中的调节程式：复合模式

我国《量刑指导意见》中的调节程式是复合模式。复合模式包含两个方面：一是，对于一般量刑情节，采取“同向相加、逆向相减”的调节程式，用数学公式可表示为，基准刑×（1+从重情节的调节比例-从轻情节的调节比例）；二是，对于特定的量刑情节（如未成年人犯罪、限制行为能力的精神病人犯罪、又聋又哑的人或者盲人犯罪、防卫过当、避险过当、犯罪预备、犯罪未遂、犯罪中止、从犯、胁从犯和教唆犯等“修正量刑情节”），则采取“部分连乘、部分相加减”的调节程式，用数学公式可表示为，基准刑×（1-修正量刑情节1的调节比例）×……×（1-修正量刑情节n的调节比例）×（1+从重情节的调节比例-从轻情节的调节比例）。〔2〕参见南英主编、戴长林副主编、最高人民法院刑事审判第三庭编著：《量刑规范化实务手册》，法律出版社2014年版，第32-35页。笔者将复合模式定义为两种调节程式相结合的量刑方法，而单一模式定义为只采取一种调节程式的量刑方法。这一定义与引文中的论述稍微有所区别。

与复合模式相对应的是单一模式。单一模式是指，不管对于一般量刑情节还是对于“修正量刑情节”，均采取“同向相加、逆向相减”的调节程式。

可见，复合模式和单一模式的区别在于，对于“修正量刑情节”，到底是采取“部分连乘、部分相加减”的调节程式，还是采取“同向相加、逆向相减”的调节程式。若是前者，则是复合模式；若是后者，则是单一模式。

例如，某案件中，被告人是未成年人减少基准刑50%的刑罚，且是从犯减少基准刑30%的刑罚，又具有累犯情节增加基准刑10%的刑罚，还具有自首情节减少基准刑20%的刑罚。如果采取复合模式进行计算，则被告人刑罚为：基准刑×（1-50%）×（1-30%）×（1+10%-20%）。如果采取单一模式进行计算，则被告人刑罚为：基准刑×（1-50%-30%+10%-20%）。

2.复合模式的优势和弊端

对于复合模式，最高人民法院戴长林法官进行了如下说明：从理论上讲，对“修正量刑情节”采用“同向相加、逆向相减”的单一模式得出的结果会出现零或者负数的情况。从适用情节合理性方面讲，不同类型的量刑情节进行简单加减，过于绝对化。从量刑思维过程来讲，对未成年、未遂等“修正量刑情节”，应当先对基准刑进行调节，再用其他情节进行调节，这样更符合刑法理论和量刑思维过程，得出的结果更具合理性。〔3〕参见戴长林、陈学勇：《量刑规范化改革与实践》，载《法律适用》2011年第9期。然而，上述文字只是给出了复合模式优于单一模式的结论，这些结论并不完全正确或者明晰。首先，就第一点来说，复合模式和单一模式都会出现零或者负数的情况，这并不是复合模式的优势；其次，就第三点来说，复合模式在哪些具体方面更具有合理性并不是很清晰。所以，需要更深入地比较两种调节程式的优劣。

徐嘎学者赞成复合模式，认为复合模式符合“罪行轻重不同的被告人如果具有相同的量刑情节，从轻的幅度相同但从轻的刑期可以不同”的量刑规律。例如，（案例1）甲盗窃他人活期存折一个，存折上存有30 万元，因甲取款时神色慌张，被银行人员发现而未能取走现金，属犯罪未遂，事后主动投案自首。（案例2）乙盗窃他人现金30 万元既遂，犯罪后主动投案自首。如果盗窃30 万元的基准刑为有期徒刑10 年，自首从轻20%，未遂从轻30%，那么按照复合模式，先考虑犯罪未遂情节，然后考虑自首情节，则案例1中甲盗窃30万元未遂中，自首从轻刑期是10×（1-30%）×20%，即1.4年；而案例2中甲盗窃30 万元既遂中，自首从轻刑期是10×20%，即2 年。两者从轻的幅度相同，但是从轻的刑期不同。案例1的未遂犯罪中，自首从轻的刑期要少些。这充分体现了“罪行轻重不同的被告人如果具有相同的量刑情节，从轻的幅度相同但从轻的刑期可以不同”的量刑规律。〔4〕参见徐嘎：《犯罪行为与犯罪人：量刑根据的二元化——兼论量刑规范化改革关于量刑步骤的合理构建》，载《山东审判》2010年第3期。案例根据本文需要，在细节上有所更改，但基本原理与原文一致。

耿磊学者则不赞成复合模式，认为单纯从数学角度出发，复合模式也存在以下问题。第一，“部分连乘、部分相加减”的调节程式将修正量刑情节与一般量刑情节相互关联、相互作用、相互影响，并且隔断了一般量刑情节对基准刑的直接作用。第二，认为运用复合模式的调节程式仍无法回避最终宣告刑为零和负数的尴尬。第三，立法原意本为强调修正量刑情节的影响，但是这种调节程式反而会降低修正量刑情节的影响。例如，（案例3）丙是未遂减少30%的刑罚，且具有自首也减少20%的刑罚。（案例4）丁是既遂，具有自首情节减少20%的刑罚，以及获得被害人谅解情节减少30%的刑罚。按照强调“修正量刑情节”的立法原意，整体上看，案例3采取复合模式减少的刑期应该比案例4采取单一模式减少的刑期要多些；单个情节上看，未遂减轻的刑期应该比被害人谅解减轻的刑期要多些。然而，事实并非如此。在基准刑10年的情况下，整体上看，案例3中丙的量刑为：10×（1-30%）×（1-20%），为5.6年，减少4.4年；案例4中丁的量刑为：10×（1-20%-30%），为5年，减少5年。案例3减少的刑期比案例4减少的刑期要少些，这与立法原意相违背。并且，从单个情节上看，案例3中未遂减少2.4年，自首减少2年；〔5〕就案例3而言，按照《量刑指导意见》，应该是未遂减少3年，自首减少1.4年，与案例1相同。所以，这里耿磊学者的分析有误，但其最终结论却是正确的。案例4中被害人谅解减少3年，自首减少2年。未遂减轻的刑期少于被害人谅解减轻的刑期，也与立法原意相违背。〔6〕参见耿磊：《酌定量刑情节规范化路径》，法律出版社2017年版，第132-135页。案例根据本文需要，在细节上有所更改，但基本原理与原文一致。

上述两位学者列举类似的案例，却得出截然不同的结论。就一般量刑情节的量刑效果而言，徐嘎学者的观点是正确的。在相同的基准刑和调节幅度下，相比于单一模式，复合模式减轻的刑期要少些。根本原因在于，复合模式中，修正量刑情节的连乘法使得基准刑处于不停减少的状况。基准刑的减少使得调节幅度相同的一般量刑情节，实际减少或者增加的刑期也要少些。

然而，耿磊学者的最终结论也是正确的。复合模式中的连乘法，并没有如立法原意所示，强化“修正量刑情节”的减轻幅度，反而弱化了“修正量刑情节”的减轻幅度。首先，案例3中未遂情节减轻的30%，等于案例4中被害人谅解情节减轻30%，均为3年。“修正量刑情节”未遂情节减轻的刑期并不比“一般量刑情节”被害人谅解减轻的刑期多，没有如立法原意强化“修正量刑情节”的减轻幅度。其次，如果同时存在两个及以上的“修正量刑情节”的情况下，可以认为第二个以后的“修正量刑情节”减轻的刑期要比“一般量刑情节”减轻的刑期少。例如，（案例5）戊是未成年减少50%的刑罚，同时是未遂减少30%的刑罚，还具有自首也减少20%的刑罚。在基准刑为10年的情况下，案例5中未遂减少的30%是以5年为基准刑，减少1.5年的刑期。而案例4中，被害人谅解减轻的30%是以10年为基准刑，减少的是3年的刑期，远远多于案例5“修正量刑情节”未遂减轻的刑期。最后，不仅就单个情节而言，“修正量刑情节”未遂减轻的刑期不多于“一般量刑情节”被害人谅解减轻的刑期。并且，整体而言，有“修正量刑情节”的案例中减轻的刑期要小于没有“修正量刑情节”的案例。例如，有“修正量刑情节”的案例3中，减轻的刑期为4.4年，小于没有“修正量刑情节”的案例4中减轻的刑期5年。这也说明复合模式的连乘法，没有强化“修正量刑情节”的减轻幅度。

由此可见，复合模式较单一模式更为复杂，但在理论上并不具有明显的优势，相反，其弊端很明显。首先，复合模式的基准刑处于不停的变动中，使得基准刑失去了作为“基准”的意义。其次，复合模式中的连乘法，并没有如立法原意所示，强化“修正量刑情节”的减轻幅度。

所以，要支持复合模式，必须从司法实务角度出发。如果复合模式得到的宣告刑值，比单一模式得到的宣告刑值，更接近司法实践中的实际宣告刑值，那么尽管复合模式理论上有诸多不足，也值得提倡。反之，如果复合模式得到的宣告刑值，并不比单一模式得到的宣告刑值，更接近司法实践中的实际宣告刑值，则复合模式不值得提倡。本文将利用盗窃罪案例的数据，通过实证研究方法，来考察复合模式的预测宣告刑，是否要比单一模式的预测宣告刑更接近司法的实际宣告刑。

值得说明的是，我国司法实践中的量刑方法来源于复合模式，是否司法实践得到的宣告刑就一定会更符合复合模式呢？其实不然。首先，我国幅员辽阔，各地即使是严格按照复合模式去执行，仍然在选择量刑起点、调节比例时存在自由裁量权，这种自由裁量权导致各地的执行结果并不一定一致地符合同一个复合模式。例如，甲地盗窃罪量刑起点为2 000元，未遂的调节比例为30%，自首的调节比例为30%；而乙地盗窃罪量刑起点选择3 000元，未遂的调节比例为50%，自首的调节比例为20%。假设，行为人A盗窃6 000元财物，那么，甲地对A在量刑起点4个月的基础上，增加4个月，构成基准刑8个月，然后因为未遂减少30%，得到5.6个月，最后因为自首减少30%，得到宣告刑3.92个月。不同的是，乙地对A在量刑起点6个月基础上，增加3个月，构成基准刑9个月，然后因为未遂减少50%，得到4.5个月，最后因为自首减少20%，得到宣告刑3.6个月。对甲地和乙地两种不同情况进行一般线性回归的结果，可能是复合模式：8×（1-40%）×（1-20%），拟合的宣告刑为3.84个月，也可能是单一模式：8×（1-38%-15%），拟合的宣告刑为3.76个月。复合模式中，预测值和实际宣告刑的残差平方和为0.064；单一模式中，预测值和实际宣告刑的残差平方和为0.051；前者大于后者，所以单一模式要优于复合模式。〔7〕从统计学角度看，残差平方和小的拟合方程更具有优势。可见，对于具有裁量差异的来源于复合模式的实证数据，最后拟合的复合模式和单一模式之间的结果相差无几，并不一定得到复合模式优先于单一模式的结论。其次，复合模式和单一模式虽然形式上相差甚大，但是最后的实际量刑数值相差并不一定很大。例如，在基准刑是10年的基础上，未遂减少50%，自首减少20%的情况下，复合模式为：120×（1-50%）×（1-20%），宣告刑为48个月；而单一模式为：120×（1-50%-20%），宣告刑为36个月。两者相差12个月，即1年。这是相差较大的情况。基准刑越低的时候，两种模式的宣告刑相差越小。而司法实践中，绝大多数案件基准刑都小于5年，所以宣告刑也会相差较小。总之，司法实践中数据虽然来源于复合模式，但是众多案例汇总后线性回归拟合的结果并非一定是复合模式优先于单一模式。

如果众多案例汇总后得到的结果是单一模式优先于复合模式，那么即使实际数据来源于复合模式，我们仍应该将之统一为单一模式，从而实现基准刑调节程式的简化改革。这样简化改革的结果当然会造成各地裁量权的减弱，但是会使各地量刑更加具体化和统一化。

（二）两种调节幅度模式的争议

1.《量刑指导意见》中的调节幅度模式：比例固定

我国《量刑指导意见》中的调节幅度模式是“比例固定”模式。所谓的“比例固定”模式是指，常见量刑情节对基准刑的调节比例虽然存在一定的浮动幅度，但是这一浮动幅度是针对情节本身的严重程度而言的，并不是针对不同罪名而言；对于不同的罪名，同一常见量刑情节的调节比例相对固定。例如，《量刑指导意见》第3条第1项规定，已满16周岁不满18周岁的未成年人犯罪，减少基准刑的10%～50%。那么，针对不同的罪名，未成年犯罪均减少基准刑的刑罚幅度范围一致，均为10%～50%。只是在不同案件中，具体减少的调节比例，根据犯罪行为的动机和目的、犯罪时的年龄和对犯罪的认识能力、悔罪表现、个人成长经历和一贯表现等来决定。〔8〕同前注〔2〕，南英主编书，第52页。

例如，（案例6）被告人己17岁11个月，辍学，经常小偷小摸，一次诈骗30万元，基准刑为8年。（案例7）被告人庚16岁5个月，学校表现良好，偶尔的一次盗窃30万元，基准刑为10年。在盗窃罪和诈骗罪两种不同的犯罪中，未成年情节调节基准刑的“比例固定”均为10%～50%。但是案例6中，被告人是一贯表现不好，且年龄稍长；而案例7中被告人一贯表现好，且年龄稍小。所以，案例6中未成年减轻比例可以设定为20%，而案例7中未成年减轻比例可以设定为40%。

2.“集体经验法”中的调节幅度模式：数值固定

对于调节幅度模式，除了《量刑指导意见》中的“比例固定”模式外，还有白建军教授主张的“集体经验说”中的“数值固定”模式。

“集体经验说”是一种根据法官集体经验，利用统计学方法构建起来的量刑模式。〔9〕该量刑方法即统计学中的回归方法，参见白建军：《基于法官集体经验的量刑预测研究》，载《法学研究》2016年第6期。“集体经验说”具有以下几个特点：第一，“集体经验说”计算刑罚的公式是一个线性回归方程。用数学公式表达为：刑罚量=b0+b1×基准事实情节1+b2×基准事实情节2+b3×一般量刑情节1+b4×一般量刑情节2+……+bn×一般量刑情节n。第二，量刑起点为“裸刑均值”，处于法定刑的偏低幅度。“裸刑均值”是指一组没有其他量刑情节，只有犯罪构成事实的生效判决的刑罚均值。〔10〕参见白建军：《裸刑均值的意义》，载《法学研究》2010年第6期。第三，基准事实是对刑罚量影响最大的几个量刑情节。例如，在醉酒型危险驾驶罪中，对刑罚量影响最大的量刑情节是血液酒精含量、车型等，所以其基准刑可通过血液酒精含量、车型来构建。〔11〕参见文姬：《醉酒型危险驾驶罪量刑影响因素实证研究》，载《法学研究》2016年第1期。第四，基准刑是在量刑起点的基础上通过加法的方式获得。以刑罚量（或者刑罚的对数变形〔12〕例如，有时候为了满足线性回归的方差齐性的要求，将因变量或者自变量进行Lg或者Ln的对数变形。）为自变量，以量刑情节（或者量刑情节数值的对数变形）为因变量的回归，一般来说是线性回归。所以，基准刑与基准事实取值之间要么是呈线性增长，要么是呈指数增长或者对数增长。指数增长和对数增长也可以转化为分段的线性增长。例如，就醉酒型危险驾驶罪来说，对所有的样本案件进行线性回归，得到回归直线，从而得到基准刑的程式：拘役天数=28.581+0.241×血液酒精含量。〔13〕同前注〔11〕，文姬文。所以，其量刑起点为：拘役天数=28.581+0.241×80，约为48天。刑罚增量为：血液酒精含量每增加6mg/100mL，刑期增加1个月。第五，调节程式为“同向相加，逆向相减”的单一模式。因为“集体经验法”是运用的线性回归方法，量刑情节之间是以加减法相连接的。第六，调节幅度模式为“数值固定”模式，即常见量刑情节对基准刑的调节幅度模式是通过加减固定的数值，而非加减固定的比例。

“集体经验说”中，调节幅度模式为“数值固定”模式。例如，自首在盗窃数额为5万元～40万元的盗窃罪中，回归系数为12.544。其代表的意义是，具有自首情节的案件比具有配合情节的案件，行为人的刑期要少约13个月。〔14〕数据见本文第二部分表1中盗窃数额为5万元～40万元时的“数值固定”模式。也就是说，在盗窃罪中，自首情节是在基准刑的基础上增加“固定数值”的刑期，即13个月。

比较而言，《量刑指导意见》中的调节幅度模式为“比例固定”模式。例如，《量刑指导意见》规定自首减少基准刑的40%以下的刑罚量。假设减少40%，那么用数学公式表示自首减轻的刑期为：40%×基准刑=40%×（量刑起点+刑罚增量）。按照江苏省的规定来算，5万元～40万元的盗窃罪中，盗窃5万元对应的量刑起点为42个月，每增加5 000元增加1个月的基准刑。自首则减少的刑期为：40%×（量刑起点+刑罚增量）=40%×（42+盗窃数额增量），约17个月到45个月不等。可见，同一个罪名中，因为基准刑随着盗窃数额的增加而不同，自首减少的天数也不同。不同的罪名中，由于量刑起点和刑罚增量的不同，自首减少的天数也不相同。自首减少的天数，与量刑起点数成正比，与刑罚增量成正比。所以，在《量刑指导意见》中，自首对基准刑的调节幅度不是“数值固定”，而是“比例固定”。

3.“比例固定”模式与“数值固定”模式的区别

《量刑指导意见》中的“比例固定”模式和“集体经验说”中的“数值固定”模式均来源于法官的集体经验，这使得它们在本质上具有相同性。〔15〕《量刑指导意见》中常见情节的调节比例的确定方法，并不能从公开的资料获得。《量刑指导意见》的开头指出：“根据刑法和刑事司法解释等有关规定，结合审判实践，制定本指导意见。”可见，《量刑指导意见》中常见情节的调节比例的确定，肯定参考了审判中的大量案例。所以，称其为“来源于法官的集体经验”。但是，“比例固定”模式和“数值固定”模式还是存在以下两点显著差别。

首先，“比例固定”模式较“数值固定”模式更为复杂。其一，“数值固定”模式中，量刑情节对基准刑的调节数值是固定不变的。而在“比例固定”模式中，调节数值实际上与量刑起点和刑罚增量均成正比。在同一罪名的不同量刑幅度或者不同罪名中，量刑起点和刑罚增量处于不断变动中，从而“比例固定”模式中的调节数值也随着两者的变动而处于不断的变动中。其二，如果将“比例固定”模式的公式拆分成由加减法构成的线性模式，〔16〕参见本文第二部分：调节幅度模式的实证研究中的关于两种调节幅度模式的“理论模型”。会发现在没有“修正情节”的情况下，“比例固定”模式比“数值固定”模式多了“盗窃数额”与所有量刑情节的交互项，也就是说，“比例固定”模式考虑了交互影响，而“数值固定”模式没有考虑交互影响。

其次，“比例固定”模式中，同一常见量刑情节在不同罪名中的调节比例是“固定”的；而在“数值固定”模式中，同一常见量刑情节在不同罪名中的调节数值是不固定的。《量刑指导意见》中给出未成年、未遂、从犯、自首、坦白、立功等情节的调节幅度，分别为10%～60%、0%～50%、20%～100%、0%～100%、0%～50%、0%～100%，并且，影响具体调节幅度的因素包括具体年龄、犯罪的严重程度、情节的社会效果等，但是，罪名并没有成为具体调节幅度的影响因素。

罪名是否对同一情节的调节幅度具有显著影响，这一问题的论证是个复杂的系统工程，笔者将另行赘述。对于量刑情节对基准刑的调节数值，是否应当与“基准刑”成正比，是否应当考虑“盗窃数额”与其他情节的交互效应，这两个问题都是纯数据方面的问题，理论上没有优劣可言。所以，本文通过实证研究对两者进行比较。并且，“比例固定”模式和“数值固定”模式两者本质上均是“法官集体经验”的产物，其构建的主要依据都是“一定数量的判决书”，所以应当从经验上去论证两者的优劣：与实践拟合度更高的调节幅度模式更具有优势。如果两种调节幅度模式没有显著差异，则应当选择更为简单易行的“数值固定”模式。

二、调节幅度模式的实证研究

根据公安部门的统计资料，2013年到2015年间，盗窃罪立案数占到公安部门总立案数的67%～68%。〔17〕数据来源于《中国法律年鉴》2014、2015、2016年版本中的第1141、1022、1305页。本文盗窃罪判决书的判决日期为2013—2015年。所以本文以盗窃罪为例，根据盗窃罪的实证数据，比较在调节程式为“同向相加、逆向相减”的情况下，“比例固定”和“数值固定”两种不同调节幅度模式的优劣。

两种不同调节幅度模式的优劣比较步骤如下：首先，利用司法实践数据估算出“比例固定”模式和“数值固定”模式的理论模型的系数；其次，根据两种理论模型，计算出各自的预测宣告刑；再次，计算两个预测宣告刑与实际宣告刑之间的差的平方和，也就是残差平方和；最后，检验两种残差平方是否具有显著性差异。残差平方和显著偏小的调节幅度模式更具有优势。

本文的数据来源于“中国裁判文书网”，收集日期为 2016年7月26日。在136 570个盗窃罪中，按照分层随机方法，抽取了 1 806份判决书，〔18〕首先，按照各省人口比例对2 000份判决书进行分配，然后，对各省的判决书按照随机等距抽样方法进行随机抽样。删除其中一些数据不完整、重复的案例，剩下1 806份案例。形成 2 355个记录。〔19〕因为存在共同犯罪，所以记录数多于判决书数目。

（一）案例选择

合适的案例是计算出理论模型系数的基础。

首先，案例中必须排除连乘法的适用。在“同向相加、逆向相减”的调节程式中，不能出现连乘法。所以本文选择没有“未成年犯罪、老年犯罪、限制行为能力的精神病人犯罪、又聋又哑的人或者盲人犯罪、防卫过当、避险过当、犯罪预备、犯罪未遂、犯罪中止、从犯、胁从犯、教唆犯”等“修正量刑情节”的案例记录共2 113个。

其次，为了比较研究更容易实行，本文只考虑以“盗窃数额”为基准事实的情况。所以，理想状况下，本文还要选择没有“扒窃、多次盗窃、入户盗窃、携带凶器盗窃”情节的案例，从而排除以盗窃次数、盗窃手段为基准事实的情况出现。但是，在删除所有的“扒窃、多次盗窃、入户盗窃、携带凶器盗窃”案例的情况下，5万元～40万元的记录只有66个，40万元及以上的记录只有16个，导致样本量不够。所以，本文仅仅在0～5万元阶段删除所有有“扒窃、多次盗窃、入户盗窃、携带凶器盗窃”情节的案例，而在5万元～40万以及40万元以上的情况下，不删除有“扒窃、多次盗窃、入户盗窃、携带凶器盗窃”情节的案例。另外，因为单处罚金和管制并没有统一折算的方法，加之记录数量较少，所以予以删除。还有，根据散点图，盗窃数额0～5万元的记录中有1个异常值，最终得到盗窃数额为0～5万元的记录770个，5万元～40万元的记录198个，40万元及以上的记录40个，共1 008个记录。

（二）两种调节幅度模式的理论模型

在1 008个盗窃罪记录中，除盗窃数额外，量刑情节包括初犯、被害人谅解、积极缴纳罚金和财产保证、立功、退赃退赔、认罪态度（包括自首、坦白、配合）、前科、累犯、其他从轻情节、其他从重情节、携带工具等。

1.“比例固定”模式的理论模型

在“同向相加、逆向相减”的调节程式下，“比例固定”模式的盗窃罪的刑罚量计算公式为：盗窃罪拘役刑或徒刑刑期=（b0+b1×盗窃数额）×（1+a1×初犯+a2×被害人谅解+a3×积极缴纳罚金和财产保证+a4×立功+……+a12×携带工具+a13×扒窃+a14×多次盗窃+a15×入户盗窃+a16×携带凶器盗窃）=b0+b1×盗窃数额+c1×初犯+c2×被害人谅解+c3×积极缴纳罚金和财产保证+c4×立功+……+c12×携带工具+c13×扒窃+c14×多次盗窃+c15×入户盗窃+c16×携带凶器盗窃+d1×初犯×盗窃数额+d2×被害人谅解×盗窃数额+d3×积极缴纳罚金和财产保证×盗窃数额+d4×立功×盗窃数额+……+d12×携带工具×盗窃数额+d13×扒窃×盗窃数额+d14×多次盗窃×盗窃数额+d15×入户盗窃×盗窃数额+d16×携带凶器盗窃×盗窃数额。其中，（b0+b1×盗窃数额起点）是量刑起点，（b1×盗窃数额增量）为基准刑的刑罚增量，（b0+b1×盗窃数额）是基准刑。（c1+d1×盗窃数额）/（b0+b1×盗窃数额）是初犯情节的调节比例……（c16+d16×盗窃数额）/（b0+b1×盗窃数额）是携带凶器盗窃情节的调节比例。〔20〕公式中比量刑情节数多一项，是因为认罪情节在公式中拆分为了两项：自首、坦白。配合是参照情节，不体现在公式中。

之所以将理论模型拆解为一般线性方程，是因为我们在求解最优回归方程时，是用“一般线性回归”方法求得。所以，将理论模型拆解为一般线性方程，以便进行对比研究。

2.“数值固定”模式的理论模型

“数值固定”模式，也即“集体经验法”中的调节幅度模式。其刑罚的计算公式为：盗窃罪拘役刑或徒刑刑期=B0+B1×盗窃数额+C1×初犯+C2×被害人谅解+C3×积极缴纳罚金和财产保证+C4×立功+……+C16×携带凶器盗窃。其中，（B0+B1×盗窃数额起点）是量刑起点，（B1×盗窃数额增量）为基准刑的刑罚增量，（B0+B1×盗窃数额）是基准刑。C1是初犯情节的调节数值……C16是携带凶器盗窃情节的调节数值。

3.理论模型系数的计算

理想状况下，上述两种理论模型的系数均能够运用盗窃罪的司法数据通过“一般线性回归”方法求得。并且，在“比例固定”模式的理论模型中，各种量刑情节的比例能够被计算出来，即（c1+d1×盗窃数额）/（b0+b1×盗窃数额）……（c16+d16×盗窃数额）/（b0+b1×盗窃数额）能够除尽，没有余数。

然而，理想情况几乎不可能出现。一般会出现以下两种不理想的状况：第一，某些量刑情节不能够被纳入方程。例如，利用本文数据，在两种理论模型的拟合中，初犯情节的交互效应项〔21〕交互效应项，是指线性方程中有两个及以上量刑情节共同构成的项。如d1×初犯×盗窃数额、d2×被害人谅解×盗窃数额、d3×积极缴纳罚金和财产保证×盗窃数额、d4×立功×盗窃数额、……、d16×携带凶器盗窃×盗窃数额。和主效应项〔22〕主效应项，是指线性方程中只有一个量刑情节构成的项。如c1×初犯、c2×被害人谅解、c3×积极缴纳罚金和财产保证、c4×立功、……、c16×携带凶器盗窃等。的系数均大于零。这说明无论如何，初犯情节对刑罚的影响均为正向关系，即初犯情节导致刑罚量增加，这显然与初犯情节是从轻情节的理论相矛盾。所以，初犯情节不能被纳入方程中。第二，“比例固定”模式的模型中，各个量刑情节的比例不能够被除尽，即（c1+d1×盗窃数额）/（b0+b1×盗窃数额）……（c12+d12×盗窃数额）/（b0+b1×盗窃数额）中全部或者部分不能够被除尽，这说明纯粹的“比例固定”模式的理论模型在某种程度上不能够被获得。

基于以上两种不理想的状况，本文采取变通的方法计算理论模型的系数，分别求出具有交互效应项的最优回归方程和不具有交互效应项的最优回归方程，用前者来拟合“比例固定”模式的理论模型，用后者来拟合“数值固定”模式的理论模型。因为从上面两种理论模型的一般线性展开项可以发现，“比例固定”模式与“数值固定”模式的理论模型的主要区别在于，“比例固定”模式中具有交互效应项，而“数值固定”模式中不具有交互效应项，所以用具有交互效应项的最优回归方程拟合“比例固定”模式的理论模型，而用没有交互效应项的最优回归方程拟合“数值固定”模式的理论模型。

（三）最优调节幅度模式的获取方法

计算出理论模型的系数后，还需要比较两个最优回归方程中，哪个方程更具有实践优势。这需要用“均值比较”方法进行检验。

首先，利用“一般线性回归”方法得到“比例固定”和“数值固定”两种模式各自的最优回归方程的同时，也可以计算出两者的预测宣告刑。其次，计算预测宣告刑与实际宣告刑的差的平方和，即残差平方和。残差平方和小的调节幅度模式效果更佳。这是典型的“最小二乘法”思想。〔23〕参见理查德·P.鲁尼恩、凯·A.科尔曼、戴维·J.皮滕杰：《行为统计学基础》（第9版），王星译，中国人民大学出版社2007年版，第183页。最后，还需要用“成对样本均值检验法”检验两个残差平方是否具有显著性差异。因为即使两种调节幅度模式的预测宣告刑与实际宣告刑具有一定的差异（其实具有差异是肯定的），还需要知道这种差异是否具有显著性。如果具有显著性，则说明两种模式中，残差平方和小的调节幅度模式确实具有显著优势；如果不具有显著性，则说明残差平方和小的调节幅度模式并不具有显著优势。具有显著优势的调节幅度模式，才是我们要提倡的最优调节幅度模式。所以，还需要检验两个预测宣告刑与实际宣告刑的差的平方之间均值是否具有显著性差异。这种检验方法称为“成对样本均值检验法”。

（四）一般线性回归方程的结果分析

上述回归系数和预测宣告值的求得方法为统计软件SPSS中的一般线性回归方法。因为本文的最终目的是比较预测宣告刑和实际宣告刑之间的差的平方和，而非考察影响量刑的显著性因素，所以本文在进行一般线性回归时，将所有的量刑情节都纳入方程，而不考虑量刑情节的影响是否显著。

1.“比例固定”模式和“数值固定”模式的最优回归方程的获取

（1）“比例固定”模式的理想的理论模型不能够被获取

按照“比例固定”模式的理想的理论模型，应当将所有的量刑情节及其交互效应项均纳入方程。然而，本文的数据却显示，在盗窃数额为0～5万元回归方程中，并非所有的交互项均能够被纳入方程。

利用一般线性回归方法，在将所有的交互效应项均纳入模型后，得到自首的从轻的数值为-（0.000374×盗窃数额-0.452）。这一数值是基准刑（0.000768×盗窃数额+3.259）的-0.486倍又另外加上2.036个月（我们用-48.6%（+2.036）表示自首的调节比例）。〔24〕此处即为回归方程中，量刑情节调节基准刑的调节比例的计算方法。下面所有量刑情节的调节比例均用这种方式表示：百分数部分是调节比例，括号内的常数部分是另外加上的调节数值。并且，用同样的方法可以算得：初犯的调节比例为+59%（-5.602），被害人谅解的调节比例为-3.4%（-0.717），积极缴纳罚金或财产保证的调节比例为-7.2%（-1.436），立功的调节比例为+15.4%（-2.796），退赔退赃的调节比例为 +13.5%（-0.69），坦白的调节比例为-27.9%（+1.591），累犯的调节比例为 +8.2%（+2.012）；前科的调节比例为-9.6%（+1.618）；其他从轻情节的调节比例为+39.1%（-2.099），其他从重情节的调节比例为 +64.5%（-2.994），携带工具的调节比例为-8.7%（+0.863）。〔25〕将所有交互效应项均纳入方程后，得到的线性回归方程为：3.259+0.000768×盗窃数额-3.679×初犯-0.828×被害人谅解-1.671×积极缴纳罚金和财产保证-2.294×立功-0.257×退赔退赃+0.452×自首+0.682×坦白+1.305×前科+2.279×累犯+0.825×其他从轻情节-0.892×其他从重情节+0.580×携带工具+0.000453×初犯×盗窃数额-0.000026×被害人谅解×盗窃数额-0.000055×积极缴纳罚金和财产保证×盗窃数额+0.000118×立功×盗窃数额-0.000104×退赔退赃×盗窃数额-0.000347×自首×盗窃数额-0.000214×坦白×盗窃数额-0.000074×前科×盗窃数额+0.000063×累犯×盗窃数额-0.00030×其他从轻情节×盗窃数额+0.000495×其他从重情节×盗窃数额-0.000067×携带工具×盗窃数额。

可以看到，将所有的交互效应项均纳入方程后，会出现与理论矛盾的情况。例如，前科、携带工具的调节比例为负数，说明在该模型中该情节减轻刑期；可是前科、携带工具本是从重情节，却从轻处罚，不符合理论设定。又如，立功、退赔退赃、其他从轻情节的调节比例为正数，说明在该模型中该情节增加刑期；可是立功、退赔退赃、其他从轻情节本是从轻情节，却从重处罚，也不符合理论设定。所以并非所有的交互效应项都能够被纳入方程，即“比例固定”模式的理想的理论模型不能够被获取。

（2）两种调节幅度模式的最优回归方程的拟合

经过调整，在符合理论的从轻从重处罚原则的基础上，模型中含有交互效应项的数目不同，模型调整R方也不相同。我们是取交互效应项数目最多的模型，还是取模型调整R方最大的模型呢？

从表面上看，我们的目的是比较“比例固定”与“数值固定”模型的优劣，而“比例固定”模式与“数值固定”模式的不同就在于有交互效应项，所以应当取交互效应项数目最多的模型，而非调整R方最大的模型。然而，我们比较“比例固定”与“数值固定”两种模式优劣的目的，却是为了找到可以更好地与司法实务数据相契合的调节幅度模式。也就是说，找到某种调节幅度模式，其预测宣告刑与实际宣告刑之间的“差的平方和”最小。而调整R方最大的模式，其预测宣告刑与实际宣告刑之间的“差的平方和”才是最小的。所以，在“比例固定”模式中，我们应当选取具有交互效应项的调整R方最大的模型，即“比例固定”模式的最优回归方程；在“数值固定”模式中，我们应当选取没有交互效应项的调整R方最大的模型，即“数值固定”模式的最优回归方程。

（3）“准比例固定”模式取代纯粹的“比例固定”模式

因为“比例固定”模式理想的理论模型不能够被获取，所以即使在引入交互效应项的最优回归方程中，交互效应项的数目也不多。其中没有交互效应项的量刑情节，仍然需要采取“数值固定”的调节幅度方法，从而导致有交互效应项的最优回归方式，实际上是“部分比例固定、部分数值固定”的线性回归方程。也就是说，现有的《量刑指导意见》中的“比例固定”模式在司法实践中只能是“部分比例固定、部分数值固定”的调节幅度模式（简称为“准比例固定”模式）。

在比较两个最优回归方程后，若结论是“交互效应项有必要被引入”，则说明“准比例固定”模式更优越；若结论是“交互效应没有必要被引入”，则说明“数值固定”模式更优越。

2.“准比例固定”模式和“数值固定”模式的比较

（1）两种模式最优回归方程的获取

运用SPSS中一般线性回归方法，利用盗窃数额为0～5万元的770个记录，盗窃数额为5万元～40万元的198个记录，以及盗窃数额为40万元及以上的40个记录，得到表1的模型拟合系数。

（2）盗窃数额为0～5万元的调节幅度模式比较

从表1可以看出，“准比例固定”模式中，“比例固定”的情节包括：被害人谅解、积极缴纳罚金或财产凭证、退赔退赃、认罪态度、其他从重情节等；“数值固定”的情节包括：累犯、前科等。

从表1中还可以看出，“准比例固定”模式中，预测宣告刑与实际宣告刑差的平方和4 903.39，要小于“数值固定”模式中差的平方和5 684.18。并且残差平方的均值检验中，其显著性检验的sig值为0.036，小于0.05，具有显著性。〔26〕显著性检验的sig值小于0.05即具有显著优势。也即是说，“准比例固定”模式要优于纯粹的“数值固定”模式。

（3）盗窃数额为5万元～40万元的调节幅度模式比较

用同样的方法，得到表1中盗窃数额为5万～40万元的模型系数及残差平方的均值检验结果。从表1中可以看出，“数值固定”模式中，预测宣告刑与实际宣告刑的差的平方和41 478.60，大于“准比例固定”模式中预测宣告刑与实际宣告刑的差的平方和21 855.07；并且，在残差平方的均值检验中，其显著性检验的sig值为0.006，小于0.05，具有显著性。“准比例固定”模式比“数值固定”模式，从统计学上看具有显著优势。所以，对于盗窃数额为5万元～40万元的模型来说，引入交互效应项是有必要的，应当采取 “准比例固定”模式。

（4）盗窃数额为40万元及以上的调节幅度模式比较

用同样的方法，得到表1中盗窃数额为40万元及以上的模型系数以及残差平方的均值检验结果。从表1中可以看出，“数值固定”模式中，预测宣告刑与实际宣告刑的差的平方和10 007.01，大于“准比例固定”模式中预测宣告刑与实际宣告刑的差的平方和9 533.29；但是，在残差平方的均值检验中，其显著性检验的sig值为0.405，大于0.05，不具有显著性。所以，“数值固定”模式与“准比例固定”模式之间没有显著差异，从统计学上看，两者具有相同的优势。所以，对于盗窃数额为40万元及以上的模型来说，采取 “数值固定”模式更简洁易行。

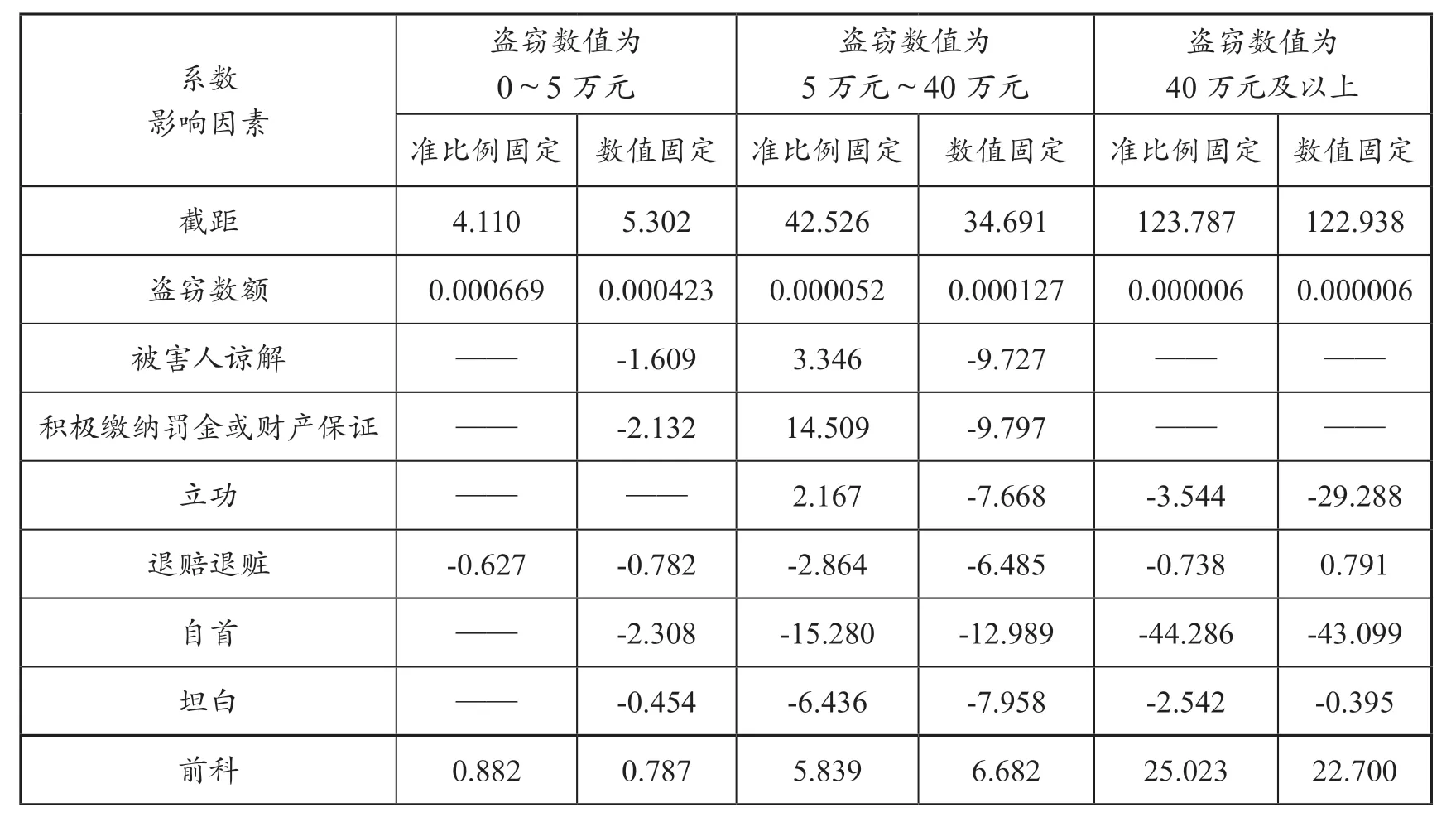
表1 准比例固定模式与数值固定模式的对比研究〔27〕对于一般线性回归后，所有方程中均没有纳入的量刑影响因素，表格中不再列出。下文的表格均与此相同。

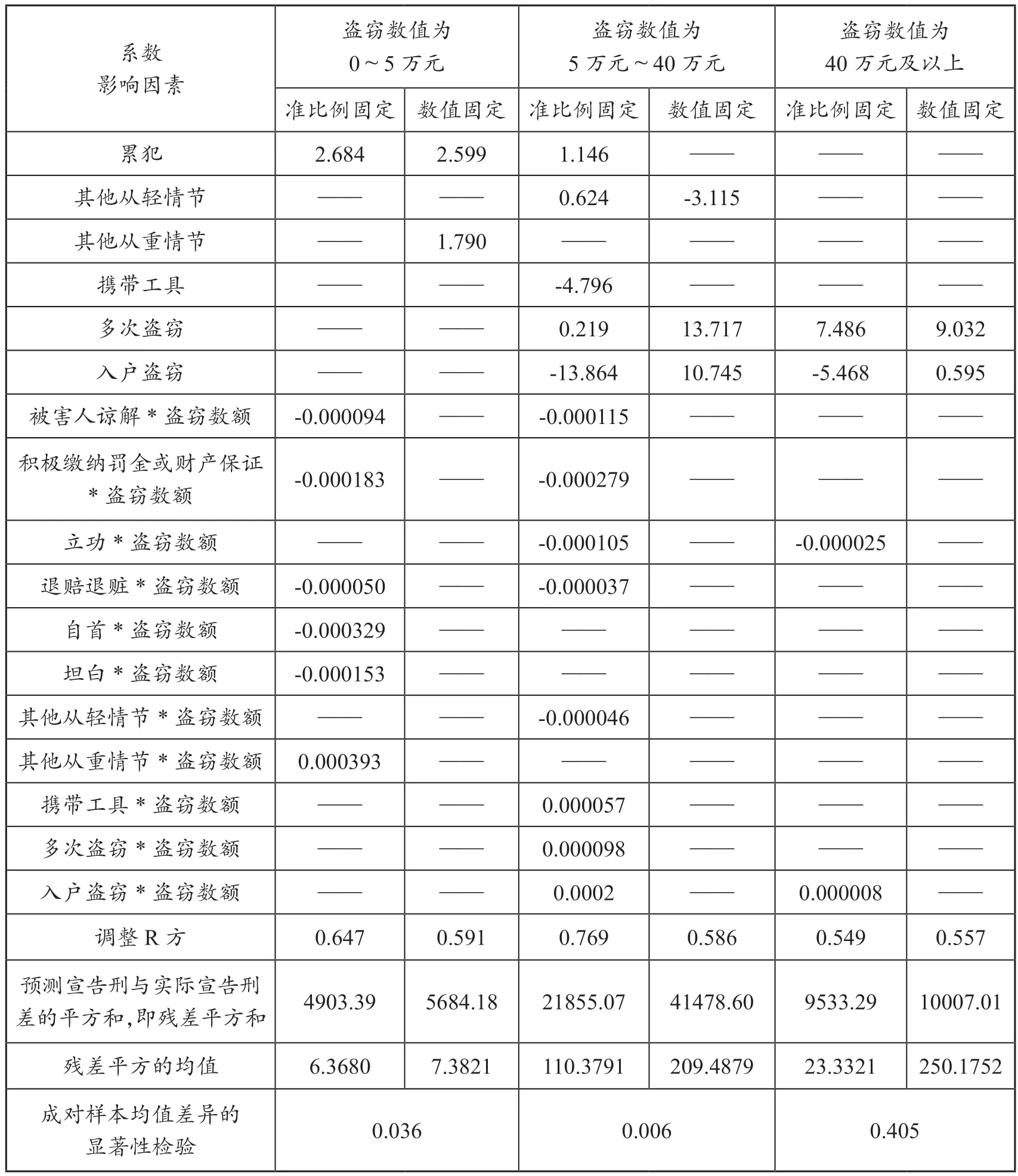
（续表）

3.具体调节比例和调节数值的计算

从表1中可以计算出盗窃数额为0～5万元的“准比例固定”模式中调节比例的具体数值。被害人谅解的调节比例为-14.1%（+0.580），积极缴纳罚金或财产凭证的调节比例为-27.4%（+1.126），退赔退赃的调节比例为-7.5%（-0.319），自首的调节比例为-49.2%（+2.022），坦白的调节比例为-22.9%（+0.941），其他从重情节的调节比例为58.7%（-2.413）。

对于“数值固定”的量刑情节来说，其调节幅度的固定数值，即为表1中该情节对应的回归方程的系数，不需要另外计算。例如，在“准比例固定”模式中，累犯的调节数值为直接在基础刑的基础上加上+2.684个月，前科的调节数值为+0.882个月。

从表1中还可以计算出盗窃数额为5万元～40万元的调节数值。被害人谅解的调节比例为-221.15%（+97.392），积极缴纳罚金或财产凭证的调节比例为-536.54%（+242.678），立功的调节比例为-201.92%（+88.035），退赔退赃的调节比例为-71.15%（+27.443），其他从轻情节的调节比例为-88.46%（-38.242），携带工具的调节比例为 109.62%（-51.413），多次盗窃的调节比例为 188.46%（-79.925），入户盗窃的调节比例为384.62%（-177.428）。另外，还有一些情节是“数值固定”调节模式：自首的调节数值为-15.280，坦白的调节数值为-6.436，前科的调节数值为+5.839，累犯的调节数值为+1.146。

当然，从表1中也可以计算出盗窃数额为40万元及以上的调节数值。即立功的调节数值为-29.288个月，退赔退赃的调节数值为-0.791个月，自首的调节数值为-43.099个月，坦白的调节数值为-0.395个月，前科的调节数值为+22.7个月，多次盗窃的调节数值为+9.032个月，入户盗窃的调节数值为+0.595个月。

4.调节幅度模式比较的结论

总结表1的数据可以得出，对于盗窃数额为0～5万元和5万元～40万元的最优回归方程来说，有必要引入交互效应项；而对于盗窃数额为40万元及以上的最优回归方程说，没有必要引入交互效应项。也就是说，对于盗窃数额为0～5万元和5万元～40万元的犯罪来说，“准比例固定”模式要优于纯粹“数值固定”模式；而对于盗窃数额为40万元及以上的犯罪来说，“数值固定”模式更为可取。

可见，不同的情况下，调节基准刑的模式不同。有的时候是比例固定，有的时候是数值固定，而非“一刀切”地“比例固定”或者“数值固定”。即使在盗窃数额为0～5万元和5万元～40万元的最优回归方程中，有的情节是“比例固定”模式，而有的情节是“数值固定”模式。

另外，一般来说，纯粹的“比例固定”调节方式并不可取，因为这种模式会导致量刑情节对基准刑的调节幅度不符合理论上从轻从重处罚原则的要求。

三、调节程式的实证研究

在得出调节幅度必须兼顾“准比例固定”和“数值固定”两种模式的基础上，利用上述2 355个盗窃罪记录来比较调节程式中复合模式与单一模式的优劣。

（一）案例选择

首先，选择包含“从犯”情节，但还不包含未成年及限制行为能力情节和从犯情节的案件。两种调节程式的比较必须包含“未成年犯罪、老年犯罪、限制行为能力的精神病人犯罪、又聋又哑的人或者盲人犯罪、防卫过当、避险过当、犯罪预备、犯罪未遂、犯罪中止、从犯、胁从犯、教唆犯”等情节中的一个或者多个。本文的数据中包含了未成年或限制行为能力人犯罪、犯罪未遂、从犯这三种情节。如果将三种情节同时纳入考虑将导致回归方程十分复杂，为了比较研究更容易，本文选择只包含“从犯”这一个情节的案例，共有2 209个记录。

其次，为了比较研究更容易实行，本文只考虑以“盗窃数额”为基准事实的情况下，量刑情节对基准刑的调节方法。理想状态下应当选择没有“扒窃、多次盗窃、入户盗窃、携带凶器盗窃”情节的案例。但是，若将包含上述情节案例全部删除，最后剩下的含有“从犯”情节的案例会很少，导致本文带有“连乘法”的复合模式无法实现。所以，我们选择了折中的方法，在盗窃数额为0～5万元及5万元～40万元时，删除含有多次盗窃、携带凶器盗窃的案例，而保留具有“扒窃、入室盗窃”量刑情节的案例；在盗窃数额为40万元及以上时，保留所有多次盗窃、携带凶器、扒窃、入室盗窃的案例。

最后，因变量的刑罚种类中，本文只选择有期徒刑和拘役两种。因为单处罚金和管制并没有统一折算的方法，加之记录数量较少，所以予以删除。剩下盗窃数额为0～5万元的记录1 204个，盗窃数额为5万元～40万元的记录102个，盗窃数额为40万元及以上的记录51个。

（二）两种调节程式的理论模型

上述1 357个记录中，除盗窃数额、从犯外，量刑情节还包括初犯、被害人谅解、积极缴纳罚金或财产保证、立功、退赃退赔、认罪态度、前科、累犯、其他从轻情节、其他从重情节、多次盗窃、携带工具、入室盗窃、扒窃等。值得注意的是，对于盗窃数额为5万元～40万元，以及40万元及以上的情况，本文删除了影响因素频次小于5的影响因素，不纳入一般线性回归。〔28〕因为如果原有影响因素的记录数就小于5个，那么当该影响因素与其他因素形成交互作用项时，该交互作用项的记录更少，甚至为0，这样导致一般线性回归系数异常，所以予以删除。

1.复合模式的理论模型

复合模式的刑罚量计算公式为：盗窃罪拘役刑或徒刑刑期=（b0+b1×盗窃数额）×（1+b2×从犯）×（1+a1×初犯+a2×被害人谅解+a3×积极缴纳罚金或财产保证+a4×立功+a5×退赃退赔+a6×认罪态度+a7×前科+a8×累犯+……+a15×扒窃）=b0+b1×盗窃数额+c0×从犯+c1×初犯+c2×被害人谅解+c3×积极缴纳罚金或财产保证+c4×立功+c5×退赔退赃+c6×认罪态度+c7×前科+……+c15×扒窃+d0×从犯×盗窃数额+d1×初犯×盗窃数额+d2×被害人谅解×盗窃数额+d3×积极缴纳罚金或财产保证×盗窃数额+d4×立功×盗窃数额+d5×退赃退赔×盗窃数额+d6×认罪态度×盗窃数额+d7×前科×盗窃数额+d8×累犯×盗窃数额+……+d15×扒窃×盗窃数额+e1×初犯×从犯+e2×被害人谅解×从犯+e3×积极缴纳罚金或财产保证×从犯+e4×立功×从犯+e5×退赃退赔×从犯+e6×认罪态度×从犯+e7×前科×从犯+e8×累犯×从犯+……+e15×扒窃×从犯+f1×初犯×从犯×盗窃数额+f2×被害人谅解×从犯×盗窃数额+f3×积极缴纳罚金或财产保证×从犯×盗窃数额+f4×立功×从犯×盗窃数额+f5×退赃退赔×从犯×盗窃数额+f6×认罪态度×从犯×盗窃数额+f7×前科×从犯×盗窃数额+f8×累犯×从犯×盗窃数额+……+f15×扒窃×从犯×盗窃数额。

可以看出，这一理论模型拆分为一般线性回归方程后，共有64个相加项，其中交互效应项最多包含三个量刑情节。这还是只有一个“修正量刑情节”的情况。如果有两个“修正量刑情节”，拆分后将有128个相加项，其复杂程度可想而知。

2.单一模式的理论模型

如第二部分所证明的那样，在单一模式的情况下，必须兼顾“准比例固定”模式和“数值固定”模式。因为，“准比例固定”模式和“数值固定”模式均可以用带有交互效应项回归方程来表示，只是“数值固定”模式的方程中交互效应项的系数为零，而“准比例固定”的方程中交互效应项的系数不全部为零。所以，对于单一模式的回归方程，我们仍然按照“准比例固定”模式的回归方程，只是在必要的时候将交互效应项的系数设置为零即可。

可见，单一模式的理论模型为：盗窃罪拘役刑或徒刑刑期=（B0+B1×盗窃数额）×（1+A0×从犯+A1×初犯+A2×被害人谅解+A3×积极缴纳罚金或财产保证+A4×立功+A5×退赃退赔+A6×认罪态度+A7×前科+A8×累犯+……+A14×扒窃）=B0+B1×盗窃数额+C0×从犯+C1×初犯+C2×被害人谅解+C3×积极缴纳罚金或财产保证+C4×立功+C5×退赃退赔+C6×认罪态度+C7×前科+C8×累犯+……+C15×扒窃+D0×从犯×盗窃数额+D1×初犯×盗窃数额+D2×被害人谅解×盗窃数额+D3×积极缴纳罚金或财产保证×盗窃数额+D4×立功×盗窃数额+D5×退赃退赔×盗窃数额+D6×认罪态度×盗窃数额+D7×前科×盗窃数额+D8×累犯×盗窃数额+……+D15×扒窃×盗窃数额。

（三）最优调节程式的获取方法

利用盗窃罪的司法数据，根据上述两个理论模型拟合出两个最优回归线性方程。而要比较这两个最优线性回归方程中哪个更具有实践优势，需要用“均值比较”方法进行检验。

检验的具体步骤如下：首先，利用“一般线性回归”方法计算出上述两个理论模型的最优回归方程的系数；其次，计算出两个最优回归方程下的预测宣告刑的数值；再次，计算两个预测宣告刑与实际宣告刑的差的平方和，即残差平方和，残差平方和小的方法效果最佳；最后，还需要检验上述预测宣告刑与实际宣告刑之间的残差平方是否具有显著性差异。检验显著性的方法仍然是成对的均值比较方法。具有显著优势的回归方程，即为最优调节程式。

（四）一般线性回归方程的结果分析

1.复合模式和单一模式中最优回归方程的获取

根据盗窃数额为0～5万元的1 204个记录，和盗窃数额为5万元～40万元的102个记录及盗窃数额为40万元及以上的51个记录，用SPSS中的一般线性回归方法，可以得到表2中的三组六个最优回归方程。

2.盗窃数额为0～5万元的调节程式比较

根据表2的数据可知，对于盗窃数额为0～5万元来说，复合模式的残差平方和9 826.73，小于单一模式的残差平方和9 961.97。但是，残差平方的均值检验中，其显著性检验的sig值为0.263，大于0.05，不具有显著性。也就是说，两种调节程式没有显著差异。复合模式并不优越于单一模式。从而，复合模式应当被排除，单一模式更可取。

3.盗窃数额为5万元～40万元的调节程式比较

根据表2的数据可知，对于盗窃数额5万元～40万元来说，复合模式的残差平方和12 752.03，小于单一模式的残差平方和13 422.11。但是，残差平方的均值检验中，其显著性检验的sig值为0.241，大于0.05，不具有显著性。也就是说，两种调节程式没有显著差异。复合模式并不优越于单一模式。从而，复合模式应当被排除，单一模式更可取。

4.盗窃数额为40万元及以上的调节程式比较

根据表2的数据可知，对于盗窃数额40万元及以上来说，复合模式的残差平方和17 237.91，大于单一模式的残差平方和16 335.36。但是，残差平方的均值检验中，其显著性检验的sig值为0.726，大于0.05，不具有显著性。也就是说，两种调节程式没有显著差异。复合模式并不优越于单一模式。从而，复合模式应当被排除，单一模式更可取。

5.盗窃数额为0～5万元时两种调节程式中调节幅度的计算〔29〕盗窃数额为5万元～40万元以及40万元及以上的情况下，其调节幅度的计算方法和本节一致。由于篇幅限制，不再一一计算。

还原表2中盗窃数额0～5万元的一般线性回归方程，可以得到单一模式的回归方程为：盗窃罪拘役刑或徒刑刑期=（4.542+0.000549×盗窃数额）（1-0.317×从犯-0.317×自首-0.046×坦白-0.149×被害人谅解+0.233×累犯-0.683×其他从轻情节+0.696×其他从重情节+0.04×入室盗窃）+1.082×从犯+0.569×自首-0.308×坦白-0.183×被害人谅解+1.369×累犯+5.128×其他从轻情节-3.571×其他从重情节+0.854×入室盗窃-1.042×立功-1.715×积极缴纳罚金或财产保证-0.640×退赔退赃+0.730×前科+0.285×携带工具+1.014×扒窃。

从上式可以得出，利用1 204个记录得到的盗窃数额为0～5万元的单一模式中，各量刑情节的调节比例和数值如下：从犯为-31.7%（+1.082），自首为-31.7%（+0.569），坦白为-4.6%（-0.308），被害人谅解为-14.9%（-0.183），累犯为 +23.3%（+1.369），其他从轻情节为-68.3%（+5.128），其他从重情节为+69.6%（-3.571），入室盗窃为+4.0%（+0.854）。其他量刑情节为“固定数值”的调节幅度：立功为（-1.042），积极缴纳罚金或财产保证为（-1.715），退赔退赃为（-0.640），前科为（+0.730），携带工具为（+0.285），扒窃为（+1.014）。所有数值的单位均为月。

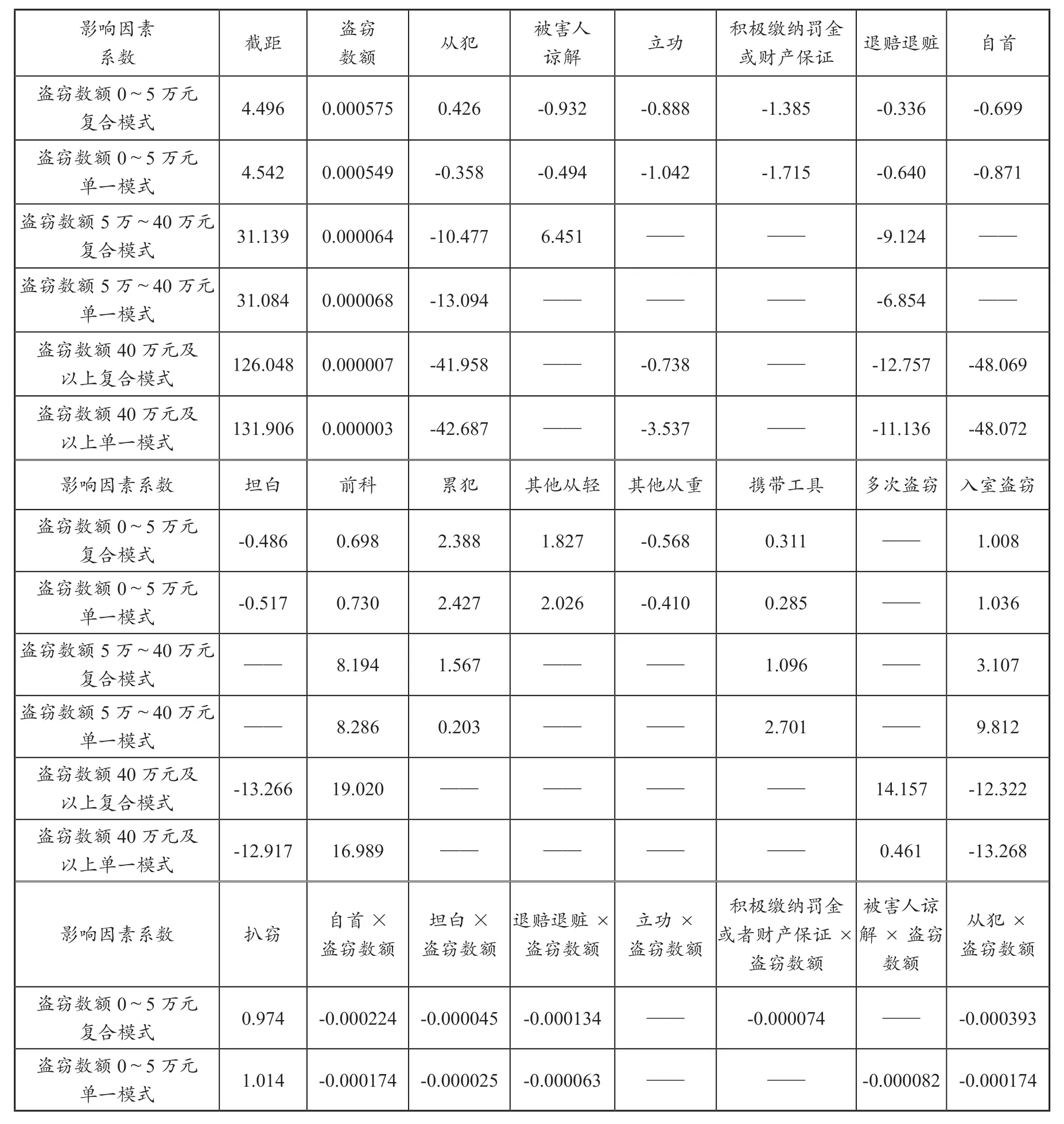
表2 复合模式与单一模式对比研究

（续表）

同理，还原表2中的回归方程，可以得到盗窃数额为0～5万元的复合模式的调节程式为：盗窃罪拘役刑或徒刑刑期=（4.496+0.000575×盗窃数额）（1-0.683×从犯）（1-0.557×退赃退赔-0.005×自首-0.334×坦白+0.092×入室盗窃）+（4.496+0.000575×盗窃数额）（+0.323×退赃退赔-0.384×自首+0.256×坦白-0.050×入室盗窃-0.129×积极缴纳罚金或财产保证+0.268×累犯-0.579×其他从轻情节+0.750×其他从重情节）+0.716×退赃退赔+1.409×自首-0.135×坦白+0.819×入室盗窃-0.803×积极缴纳罚金或财产保证+1.183×累犯+4.430×其他从轻情节-3.122×其他从重情节-0.932×被害人谅解-0.888×立功+0.698×前科+0.311×携带工具+0.974×扒窃-1.710×退赃退赔×从犯-0.015×自首×从犯-1.026×坦白×从犯+0.283×入室盗窃×从犯-1.859×累犯×从犯。

从上面的回归方程还原式可以看出，只有一部分量刑情节（这里包括退赃退赔、认罪态度、入室盗窃情节）能够被纳入连乘式中。大部分量刑情节必须通过“比例固定”和“数值固定”相结合的单一模式对基准刑进行调节。

（五）调节程式比较的结论

本文的数据显示，在盗窃数额为0～5万元的盗窃罪中，以及盗窃数额为5万元～40万元和40万元及以上的盗窃罪中，复合模式均没有明显优于单一模式。所以，现有的《量刑指导意见》中的复合调节程式并不具有优越性，不可取。

四、基准刑调节方法的完善

本文主要讨论基准刑调节方法的完善，但会涉及量刑情节的区分和选取，以及基准刑的确定，因为这些内容将影响到基准刑调节方法的确定。

（一）确立“比例固定”与“数值固定”相结合的调节幅度模式

根据实证分析，通过两种调节幅度模式的比较，可以得出如下结论。

1.纯粹的“比例固定”模式不可取

第二部分和第三部分的数据显示，纯粹“比例固定”模式不能与理论上从轻从重的处罚原则契合。

如前所述，当用第二部分的盗窃数额为0～5万元的770个盗窃罪记录进行一般线性回归，将所有交互效应项都纳入回归方程时，前科、携带工具本是从重情节，却从轻处罚；而立功、退赔退赃、其他从轻情节本是从轻情节，却从重处罚。所以纯粹的“比例固定”模式不可取。

2.“准比例固定”模式与“数值固定”模式处于并存状态

表1的数据得出，对于盗窃数额为0～5万元和5万元～40万元的犯罪来说，“准比例固定”的模式要优于纯粹“数值固定”的模型，而对于盗窃数额为40万元及以上的犯罪来说，“数值固定”模型更为可取。表2的数据可以看出，在盗窃数额为0～5万元、5万元～40万元以及40万元及以上的犯罪中，单一模式的表现形式也是 “准比例固定”模式。可见，“准比例固定”模式虽然是主要的调节幅度模式，但是“数值固定”模式也在有的调节幅度和调节情节中得到应用。

根据司法数据的不同，“准比例固定”模式与“数值固定”模式均可能成为最优调节幅度模式。所以，建议将来《量刑指导意见》中的调节幅度模式不要“一刀切”地采取某一种模式，而应根据司法数据，分情况制定不同的模式。

3.调节比例与调节数值的计算

调节幅度模式应当采取“比例固定”和“数值固定”相结合的方法。但问题是，哪些量刑情节采取“比例固定”方法，哪些量刑情节采取“数值固定”方法，以及具体的调节比例和调节数值如何确定。

（1）盗窃数额为0～5万元的犯罪中调节比例和调节数值的确定

本文共得到两个盗窃数额为0～5万元的最优回归方程：一个是样本量为770个记录的表1中“准比例固定”模式的最优回归方程；一个是样本量为1 204个记录的表2中单一模式的最优回归方程。这两个最优回归方程得到的各个量刑情节的调节比例和调节数值并不相同。表1中“准比例固定”模式的最优回归方程得到数据为：被害人谅解的调节比例为-14.1%（+0.580），积极缴纳罚金或财产保证的调节比例为-27.4%（+1.126），退赔退赃的调节比例为-7.5%（-0.319），自首的调节比例为-49.2%（+2.022），坦白的调节比例为-22.9%（+0.941），其他从重情节的调节比例为58.7%（-2.413），累犯的调节数值为+2.684个月，前科的调节数值为+0.882个月。

表2中单一模式的最优回归方程得到各量刑情节的调节比例和数值如下：从犯为-31.7%（+1.082），自首为-31.7%（+0.569），坦白为-4.6%（-0.308），被害人谅解为-14.9%（-0.183），累犯为+23.3%（+1.369），其他从轻情节为-68.3%（+5.128），其他从重情节为 +69.6%（-3.571），入室盗窃为+4.0%（+0.854）。其他量刑情节为“固定数值”的调节幅度：立功为（-1.042），积极缴纳罚金或财产保证为（-1.715），退赔退赃为（-0.640），前科为（+0.730），携带工具为（+0.285），扒窃为（+1.014）。

对比两个最优回归方程的调节比例和调节数值，发现同一量刑情节的调节幅度模式、调节幅度数据均不相同。那么，如何确定一个犯罪中，各个量刑情节对基准刑的调节幅度模式和调节幅度数据呢？

对于调节幅度模式，应当选择多数最优回归方程得到的模式。如上述两个最优回归方程中，累犯的调节方式不相同。表1的调节模式为“数值固定”模式，调节数据为（+2.684）个月。表2的调节幅度模式为 “准比例固定”模式，调节数据为+23.3%（+1.369）个月。在只有两个最优回归方程的情况下，我们当然不好选择“准比例固定”模式还是“数值固定”模式。但是，当我们进行多次回归后，得到多个最优回归方程的情况下，就可以选择多数最优回归方程得到的调节幅度模式。假设，我们对盗窃数据为0～5万元的数据进行了10次一般线性回归，从而得到10个最优回归方程。这10个最优回归方程中，有7个最优回归方程中，累犯均采取“准比例固定”调节幅度模式，那么，我们就认为，在0～5万元的盗窃罪中，累犯应当选择“准比例固定”调节幅度模式。

确定好调节幅度模式后，调节幅度数据则应当根据所有数据的均值进行确定。例如，上述两个最优回归方程中，被害人谅解的调节幅度数据分别为-14.1%（+0.580）个月和-14.9%（-0.183）个月。那么，我们最终确定0～5万元盗窃罪中，被害人谅解的调节幅度数据则为两者的平均值，即-14.5%（+0.197）个月。当然，通常我们需要用多个最优回归方程的数据来进行平均数的计算，而非两个最优回归方程的数据。

假设，我们分别用10组不同的数据对盗窃罪0～5万元的最优回归方程进行拟合，得到10个最优回归方程。其中7个显示，被害人谅解的调节幅度应当为“准比例固定”模式，且7个数据分别 为 -14.1%（+0.580）、-14.9%（-0.183）、-33.1%（+1.235）、-26.5%（+3.075）、-44.8%（-3.671）、-29.8%（+2.873）、-38.6%（+3.280）。那么，我们可以得出结论，盗窃数额为0～5万元的盗窃行为中，被害人谅解的调节幅度应当采取“准比例固定”模式，其调节比例为上述7个数据的平均值，即-28.8%（+1.027）。

（2）不同法定刑幅度、不同罪名中同一量刑情节调节幅度的确定

用上面的方法可以确定同一罪名同一法定刑幅度中同一量刑情节的调节幅度。那么，同一罪名中，不同法定刑幅度，或者不同罪名中，同一量刑情节的调节幅度如何确定呢？它们的调节幅度是否固定不变呢？

如果通过多次线性回归得到的多个最优回归方程中，不同法定刑幅度、不同罪名中同一量刑情节调节幅度的均值处于比较集中的数据段，那么可以确定这一数据段为同一量刑情节的固定调节幅度。如果不同幅度、不同罪名中，同一量刑情节调节幅度的均值处于很分散的数据段，那么不能确定它们具有固定的调节幅度，而应该各自确定它们的调节幅度。

（二）调节幅度需要受到责任刑上限的制约

我国量刑规范化形成了一个基本的共识，即刑罚的裁量不能超过责任刑的上限，这是责任主义的基本要求。〔30〕参见张明楷：《责任主义和量刑原理——以点的理论为中心》，载《法学研究》2010年第5期；姜涛：《责任主义与量刑规则：量刑原理的双重体系建构》，载《政治与法律》2014 年第3期；李冠煜：《量刑规范化改革视野下的量刑基准研究》，载《比较法研究》2015年第6期。

1.责任刑上限对调节幅度的限制是刑法学界共识

关于责任刑与预防刑的关系，量刑理论上有点的理论与幅的理论之争。但是，不管是“点的理论”还是“幅的理论”都认可责任刑上限对刑罚幅度的限制。在日本，持有“点的理论”的见解认为，应该在量刑时把行为人的责任作为“上限”，在不超出其范围内，从预防性考虑出发来决定最终刑；持有“幅的理论”的见解认为，把行为人的责任作为量刑“基础”的同时，原则上应该在责任评价的“幅度”内，或者不太脱离责任，加入预防性的考虑来决定最终刑。〔31〕参见［日］城下裕二：《量刑理论的现代课题》增补版，黎其武、赵珊珊译，法律出版社2016年版，第4页。德国认同“点的理论”的学者也指出，在罪责抵偿与个别预防相矛盾时，必须认为，在正确遵守所有法律上的和事实上的规定的情况下，恰恰有一个与每一个行为的严重程度相适应的特定的刑罚。而德国判例则认可“幅的理论”，认为为了达到罪责抵偿和特殊预防之间的平衡和协调，不能具体规定与案件的罪责相适应的刑罚，而只是规定一个刑罚幅度，这一幅度以刑罚能够实现其公正的罪责抵偿的任务为限，然后，再根据刑罚对行为人的再社会化所期望的效果，在罪责的幅度之间确定刑罚。〔32〕参见［德］汉斯·海因里希·耶塞克、托马斯·魏根特：《德国刑法教科书》，徐久生译，中国法制出版社2001年版，第1051-1052页。我国学者张明楷教授也指出，责任刑上限点对刑罚幅度的限制，体现了刑法的人权保障机能与法益保护机能的协调关系。〔33〕参见张明楷：《责任刑与预防刑》，北京大学出版社2015年版，第155页。

2.责任刑上限对调节幅度限制的实现

要实现责任刑上限对调节幅度的制约，只需要在现有量刑步骤的基础上，增加几个特定的步骤即可。

首先，我们可用责任刑情节调节基准刑，形成责任刑上限。其次，用预防刑情节在责任刑上限的基础上，调节基准刑，形成准宣告刑。最后，用准宣告刑与责任刑上限对比，若准宣告刑在责任刑上限之下，则直接将准宣告刑作为宣告刑；若准宣告刑高于责任刑上限，将责任刑上限作为宣告刑。

这一量刑理论和步骤体现在量刑公式中即为：刑罚量=基准刑×（1+责任刑情节1的调节比例+……+责任刑量刑情节n的调节比例）+（从重责任刑情节的调节数值-从轻责任刑情节的调节数值）+基准刑×（1+预防刑情节1的调节比例……+预防刑量刑情节n的调节比例）+（从重预防刑情节的调节数值-从轻预防刑情节的调节数值）。在具体计算时，先计算出前面责任刑情节的数值，再计算总的数值，然后拿总的数值与责任刑情节的数值比较，取较小的那一个即可。

例如，表2中盗窃数额为0～5万元的单一模式模型，可以表述为：盗窃罪拘役刑或徒刑刑期=（4.542+0.000549×盗窃数额）×（1-0.317×从犯+0.04×入室盗窃）+（1.082×从犯+0.854×入室盗窃+0.285×携带工具+1.014×扒窃）+（4.542+0.000549×盗窃数额）×（-0.317×自首-0.046×坦白-0.149×被害人谅解+0.233×累犯-0.683×其他从轻情节+0.696×其他从重情节）+（0.569×自首-0.308×坦白-0.183×被害人谅解+1.369×累犯+5.128×其他从轻情节-3.571×其他从重情节-1.042×立功-1.715×积极缴纳罚金或财产保证-0.640×退赔退赃+0.730×前科）。因为从犯、携带工具、入室盗窃、扒窃等均为责任刑情节，所以先计算出算式（4.542+0.000549×盗窃数额）×（1-0.317×从犯+0.04×入室盗窃）+（1.082×从犯+0.854×入室盗窃+0.285×携带工具+1.014×扒窃）的数值，作为责任刑上限，然后再计算出整个算式的数值，将之与上述责任刑上限作比较，取较小的一个作为宣告刑即可。

就具体案例来说，上述单一模式可以表述如下。例如，（案例8）某盗窃罪案例中，行为人盗窃4万元，且存在从犯、自首、被害人谅解三个情节，则盗窃罪拘役刑或徒刑刑期=（4.542+0.000549×盗窃数额）×（1-0.317×从犯）+1.082×从犯+（4.542+0.000549×盗窃数额）×（-0.317×自首-0.149×被害人谅解）+（0.569× 自首-0.183× 被害人谅解）=（4.542+0.000549×40000）×（1-0.317）+1.082+（4.542+0.000549×40000）×（-0.317-0.149）+0.569-0.183=19.183-11.964=7.219。也就是说，行为人的责任刑是19.183个月，而行为人的准宣告刑是7.219个月，所以应当对行为人处以7.219个月。

（三）确立单一模式的调节程式

1.理论上复合模式应当被排除

在盗窃罪中，量刑情节调节基准刑的调节程式应排除复合模式，选择单一模式，原因如下。

（1）如本文第三部分所示，司法实证数据并没有得出复合模式比单一模式具有显著优势，所以应当排除复合模式的适用。

（2）复合模式中的连乘法使基准刑处于不断变动中，导致基准刑失去“基准”的意义。如第一部分所述，复合模式的连乘法使得基准刑在“修正量刑情节”的调节下处于不断减轻的变动中。这种变动虽然使复合模式符合“罪行轻重不同的被告人如果具有相同的量刑情节，从轻的幅度相同但从轻的刑期可以不同”的量刑规律，但是出现了降低“修正量刑情节”的影响，有违反立法本意的弊端。

（3）复合模式的连乘法使得基准刑在“修正量刑情节”的调节下处于不断减轻的变动中，隔断了一般量刑情节对基准刑的直接作用。

（4）复合模式的连乘法产生了多项交互效应项，将修正犯罪构成量刑情节与一般量刑情节相互关联、相互作用、相互影响，使得问题复杂化。

2.司法实践中单一模式较易被接受

厦门中院的司法实践认为单一模式与复合模式相比较，具有明显的优势，更符合当前审判实际的需要。主要体现在：第一，单一模式在基准刑的确定上简便清晰。复合模式下基准刑的确定还要考虑未遂、从犯、防卫过当等所谓社会危害性情节，不但烦琐复杂，而且容易造成基准刑变动不居的状态。而单一模式下基准刑的确定，仅以基本犯罪事实的拟制既遂状态为依据，不必考虑未遂、从犯等因素对基准刑的影响，使得基准刑确定较为简便清晰，不易产生变数。第二，单一模式因其简便易行更容易为法官所接受。统计数据表明，分别采取两种量刑模式进行试点的思明区法院与集美区法院，因同一时期、同一法院的量刑基本保持均衡，试点前期案件的上诉率、发改率等审判绩效并无明显的差异；而针对法官的问卷调查则表明，单一模式的量刑步骤与传统量刑思路相衔接，操作简便，得到了大多数法官特别是基层法官的认同。〔34〕参见李志远、黄冬阳：《从对立到统一 ——厦门中院量刑规范化改革之路径选择》，载《中国审判新闻月刊》 2009年第41期。