探究一类解析几何最值问题解法
2020-03-17李昌成
李昌成
(新疆乌鲁木齐市第八中学 830002)
一、典型题目

2.(2017年全国高考数学理科Ⅰ卷第10题) 已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( .
A.16 B.14 C.12 D.10
二、试题分析
从高考题题号我们不难发现,这两道题分别是当年全国高考数学理科卷的把关题、重要题.题目综合考查直线和椭圆、抛物线的知识,背景简单,问题朴实,本质相近.学生上手容易,深入难,得高分更难,对学生的运算能力要求较高,若直线方程形式选择恰当,可以大大减小难度.反之,一筹莫展.
三、解法探究
解答此题的一般思路是先求出焦点坐标,再设直线PQ的斜率为k,用点斜式(特殊情况,另行说明)写出直线PQ的方程,然后将直线代入曲线,利用韦达定理、弦长公式求出|PQ|,借助两直线的垂直关系,同理求得|MN|.最后建立四边形PMQN的面积关于k的函数,求其最值,得解.事实上,这种方法学生很难处理最后的函数关系以及最值求解,导致前功尽弃!(有兴趣的老师可以试一试)
通过研究发现,直线标准式参数方程是解决此类与“长度”相关的解析几何最值问题的好办法.
1.介绍直线参数方程
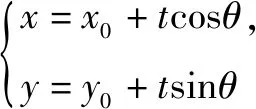

2.应用直线参数方程
例1(2005年全国高考数学理科Ⅱ卷第21题)


整理得(1+cos2θ)t2+2sinθt-1=0,由韦达定理得

由已知得,直线MN与直线PQ垂直,则直线MN的倾斜角为θ±90°,则


评析此法避开了直线斜率存在与不存在引发的讨论.S与θ的函数关系简单明了,思路连贯,解答所用知识都是最重要、最常见,学生易于掌握的的内容.最重要的是最值容易求得.此法有效避开了传统解法的繁杂运算,不失为一种捷解!
例2 (2017年全国高考数学理科Ⅰ卷第10题)

整理得sin2θt2-4cosθt-4=0,
由已知得,直线AB与直线DE垂直,则直线DE的倾斜角为θ±90°,则

所以选A.
例3已知F为抛物线C:y2=2x的焦点,过F作直线l,与C交于A、B两点,则三角形OAB面积的最小值为.

整理得(sin2θ)t2-(2cosθ)t-1=0,



四、总结提升
对于直线与圆锥曲线相交,并且是以长度为基础的最值问题,解答方法较多.其中利用直线的标准式参数方程作答最为简捷.解题步骤是:先找到直线经过的定点,再设定直线的倾斜角,再写出直线标准式参数方程,然后联立直线和曲线,依靠韦达定理,应用参数t的几何意义得到弦长,最后借助三角函数求得最值.
变式题已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点(B,E在第一象限),则四边形ADBE面积的最小值为____.
略解由例2解答知,

一般地,由直线参数方程易得:若MN,PQ是过抛物线y2=2px的焦点F的两条互相垂直的弦,则|MN|+|PQ|的最小值为8p;四边形ADBE面积的最小值为8p2(N,Q在第一象限).
波利亚说过:中学数学教学的首要任务是加强解题训练.但是数学教师如何才能让教学不掉入“题海”之中呢?关键在于对问题的全面深入研究,教给学生最为简捷的方法,使之能成为学生的技能,在解题中能熟练运用!使学生能举一反三,触类旁通.达到“做一题,会一片,懂一类”的效果.只有这样,我们才能保证教学的有效性.
