RC带翼缘剪力墙变形能力计算方法研究

王 斌，史庆轩，蔡文哲，彭一功，李 涵

(1.省部共建西部绿色建筑国家重点实验室/西安建筑科技大学，西安 710055；2.西安建筑科技大学土木工程学院，西安 710055；3.西安建筑科技大学结构工程与抗震教育部重点实验室，西安 710055)

震害调查发现，钢筋混凝土剪力墙变形能力和耗能能力不足是引起高层建筑结构破坏和倒塌的关键因素[1－2]。通过引入基于性能的抗震设计方法可实现对结构反应和破坏程度的有效控制，而其中剪力墙变形能力的准确估算是应用基于位移的抗震设计方法的基础，也是应用能力谱法进行性能评估的关键。

对于RC剪力墙变形能力的计算，最早且应用最广的是由Paulay和Priestley[3]提出的集中塑性铰模型，用该模型可较好地预测混凝土构件的非弹性弯曲变形，此后该模型被大量应用于以弯曲变形为主的剪力墙的变形计算和性能设计[4－5]。然而塑性铰模型的缺陷在于无法考虑剪切变形和滑移变形的贡献，因此在塑性铰模型的基础上，结合Park和Paulay[6]提出的桁架模型来计算剪切变形成为普遍采用的方法。吕西林等[7]和梁兴文等[8]分别依据此方法推导出了RC剪力墙和纤维增强混凝土剪力墙考虑剪切和弯曲变形贡献的极限位移计算公式。但在应用桁架模型计算剪切变形时，假定剪切刚度在整个塑性阶段为一定值，这样剪切变形在构件屈服后基本保持不变，这与实际观测到的试验结果存在显著差异。

在结构平面布置时，一字形墙通常较少单独出现，而是被组合成不同截面形式的带翼缘剪力墙。此类构件由于具有较强的抗弯能力，剪切变形势必会产生较大影响。国内外大量试验研究均表明[9－13]，发生弯曲破坏的带翼缘剪力墙，其剪切变形可超过总变形的15%，并且在剪力墙屈服后其剪切变形随着弯曲变形的增大而增大。因此无论是忽略剪切变形和支座处滑移变形的贡献；亦或是将剪切刚度假定为一常量，都将低估剪力墙的变形能力。

为了更准确地描述剪力墙的变形特性，Dazio[14]通过试验发现，剪切与弯曲变形比在整个塑性阶段近似保持一定值，Hines[15]根据此发现建立了基于“扇形”区弯曲位移的剪切位移的计算公式。Beyer等[16]根据莫尔圆理论中剪应变与平均轴向应变的关系得到了剪切位移与弯曲位移比的计算公式，并结合塑性铰模型建立了弯曲破坏RC剪力墙极限位移的计算公式。但此类计算方法中，需通过计算裂缝倾角来确定剪切位移与弯曲位移之比，无疑增大了计算结果的不确定性。此外，为了反映弯曲变形与剪切变形间的耦合作用，Mostafaei和Vecchio[17]基于修正压力场理论提出了单轴弯剪模型(USFM模型)。梁兴文等[18]成功将USFM模型应用到纤维混凝土剪力墙变形能力的计算中，提出了考虑轴力-弯矩-剪力相互作用的高性能纤维增强混凝土剪力墙荷载-变形模型。但该模型计算工作量较大且编程难度高，只适用于分析计算。因此，如何准确预测剪力墙的各变形分量，建立一种兼顾精度和效率的实用计算模型，是性能设计时亟待解决的问题。

为此，本文依据RC带翼缘剪力墙的变形发展规律，以截面弯矩-曲率分析为基础，分别建立墙肢弯曲变形、纵筋滑移引起的墙肢刚体转动变形以及剪切变形的计算方法，并据此提出一种全新的考虑弯曲、纵筋滑移和剪切变形贡献的RC带翼缘剪力墙荷载-变形分析模型，

1 带翼缘剪力墙变形性能试验研究

1.1 试件概况

为了研究边缘构件约束情况对带翼缘剪力墙破坏机理和变形性能的影响，设计制作了3个T形截面RC剪力墙，对其进行拟静力加载试验，各试件的设计参数见表1。试件高2200 mm，腹板截面尺寸为1000 mm×100 mm，翼缘尺寸截面为900 mm×100 mm，试件截面尺寸及配筋如图1所示。采用C35商品细石混凝土一次性浇筑完成，实测混凝土轴心抗压强度30.68 MPa，钢筋的物理力学性能如表2所示。

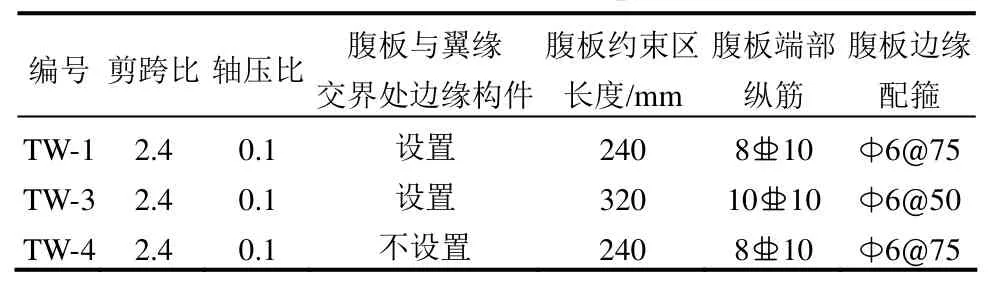
表1 试件参数Table 1 Parameters of specimens

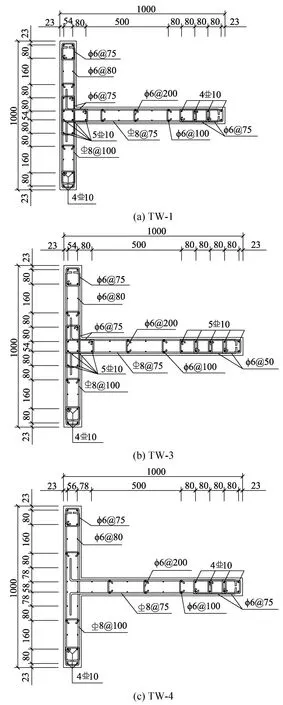
图1 截面尺寸及配筋Fig.1 Dimensions and reinforcement of cross-sections

试验采用悬臂式加载装置，试件基础板通过压梁锚固在刚性台座上以限制基础转动，并通过刚性台座上的抗剪螺栓限制基础平动。由液压千斤顶施加竖向轴压力，并通过一个100 kN的电液伺服作动器沿截面几何对称轴施加水平反复荷载。直至试件在推拉方向承载力均下降到峰值荷载的85%后停止加载，具体的加载装置如图2所示。

表2 钢筋力学性能Table 2 Mechanical properties of steel bars

图2 试验装置Fig.2 Test setup

为了实现剪力墙变形过程的准确量测及各变形分量的合理筛分，在传统的位移计和应变片测量的基础上，本次试验引入高精度无干扰测试手段—粒子图像测速(PIV)技术，具体的测试方法和变形计算过程详见文献[19]。

1.2 试验破坏形态

3个试验试件均发生弯曲破坏，但由于翼缘提供了较强的抗弯能力，试件也表现出了一定的弯剪破坏特征。试件的裂缝主要包括水平弯曲裂缝、弯剪斜裂缝和竖向劈裂裂缝。其中水平弯曲裂缝在加载初期便已产生，主要分布在翼缘外表面和腹板自由端底部1.5 m高度范围内。弯剪斜裂缝一部分是由腹板自由端的水平裂缝斜向延伸形成，另一部分分布在腹板约束端，两者在腹板中下部形成明显的“X形”交叉裂缝。竖向劈裂裂缝出现在加载中后期，集中于腹板自由端根部，随即该处混凝土保护层脱落，纵筋和箍筋外露。在弯矩和轴压力的共同作用下，试件的破坏同样放生在腹板自由端根部，该处边缘构件内纵筋全部压屈，核心混凝压酥，箍筋受拉屈服，在反向加载时最外层纵筋被拉断，试件丧失承载力。各试件的最终破坏形态如图3所示。

图3 试件破坏形态Fig.3 Failure modes of specimens

1.3 变形分量全过程分析

图4给出了3个试验试件各变形分量与总变形之比在加载过程中的变化规律。可以看出，墙肢与基础间的滑移变形在加载初期不超过总位移的10%，在构件进入塑性阶段后，滑移变形所占比重逐渐减小。在翼缘受拉方向滑移变形小于总位移的3%，而翼缘受压方向滑移变形只占总位移1%左右，因此在变形能力计算时可忽略滑移变形的贡献。剪切变形在加载初期所占比重较高，随着墙肢底部水平弯曲裂缝的不断形成，弯曲变形开始加速增长。构件屈服后，剪切变形与弯曲变形基本保持同步增长的态势。从而可知，对于以弯曲破坏为主的T形墙，在其抗剪机制并未严重损伤的情况下，其剪切变形与总位移之比在整个塑性阶段基本保持一定值。同时T形墙的剪切变形达到了总位移的15%左右，因此在变形能力计算时应计入剪切变形的贡献。

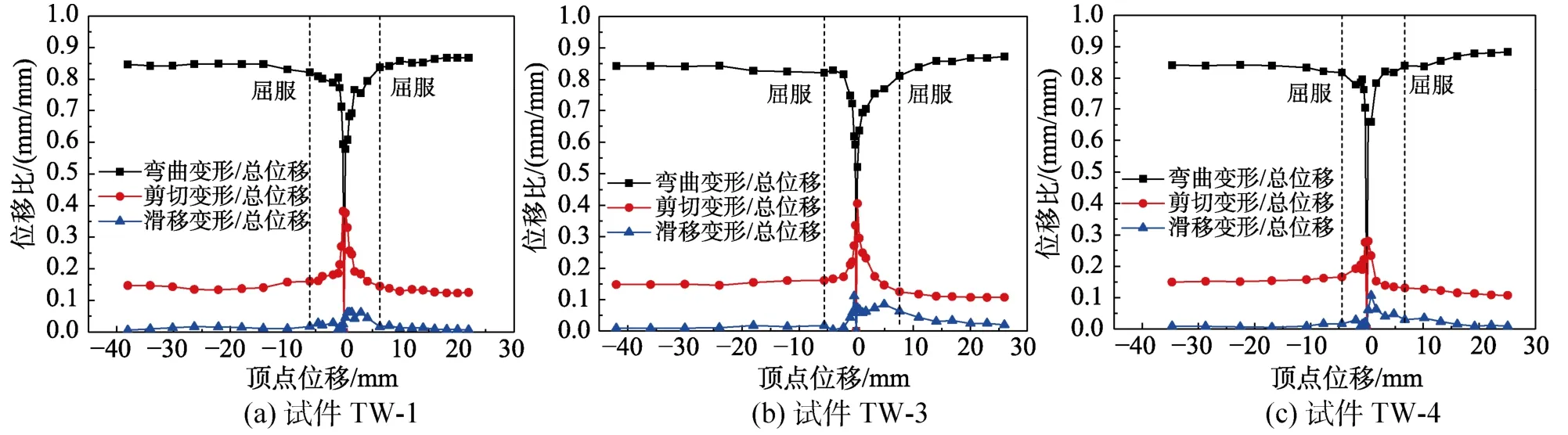
图4 各变形分量与总位移之比Fig.4 Ratios of each deformation component to total top displacement

2 弯曲变形的计算

剪力墙的弯曲变形Δf是由墙肢的弯曲变形Δf,f和纵筋滑移引起的墙肢刚体转动所产生的变形Δf,θ组成，下面就两者分别建立模型。

2.1 墙肢弯曲变形

对于一给定荷载的剪力墙构件，其沿墙高的弯矩分布是已知的，从而根据弯矩-曲率关系可得到沿墙高的曲率分布，对曲率沿墙高积分两次就可得到剪力墙的弯曲位移。该计算方法思路清晰，计算简便，但在峰值荷载后应用该方法会产生较大误差。这是由于峰值荷载后沿墙高的弯矩值会减小，在底部截面的曲率超过弯矩-曲率曲线的峰值点后，塑性铰区内根据弯矩值反算得到的曲率值远小于试验值，从而低估了剪力墙的弯曲位移。而集中塑性铰模型通常假定等效塑性铰区高度在塑性阶段保持不变，根据屈服和极限状态下的位移值得到双线形的荷载-位移曲线，这与构件的实际推覆曲线也存在较大差异。

综合上述两种方法的利弊，本文采用基于弯矩-曲率分析的分段式计算方法，并考虑塑性铰区高度的变化。对于顶部受一水平集中荷载的情况，水平剪力可直接通过弯矩与构件高度之比得出，而位移分为屈服前和屈服后两阶段计算。构件屈服前，曲率沿墙高基本呈线性分布，墙肢弹性弯曲位移Δef,f可直接按式(1)计算：

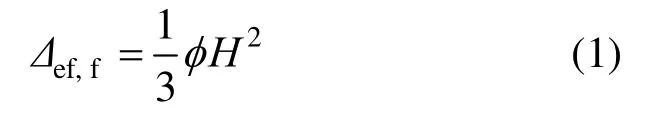
式中：ϕ为墙肢底部截面的曲率；H为剪力墙总高度。

构件屈服后，墙肢弯曲位移采用塑性铰模型计算，即认为顶点位移由弯曲屈服位移Δyf,f和弯曲塑性位移Δpf,f组成，但等效塑性铰区高度不再假定为一定值，根据图5所示的双线形曲率分布，可得到等效塑性铰区高度lp的计算表达式：

式中：为塑性铰区高度；M和My分别为底部截面的实时弯矩和屈服弯矩。在构件达到峰值荷载后，根据试验观测到的现象，认为塑性铰区高度不再发生变化，即采用峰值荷载时的等效塑性铰区高度来计算峰值荷载后的位移，并参考文献[15]将塑性转动中心设定在墙肢底部，塑性阶段墙肢弯曲位移计算公式如下：

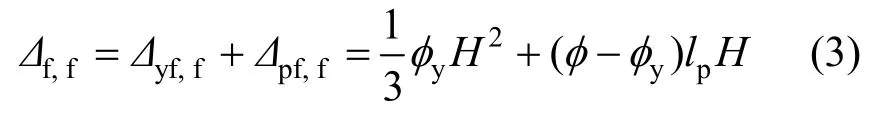
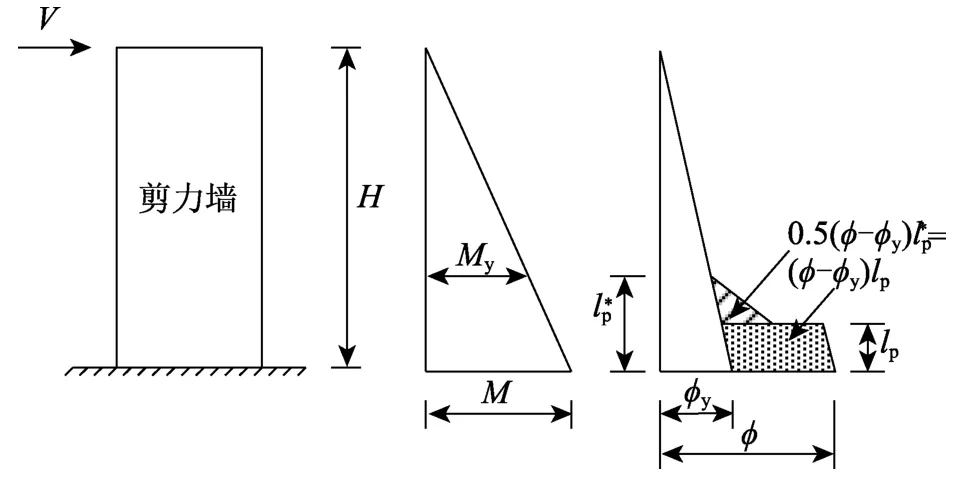
图5 塑性阶段弯矩与曲率分布Fig.5 Distribution of moment and curvature in plastic range

2.2 纵筋滑移引起的弯曲变形

对于纵筋滑移引起的变形计算，以往通常在塑性铰模型中通过增大塑性铰区高度来实现，但此举一来概念模糊，大多是根据经验取值；二来未能体现纵筋滑移量随位移增大而增大的特征。因此本节采用独立的模型来计算纵筋滑移引起的变形，具体依照受拉钢筋端部的滑移量与中和轴高度来计算，如图6所示，表达式如下：

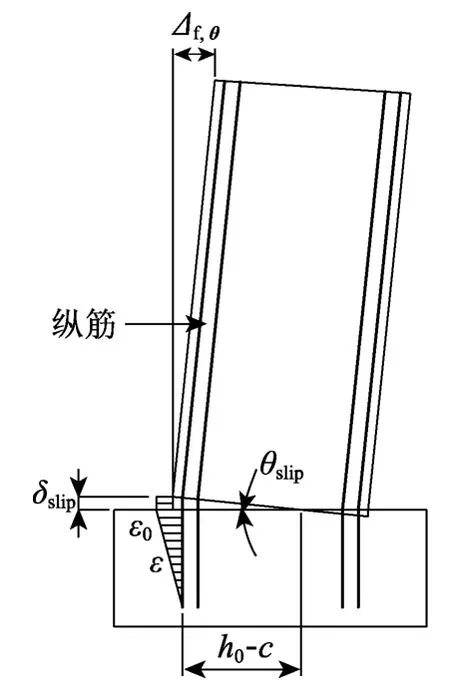
图6 纵筋滑移的计算模型Fig.6 Models for calculating slip of longitudinal bars

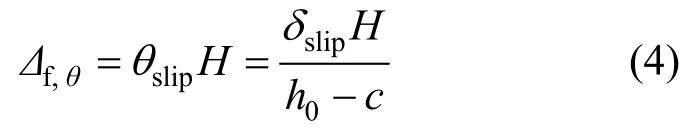
式中：θslip为纵筋滑移引起的墙体转角；δslip为锚固区内受拉纵筋的滑移量；h0为截面有效高度；c为中和轴高度。

中和轴高度可直接从截面分析中得出，而锚固区内纵筋的滑移量依照Lowes和Altoontash[20]提出的模型计算，并在该模型的基础上做了两点简化：首先锚固长度la以纵筋屈服时的长度为准，并假定la不随荷载的增大而变化；其次对于给定荷载状态下，锚固长度内应变ɛ假定为线性分布。图7分别给出了实际应变分布以及本节简化模型假定的应变分布图，可以看出简化模型高估了屈服前的滑移变形，低估了屈服后的滑移变形。但考虑到实际应变分布需要通过在纤维模型中添加零长度界面单元或者在三维实体模型中添加弹簧单元计算得出，建模和计算过程较为复杂，而采用Lowes模型每一步仍需要计算大量的参数，虽然简化模型牺牲了一定的精确度，但计算过程得到了很大程度的简化。通过对比计算发现两者在翼缘受压方向的误差相对较大，但基本符合设计精度的要求。

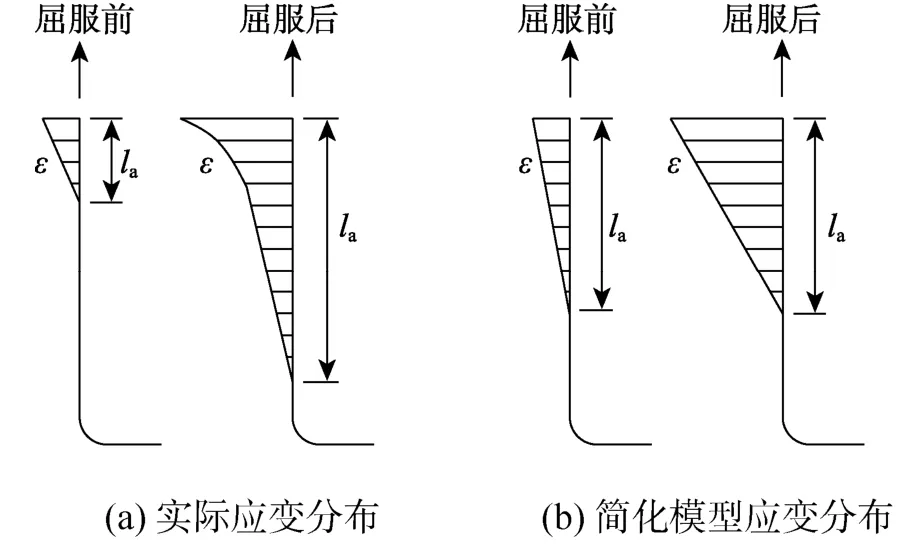
图7 锚固区内的应变分布Fig.7 Strain distribution in anchorage zone

根据应变三角形分布的假设，可得到纵筋滑移量的计算式：

式中：ɛ0为给定荷载下试件底部受拉钢筋的最大应变，可由截面分析得出。计算锚固长度时，参照Eligehausen等[21]的建议将钢筋的平均粘结应力τavg假定为一常量，即并根据钢筋拔出力与锚固力的平衡条件来计算锚固长度，即：

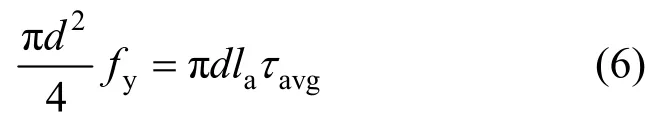
换算即可得到屈服时锚固长度的计算表达式：

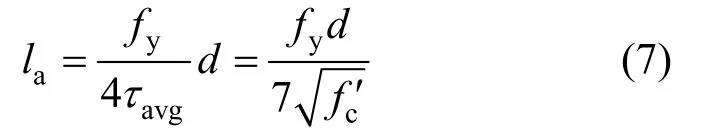
式中：d为纵筋直径；fy为受拉钢筋屈服应力；为混凝土圆柱体抗压强度，可由试验测得的立方体抗压强度换算得到。

将式(5)和式(7)代入式(4)中，即可得到纵筋滑引起的弯曲位移：

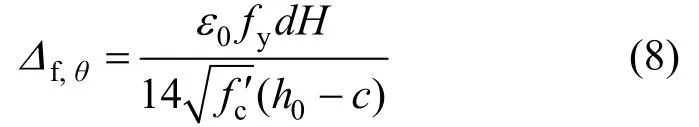
计算滑移变形全曲线时，d、fy、f′、H、h0均为常量，只需将弯矩-曲率分析中每一荷载步的最大钢筋应变ɛ0和中和轴高度c代入即可。

2.3 试验验证

将墙肢的弯曲变形Δf,f与纵筋滑移引起的变形Δf,θ相加即可达到带翼缘剪力墙的总弯曲变形Δf，图8分别给出了试件TW-1、TW-3和TW-4计算与试验得到的荷载-弯曲变形骨架曲线对比图。

由图8可知，采用本节建立的模型计算出的荷载-弯曲变形骨架曲线与试验实测曲线吻合良好，两者承载力的差值在1%以内，只是计算曲线的上升段刚度略大于试验曲线，且翼缘受拉方向的极限位移普遍小于试验值。这主要是因为计算时忽略了剪切裂缝对弯曲变形的影响，剪切裂缝的存在不仅会降低构件的弯曲刚度，也会增大塑性铰区高度，致使剪力墙的实际变形大于计算位移。至于翼缘受压方向，试验试件的破坏是由腹板自由端压屈后的纵筋拉断控制的，由于分析模型只能计算出单调曲线，无法对压屈后纵筋的极限拉应变做出准确估计，只能依据文献[22]近似取为钢筋极限拉应变的0.75倍，因此极限位移略大于试验值。但总体来看，本节所建立的弯曲分析模型能较好地预测带翼缘剪力墙的受弯响应，且计算结果已达到相当的精度，可认为该弯曲变形计算模型是有效的。

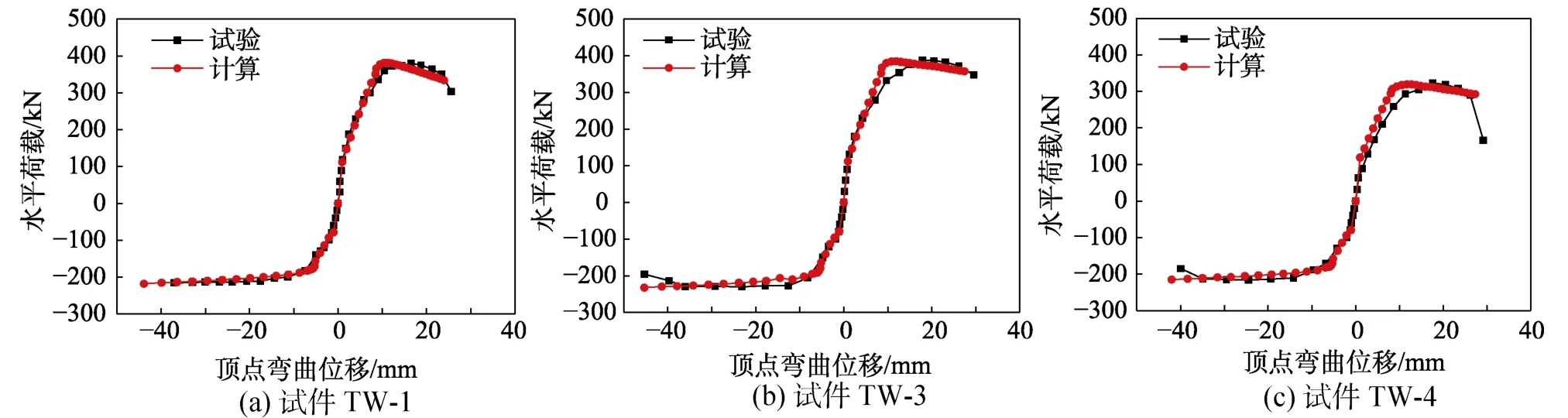
图8 计算与试验荷载-弯曲变形骨架曲线对比图Fig.8 Comparison of load- flexural deformation skeleton curves between experimental and analytical results.

3 剪切变形的计算

鉴于桁架模型无法考虑塑性阶段剪切刚度的退化，而剪切与弯曲变形比的经验计算式又过分依赖于所选取的试验数据，缺乏理论支撑。因此本节将两者结合起来提出一种全新的剪切变形计算方法，既能发挥桁架模型的理论优势，又能考虑剪切与弯曲变形比在塑性阶段保持不变的特征。

3.1 模型的建立

本节就剪切变形分为屈服前和屈服后两阶段分别计算。构件屈服前，可直接根据弯矩曲率分析得到的荷载值，采用剪切变形的弹性计算公式计算剪力墙的顶点剪切位移，即：

式中：he为弹性区域的高度，即剪力墙总高度H减去塑性区域高度；G分别为混凝土的弹性模量和剪切模量；Aw为剪力墙腹板截面面积；μ为截面形状系数，对于本文研究的T形截面剪力墙，根据截面几何尺寸取μ=2.0375[23]。

剪力墙屈服后，沿墙肢高度方向曲率呈非线性分布，顶点弯曲位移主要由塑性铰区转角产生，由于弯曲损伤与剪切变形间的相互作用，即使沿墙高方向剪力是不变的，但剪切变形也主要集中于塑性铰区内。Brueggen[24]通过对比T形墙沿墙高方向的曲率分布与剪应变分布发现，两者的分布规律一致，归一化处理后两者曲线基本重合，这说明了剪应变与曲率之间存在线性关系。Beyer等[16]通过对U形墙沿墙高方向的剪应变测量发现，不同高度处剪应变的大小与受拉钢筋的应变相关，说明了剪应变与纵筋拉应变之间存在线性关系，鉴于中和轴高度在塑性阶段基本保持不变，将纵筋拉应变除以受拉区高度即可换算成曲率，因此同样可得出剪应变与曲率之间存在线性关系的结论，两者间的比例关系表示如下：

式中：C为剪应变γ与曲率ϕ间的比例常数，量纲为长度。对式(10)两侧积分，即可得到剪切位移Δs与弯曲转角θf间的比例关系：

因此只要确定了C值的大小，就可根据述弯曲变形计算得到的转角θf来计算塑性阶段的剪切位移。

由材料力学的物理关系可知：

式中：EI为抗弯刚度；Ks为单位长度内的剪切刚度；M和V分别为弯矩和剪力，两者之比为剪力墙的高度H，即：

将式(12)、式(13)和式(14)代入到式(10)中，可得到比例常数C的表达式：

由于剪切变形与弯曲变形之比在整个塑性阶段保持不变，因此可认为比例常数C在构件屈服后保持一定值。选取屈服时的剪切刚度与弯曲刚度来计算常数C，其中单位长度内的剪切刚度Ks可根据桁架模型[5]计算：

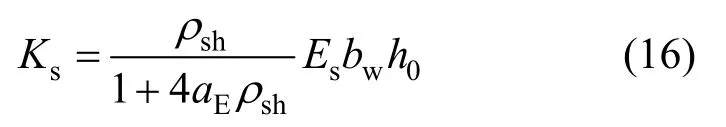
式中：ρsh为水平抗剪钢筋配筋率；bw为剪力墙腹板截面宽度；aE为钢筋弹性模量Es与混凝土的弹性模量Ec之比，考虑到构件在损伤后，混凝土斜压杆软化会造成aE的增大，根据Priestley等[22]的建议，对aE取平均值10。屈服时的弯曲刚度EI可直接根据弯矩曲率分析得到的屈服弯矩My和屈服曲率ϕy确定，从而(15)可表示为：

代入式(11)中，即可得到塑性阶段剪切位移Δs的计算表达式：

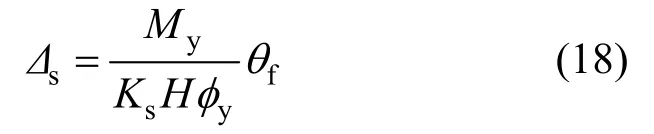
3.2 试验验证

图9分别给出了试件TW-1、TW-3和TW-4计算与试验得到的荷载-剪切变形骨架曲线对比图。可以看出，应用本节建立的模型计算得到的荷载-剪切变形骨架曲线，其上升段刚度、走势以及峰值荷载对应的位移均与试验实测曲线吻合良好，只是极限剪切位移与试验值略有出入。对于翼缘受拉方向，极限位移的计算值均大于试验值，这是由于在剪切变形计算时，假定剪切与弯曲变形之比在整个塑性阶段保持不变，而由图4可知，该假定对于翼缘受压方向完全成立，但在翼缘受拉方向剪切与弯曲变形之比在整个塑性阶段呈不断减小的趋势，虽然减小程度较小，但该假定仍会一定程度上高估剪切变形。对于翼缘受压方向，极限位移的计算值均小于试验值，这是由于试验试件在该加载方向经历倒数第二级循环时，腹板自由端最外侧纵筋已被拉断，此后又经历了一级循环直至第二排纵筋被拉断才宣告试验结束，而计算时极限状态被定义为最外侧纵筋达到极限拉应变，如果与倒数第二级循环时的实测值相比较，结果基本吻合。但总体来看，本节所建立的剪切变形计算模型能较好地反映带翼缘剪力墙的剪切变形性能，验证了该模型的有效性。

图9 计算与试验荷载-剪切变形骨架曲线对比图Fig.9 Comparison of load-shear deformation skeleton curves between experimental and analytical results.

4 模型验证与评价

在完成了弯曲、纵筋滑移以及剪切变形计算模型的建立后，有必要对这三部分变形进行整合，以验证该整合模型的有效性。图10分别给出了试件TW-1、TW-3和TW-4计算与试验得到的荷载-位移骨架曲线对比图。

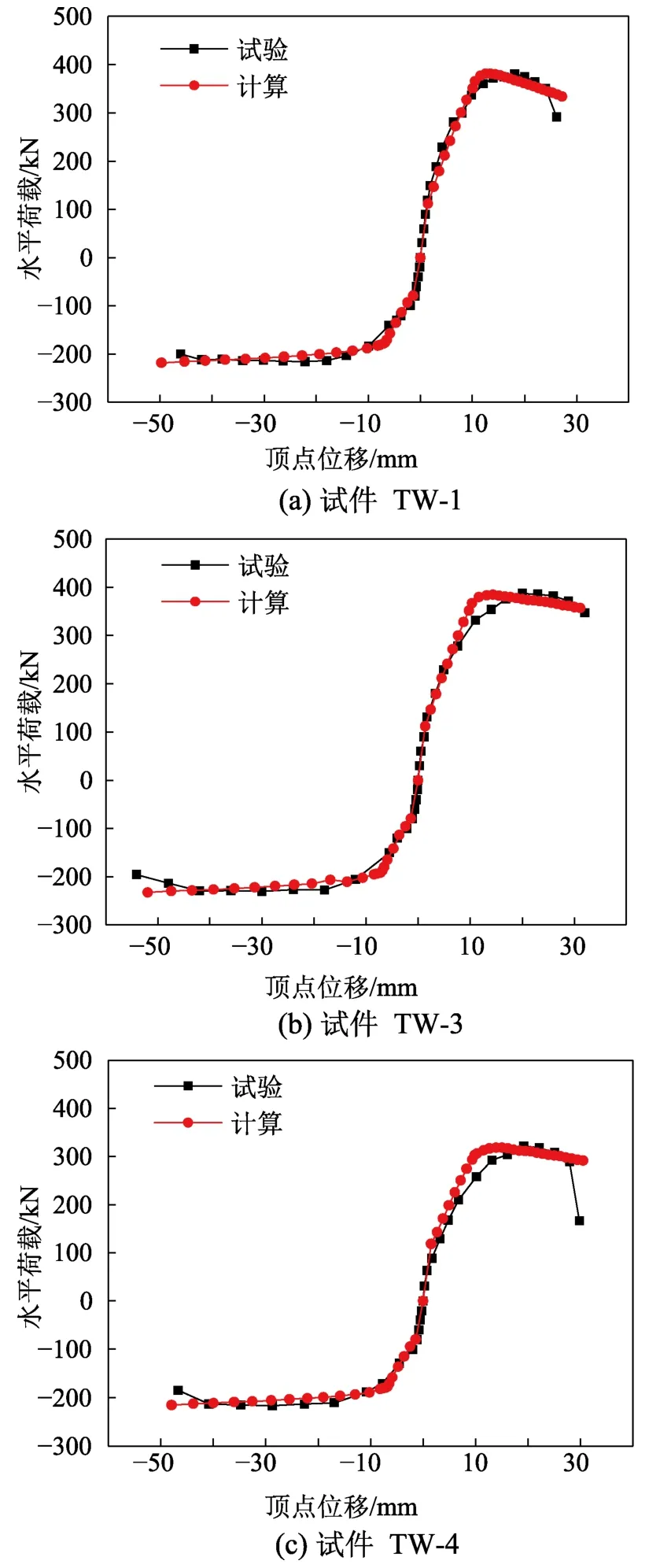
图10 计算与试验荷载-位移骨架曲线对比图Fig.10 Comparison of load-displacement skeleton curves between experimental and analytical results.

由图10可知，将三部分变形整合后得到的荷载-位移骨架曲线与试验骨架曲线吻合良好，说明本文提出的计算模型能较好地预测带翼缘剪力墙的荷载-变形趋势。该模型通过简单的截面弯矩-曲率分析，可综合反映出轴压比、钢筋布置形式。配筋率、配箍率、材料强度及截面几何形状等参数对变形性能的影响。此外，该模型物理意义清晰，变形分量计算明确，可反映出弯曲、剪切、纵筋滑移对总变形的贡献。同时计算过程无须迭代等繁琐的过程，只需将截面的弯矩-曲率分析结果及构件的几何参数和材料属性代入公式计算即可，模型的建立未有过多的简化假设，公式的得出也没有采用拟合等偏经验的方法，保证了模型的准确性和简便性，完全适用于设计人员进行初步设计。

本文提出的荷载-变形分析模型不仅适用于以弯曲破坏为主的非对称截面带翼缘剪力墙，对矩形墙以及其他截面形式的带翼缘剪力墙也同样适用，只是非对称截面剪力墙计算时需要进行正反两方向的弯矩-曲率分析。

传统变形分析模型在计算剪力墙剪切变形时一般采用在弯曲变形的基础上乘以一比例系数。剪力墙任意高度处的弯曲变形可通过曲率积分或塑性铰模型得出，由于剪切变形的侧移形状与弯曲变形并不一致，因此只能通过该比例系数计算剪力墙顶点剪切位移，而将该比例系数应用于其余高度处时，将会低估塑性铰区内的剪切变形，高估弹性区域内的剪切变形。本文模型摒弃了直接将剪切位移与弯曲位移通过比例常数联系起来的经验计算方法，依据曲率与剪应变沿墙高分布一致的规律，以此建立了剪切位移与弯曲转角间的比例关系，因此该模型不仅能得到顶点剪切位移，还能得到层间剪切位移等任意高度处的变形值。由于在应用直接基于位移的抗震设计方法(Direct Displacement-Based Design)时，结构层间位移的计算是性能设计中确定目标位移的关键问题之一，因此，本文提出的变形计算方法具有重要的参考意义。

对于剪力墙变形指标的计算，大多数方法只考虑了极限状态下的量，而若要对结构反应即量化的位移指标进行全面的控制，就应对其受力和变形全过程进行准确的预测。此外，在应用能力谱法进行抗震性能评估时，推覆曲线是建立能力谱曲线的基础，因此采用本文计算模型得到的荷载-位移全曲线为性能设计和性能评估提供了一种有效的分析手段，可供工程设计参考。

5 结论

根据RC带翼缘剪力墙的变形发展规律，以截面弯矩-曲率分析为基础，分别针对墙肢弯曲变形、纵筋滑移引起的墙肢刚体转动变形以及剪切变形建立计算模型：

(1) 采用考虑等效塑性铰区高度变化的集中塑性铰模型计算了带翼缘剪力墙的墙肢弯曲变形，根据简化的Lowes模型得出的纵筋滑移量计算了纵筋滑移引起的墙肢刚体转动变形。将计算所得的总弯曲变形与试验实测曲线进行对比，验证了弯曲分析模型的准确性。

(2) 根据剪应变与曲率间的线性关系，建立了剪切位移与弯曲转角间的比例关系，两者间的比例系数可根据屈服时的剪切与弯曲刚度来计算，将剪切变形计算结果与试验实测曲线进行对比，验证了剪切分析模型的准确性。

(3) 将三部分计算模型进行整合，提出了一种全新的考虑弯曲、纵筋滑移和剪切变形贡献的带翼缘剪力墙荷载-变形分析模型。该模型不但变形分量计算明确，计算过程也无须迭代等繁琐的过程，只需将截面的弯矩-曲率分析结果及构件的几何参数和材料属性代入公式计算即可。同时该模型不仅适用于以弯曲破坏为主的非对称截面带翼缘剪力墙，对矩形墙以及其他截面形式的带翼缘剪力墙也同样适用，本文提出的计算模型为性能设计和性能评估提供了一种有效的分析手段，可供工程设计参考。