饱和地基高填方工程不排水稳定性分析方法研究

谢庄子，程晓辉，刘 伟，麻 强

(1.清华大学土木工程系，北京 100084；2.空军研究院工程设计研究所，北京 100068)

随着我国改革开放的深入、综合国力的增强，各地新建机场的需求旺盛。我国当前在山区在建和已建的高填方机场有数十个，如攀枝花机场、九寨沟黄龙机场、广西河池机场、延安机场、吕梁机场等[1－4]，山区机场突出特点为边坡高差大，如九黄机场填方高度达102 m、河池机场填方高度近80 m、吕梁机场及延安机场达到120 m。由于各高填方机场间地质条件相差很大，无法直接借鉴以往的成功经验，而规程规范对于地基抗剪强度参数约定不一，为工程设计带来了很大困扰。国内高填方工程有成功的经验，也有失败的教训，高填方机场一旦发生滑坡破坏，往往造成数亿元经济损失，甚至直接报废，教训非常惨痛。

2015年某新建山区高填方机场发生边坡破坏，该边坡填方高度约50 m，施工期间坡脚处隆起鼓包，完工后坡顶发生大面积开裂。滑坡治理期间经勘测，认为潜在滑移面出现在原地表下20 m以上的深处，与设计中预测和预防的浅层滑移模式截然不同，事故分析认为可能与地下水的影响有关。如何考虑地下水位较高的饱和地基上的填方稳定性，如何确定饱和地基的不排水强度参数，是规避此类工程风险值得研究的重要工程设计问题。

本文首先介绍3种不排水稳定性分析方法，并讨论各方法之间的异同与应用上的优劣，之后从简单算例入手，说明各方法的分析结果，在此基础上，进行一个拟建工程设计实例的讨论，计算结果表明引入不排水分析后，对于工程设计可能导致的重要影响，并最终给出针对饱和地基上填方工程不排水稳定分析建议采用的强度指标和分析方法。

不同于规程中常见的极限平衡法和当前逐渐被广泛应用的弹塑性有限元法，本文主要采用的计算方法是有限元极限分析方法。通过极限上、下限分析，可以包络真实解并给出误差范围，有效避免了计算方法带来的误差。同时，文中计算结果也与PLAXIS弹塑性有限元分析结果进行了对比验证，保障了结论的正确性。

1 不排水强度指标比较研究

对于不排水边坡稳定性强度参数的确定，有多种试验方法，常用的包括固结排水试验(CD)、固结不排水试验(CU)、不固结不排水试验(UU)等三轴试验，以及快剪、固结快剪等直接剪切试验，除此之外还有工程现场的大型直剪试验、十字板剪切试验等方法。其中，我国CU试验多给出的是Mohr-Coulomb总应力指标，即ccu和φcu，该方法在国外文献中一般被称为Method C，这与国外工程实践普遍采用的基于有效应力的不排水强度指标(Method A)或基于固结应力(埋深)的不排水强度指标(Method B)有较大不同[5－6]。在我国地基基础相关的国家规范、行业标准和地方标准中的规定和解释也不尽相同。如针对填方边坡设计，尽管以下3本规范均规定在不同情况下使用固结不排水试验(CU试验和固结快剪)或不固结不排水试验(UU试验和直剪快剪)确定强度参数，但2种参数应用场景的划分却各有不同：国标《建筑边坡工程技术规范》按土体含水状态划分，规定对粘土选用前者(固结不排水强度参数)，但对饱和粘土选用后者(不固结不排水强度参数)[7]；行标《民用机场岩土工程设计规范》则根据土体强度划分，建议一般情况下均采用前者，对软弱土层采用后者[8]；而2018年起实施的行标《高填方地基技术规范》通过总结过往工程经验，给出了“理论上宜采用原状土固结不排水剪切参数，考虑影响因素的不确定性，从安全角度推荐采用不固结不排水剪切参数”的建议[9]。在《建筑边坡工程技术规范》中还提到了按土水分算原则计算时，宜采用土的有效抗剪强度指标[7]，但对于该指标由何种试验获取，及如何应用在计算中并没有进一步说明。可以说虽然我国通过大量工程实践，积累了一些土体不排水强度参数选用的经验，并写入了规程规范中，但并没有明确区分3种不排水强度指标。

目前我国工程勘察阶段实验室试验鲜有有效应力指标测试，比如含超静孔压测试的固结不排水试验，地勘报告一般给出的是固结不排水总应力指标或固结快剪指标等，这导致目前我国工程实践中不排水稳定性分析多采用Mohr-Coulomb总应力指标。

对于饱和地基上的不排水稳定性分析，国外的设计手册和文献普遍采用有效应力不排水分析方法，如欧洲大陆采用基于有效应力指标的不排水分析方法(Method A)，而英美则建议采用随深度增加的不排水强度指标su进行设计和分析 (Method B)[10－11]。从试验的角度，可以通过原位的十字板剪切试验获得不排水强度参数，但该试验方法对于较硬的地基土难以实施，同时由于土体在自重下的K0固结导致的强度各向异性，十字板剪切试验往往会低估其强度，且由此测得的强度参数对应土体的残余强度[12]。故以往研究者提出了多种基于实验室试验拟合确定不排水抗剪强度su的方法[13－14]。此类方法相较我国工程界的惯常做法，已经更为充分地考虑了地基的不排水效应，但该方法的发展与完善过程中也曾发生过严重的工程事故。2004年新加坡Nicoll Highway地铁站基坑发生严重垮塌事故，该工程设计过程中采用Method A进行不排水抗剪强度su估算，过分高估了地基软弱饱和粘土的不排水强度，被认为是导致该事故的主因之一[15]。在此事故发生后，新加坡规定饱和软土地基上的工程建设在采用Method A估算其不排水强度参数su的同时，都必须辅以试验验证。

可见，针对饱和地基的不排水强度研究对于填方工程稳定性分析而言具有不可忽视的重要意义。针对这一问题，目前国内规程规范几乎没有涉及，工程界对于不排水强度指标和分析方法的选用还缺乏广泛的认识，且国内外均有此类工程事故的先例。

1.1 工程常用方法(Mohr-Coulomb总应力强度指标方法，Method C)

我国现行规程规范中对于地下水的影响，多给出如“验算边坡稳定时，应考虑地下水对边坡稳定的不利影响”的一般规定[16]，而基本没有给出针对不排水问题中超静孔隙水压增长的实用考虑方法。在大量工程设计中，普遍直接使用由固结不排水三轴压缩试验或固结快剪试验确定的固结不排水总应力强度参数ccu和φcu确定Mohr-Coulomb破坏包线进行计算。其应力路径如图1OC线所示，与固结不排水强度包线交于C点。

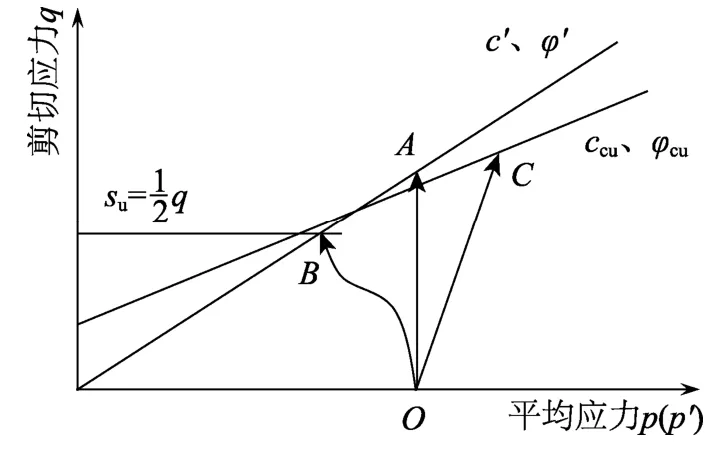
图1 不排水分析方法应力路径对比Fig.1 Comparison of the stress paths of different undrained analysis methods

工程实践和理论分析表明，针对饱和地基上的填方工程设计，应用该方法存在着高估不排水稳定性的风险，其原因主要包含以下四点：首先，在边坡的潜在滑移面上，分为主动受压区、直剪区和被动受压区，如图2所示[17]。对于强度参数设计值的确定，一般依据实验室三轴压缩或直剪试验，但研究和试验均表明，K0固结土存在不排水抗剪强度各向异性[18]，采用三轴压缩试验确定的不排水强度su参数将会高估直剪区和被动受压区的抗剪强度。第二，边坡在发生破坏时需要满足滑移面上的应变协调，由于主动受压区和被动受压区土体抗剪强度的不同，及达到其峰值强度的峰值应变的不同，滑移面上各点并不能同时发挥强度，从而发生滑裂面上压区的强度软化，导致渐进性破坏。第三，应用Mohr-Coulomb总应力准则进行强度分析时，根据Mohr圆与强度包线之间的相切关系可知，破坏面将与最大主压应力方向夹角为45°-φcu/2，与后文讨论的不排水强度指标方法有所不同，进而决定了滑移面形状与位置的差异。第四，由总应力指标表示的Mohr-Coulomb强度由于无法遵循有效应力原理拆分土骨架和孔隙水的受力，被认为理论上不如后文Method A和Method B准确[19]。综合以上可知，采用固结不排水三轴压缩试验或固结快剪试验确定ccu和φcu参数的总应力Mohr-Coulomb指标方法，在应用于饱和地基上快速填方工程时具有高估其安全性的风险。基于以上原因，英美等国早已提出过考虑土体不排水强度各向异性的软土边坡稳定性设计ADP方法(active-direct simple shearpassive)[17]，但该方法应用复杂、需要大量试验数据，在我国鲜有应用，本文也不进一步展开讨论。

图2 边坡内不同位置的破坏模式Fig.2 Failure modes at different locations beneath earth-fill slope

1.2 基于Mohr-Coulomb有效应力指标的不排水分析方法(Method A)

当可以获得地基土体的有效应力指标时(通过实验室试验或其他估算方法获得)，可以采用Method A。该方法假定土体在不排水剪切时有效应力路径垂直向上发展，最终与有效应力破坏包线交于A点，如图1中OA线所示。此时根据土体的有效应力参数和所处应力水平，可以换算该点处的不排水抗剪强度换算公式如下：

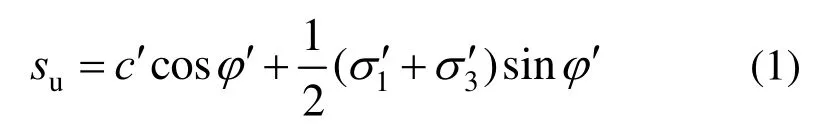
对于非淤泥质、非灵敏性、正常固结饱和软土，假定其有效应力路径垂直向上发展与大量实验室不排水剪切试验真实情况的误差通常在可接受范围内，而且如果假定土体是线弹性的，这种垂直向上的有效应力路径也可由Skempton A系数(=1/3)和B系数(=1)计算获得。Method A原理简单，应用方便，具有一定的优势。由于Method A是将有效应力指标转换为不排水强度包线，即的水平线，因此根据Mohr圆与强度包线之间的相切关系可知，利用该方法时破坏面与最大主压应力夹角为45°。

当仅有固结不排水强度指标ccu、φcu，而缺乏有效应力指标时，可以采用以下方法根据粘土的分类指标估算c'、φ'。对于正常固结土，其粘聚力c'=0，或可以取一小值；研究表明，无论何种土，其有效应力内摩擦角的分布范围与塑性指数Ip之间都存在着较为一致的关系，如图3所示[11]。据此，可以估算土体的有效应力强度指标。

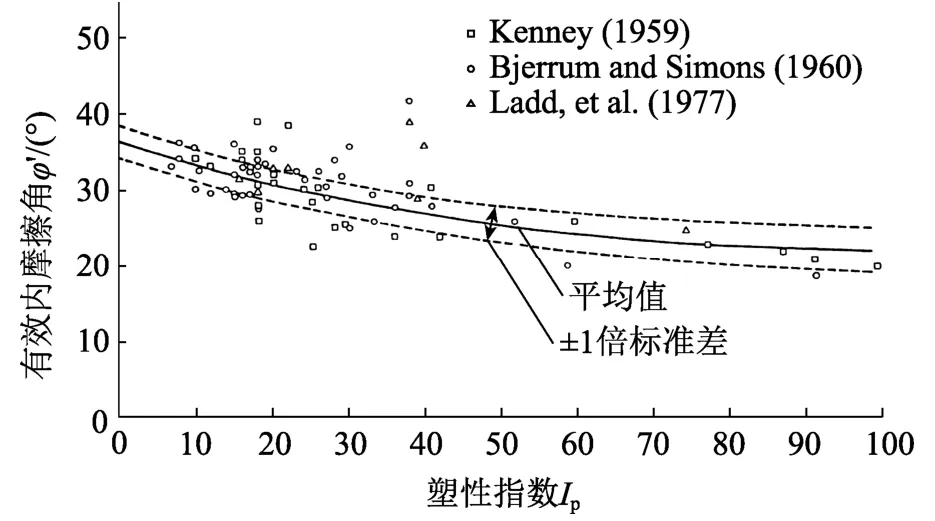
图3 有效内摩擦角与塑性指数经验关系Fig.3 Empirical correlation between φ' and Ip

1.3 考虑固结应力作用的不排水强度指标方法(Method B)

当可以获得固结地基的不排水强度指标时(通过实验室试验、现场试验或其他估算方法获得)，可以采用Method B。该方法不关注真实的有效应力路径，而仅关心不排水有效应力路径与有效应力破坏包线的交点位置。如图1中OB线所示，B点的不排水抗剪强度应指定为通过试验或估算获得的不排水强度指标值，即一般这种方法得到的su是固结应力或地基埋深的线性函数，是符合有效应力原理的。与Method A相同，其默认的破坏面与最大主压应力方向成45°角。

对于显著剪缩的软粘土，或剪胀性土，其有效应力路径不沿垂直向上发展，此时采用Method A就会高估或低估地基土体的强度。引言中提到的Nicoll Highway地铁站就是由于采用了Method A，高估了软土不排水抗剪强度，成为导致事故发生的一个重要原因。但Method B给出的su通常还受到超固结水平、应力路径和样品质量(如果是实验室测定的)的影响，也容易出现偏差。同时为了正确指定su与固结应力或地基埋深的相关关系，Method B对于试验量的需求也较高。

对于不排水强度指标su的估算，此前研究者曾提出过多种拟合方法，影响较广的包括Mesri法和Ladd提出的SHANSEP方法等[13]。

Mesri法指出不排水强度与固结应力具有比例关系，比例系数大致为0.22左右，表达式为：

SHANSEP方法进一步引入了对超固结比OCR影响的考虑，给出如下关系式：

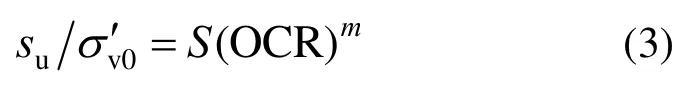
针对不同类型土，S和m系数有不同取值，但其变化范围不大。在无明确指定的情况下，可以取S=0.23，m=0.8作为缺省值。

表1是各方法所需参数和应用条件的总结。

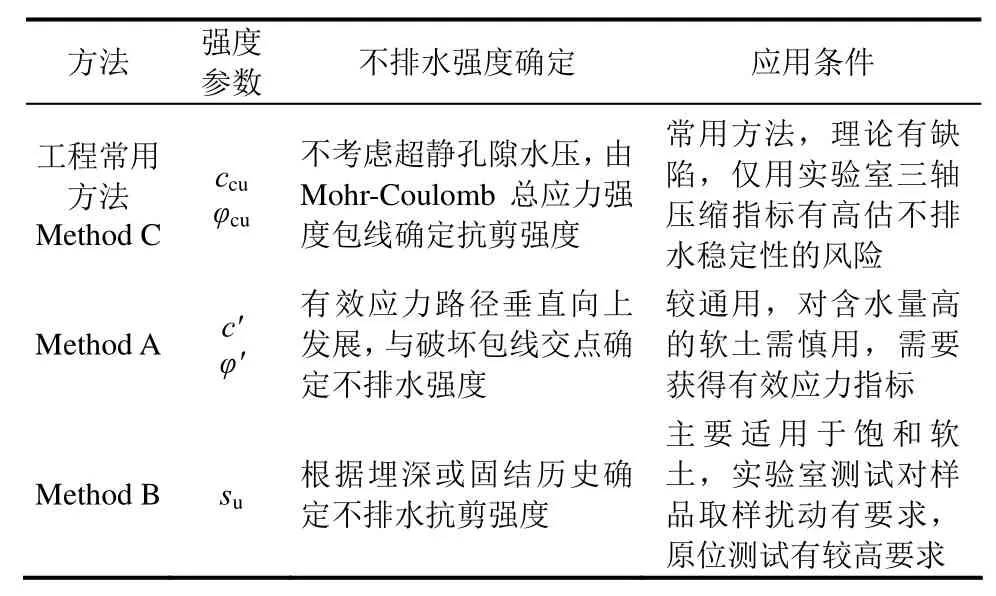
表1 不排水强度与分析方法总结Table 1 Conclusion of undrained strength parameters and analysis methods

2 假想算例分析

针对2个典型边坡算例进行不排水稳定性分析，模型几何形状和尺寸见图4、表2。2个算例选用的饱和地基土体分别为某拟建机场工程区域6粉质粘土和意大利比萨B-2软粘土，土体强度参数见表3。机场粉质粘土的有效应力强度指标和不排水强度指标是分别根据Ip指数和假定OCR值，按照图3、式(3)所述方法进行估算得到的；比萨软粘土强度指标则直接由实验室CD(有效应力指标)、CU(总应力指标)和UU(不排水指标)试验确定[20]。填筑体坡比1∶1，坡高设置随土体强度改变，使其不排水稳定性安全系数约为1.0。通过增加单元网格数和迭代次数，将极限分析上、下限误差控制在5%以内，以下计算只给出安全系数平均值。

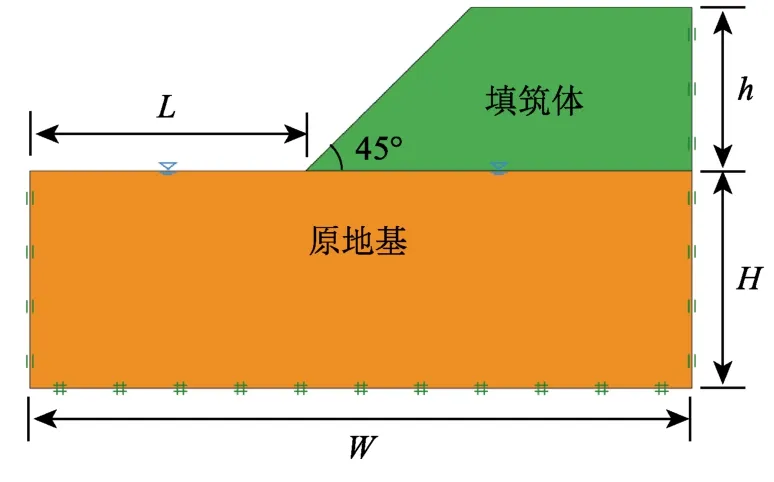
图4 假想模型几何形状Fig.4 Geometry of thought models

表2 假想模型几何尺寸Table 2 Geometric dimensions of thought models

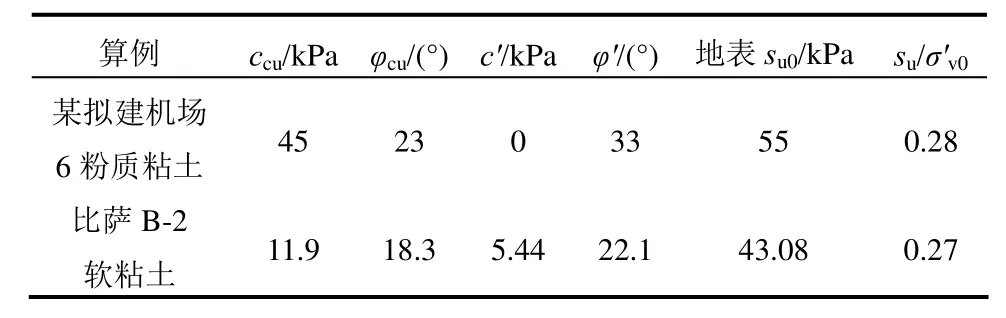
表3 假想模型土体强度参数Table 3 Soil strength parameters of thought models

分别应用工程常用方法(Method C)，以及不排水分析Method A、Method B对两个假想算例模型的不排水稳定性安全系数进行计算。安全系数的定义方法采用强度折减法，为避免填筑体强度对不同方法安全系数计算的影响，设定仅地基土强度可折减，填筑体强度不折减，并且假定填筑体排水条件良好[21]。各方法计算得到的滑移面及其上剪应力见图5(剪应力单位：kPa)，安全系数计算结果见表4。

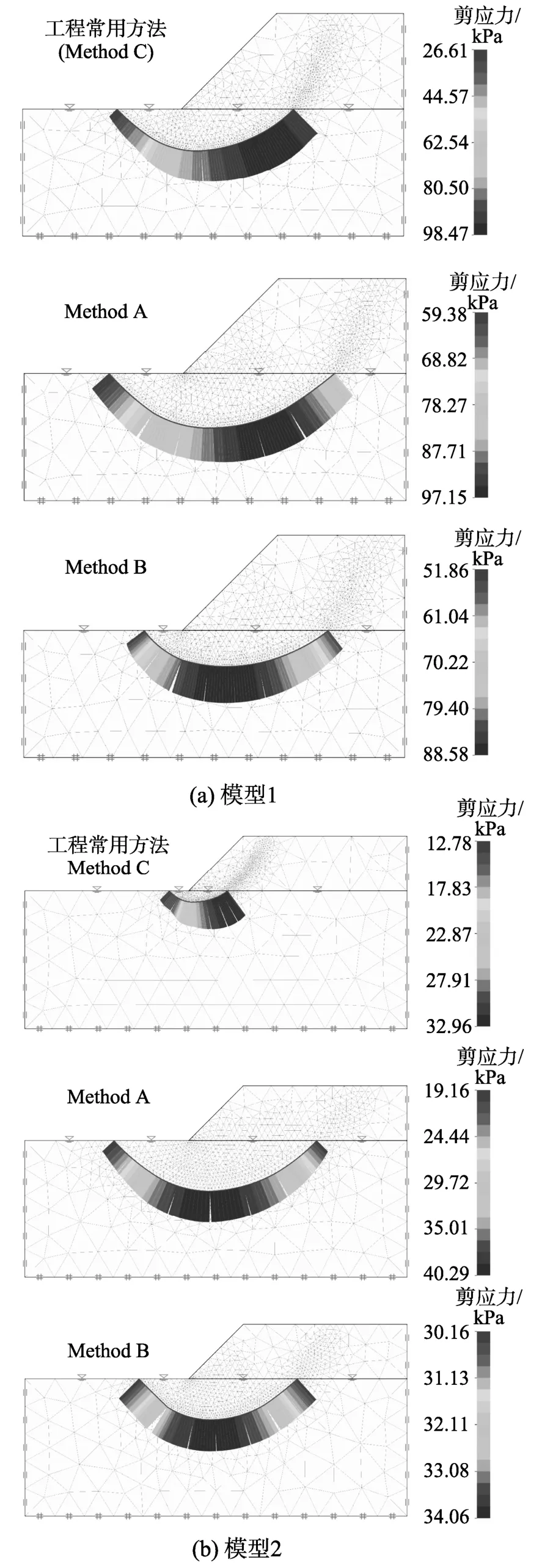
图5 假想模型滑移面及剪应力Fig.5 Failure surfaoes and mobilized shear stress of thought models

对比Method A、Method B与常用工程计算方法，可以看到稳定性安全系数显著降低。对比各方法计算所得滑移面上相同埋深处的剪应力，以模型一为例，在埋深5 m处，Method A、Method B、Method C结果分别为86.4 kPa、70.0 kPa和96.8 kPa，可见由工程常用方法(Method C)计算所得剪应力大于其他两种方法，故而Method C计算得到的安全系数也更高。而对比Method A和Method B，可以看到其剪应力分布有差异：由于Method B所指定的不排水抗剪强度沿深度分布，因此相同埋深处滑移面上的剪应力总相等，呈“左右对称”状分布；而Method A的不排水强度由该点固结应力水平换算得到，因此在填筑体下方的高应力区抗剪强度也更高。这解释了Method A和Method B虽然剪应力分布不同，但安全系数相近的原因。

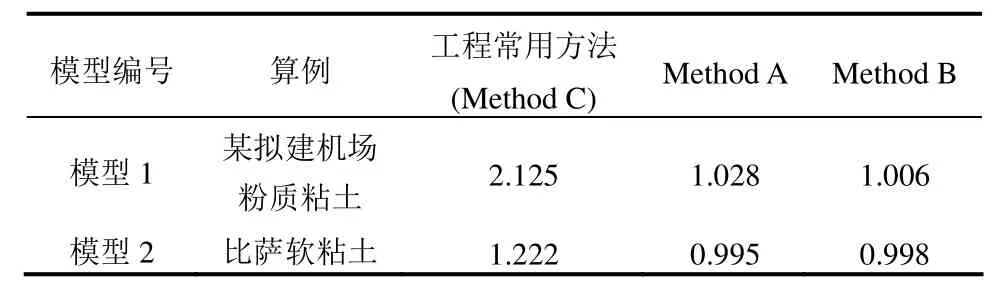
表4 假想模型不排水稳定性安全系数计算结果Table 4 Undrained stability factor of safety of thought models

3 工程设计实例研究

某地近期拟新建一机场，其设计填方高度逾100 m，先行开工试验段填方高度也达到70 m以上，预计施工期为半年。该机场所处位置与引言中所述发生边坡破坏的机场距离仅100余公里，且填方区地下水位埋深较浅处仅1.6 m～10.5 m。为防止该高填方工程边坡发生整体稳定性破坏，有必要关注其不排水稳定性。

边坡典型断面如图6所示，主要土层参数见表5，其中6层粉质粘土即上文算例中所选用的地基土。为验证不排水分析的必要性，首先对该模型进行固结计算。当将全部填筑体土体荷载一次性施加在原地基上时，地基中将产生峰值超静孔隙水压763 kPa。随后，按照施工计划速度将填筑体逐级加载到原地基上，计算施工期结束时的原地表沉降量和超静孔隙水压力。固结计算结果(图7)表明，半年施工期结束时未消散的超静孔压为635 kPa，剩余超静孔压还需9.8年才能完全消散。这说明针对该工程，进行不排水稳定性计算具有十足的必要性。

应用Method A、Method B、Method C计算边坡不排水稳定性安全系数，设计要求其静力稳定性安全系数应不小于1.35。当应用工程常用方法(Method C)时，计算得安全系数为1.241，滑移面主要位于填筑体中(图8)，这意味着原地基抗剪强度高于填筑体，稳定性由填筑体强度控制。因此若想提高其安全系数，可以选用土工格栅加筋方法以增强填筑体稳定性。仅需增加非常稀疏的土工格栅，如图9土工格栅竖向间距10 m，长度50 m，即可将安全系数提升至1.418。此时滑移面发生分叉，其中一支深入原地基中。

但当应用不排水分析方法Method A、Method B进行计算时，其安全系数显著降低至1.0左右，滑移面位置深入至原地基中(图10)。此时进行填筑体加筋(间距1 m，长度50 m)也无显著作用，对于安全系数提高微乎其微，完全无法将其提升至1.35以上(图11)，安全系数计算结果见表6。在滑移面上相同埋深处的剪应力，同样有Method C大于Method A和Method B的关系。

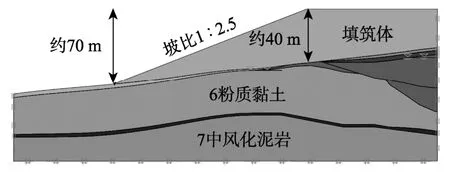
图6 机场高填方典型断面图Fig.6 Typical section of airport high earth-fill

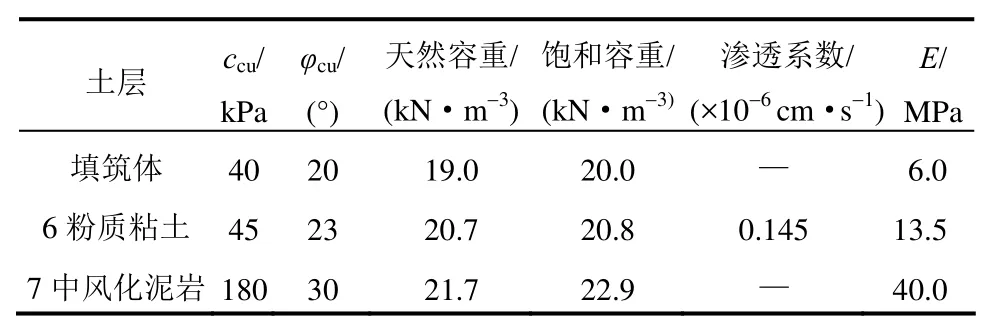
表5 主要土层参数Table 5 Parameters of main soil layers

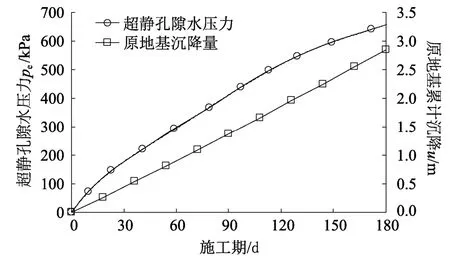
图7 超静孔隙水压和原地基累计沉降随施工期的发展Fig.7 Development of excess pore pressure and accumulative settlement with construction

可以说不排水稳定性分析结果完全颠覆了工程常用方法的结论，对于该工程而言，不排水稳定性起控制作用，且一般边坡加固方法已经不能发挥作用。为了确保该边坡的稳定性，必须从原地基入手，通过地基处理措施，如砂桩、碎石桩或CFG桩，一方面加速超静孔隙水压的消散，另一方面提高地基强度，方能满足工程的稳定性需求。

图8 工程常用方法边坡滑移面及剪应力Fig.8 Failure surface and mobilized shear stress of slope by conventional stability analysis method

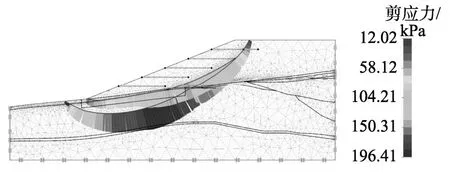
图9 土工格栅加固后滑移面及剪应力(Method C)Fig.9 Failure surface and mobilized shear stress of slope reinforced by geogrid (Method C)

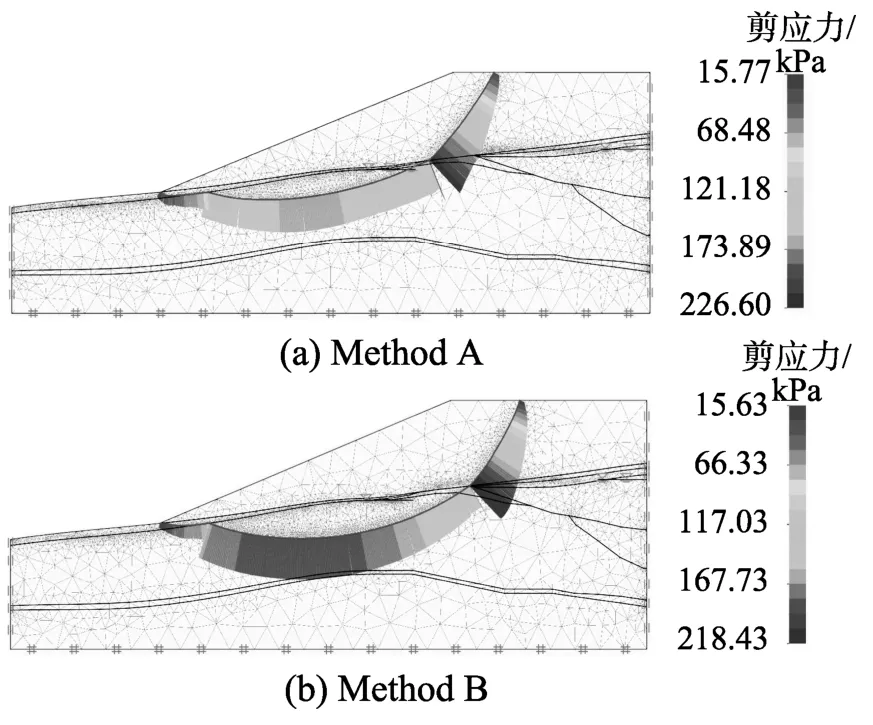
图10 不排水分析边坡滑移面及剪应力Fig.10 Failure surface and mobilized shear stress of slope by undrained stability analysis method

图11 土工格栅加固后滑移面及剪应力(不排水分析方法)Fig.11 Failure surface and mobilized shear stress of slope reinforced by geogrid (undrained stability analysis method)

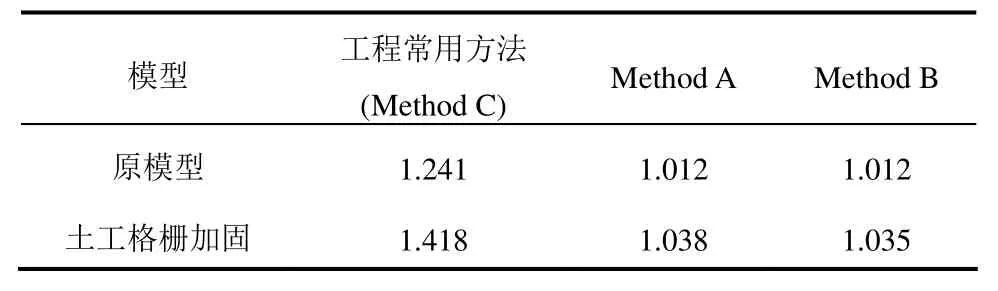
表6 机场边坡不排水稳定性安全系数计算结果Table 6 Undrained stability factor of safety of airport slope

4 结论

本文系统比较了国内外3种不排水稳定性分析方法和相应的强度指标差异，采用有限元极限分析方法，从简单算例入手，到实际工程案例，进行了不排水稳定性计算。主要得出以下结论：

(1) 对于饱和地基上的填方工程建设，当填方高度较大、施工速度较快、原地基排水条件不佳时，需要重点考虑其不排水稳定性。宜先进行固结分析，估计超静孔隙水压的影响程度，从而确定进行不排水稳定性分析的必要性。

(2) 对于不排水稳定性分析，推荐选用有效应力强度指标或不排水强度指标，这两种指标理论完备，符合有效应力原理，能清楚解释不排水问题的力学本质。

(3) Method A和Method B都是不排水分析可行的方法，其中Method A应用最便捷，适用范围较广，对于重要工程，建议进行固结不排水有效应力指标测试，以确定该方法参数；Method B理论上最准确，是针对软土计算必须选用的方法，但其应用时对试验数据需求量较大，有其不便性。

(4) 应用不排水强度的总应力指标(Method C)，由于对地基土不排水抗剪强度各向异性、滑移面上应变协调关系、破坏面方向等因素考虑不足而高估边坡的不排水稳定性。在滑移面上相同埋深处的剪应力，Method C总大于Method A和Method B，其滑移面形状也与后两者不同，是导致Method C计算得到的安全系数高于其他两种方法的主要原因。

鉴于本文当中假想算例模型一和工程案例缺少有效应力指标和基于固结应力的不排水强度指标，因此对以上指标的试验测定和不排水稳定性模拟分析，是下一步研究的重点内容。