马氏瓶回流原理分析1)

姚仰平 陈 伟 陈 含

(北京航空航天大学交通科学与工程学院，北京100083)

马氏瓶是一种能提供恒定水头和恒定流速的装置，它以法国物理学家Edme Mariotte 的名字命名[1]。在试验和生活中被广泛应用，例如作为自动补水装置为水面蒸发仪提供恒定水位，在地下水均衡场的入渗仪中作为计量装置计算入渗量[2]，在实验室经常用于稳定供水和量测[3]。

马氏瓶构造简单实用，但学者们对于马氏瓶工作原理的研究较少，仅有的研究集中在马氏瓶恒定水头补水的基础上[4-5]。对于马氏瓶出水口发生回水的逆过程未有研究，笔者在试验过程中这种情况时有发生。

为了收集覆盖层下锅盖效应生成的水，笔者进行了锅盖效应取水试验，其中锅盖效应是指冬季土中的水气在温度梯度作用下向上迁移，在道面覆盖层下的低温区冷凝或凝华，导致覆盖层下水分聚集的现象[6-13]。试验中利用马氏瓶作为补水装置给土样提供恒定水位。土样经升温后覆盖层下冷凝水和凝华冰融化成液态水流下，使水面高于马氏瓶控制的水位，导致马氏瓶发生了回流，部分融化的液态水回流到了马氏瓶内，造成了损失，为了研究有多少液态水发生了回流，以获知试验中实际生成液态水的量，本文对马氏瓶的回流原理进行了相关研究。

1 马氏瓶恒定水头原理

如图1 所示，马氏瓶与试筒相连，左侧为马氏瓶：图中1○为马氏瓶瓶身。2○为进气管，马氏瓶供水时外界空气从进气管进入瓶内空腔，马氏瓶水量不足时作为注水口给马氏瓶补充水。3○为带有阀门的出气管，马氏瓶正常工作时阀门关闭。阀门打开时有两个作用，一是在给马氏瓶补充水时，打开阀门用来平衡气压出气，二是需要将马氏瓶作为普通连通器使用时打开阀门平衡气压，平衡液面为瓶内液面。4○为出水口，用来给试筒补水。右侧为与马氏瓶出水口相连的试筒，试筒上端开口，筒中的水位可由马氏瓶调节。当试筒中水面低于马氏瓶进气管底端时，进气管底端气体压强小于试筒中水面气体压强，即小于一个大气压，马氏瓶将开始给试筒补水，同时进气管底端逸出气泡上升到水面上部空腔进行补气[14-15]，气体补充的体积即为出水口流出水的体积；随着补水的进行，试筒中水面逐渐上升，当水面上升到与进气管底端平齐时，马氏瓶停止补水，此时进气管底端气体压强为一个大气压[16]，达到平衡状态。在试筒中的水由于蒸发作用而减少时，导致水位低于进气管底端，进气管底端气体压强将再次低于大气压，马氏瓶继续为试筒补水，使水位不断趋近进气管底端直到平齐，达到恒定水头补水的目的。

图1 与试筒相连的马氏瓶

2 马氏瓶回流原理分析

如图2(a)所示，马氏瓶与试筒达到初始平衡状态。若模拟锅盖效应生成水的下落过程，给试筒中添加一定量水使水面高于进气管底端，发现马氏瓶将开始回水，回流的水不仅进入进气管，也将回流到马氏瓶内，如图2(b)所示。其添加的水量Va包括三部分：留在试筒内的水Vb、回流到马氏瓶内的水Vc、进气管中水柱Vd。三者满足关系式

而且发生回流时进气管中水柱始终与试筒中水面同高，因为两者液面直接与大气接触，液面气压相同，且水流之间的通道连通，类似于U型管结构。

图2 引起马氏瓶回流的水量组成

如图3 所示，图3(a)为马氏瓶初始平衡状态，图3(b)为马氏瓶回流后达到稳定状态，由图3(a)中的平衡状态加水回流后实现。p1和p2分别为两种状态下马氏瓶内气体压力，V1和V2为两种状态下的气体体积，由理想气体方程

式中，p为指理想气体的压强，V为理想气体的体积，n为气体物质的量，T为理想气体的热力学温度，R为理想气体常数。无论马氏瓶进气管水柱多高，均没有气体进入马氏瓶，故n恒定，所以上式右端为定值。可知马氏瓶在两种状态下有等式两端同时除以马氏瓶横截面面积，有

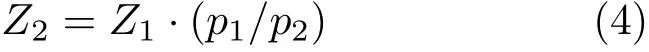
其中

式中，pA为标准大气压；Z1是马氏瓶初始平衡状态时瓶内空腔的高度(cm)；h1为该状态下水面到进气管底端的距离(cm)，可认为是马氏瓶的初始水位；Z2是马氏瓶回流后瓶内空腔的高度(cm)；h2为该状态下进气管中水柱高度(cm)；由于进气管中水柱与试筒中水面同高；也可用h2表示试筒中相对水位；h3为马氏瓶回流后水面到进气管底端的距离(cm)[17]。如图3所示。

图3 两种马氏瓶稳定状态

式(5)～式(6)的等号两端同时除以ρg，用水头表示压力

式中1034 表示为1 个大气压的水头高度，式中高度单位均为cm。将式(7)代入式(4)得到

即马氏瓶中回流水量高度为

可用式(9)计算回流到马氏瓶内的水量。由式(1)可知引起马氏瓶回流所添加的水量为

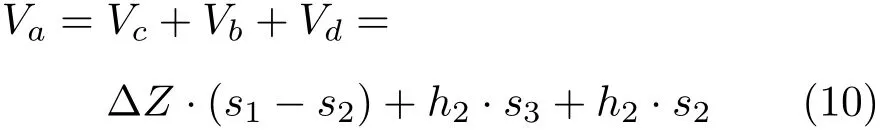
式中，s1为马氏瓶内截面积(cm2)，s2为进气管内截面积(cm2)，s3为试筒内截面积(cm2)，式(10)中忽略了马氏瓶进气管的壁厚，将式(9)代入式(10)中可得

式(11)即为引起马氏瓶回流所添加水量的计算式。从上述推导过程可以看出，马氏瓶发生逆向回流时，马氏瓶内水量增加，水面上部气体压强增大，空腔体积被压缩，压缩的体积由回流的水量补充。由式(9)和式(11)可知马氏瓶回流水量高度与马氏瓶初始水位h1、水面上部空腔高度Z1与试筒中相对水位h2及h3有关，而引起回流所添加的水量除与上述因素有关外，还与马氏瓶、进气管、试筒的截面积有关。

对于同一个马氏瓶和试筒，上式中的自变量为马氏瓶初始水位h1、水面上部空腔高度Z1、试筒相对水位h2和h3，因为h3可由h1，h2和Z1决定(由h3-h1等于式(9)可得)，Z1由h1决定，所以实际的自变量为马氏瓶初始水位h1和试筒相对水位h2。以上参量都可以从马氏瓶上直接获取，可知仅通过观测马氏瓶就可以计算得到引起马氏瓶回流所添加的水量。另外可以发现当马氏瓶初始水位恒定，即h1和Z1不变时，试筒中相对水位h2越高，进气管中水柱越高，h3-h2越小，马氏瓶内回流水量越多，引起回流所添加的水量也越大。

当马氏瓶初始水位h1恒定时，式(11)中的Va只随试筒中相对水位h2变化，两者之间的变化规律如图4所示。

图4 Va 和h2 的变化关系

由图4 可知，Va与h2基本成线性关系，因为Va等于回流的水Vc+Vd与留在试筒中的水Vb之和，且Vb=h2·s3，即Vb与h2成线性关系，因此Vc+Vd与h2基本成线性关系。

因为回流的水Vc+Vd相对Va一般较小，若不考虑回流的水，将Va近似等于留在试筒中的水Vb，用V′a 表示，即

Va与V′a 之间有一个回流水Vc+Vd的误差，两者之间的相对误差用δ表示由上述分析可知：对于同一个马氏瓶和试筒，在马氏瓶初始水位h1恒定时，此时式(11)只有一个自变量h2，且Va与h2基本成线性关系，又有Vc+Vd与h2基本成线性关系，因此上式中的相对误差δ基本为一个稳定值，可认为相对误差δ基本和h2无关。

当马氏瓶中的初始水位h1变化时，相对误差δ也将随之变化，在马氏瓶初始水位h1减小时，回流水Vc+Vd将变大，则相对误差δ将变大；若马氏瓶初始水位h1增大时，回流水Vc+Vd将变小，则相对误差δ将变小。因为回流到瓶内的水是依靠压缩瓶内空腔体积得以进入瓶内，马氏瓶初始水位h1越低，瓶内空腔体积越大，相同压力水头下可压缩气体的量越大，这样就可以留出更多的空间接收回流水，Vc+Vd也将变大，反之亦然。

3 试验分析及验证

为了验证式(11)的适用性及进一步探究马氏瓶回流原理，本文设计了两组马氏瓶逆向回流试验，采用图3 中的试验装置，通过改变马氏瓶初始水位h1、给试筒添加水改变试筒中相对水位h2，探究马氏瓶中回流水量变化。两组试验均采用同一个马氏瓶和试筒，即s1，s2和s3不变，试验中s1=63.6 cm2，s2= 0.28 cm2，s3= 706.8 cm2。因为在试验过程中试筒中相对水位始终高于或等于马氏瓶进气管底端，将进气管底端水平高度处的水位取为0。第一组试验初始条件为Z1=16.5 cm，h1=6 cm；第二组试验初始条件为Z1=6.5 cm，h1=16 cm。两组试验的试验结果和计算结果如表1和表2所示。

表1 第一组试验结果及计算结果

表2 第二组试验结果及计算结果

表中马氏瓶内回流的水量Vc可由式(9)计算，添加水计算值由式(11)计算。由图5 对比试验得到的引起回流实际添加水和计算添加水，可知两者保持一致，说明公式具有适用性。试验中试筒的水量由观测得到，是主要的误差来源。

图5 添加水的实际值与计算值对比

引起回流添加的水主要为试筒中的水，回流到马氏瓶内和进气管中的水很少，但依然不能忽略，且补充的水量越大，总的回流的水越多。由第一组(或第二组)试验可知，当马氏瓶初始水位一定时，给试筒添加的水量越多，试筒中水位越高，回流到马氏瓶内和进气管中的水量越大。

在第一组试验中，观察不同添加水量下Vc+Vd与Va的值，可知总的回流水Vc+Vd占比总添加水Va的比值基本为一个稳定值，为0.18%左右。在第二组试验中，Vc+Vd与Va的比值基本为0.10%左右，比值变小的主要原因是回流到马氏瓶内的水变小了。对比第一组和第二组试验可知，当添加水量一定时，马氏瓶初始水位越低，回流到马氏瓶内的水量越大，而回流到进气管中的水基本不变，进而导致Vc+Vd与Va的比值越大。

对于不同的马氏瓶，s1，s2和s3不同，其最终结果也不一样，如果s1比较大，即马氏瓶截面积较大时，回流到马氏瓶内的水的占比将更大，Vc+Vd与Va的比值也将更大。若s3较大，即试筒截面积较大时，回流到马氏瓶内的水的占比将更小，Vc+Vd与Va的比值也将更小。

由上述分析可知，采用马氏瓶控制恒定水头只能正向补水，一旦试筒中的水由于外界干扰高过马氏瓶进气管底端，就会造成回流，将无法提供恒定水头，进而导致马氏瓶失灵，若仍需用马氏瓶也可以，可用文中公式求得马氏瓶回流水量，以及引起马氏瓶回流所添加的水量。

4 结论

笔者在进行锅盖效应取水试验时发现融化产生的液态水引起了马氏瓶回流，落下的液态水有少量进入了马氏瓶，为了获知试验中实际生成液态水的量，本文对马氏瓶的回流原理进行了相关研究，得出如下结论。

(1)马氏瓶和试筒达到初始平衡状态后，给试筒添加一定量水引起马氏瓶回流，所添加的水量包括三部分：留在试筒内的水、回流到马氏瓶内的水、进气管中的水。

(2)通过马氏瓶的两种平衡状态推导出引起马氏瓶回流所添加水量的计算式，可知，仅通过观测马氏瓶就可以计算得到引起马氏瓶回流所添加的水量。对马氏瓶展开回流试验，将试验结果和计算结果对比，发现实际值与计算值保持一致。

(3)马氏瓶发生逆向回流时，回流的水不仅进入马氏瓶进气管，也会进入马氏瓶内，回流到瓶内的水将压缩水面上部的空气，使瓶内空腔体积减小，气体压强增大。在回流过程中，进气管中的水柱始终与试筒中的水面同高。当添加水量一定时，马氏瓶的初始水位越低，回流到马氏瓶内的水量将越大。