浮体平衡稳定性的研究和应用

岳曾元

(德国体育大学(科隆)，科隆)

浮体，指任何能在静止水面上飘浮的物体。船体是特殊的浮体。其特殊之处在于，船体的外表面是一个开口向上的壳体。开口边界即船沿。这为船体允许的倾斜程度提供了一个上限：船体不允许倾斜到使水漫过船沿。否则船体会倾覆以致沉没。这也为船体及其载荷能承受的外部扰动力矩提供了一个上限。显然，这个上限越高，船体及其载荷越能承受更大的风浪，因而稳定性能越强。

本文首先研究简单的浮体和船体模型的稳定性，并分析和计算简单的船体模型能承受的最大外部扰动力矩；然后将这些分析和计算方法推广到实际船体；最后，将详细比较关于浮体平衡稳定性的6种判据，指出它们各自的优点和局限性，以及相互关系。

1 浮体平衡态的稳定性定义

假定浮体在一定位置和方位下达到平衡。考虑浮体的方位发生了小扰动。则浮体的重心C 会相应地调整其深度，使排水量不变，从而浮力仍等于重力。若作用在扰动态重心的重力与作用在扰动态浮心的浮力产生恢复力矩，则稳定；否则不稳定。

此外，对于船体而言，不但关心当船体从平衡姿态发生微小扰动时能否稳定，而且关心为使船体的倾斜保持在允许范围内，船体能承受的最大外部扰动力矩。后者是代表船体稳定性能的重要指标。

已有多篇文章[1-3]指出过对于浮体稳定性容易产生的一个误解，认为若平衡态下重心低于浮心则稳定，若重心高于浮心则不稳定。第5节将证明，前面一句话是对的，而后面一句话不对，因为重心高于浮心时未必不稳定。这一点可从后面将讲到的许多例子中看出。

2 半球体的平衡与稳定

设半球体的半径为R，重量为W。先设半球体密度均匀，与水密度ρ 之比η ＜1。设平衡时，半球嵌入水中的深度(即半球底部到水面的距离)为H，嵌入体积为

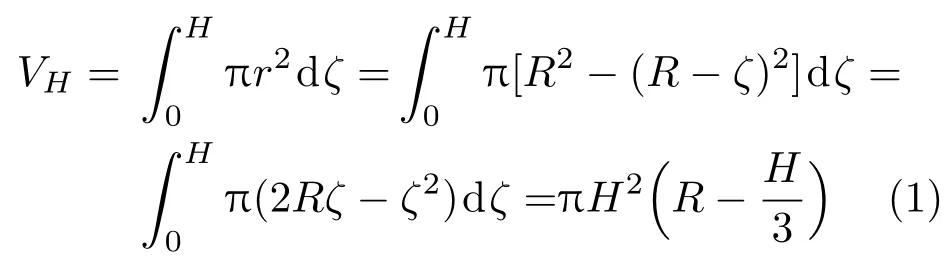
其中r 为嵌入体积中水平圆截面的半径，ζ 为该截面到半球底部的距离(参见图1(a)，其中设η =0.5)。

平衡时浮力与半球体重力相等

得到

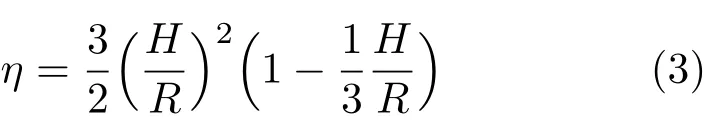
求其反函数需解一个3次方程(标准解法见文献[4])，结果为

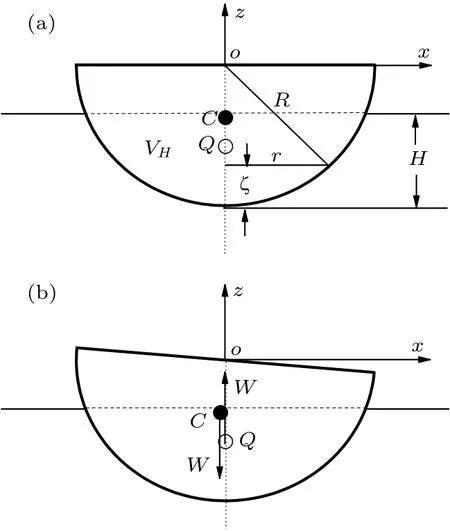
图1

重心C 到半球底部的距离为

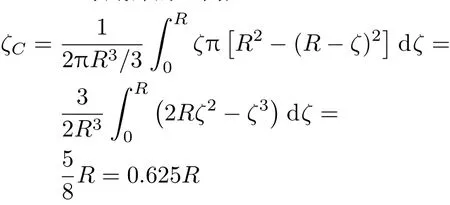
因此半球顶部平面高于重心C 的距离为

排水体积的形心(即浮心) Q 在平衡时到底部的距离为

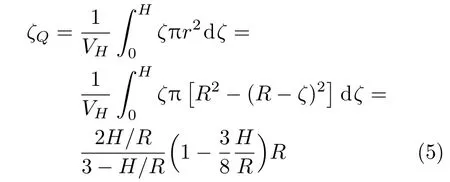
当η =0.5，有

注意，在此例中, 明显有ζC＞ζQ，即重心高于浮心。但此平衡态对小扰动却是稳定的，因为当发生向右的小的倾斜时，对此半球体而言，浮心仍保持在过球心的铅直线上，而重心却向左移动(参见图1(b)，其中倾角θ = 5°)，因而重心与浮心的力偶矩为恢复力矩。只要倾角θ 不超过即只要半球顶部平面的最低点未低于水平面，由重力和浮力产生的恢复力矩为

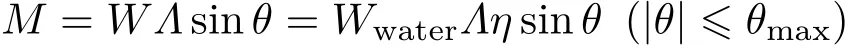
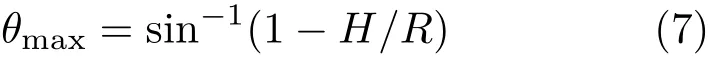
其中Wwater是假定半球充满水时的重量。对于非均匀半球体，只要质量分布关于半球的几何对称轴是轴对称的，并将η理解为该半球实际重量W与Wwater之比，即

则上述所有推导全部成立。唯一不同的是，O点高于重心C的距离Λ将随半球中质量的具体分布而变化。

3 简单船体模型加载的稳定性问题

3.1 均匀半球壳形船体加载的稳定性

设船体为均匀半球壳形，半径为R，船上加载的重物被固定在船体上，且加载物重心在对称轴上，于是总重量W的重心C仍在对称轴上。η仍由式(8)定义。设船口平面高出重心C的距离为Λ。这事实上是上节末尾讨论的非均匀半球体的特殊情形。上节中得到的式(1)～式(6)在这里完全适用，因为它们与Λ无关。对于半球壳船体而言，由式(7)定义的最大偏角θmax有一个更具体的含义：若船体倾斜超过θmax，水将漫过船沿，使船体倾覆乃致沉没。θ=θmax代表半球壳的船沿接触水表面的情形。θ=θmax时的恢复力偶矩为半球壳船体所能承受的最大外部扰动力矩

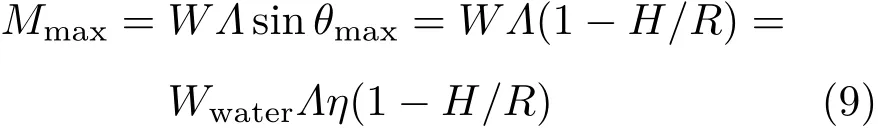
引进无量纲的最大承受力矩

利用式(3)～式(4)，可将μmax/λ只用H/R或只用η表示

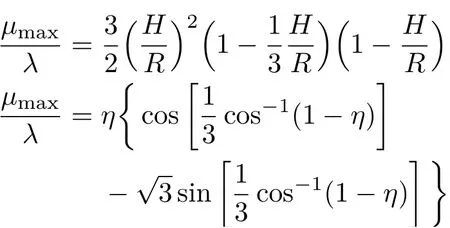
如图2(a)和图2(b)所示。

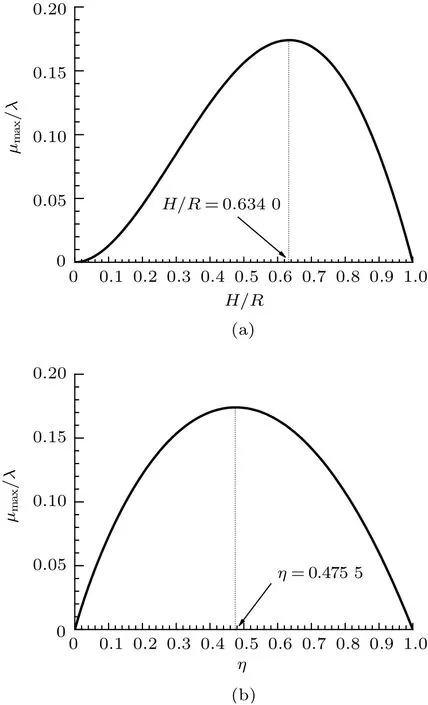
图2

图2 表明，中等吃水深度，或中等载荷的船最有利于承受更大的风浪。这个结论将在下面的讨论中一再被证实。由式(9)可知，重心越低(Λ越大)，则体系越能承受更大的外部扰动力矩，即体系的稳定性能越好。

3.2 均匀半圆柱壳形船体加载的稳定性

设船体为一均匀圆柱壳的一半(横截面为半圆，船沿为矩形)。圆柱半径为R，纵向(母线)长度为L，且L≫R。为简单起见，只考虑关于横向扰动的稳定性问题。取固定于船体的“随体”直角坐标系(O;X,Y,Z)，使得当船体的船口平面处于水平时，原点O位于船口平面中心，Y轴沿纵向，Z轴铅直向上，X轴则指向横向。假定船体与载荷的总重量W的分布关于中心横截面(Y= 0)和中心纵截面(X= 0) 都是对称的。于是，第一，船口平面处于水平的平衡态是存在的，在该平衡态之下，重心C和浮心Q都在铅直线X=Y= 0 上；第二，在横向扰动中，重心C和浮心Q将始终保持在中心横截面(Y= 0)内。由于稳定性及最大允许外力矩的讨论只涉及重心C和浮心Q的位置，因此只需讨论中心横截面(Y= 0)中的二维图像，见图3。图3(a)和图3(b)分别为平衡态和最大允许倾角的状态。设在平衡时，船体在中心横截面的二维“随体”坐标系(O;X,Z)与二维空间坐标系(o;x,z)重合。当船体发生横向扰动时，OZ轴将偏离oz轴, 在zox平面内偏转。

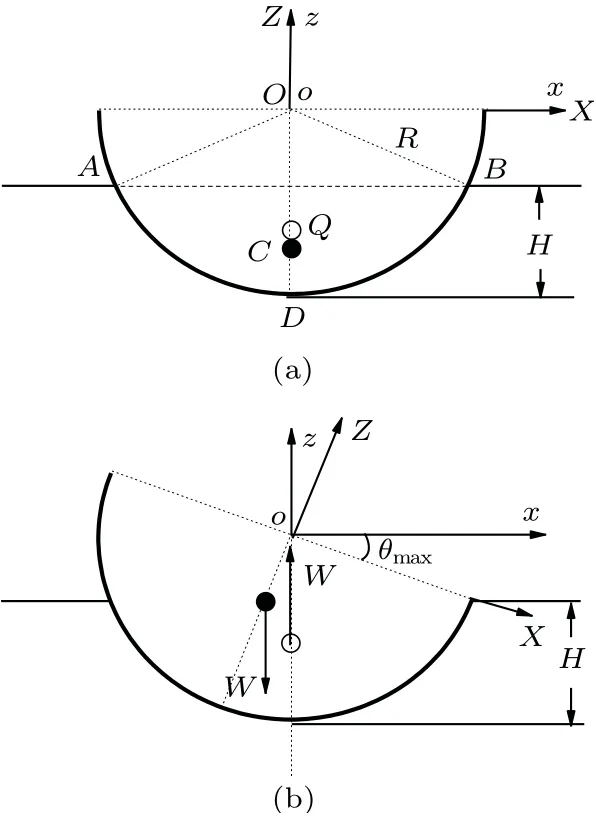
图3

图3(a)中重心C的位置假定是已知的。将总重量W与假定半圆柱壳中充满水的重量Wwater之比定义为η，将平衡时半圆横截面中位于吃水线以下的面积记为SH。由于SH等于图3(a)中oA与oB间的扇形面积减去三角形oAB的面积，容易得到

平衡时浮力与重力的平衡导致

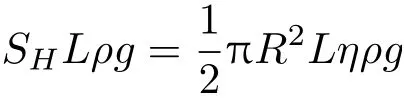
因此得到

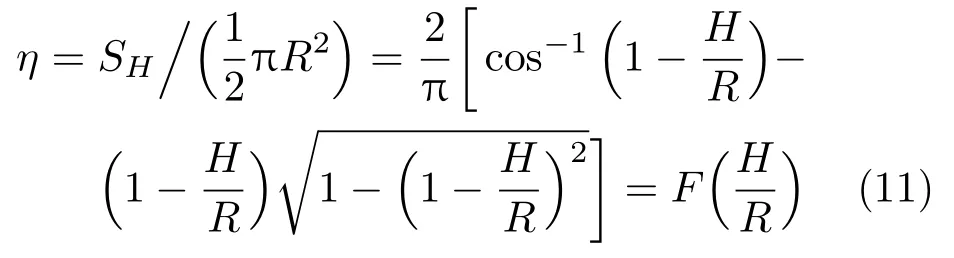
设浮心Q到船体底部的距离为ζQ。有

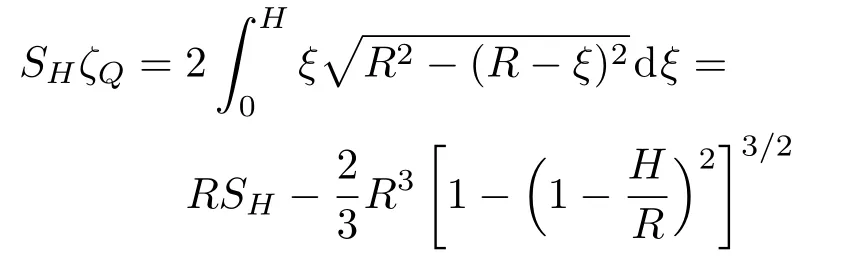
因此得到

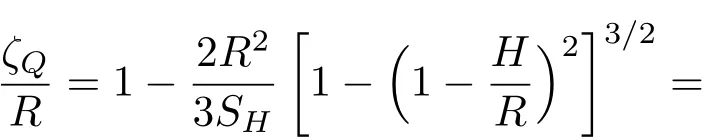
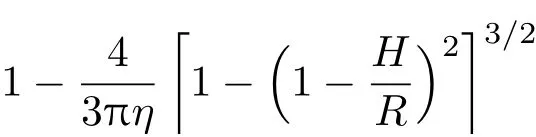
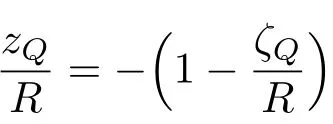
对于η=0.5, 得到

船体在η= 0.5 且处于最大倾角时的横截面如图3(b)所示。重心到船口平面的距离Λ与如何安放货物有关。(该图中Λ= 0.75R是额外假定的) 关于船体能承受的最大侧向外力矩Mmax及其无量纲表示μmax, 式(9)～式(10)仍然成立。只是η与H/R的关系，现在要采用式(11)。于是由式(10)得到

如图4(a)和图4(b)所示。

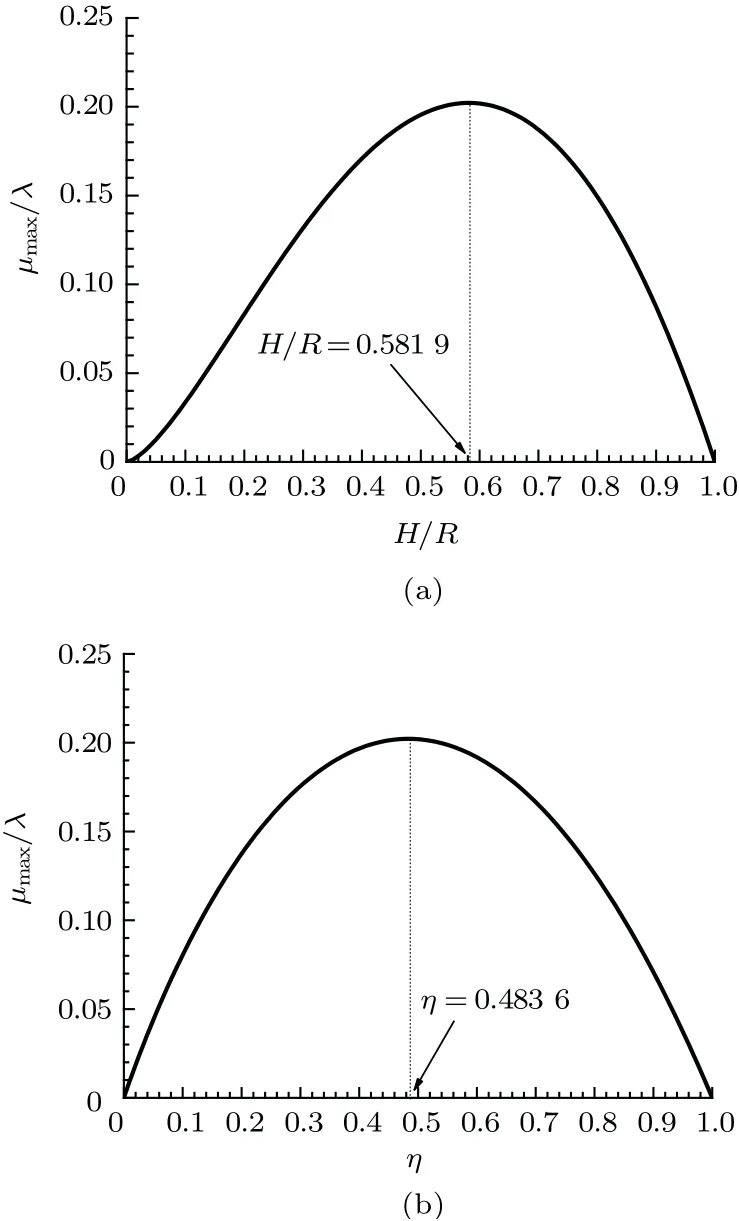
图4

在给定λ(重心位置)情况下，μmax在H/R=0.581 9 或η= 0.483 6 达极大值。再次看到，中等浸水深度或中等载荷对于船体承受外界扰动是最有利的。

3.3 矩形截面柱壳船体加载的稳定性

考虑横截面是宽为b高为h的矩形的柱壳形船体，其纵向长度为L，L≫b。为简单起见，仍然只考虑关于横向扰动的稳定性问题。与3.2 节类似，假定船体与载荷的总重量W关于中心横截面和中心纵截面的分布都是对称的。于是，重心便固定在中心横截面的对称轴上。基于与3.2 节同样的道理，只需考虑中心横截面上的二维图像，如图5 所示。设平衡时，船口平面高于重心的距离为Λ。总重量W与假定矩形截面柱壳中充满水的重量Wwater之比定义为η

其中ρ为水密度,Wwater是假如船容积中充满水时水的重量。设平衡时水平面到船底平面的距离为H，则浮力(bHLρg)与重力(W=bhLρgη)相等导致

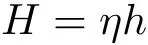
空间坐标系(o;x,z)和二维随体坐标系(O;X,Z)，使原点o位于平衡时吃水平面的中心，x轴向右，z轴向上。在平衡状态下，(O;X,Z)与(o;x,z)重合。平衡时，浮心位置为

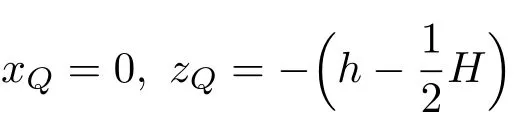
当船体发生较小的横向倾角θ时，浮心Q将偏离过O点的铅垂线(见图5(a))。

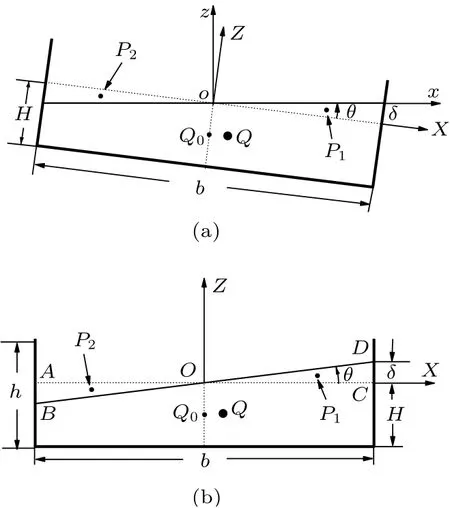
图5

图5(a)给出船体顺时针倾斜θ角时横截面的真实图像：水面是水平的。为使浮力仍等于重力，浸入水的梯形面积必须等于θ= 0 时的浸入水的矩形面积，即Hb。这也意味着水面必通过原点o。为求该扰动态的浮心Q，先考虑浮体坐标系(O;X,Z)中的图像(图5(b))。这里，水面成为向左倾斜的平面BD，与平衡(θ=0, 水面为AC)相比，浸水体积增加了一部分(由三角形OCD所示)，同时减小了一部分(由三角形OAB所示)。这两个三角形的形心分别记为P1和P2。将每个三角形面积与浸水面积之比记为α，有

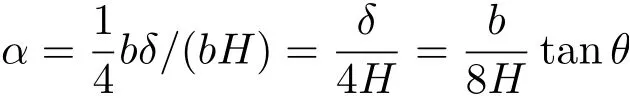
将平衡态时的浮心刻在浮体上，记为Q0, 令它随浮体一起动。则在浮体坐标系(O;X,Z)中有

注意到

得到

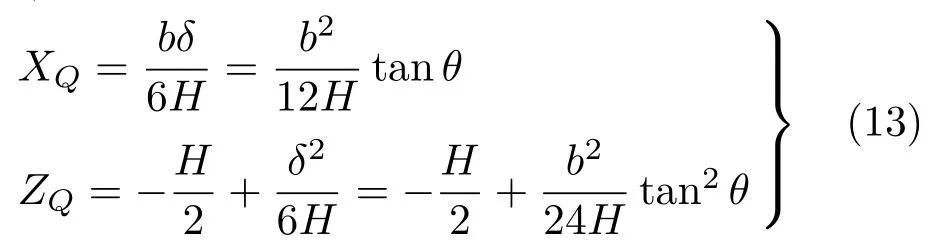
在θ→0 过程中，δ和α都是与θ同阶的小量。由式(12)之第一式可知，的x分量和z分量分别为θ的1阶小量和2阶(或高阶)小量。因此，可将式(13)写成更一般的形式

式(14)适用于任何形状的浮体。重心C在(O;X,Z)系中的坐标为

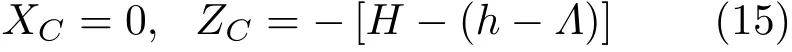
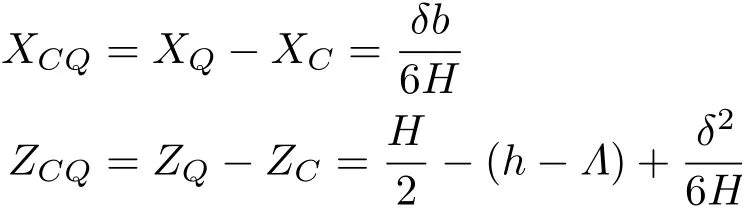
通过坐标变换

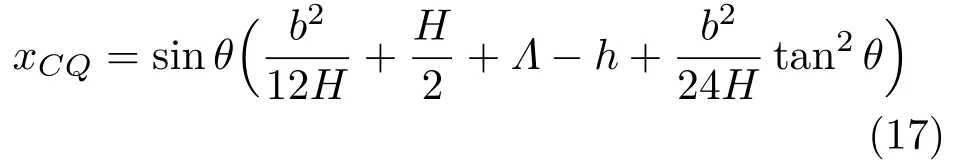
式中Λ为平衡时船口平面高于重心的距离(若Λ ＜0，则表示重心比船口平面高出|Λ|)。重力和浮力产生的恢复力偶矩为

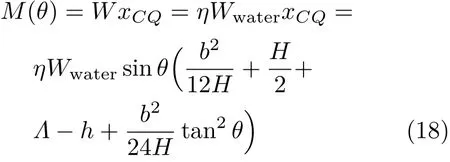
若M(θ)＜0，则表示重力和浮力产生的力偶矩会使倾斜变得更严重，即失稳。引入无量纲恢复力偶矩

则得到

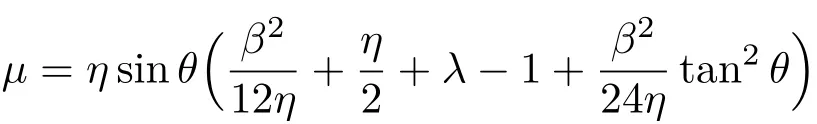
其中

由图5 可知，船体最大允许倾角为船沿接触水面的情形，即

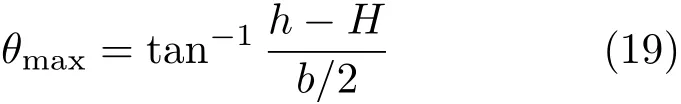
M(θ)在0 ≤θ≤θmax中的最大值就是该船体在给定几何尺寸(h,b,L)和给定总重量及其安排(W,η,Λ)之下所能承受的最大外部干扰力矩。图5中还显示另一个临界倾角，即船底部左端点与水面接触的倾角

倘若η≥1/2，则有H≥h/2, 从而θcrit≥θmax。也就是说，在整个倾角允许范围0 ≤θ≤θmax内，不会遇到水面越过船底部左端点(即θ ＞θcrit)的情形。但倘若η ＜1/2，则有H ＜h/2, 从而θcrit＜θmax。于是在θ达到θmax之前，会遇到θ ＞θcrit的情形。这时浮心Q的计算方法如图6 所示。由于倾斜后浮力大小仍必须等于重力，三角形AEF的面积必须等于Hb，即图6(b)中

由此得出

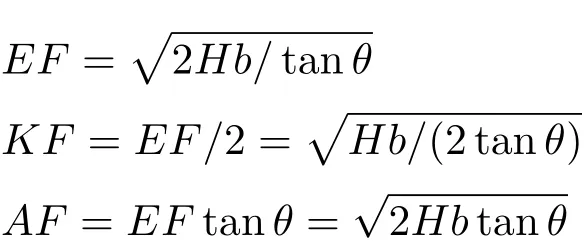
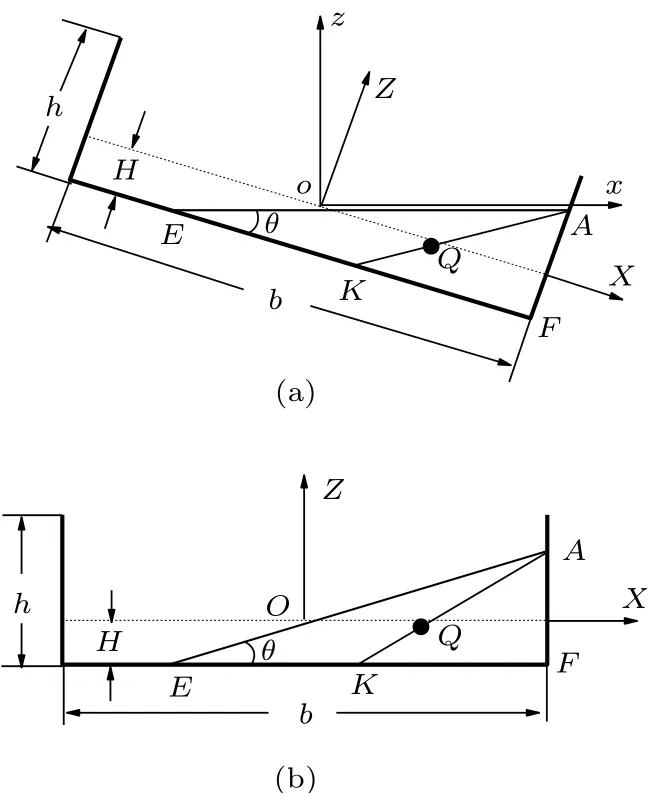
图6

其中K为EF的中点。由此得出A点,K点以及浮心Q点在(O;X,Z)系中的坐标

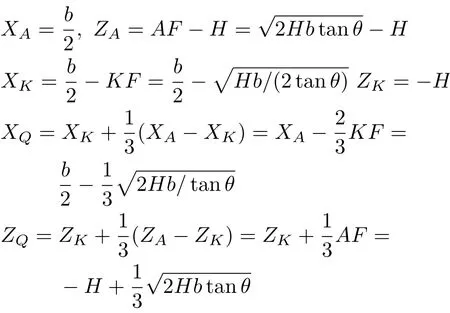
重心C在(O;X,Z)系中的坐标仍由式(15)给出。因此，向量在(O;X,Z)系中的坐标为

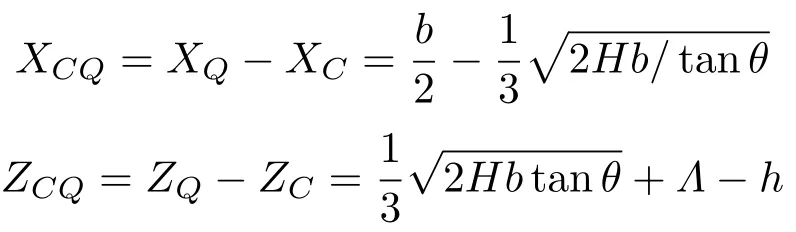
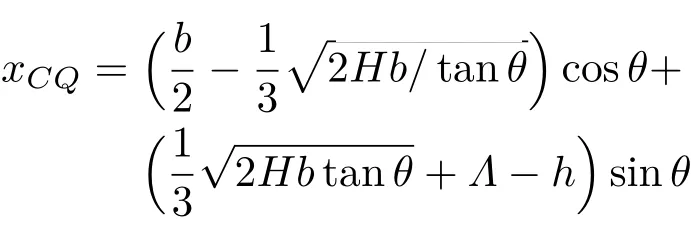
重力和浮力产生的恢复力偶矩及无量纲恢复力偶矩为

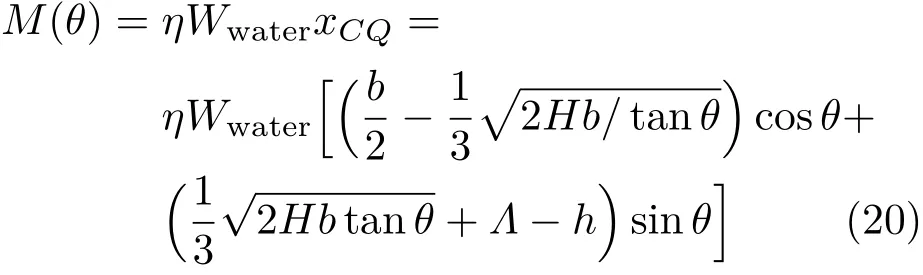
和

至此，已完成矩形截面柱壳船体在给定几何尺寸(h,b,L)和给定总重量及其安排(W,η,Λ)之下恢复力偶矩作为倾角函数的全部计算。下面对稳定条件作一个一般的讨论。在平衡(θ= 0)时，浮心在过重心的铅垂线上。因而

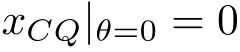
稳定性意味着当发生小的倾角θ ＞0 时，xCQ＞0，从而浮力与重力产生恢复力偶矩。因此，矩形截面柱壳船体加载稳定的充分必要条件是(见式(17))

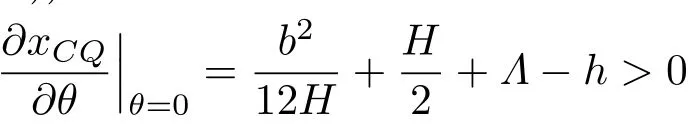
亦即

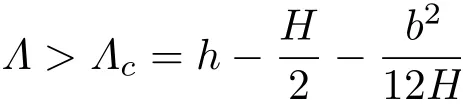
或其无量纲形式

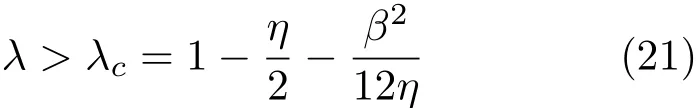
注意η的范围只是0 ≤η≤1。由式(21)可知，对于较宽的船体(例如β=4)，即使重心明显高于船口平面(λ ＜0)，该平衡仍可能是稳定的。

现在来讨论矩形截面柱壳船体在给定几何尺寸和重心位置(h,b,L,Λ)之下所能承受的最大外界扰动力矩Mmax对η(或对吃水深度H=ηh)的依赖关系。Mmax定义为在θ= 0 为稳定平衡前提下恢复力矩M(θ)在0 ≤θ≤θmax中的最大值，其中M(θ) 由式(18) (当η≥1/2)或式(18)及式(20) (当η ＜1/2)给出。最大允许倾角θmax则由式(19)给出，它也可写成无量纲形式

作为一个例子，图7给出在(β=4,λ=0.75)条件下Mmax对η的依赖关系。Mmax在η= 0.41 达最大。再次发现，对不同形状的船体和浮体，Mmax总是在中等载荷，或中等浸水深度达最大。

综上所述，对矩形截面柱壳船体稳定性的研究得出如下有益的结论：

(1) 对于给定的船体深度h, 适当增大船体宽度b, 不但会增大载货量，而且会大大改善船体的稳定性。

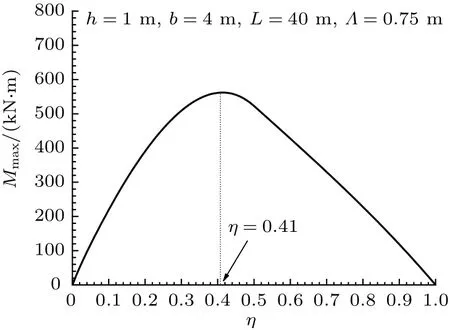
图7

(2) 对于给定的船体与载荷总重量W 而言，重心越低越有利于稳定性。对于较宽的船体，甚至允许重心适当地高于船口平面。这一点对大型的多层游轮和载有多层集装箱的货轮很重要。尽管如此，也应将重心尽可能降低，以获得尽可能大的抗外部扰动能力。

(3) 船体的几何结构决定了它允许的最大浸水深度和最大排水量，因而也决定了它的不可超越的最大总载荷。为使加载船体获得最佳的承受外部干扰力矩的能力，中等载荷或中等浸水深度最有利。

4 实际船体的稳定性

考虑一个任意形状的实际船体，上面有固定的载荷。船体与载荷总重量为W, 它不能超过船体可能的最大排水量的重量，亦即W的上限，Wwater=Wmax，否则水会漫过船沿，造成船体倾覆乃至沉没。仍可定义

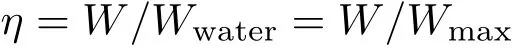
可将船体在平衡时所允许的最高吃水线看成是刻在船体外表面上的几何曲线，而将此几何曲线所在的几何平面定义为“船口平面”，将船口平面到船底(指平衡时过船外表面最低点的水平面)的铅直距离记为h，将船口平面高于总重量W的重心C的距离记为Λ。注意，船口平面,h,Λ三者都是“随体不变量“，即不因船体之倾斜而改变。

仍将总重量为W的船体在水面平衡时，吃水线到船底的铅直距离记为H，将过重心C的铅直线与“吃水平面” (即过吃水线的平面)之交点作为“空间坐标系”的原点o，且令oz轴铅直向上，oy轴水平向前。于是ox轴为水平且指向由船尾向船头看时的右侧。将此坐标系三个轴上的单位向量分别记为eeex，eeey和eeez。平衡时，定义“随体坐标系”(O;X,Y,Z)与空间坐标系(o;x,y,z)重合。设该平衡态时，船体外表面的形状满足方程

引进

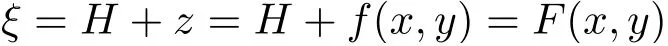
则ξ为平衡时外表面任一点(x,y)到船底平面的高度。当船体发生倾斜时，ξ=F(X,Y)则代表外表面任一点(X,Y)到过“船底点”的切平面的垂直距离。F(X,Y)和f(X,Y)=F(X,Y)-H都是”随体不变量“，即不随船体倾斜而改变。所不同的是，F(X,Y)只依赖于船体外表面的几何形状，而f(X,Y)则还依赖于平衡时的浸水深度，从而依赖于总重量W。对于给定的船体，ξ=F(X,Y)是已知函数。虽未必能用统一的解析式给出，但可从设计图纸或实际测量得到。将总重量为W和Wwater=Wmax时吃水线在xy平面投影所围的区域分别记为DH和Dh，则有

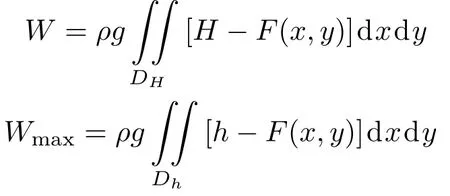
其中ρ为水的密度。于是有

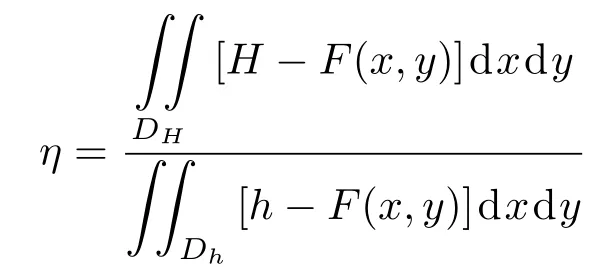
首先讨论当船体只发生横向倾斜，OZ轴相对于oz轴在x方向倾角为θ时，浮心Q的求法。在随体坐标系(O;X,Y,Z)中看，船体外表面仍由方程

给出。而吃水面则为一个向左倾斜的平面

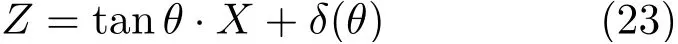
其中δ= 0 (当θ= 0)。倾角为θ时排水体积V仍必须与平衡时的排水体积相同

其中V为斜面(式(23))与外表面(式(22))之间的体积，Dθ为斜面(式(23))与外表面(式(22))之交线在XY平面投影所围区域。由式(24)定出δ之后，浮心Q(即体积V的形心)在随体坐标系(O;X,Y,Z)中的坐标为重心C在随体坐标系(O;X,Y,Z)中的坐标为

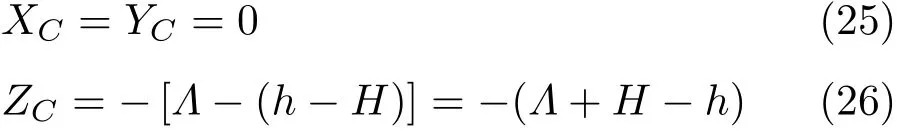
由此得到纯横向倾斜且倾角为θ时浮力与重力的恢复力偶矩为

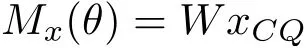
其中θ不超过最大允许横向倾角θmax。船体所能承受的最大横向外界扰动力矩为

纯横向倾斜稳定性判据为

这可由式(27)来判断。可用完全类似的方法讨论纯纵向倾斜，OZ轴相对于oz轴在y方向倾角为φ时浮心Q的求法。在随体坐标系(O;X,Y,Z)中看，吃水面为一个向后倾斜的平面

其中Δ=0 (当φ=0)。排水体积V必须等于平衡时的排水体积，即

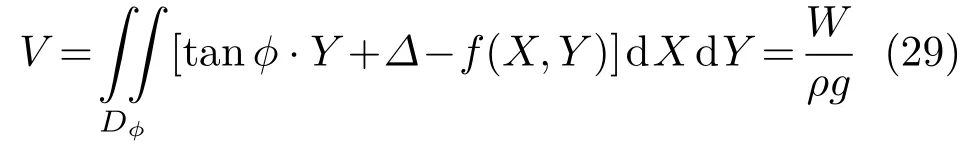
其中V为斜面(式(28))与外表面(式(22))之间的体积，Dφ为斜面(式(28))与外表面(式(22))之交线在XY平面投影所围区域。由式(29)定出Δ之后，浮心Q(即体积V的形心)在随体坐标系(O;X,Y,Z)中的坐标为

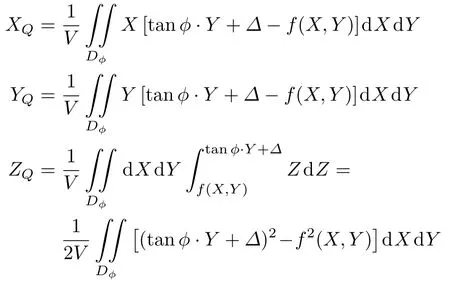
重心C在随体坐标系(O;X,Y,Z)中的坐标仍由方 程(25)和(26)给 出。 向 量--→CQ在 随 体 坐 标 系(O;X,Y,Z)中的坐标为

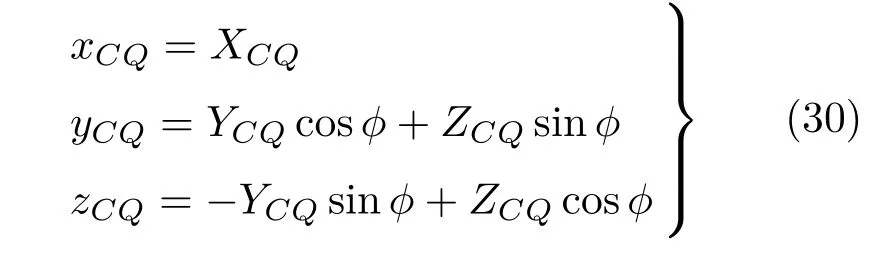
将最大允许纵向倾角记为φmax，于是得到纯纵向倾斜且倾角为φ(φ≤φmax)时浮力与重力的恢复力偶矩为

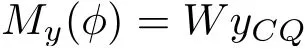
船体所能承受的最大纵向外界扰动力矩为

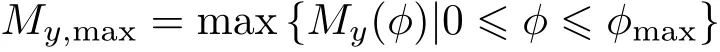
纯纵向倾斜稳定性判据为这可由式(30)来判断。至此，已完成任意形状船体在给定重量和重心时，对横向和纵向倾斜的稳定性及所能承受最大外部扰动力矩的推导。实际船体的设计除了考虑稳定性(包括承受外部扰动力矩的能力)之外，还需考虑货运量，行进速度，建造费用等因素。例如，增大船体宽度固然对货运量和稳定性都有利，但也会增大行进的阻力，从而降低行进速度，并且也会增加建造费用。内河航运的游船和货船还需考虑河水宽度和桥墩间距等因素。

5 讨论

现在将浮体稳定平衡的各种判据作一小结，比较它们各自的优点和局限性，以及它们之间可能存在的逻辑关系。

判据1

定理1浮体平衡时，若重心低于浮心，则该平衡态是稳定的。

证明设水面为z= 0。eeez为z轴单位向量，指向上。平衡时，重心C和浮心Q在同一铅直线上，且已知

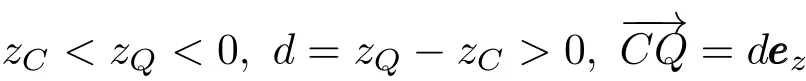
将过C和Q的直线与水面的交点取作原点o。在浮体上取一个平衡时与ez重合的“随体”单位向量EZ。现考虑浮体方位从该平衡态发生一个小偏离达到一个扰动态。无妨设扰动态的EZ与eeez所在的平面为xoz平面，EZ从eeez向x方向倾斜了一个角度θ。将平衡时的浮心刻在浮体上的位置记为Q0，它随浮体一起动。令随体坐标系(O;X,Z)在平衡时与空间坐标系(o;x,z)重合。在扰动态(θ ＞0)仍有

即

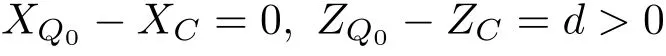
由式(14)，有

将以上二式相加，得到

因此扰动态重力和浮力的力偶矩是恢复力矩。故该平衡态稳定。证毕。

此判据的优点是其简单性：完全不必计算扰动态浮心的位置。此判据的局限性是，它只适宜于浮体重心低于浮心的情形。此情形只有不均匀浮体和船体，当重量集中在底部附近时才会出现。密度小于1的均匀浮体，其平衡态有一部分露出水面，重心一定高于浮心。

判据2

力偶矩法

对于平衡态附近的扰动态，重心位置由随体变化容易得出。只要算出浮心的位置，便可直接判断扰动态重心与浮心力偶矩是不是恢复力矩，从而判断该平衡态是否稳定。此方法的优点是，第一，它普遍适用于一切浮体；第二，它无需计算“浮心曲线”或“浮心曲面”的具体形状；第三，此法便于计算船体所能承受的最大外部扰动力矩，如本文在第3 节和第4节中所作的那样。

判据3

最小总势能法

浮体只受重力和浮力。重力场是有势的，做功与路径无关，因而有重力势能。若将水面定义为z= 0(z ＞0 和z ＜0 分别表示水面以上和水面以下)，并将重力势能的零点取为z= 0, 则浮体的重力势能UG可简单地表示为

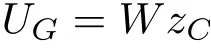
其中W为浮体重量，zC为重心C的z坐标。类似地，可以引进“浮力场”

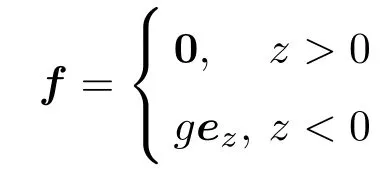
它在z ＜0 和z ＞0 分别为两个有势场，但在z= 0处间断。容易证明“浮力场”f 做功与路径无关，或等价地，“浮力场” f 沿任一闭曲线c做功为零。事实上，若闭曲线c完全在z ＜0 区域或完全在z ＞0 区域，这是显然的。当闭曲线c的一部分在z ＜0 区域而其余部分在z ＞0 区域时，对每段水面以上的部分，可用从该段的出水点到入水点的从下方紧贴于水面的直线段来代替，因为本来浮力场对z ＞0部分做功就为零，而紧贴于水面的直线段上，浮力场与线段垂直，做功亦为零。经过这样替代后的整个闭曲线c′处于z ＜0的有势场中, 因而

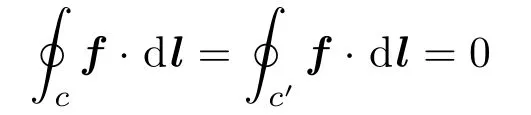
由于当浮体整个处于水面以上时浮力为零，因而浮力在z ＞0不做功，自然将浮体整个处于水面以上的状态定义为浮力势能为零。于是，浮体在任一姿态下的浮力势能UF便是将浮体从该姿态向上提升出水面过程中浮力所作的功，也就是该过程中浮力对浮体浸于水下部分所有体积元做功之和

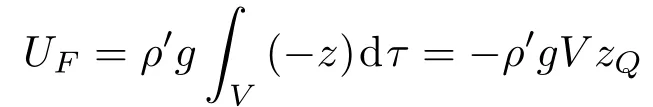
其中V为浮体位于水面以下的那部分体积,ρ′为水密度。此式对浮体的任何位置和姿态都成立。特别，对于浮力等于重力的情形(包括平衡态)，有

因此，在浮力等于重力这一限定下，有

于是，在浮力等于重力这一限定下，可将总势能U简单地写成

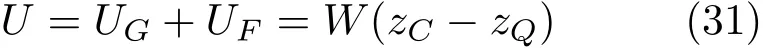
由此得到

定理2浮体平衡态是稳定平衡的充分必要条件是重心与浮心的高度差zC-zQ在浮力等于重力这一限定下达极小。

证明由稳定平衡的最小总势能原理和式(31)立即得证。

(注意，“浮力等于重力”这一限定是必要的。若取消这一限定，例如对均匀浮体，可将浮体整个按入水中，重心将与浮心重合，zC-zQ将等于零。)

推论1浮体的稳定平衡态若重心高于浮心，则重心与浮心的距离在浮力等于重力这一限定下达极小。

证明重心C与浮心Q的距离为

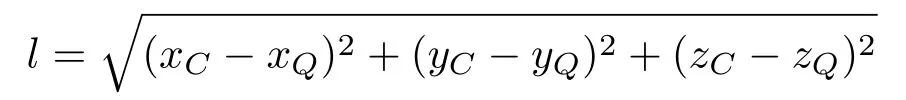
由于该稳定平衡态重心C高于浮心Q，由定理2知，该稳定平衡态的zC-zQ在浮力等于重力这一限定下达极小。在平衡态，重心C与浮心Q在同一铅直线上，上式根号下的前两项为零。因而距离l在浮力等于重力这一限定下达极小。

推论2密度小于1 的均匀浮体的稳定平衡态，其重心与浮心的距离在浮力等于重力这一限定下达极小。

证明密度小于1 的均匀浮体的平衡态，重心一定高于浮心，于是由推论1立即得证。

将上述推论1和推论2总结为

判据4

密度小于1 的均匀浮体的稳定平衡态(或非均匀浮体重心高于浮心时的稳定平衡态)，其重心与浮心的距离在浮力等于重力这一限定下达极小。

稳定平衡时重心与浮心距离达极小这一说法常在一些文章中用到[5-7]。这里则给出了从总势能最小原理推导出这一判据的逻辑关系。

判据5

定倾中心法：

当浮体处于平衡态时，浮力等于重力，重心与浮心处于同一铅直线上。设想将这一铅直线刻在浮体上，称为“刻线”。当浮体偏离该平衡态，保持排水量不变，而倾斜到一个扰动态时，“刻线”将达到一个新位置。而浮心也由扰动态排水体积的形状而达到一个相应的位置。将过扰动态浮心的铅直线与扰动态“刻线”的交点称为“定倾中心”。该判据称，若扰动态的重心低于定倾中心，则稳定；若扰动态的重心高于定倾中心，则不稳定。许多作者讨论过这一方法[1-3,5,8]。对于二维问题，不难看出，此法与力偶矩法等价。但在三维扰动的一般情形下，过扰动态浮心的铅直线是否与“刻线“相交，会引出一些数学上的复杂讨论。总之，虽然在船舶设计中这是一个常用的概念，使用起来，它并不比上述4种判据更方便。

判据6

当浮体具有明显的对称性，使得从直观上即可判断它只有有限的几个平衡姿态时，可直接比较这些平衡态的总势能，或重心浮心的高度差zC-zQ，或(当重心高于浮心时)重心浮心距离l，来直接判断哪些平衡态稳定，哪些平衡态不稳定，而不必对这些平衡态之间的扰动态作任何计算。(见下面的例1)

例1横截面为矩形(长为a, 宽为b,a ＞b)的均匀柱体，密度与水密度之比为η ＜1，能以(1)卧式和(2)立式两个姿态在水面平衡(图8)。

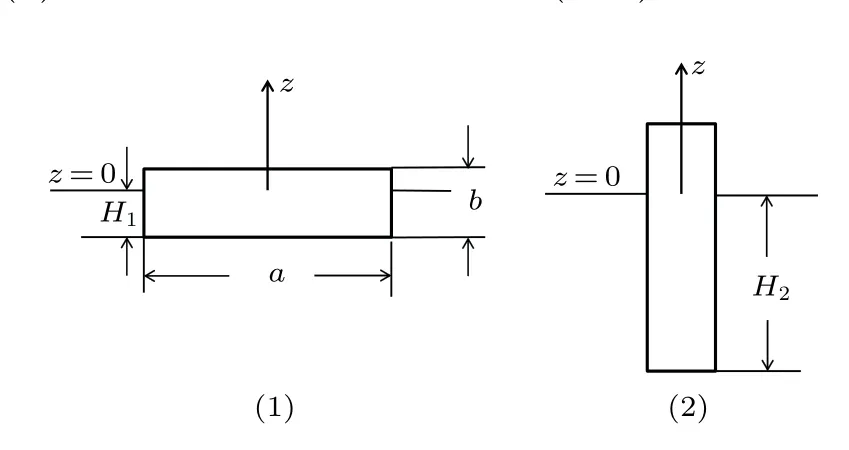
图8

易知在卧式和立式两个姿态下的浸水深度分别为

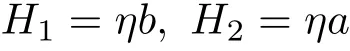
两个姿态下的重心(分别记为C1和C2)和浮心(分别记为Q1和Q2)的z坐标分别为

显然zC1-zQ1＜zC2-zQ2。又由直观判断，zC-zQ不可能在卧式和立式两个姿态之间的任何中间态达极值。因此，zC-zQ必在卧式(1)达极小，在立式(2)达极大。因而，卧式平衡(1)稳定，而立式平衡(2)不稳定。

例2再次考虑3.2 节中讨论过的半圆柱壳形的船体模型。设船体与加载的总重量W小于该半圆柱壳中充满水时水的重量Wwater，则平均密度与水密度之比

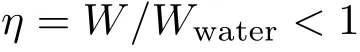
设船体与加载的质量分布沿纵向均匀，且在横截面上关于对称轴对称分布。在此条件下，该加载船体在水面平衡时的浸水深度和浮心位置完全由圆半径R和总重量W决定，与总重量W在铅直方向如何分布无关。因此，可以在保持总重量W不变前提下调解其铅直方向分布，从而相应地调解重心位置，而保持浮心位置不变。

图9 是针对η= 0.5 算出的浸水深度和浮心位置Q。调解质量的铅直方向分布可分别得出平衡时图中所示的重心位置C1,C2,C3。其中，C1在浮心Q之下；C2在浮心Q之上，但在圆心O之下；C3则在圆心O之上。当船体连同载荷向右倾斜角度θ时，只要θ在允许范围内(即水不漫过船沿)，则浮心Q的空间位置不变，而重心C1，C2，C3分别随船体旋转到D1，D2，D3。注意此问题中定倾中心就是O点。对于平衡态C1，可用判据1，2，3，5 中任何一个，断定它是稳定平衡；对于平衡态C2，可用判据2，3，4，5 中任何一个，断定它是稳定平衡；对于平衡态C3，可用判据2，3，4，5 中任何一个，断定它是不稳定平衡。此问题中，可以对平衡态C1,C2和C3直接算出重心与浮心距离作为倾角θ的函数

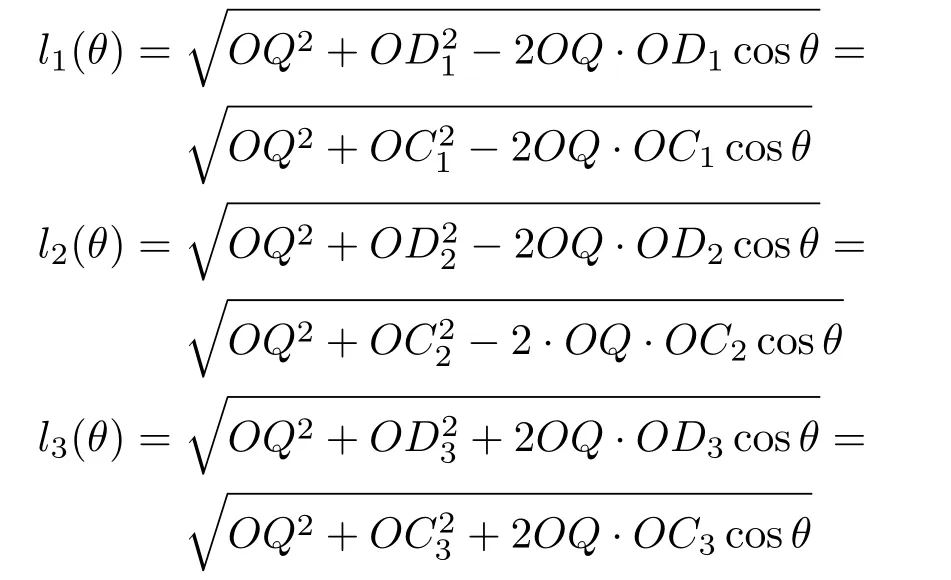
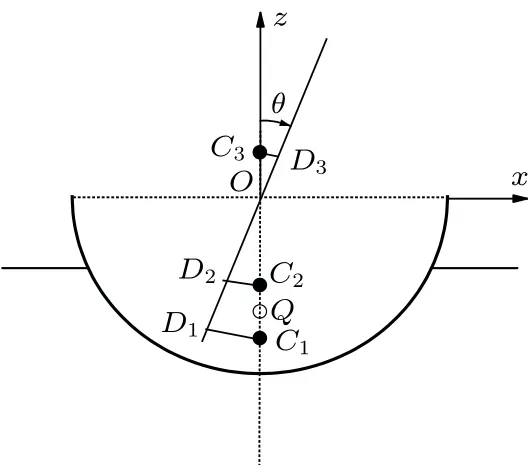
图9

显然，l1(θ)和l2(θ)分别在θ= 0 达极小值QC1和QC2。而l3(θ)则在θ= 0 达极大值QC3。注意，l2(θ)和l3(θ)分别在θ=0 达极小和极大是判据4(或总势能极小原理)的自然推论；而l1(θ)在θ= 0 达极小虽是事实，却不是判据4(或总势能极小原理)的推论。

6 结语

本文通过尽可能简单的模型，讨论了浮体(包括船体)平衡的稳定机制和判据，给出求船体能承受的最大外部扰动力矩的计算方法。这些方法不但适用于简单的船体模型，而且适用于实际的船体。这对改进船体设计会有一定参考价值。本文中对各种稳定性判据的详细讨论有助于澄清该领域的一些基本概念，为改进该领域的教学和研究会有所助益。

致谢作者谨向武际可教授表示衷心的感谢。感谢他建议作者深入考虑了这个有兴趣的课题。并且作者从和他的多次讨论中，获得许多有益的启示。