飞行器角速度测量的三轴加速度计法

刘晏铭 武 迪

(清华大学航天航空学院，北京100084)

角速度测量问题在航天航空、自动驾驶、手机软件等领域有着广泛的应用[1]。现今主流的测量角速度的方法是利用陀螺仪来完成。使用陀螺仪来测量角速度的优点在于测得的值较为准确，且误差较小。但是陀螺仪造价昂贵，工艺复杂，在长期使用之后，其性能和可靠性也会在一定程度上有所降低[2]。鉴于此，人们正在积极发展代替陀螺仪的测量方法。大量文献显示，此前人们将主要研究重心放在了磁流式角速度测量仪[3-4]、光电效应式角速度测量仪上面，并通过滤波方法提高测量精度[5-8]。随着科技的进步，近年来，加速度计的制造相较于陀螺仪而言是非常廉价的，这使得通过三轴加速度计来进行姿态调控成为可能[9]。本文通过理论推导与计算研究，建立了一种通过三个非共线点的加速度测量、计算刚体加速度的算法。这种方法可以极大地降低角速度测量仪的价格。我们利用定轴转动圆柱体上三个非共线点的加速度验证了计算结果的正确性。考虑到飞行器在运行过程中，加速度计测量会有误差，我们对计算结果进行了误差分析和数值模拟，评估了方法的使用范围。结果表明，这种方法在高速稳态飞行器上拥有很好的表现。

1 角速度测量算法

考虑如图1 所示的三个非共线点之间的位置关系。记A1到A3的位矢为r13，A2到A3的位矢为r23。记A1的加速度为a1，A2的加速度为a2，A3的加速度为a3。

根据刚体力学中的计算加速度的基点法可列出

其中ω 为刚体的角速度，ε为刚体角加速度。

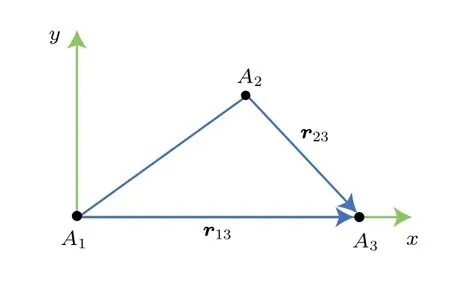
图1 非共线三点位置关系

如果巧妙地选择坐标系，可以使得xy平面与三点所组成的平面共面，故而令x轴为r13所在方向。如图1 所示。在此坐标系下，r13和r23的分量得到极大简化，r13y，r13z和r23z皆为零。方程可化简为

因为所要求的为ωx，ωy，ωz，故而从上面挑选相应的四个方程进行计算，可以解出

式(3)前两式相减可得

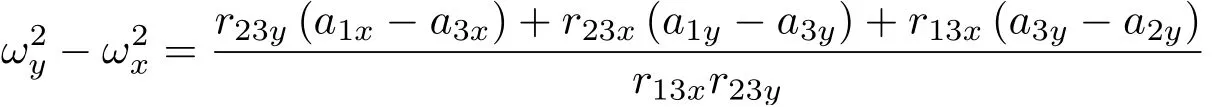
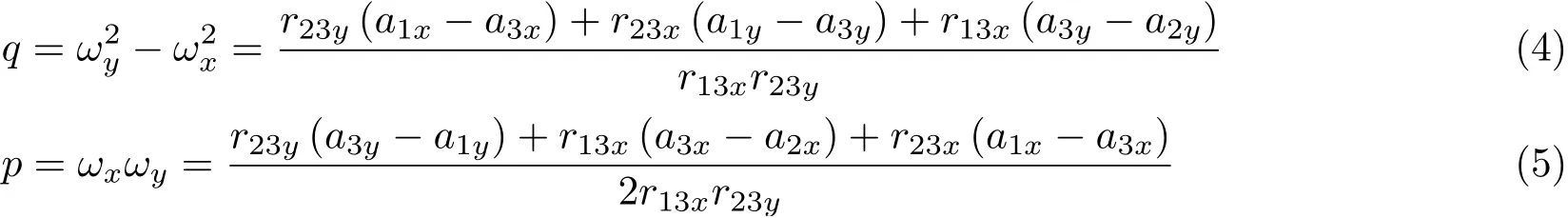
令将式(4)～式(5)化为二次函数的形式，解得

2 角速度误差分析

本文假设每一个方向测量的角速度都满足相互独立的正态分布，且不考虑距离的变化。即aij∼N(μij,σij)。N(μij,σij)代表正态分布，μij为正态分布的期望，σij为正态分布的方差。

根据概率论的知识可知，正态分布具有再生性。正态分布的和差也是正态分布，即为

式中，E(aij-akm)代表两个量差的期望，Var(aij-akm)代表两个量差的方差。

再考虑正态分布乘常数，假设X∼N(μ,σ)，令Y=aX，a为一常数。则根据f(y)= dF

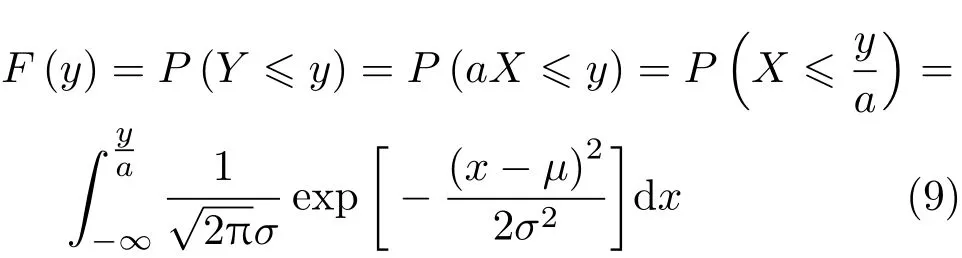
d

(yy)，

利用微积分知识可以算得

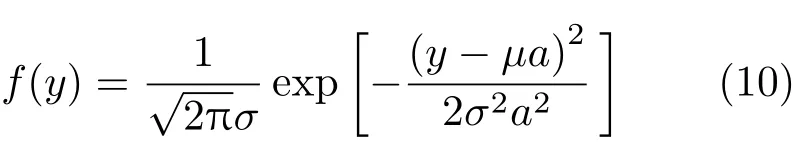
综上可得正态分布乘积的概率分布，依旧是正态分布

再根据概率论的知识，若X1,X2,···,Xn独立，则f1(X1),f2(X2),···,fn(Xn)独立。从而计算得到q和p的分布

式中μq为q的期望，σq为q的方差。

式中μp为p的期望，σp为p的方差。

3 仿真验证与分析

经过上面的计算可知，测量误差会在一定情况下被放大。下面分情况讨论该方法测量角速度的可行性。

3.1 模型计算正确性检验

本文利用已知角速度、角加速度的刚体，计算其上非共线三点的加速度，代入方程(6)，再次计算角速度，验证方程(6)的正确性。

假设有一绕z轴以角速度ω，角加速度β旋转的半径为R的刚体圆柱，如图2所示，在某一时刻，我们计算其上三个特殊点的加速度，再利用方程(6)计算角速度，与原始角速度对比。在xyz系下，A1,A2,A3的坐标，和加速度分别为

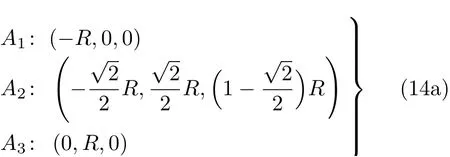
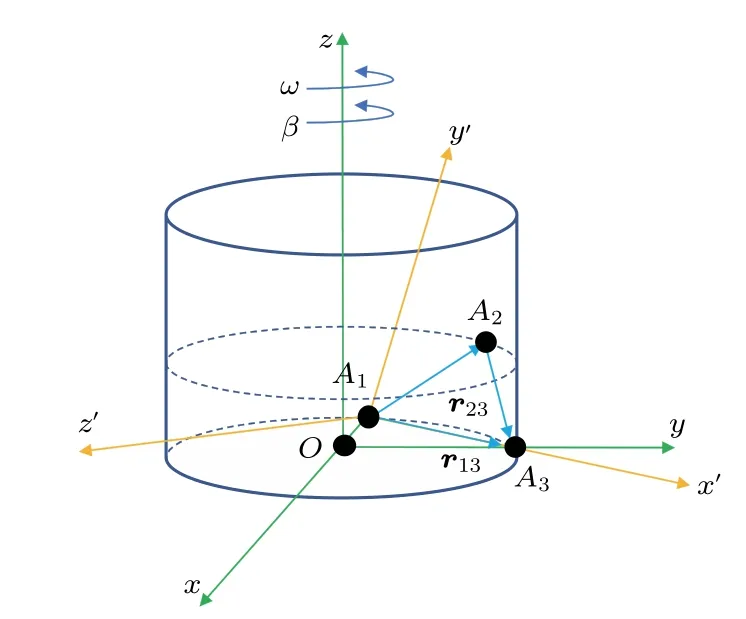
图2 定轴旋转圆柱体上不共线三点示意图

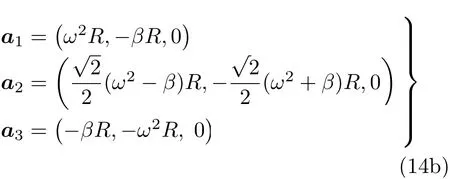
x′y′z′系是以A1为坐标原点，方向为x轴正方向，并以A1A2A3所在平面为x′y′平面建立空间直角坐标系。矢量在两个坐标系之间的变换关系为

在此取法下γ=α= 45°，从而得到矢量坐标变换关系

在新坐标系x′y′z′下加速度为

矢量r13,r23在坐标系x′y′z′下可写为

将方程(17)～(18)带入方程(6)，得到

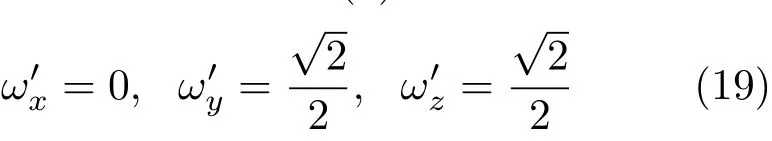
经过坐标逆变换，在原坐标系xyz中得到ω =(0,0,ω)，与我们的模型设定一致，从而证明了我们的计算是正确的。

3.2 高角速度飞行器上的仿真分析

本文参考了文献中的数据，对有较高角速度的飞行器进行模拟仿真。模拟采用的精确数据如下

为了模拟的简洁性，本文不考虑固定的加速度计之间的距离的变化， 即rij为定值， 这里取[r13x,r23x,r23y] = [0.5,0,0.5]m。经过参考加速度计生产商给出的加速度计参数，本文假定，加速度计有一正态分布方差和随机误差。正态分布的σ= 0.049，由此得到三轴仿真加速度计算结果如图3 所示，另外由表1 给出的统计结果可以看出，测量均值与真值接近，且样本标准差较小。

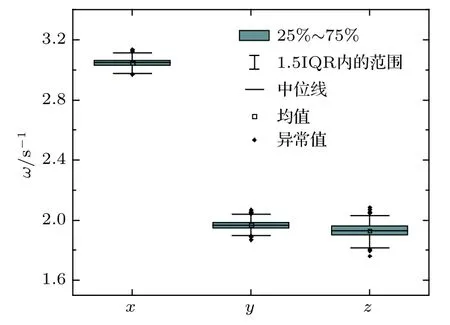
图3 高角速度飞行器x, y, z 方向角速度模拟图

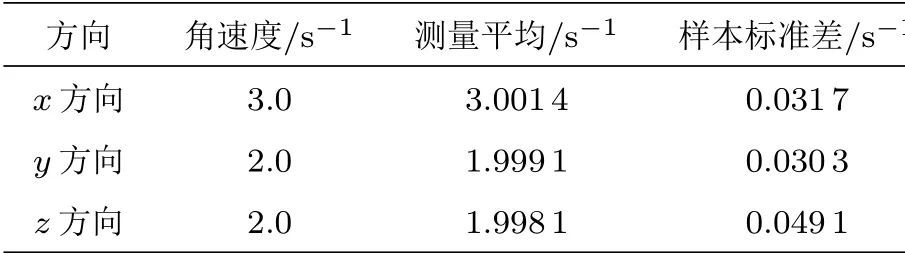
表1 模拟结果

由此可见如果飞行器角速度稳定，可多次测量取平均值，则使用此种方法可以得到较好的结果。然而如果飞行器的角速度变化很频繁，无法多次测量，那么平均值就没有意义了，模拟的极值更有参考价值，模拟结果如表2所示。

表2 高角速度飞行器多组模拟极值的差

它们极值的相对偏差都在5%以上，故而作为瞬时角速度测量，则此方法不太精确。

按次组数据代入上面的方差分析， 可知：σq≈8σ,σp≈4σ，由此也可看出，这种测量角速度的方法会使方差变大。

3.3 稳态卫星上的仿真分析

稳态卫星的角速度很低，约为0.01°/s，对此模型进行模拟，会得到与之前完全不一样的结果。

假设角速度为表3 所列数值，由此计算得a1x-a3x= 4 × 10-10m/s2，可见两个加速度的差在10-10量级，现有加速度计难以完成如此精度的测量。

下面假设存在如此精度的加速度计，依旧进行模拟，模拟结果如图4所示。

表3 低角速度卫星角速度

图4 小角速度卫星x, y, z 角速度分量多组模拟

由图可以看出ωx,ωy皆可求解得到，不过其起伏巨大而且其平均值远远偏离理论值。而ωz的模拟值更是很多都是虚数，只能认为其角速度为零，由此得出的结果也不尽人意。故而，此方法不适用于低角速度的卫星。

4 结论

本文提出一种新颖的测量刚体角速度的方法。利用基点法，通过测量刚体上三个不共线的点的加速度计算出刚体角速度。通过理论分析和数值模拟，本文研究了这种方法的适用范围。得到的结果显示，这种方法在高角速度稳态刚体的角速度测量中可以得到较高的精度(0.05%)。对于其他情形，由于加速度计的测量精度、飞行器本身的振动和计算的截断误差等影响，导致该方法误差较大无法得到精确的瞬时角速度。但是该方法的优点在于，简单廉价。由于本方法并不能准确测量所有情况下的角速度，所以较为适用于飞行器备份测量系统。