有限到无限：基于离散静力平衡推导悬链线方程和梁位移方程

罗雯瑛

(清华大学航天航空学院，北京100084)

1 问题引入

问题：有2n= 100 颗，质量为m的小球等距串在无质量细绳上，绳长为2L，悬挂于A、B点，AB距离为L，如图1 所示。求最低点处细绳的张力、端点处角度。

这是一个静力平衡的问题，对每个小球及每段细绳整体都有受力及力矩平衡。因为要求最低点处绳子的张力，可采用截面法，即将左右两端绳子分离开来，考虑其中一段。由系统的对称性可知左右两段绳子并无差别，并且最低点处绳子是水平的，因此下面考虑右半段绳子，并为方便起见对小球做标号如图2所示。

图1 小球串在细绳上

图2 右半段绳子及对小球的标号

设最低点处细绳的张力为FN0，由于每两个小球之间连接的绳子均为轻绳，因此由力矩平衡可知每段轻绳均是直线。分析前i个小球的受力情况，如图3所示。

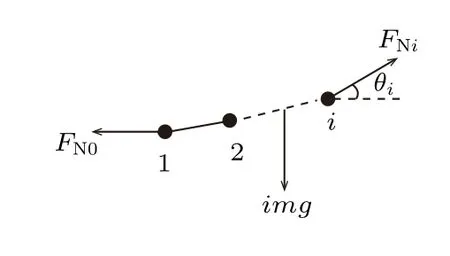
图3 前i 个小球的受力情况

系统有水平和竖直方向受力平衡

记c则由式(1)可得

式(2)中的c是待求量，注意到有条件：AB间距离为L，每段轻绳长度相同且整段绳长为2L，记每段轻绳长度为s，则有s= 2L/(2n+1)。设第i个小球和第i+1 个小球之间的水平距离为xi，即有cosθi=xi/s。因此

由式(2)、式(3)及n=50可数值解得c=0.086 2。

因此最低点处细绳的张力FN0和端点处角度θn分别为

2 悬链线方程的推导

上述问题的讨论对象是一系列离散的质点，而当绳上挂的小球数量趋向于正无穷时，上述模型就可以等效为一有质量且两端固定的悬链线模型，自然地可以利用和上述问题相同的分析方法得到悬链线方程。

当n→∞时，原来的离散模型变为连续模型，之前的分析对象“i个小球”，即相当于连续模型中的一段细绳，对这一段细绳的受力分析可完全类似于对小球的受力分析。设整段绳长为2L，总质量为M，质量线密度为λ，则可根据图4 中一段长l的绳的受力平衡和图中的几何关系解得悬链线方程为

上式中FN0为绳子最底端处的张力。在很多理论力学类教材中都有对式(5)较为详细的推导，本文不再赘述。值得注意的是，式(5)中的参数FN0实际上并不是一个预先已知的量，参考书上给出的悬链线方程一般也就到式(5)为止了，但是在求得的方程中出现一个未知量似乎并不是一件自然的事情。受本文最开始解决的小问题的启发，FN0应当是一个需要被题目所给条件确定的量，下面来确定这个量。

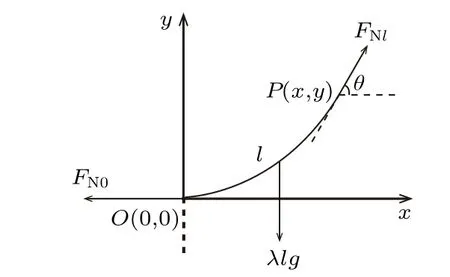
图4 一段长为l 的细绳的受力情况

设绳子固定端(即AB间距离)为2h，则由式(5)可知B端绳子角度的正切为

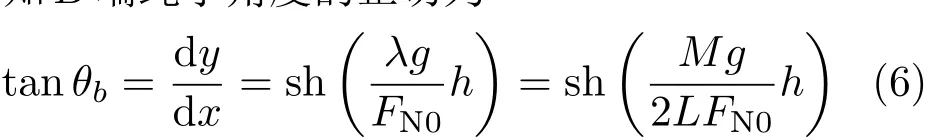
由右半段绳子整体受力平衡可得

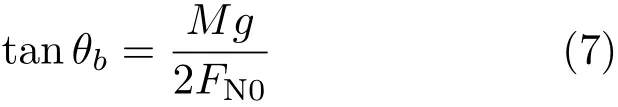
由式(6)、式(7)联立即可得到关于FN0的方程

为了与小问题中的结果比较，取h=L/2，即AB=L，并且小问题中的m是每个小球的质量，可以认为整段绳子的质量M= 2nm= 100m，代入式(8)有

由式(9)可以解得mg/FN0.=0.087 1，与小问题中得到的结果0.086 2 很接近。这也从另一个方面印证了悬链线确实是小问题所讨论的离散模型在n→∞时的极限情况。

3 梁的位移微分方程

前述讨论的是在理论力学中常见的两端固定的悬链线模型，而在材料力学课程以及实际应用中，另一力学模型--梁，是一类重点研究对象。相比柔软的轻绳，梁在位移时除了会产生内应力外还会产生内力矩，但两者在平衡时均满足力平衡和力矩平衡的基本原理。因此若在本文最开始所讨论的小问题基础上，把每个小球节点处加入一个扭簧，使系统能够形成内力矩，就可以根据上文同样的思路导出梁的位移方程，它是加入扭簧后的系统离散模型在n→∞时的极限情况。

3.1 离散情况下对系统的受力分析

为后续讨论方便起见，首先对问题条件如下假定和说明：(1)在加了扭簧的情况下再认为连接两个小球之间的是轻绳不是一个合适的物理模型，可以把“轻绳”替换为“轻杆”。(2) 认为整段轻杆是从水平伸展状态开始在小球重力的作用下变化到最终平衡状态，过程中A和B之间的距离会发生变化，因此不妨设A和B的其中一端是自由的，其中A端固定，B端在水平面自由滑动。

根据对称性，选取系统右半边进行分析，左半边与此类似。对右半边小球标号以及整体受力分析如图5所示。

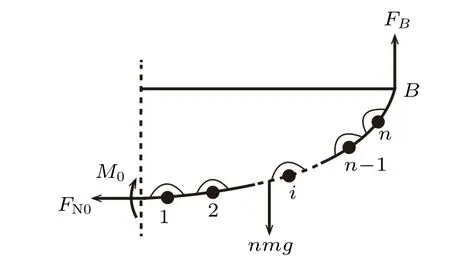
图5 右半边轻杆整体受力情况

由于B点在水平方向自由滑动，因此平衡状态下其对系统提供的约束力竖直向上，设为FB，由AB间整个系统水平方向受力平衡可知A点提供的约束力方向也为竖直向上，设为FA。根据对称性(或力矩平衡)有FA=FB=nmg。

由右半边悬挂线整体竖直方向受力平衡可知最低点处轻杆的内力无竖直方向分量，又由水平方向受力平衡有最低点处轻杆的内力FN0=0，进一步可知整个系统中无水平方向的内力分量。

考虑前i个小球和轻杆组成的系统如图6所示。

图6 前i 个小球和轻杆组成的系统受力情况

由于最低点处轻杆的内力为0，对前i个小球和轻杆组成的系统受力分析有小球i右端的杆(杆i)受到的内力方向竖直向上，设为FQi，且有FQi=img。

再考虑长为s的一小段轻杆(杆i)的力矩平衡，其受力和力矩如图7所示。

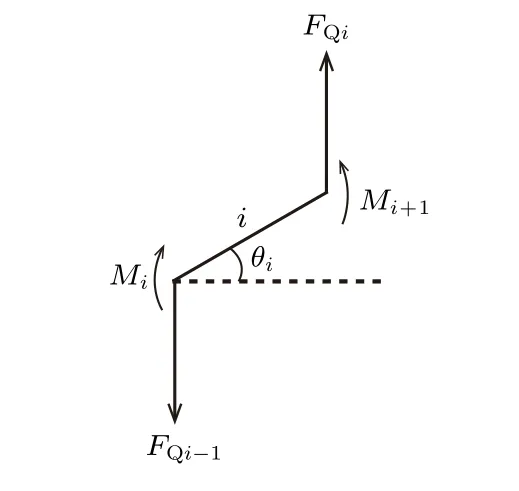
图7 杆i 的受力和力矩情况

对于轻杆i，取球i所在的节点处为参考点应有力矩平衡，即

式(10)中s为每段轻杆的长度，Mi为小球i节点处所加扭簧产生的力矩，即Mi=kΔθi=k(θi-θi-1)。最终可得到一个关于转角θi的递推式

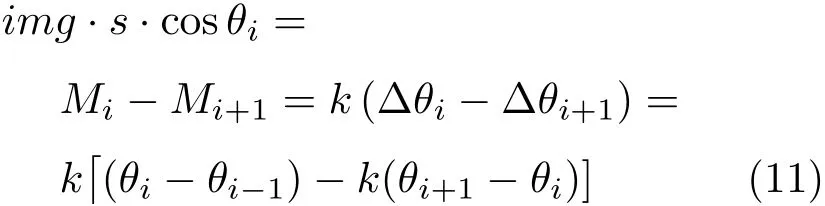
在离散情况下要通过式(11)得到转角θi的表达式很困难，但若将离散情形推广到n→∞的情况，式(11)所示的递推式便会变成一个微分方程，就可以通过求解这一微分方程得到杆平衡时的形状。

3.2 连续情况下梁位移方程的推导

现考虑式(11)两边当n→∞时的情况，实际上此时该模型就是一个在自重下发生位移的简支梁模型，小球的重力在此相当于杆的自重。

式(11)左边的img是前i个小球的重力，在连续模型中，离散模型中的小球替换为一段连续且有质量的杆，设杆的质量线密度为λ，劲度系数线密度(即单位长度上的劲度系数)为K，杆的总长度为2L。考虑长度为l的一段杆，建立如图8 所示的坐标系，其两个端点分别设为O(0,0)和P(x,y)。

图8 长度为l 的一段杆的受力情况

和离散模型中一样，端点P处所受内力FQl方向竖直向上，且有FQl=λlg。离散模型中分析的一段长为s的轻杆在连续模型中应为一段长为dl的微元，如图9所示。

图9 长度为dl 的微元受力和力矩情况

取微元左端为参考点，有力矩平衡

式(12)右端第二项为微元重力提供的力矩，为二阶小量可忽略不计，扭簧产生的力矩大小为Ml=Kθ′(l)，把FQl和Ml的表达式代入式(12)后整理可得

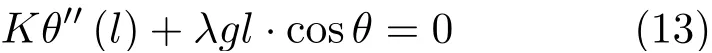
方程(13)即是自重下梁位移的微分方程。但它是一个高阶非齐次微分方程，难以求得解析解。下面主要考虑把该模型与材料力学中推导的梁挠曲微分方程做对比分析，指明其中的物理意义并给出一些近似结果和原方程的数值解。

首先考虑将这一问题与梁发生小位移时的情形类比，并不考虑剪力对变形的影响，在这种情况下弯矩表示为[1-2]上式中M为梁在l处的弯矩，E为梁的杨氏弹性模量，I为梁对z轴的惯性矩。而在上面讨论的问题中，l处的弯矩(即扭簧产生的力矩)为

对比式(14)和式(15)发现，两个弯矩计算方程本质上是一致的，本问题中所设的K实际上就是EI，即梁的弯曲刚度。

以AB中点为坐标原点建立坐标系如图10 所示，下面求杆平衡时在这一坐标系下的近似方程。

图10 小角度弯曲假设下的杆

直接引用梁的挠曲线近似微分方程[1-2]

则在本问题中EI=K，因此对于杆平衡时的形状有微分方程

在当前的近似下杆的自重可以看作是对杆外加了一均匀载荷(x方向均匀分布)λg，这种情况下x处的弯矩满足关系

且有边界条件

因此

由式(17)、式(20)和边界条件可得到悬挂线平衡时的形状满足的方程为

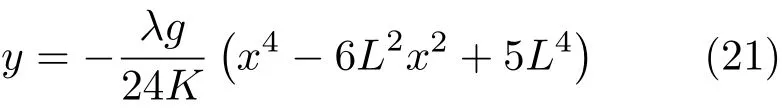
式(21)是在做了大量近似下得到的结果，但不管是在这一问题还是在实际应用中，梁往往不是小变形。为了工程上的实用起见，除了在材料力学课本上对于梁小弯曲的讨论以外，在很多文献中对于梁的大变形情况也都做过一定的研究，这种情况下的微分方程一般给不出解析解(像本文中的式(13))，但可以用各种数值方法对问题进行一定地讨论和解答。例如文献[3-5]对大变形悬臂梁进行了讨论，文献[6-7]求解了不同固定端约束下等截面梁的位移等。

对于式(13)，可以求得它的数值解并据此做出悬挂线的大致形状。取参数E= 2 × 1011Pa，I=2.5×10-11m4，λ=1 kg/m，g=10 N/kg，悬挂线总长度为2L=2 m，则式(13)化为

边界条件为

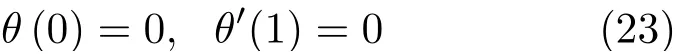
同时也可考虑问题的近似解，在本文所设的参数下式(21)即为()

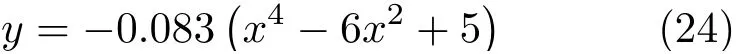
数值解得到的悬挂线形状和由式(24)给出的在小位移近似下悬挂线形状如图11所示。

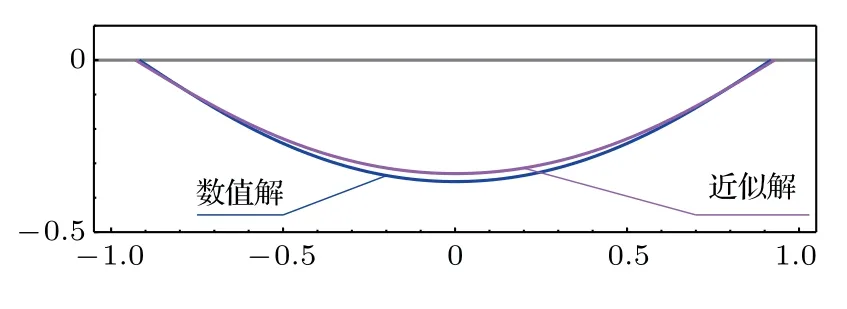
图11 数值解和近似解下的悬挂线形状

可以看到数值解和近似解十分接近，这也说明了对在自重下发生位移的梁做小位移近似是合理的。

4 对梁位移方程的再讨论

对式(13)做进一步分析还能得到一些有趣的结果。

4.1 悬挂线形状的渐变性

在式(13)中记a=λg/K，则

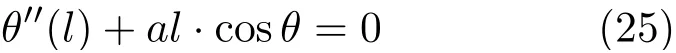
联系前面讨论过的两类问题，即悬链线方程和梁位移方程，它们在离散情况下的区别实际上就是梁比悬链线在每个节点上多了一个扭簧以及有一个端点是自由的。那么在连续情况下，当K→0，也即a→∞时，由方程(25)得到的解应当趋近于一个一端固定、一端自由的悬链线(亦即两条重合的竖直线)。因此本文在下面选取了一系列参数a的值画出对应的悬挂线形状，它们应当能够反映悬挂线从梁到悬链线的形状演变过程。

从图12可以看到，当a越来越大时，悬挂线的形状越来越趋近于两条逐渐接近的竖直线段，也即一端固定、一端自由的悬链线解。

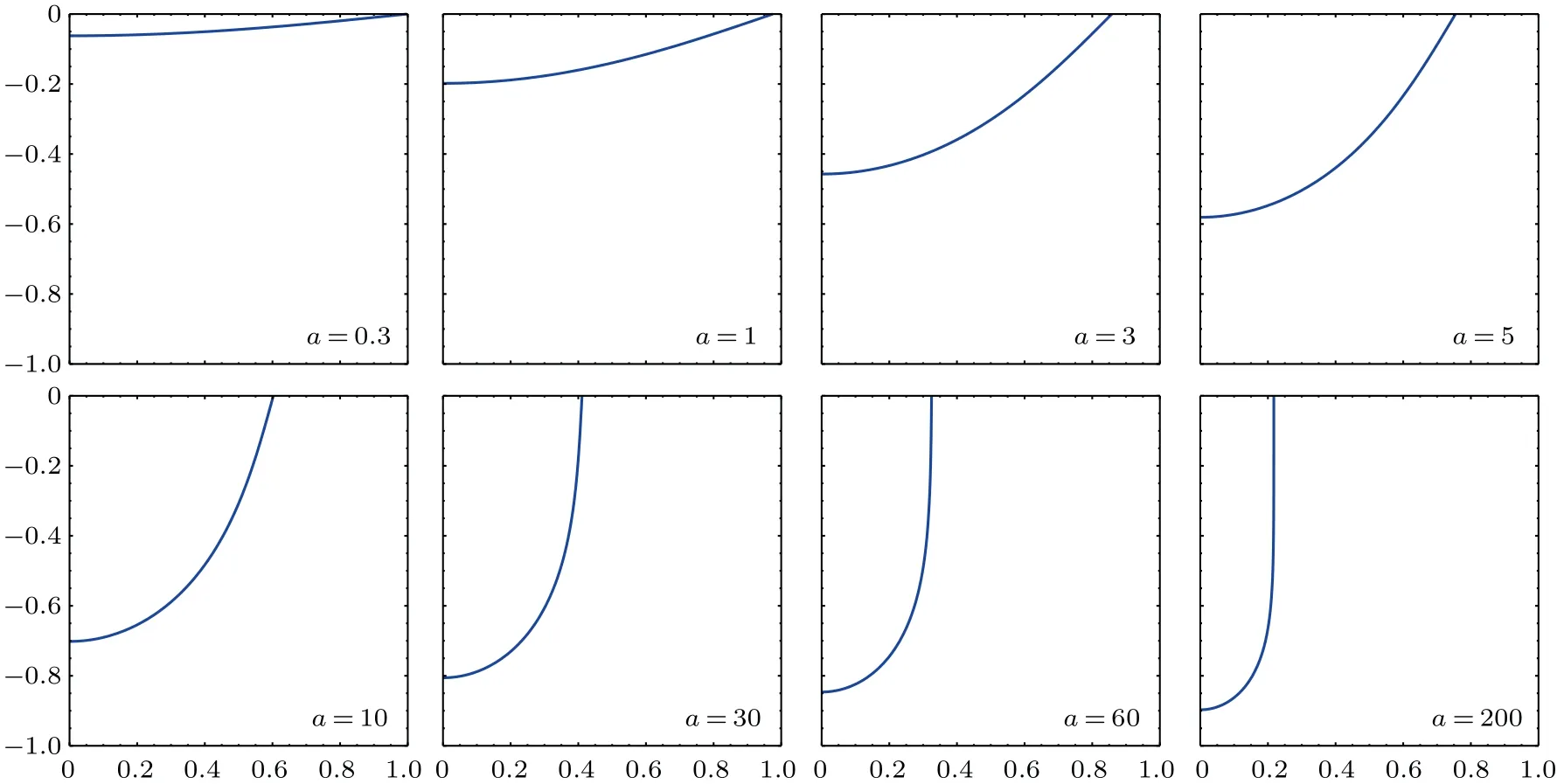
图12 a 取不同值下的悬挂线形状(右半部分)

4.2 方程的多解性

在求由式(13)和一定的边界条件描述的边值问题的数值解时需要对方程中出现的未知参数设定合适的值，在本文前面所设定的参数条件下得到了比较符合正常情况的解，也即方程解的形状是一条悬链线。但是在画图过程中发现当改变参数的值时，解的形状变化很大，并且有时会出现多解的情况，其中有正常的悬挂线解，也会有形状很奇怪的特异解(这种解可能是不稳定解)，正常的悬挂线解是题目所需要的。现仍设悬挂线总长为2 m，边界条件如式(23)所示。则当a= 100 时，由方程(25)得到的各种可能的解的情况如图13所示。

图13 a=100 时的各种可能平衡状态

其中有题目需要的悬挂线解(图13(g))。图13的结果说明由方程(25)描述的系统是一个存在多个平衡态的系统，其中有些平衡态稳定而有些不稳定，从图13 中可以直观地看到很多解是不稳定的。并且经过模拟画图发现解的存在情况和参数a有直接的联系，当a越大时，方程存在的解的形态越多，而当a的取值相对较小，或者说比较接近实际情况(即方程中的参数取得接近真实的梁的参数，例如本文之前在求方程(13)的数值解时所取的参数a= 2)时，系统就只存在正常的悬挂线解了。解的存在情况和参数a的关系如图14所示。

图14 中曲线上的点表示可能的解，横坐标是参数a的值，纵坐标是解的一个边界θ′(0)的值，可以看到随着a越来越大，可能的解确实越来越多。另外，若把所有的悬挂线解标记成红色，并做函数拟合，发现悬挂线解的前段曲线比较符合一次函数的关系，而后段曲线比较符合1/3次方函数的关系。

对这些形状存在性、稳定性以及悬挂线解出现条件的理论分析也是一个有趣且值得讨论的问题。

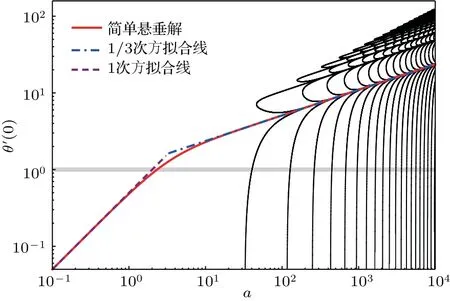
图14 解的存在情况和参数a 的关系

5 结论

本文从对一个简单的力学平衡问题的解答出发，用静力平衡的方法推导了悬链线方程，并通过适当改变题目条件讨论了该模型和梁位移模型的联系。问题讨论过程中从有限的质点模型推广到无限的连续体模型的思想在物理中是很常用且重要的思想，能够使人更清楚地了解模型的物理含义，有时也能带来计算上的方便。文章最后对文中所推导的自重下的梁位移微分方程做了进一步的深入探讨，这对于讨论梁的位移问题具有一定的启发意义。