关于Noether定理1)——分析力学札记之三十

梅凤翔

(北京理工大学力学系，北京100081)

1 Noether的“不变变分问题”

本节介绍Noether 生平，一本关于Noether 定理的科学史书，Noether论文的翻译，Noether的两个定理及其起源，Noether定理和Noether思想的传播等。

1.1 Noether生平

Noether Emmy (1882-1935)，汉译诺特，德国女数学家。自称巴伐利亚族，以色列人。生于埃尔兰根(Erlangen)，其父是德国数学家Noether Max(1844-1921)。1897 年入埃尔兰根女子学院，1900 年入埃尔兰根大学，1904年正式注册为大学生。1907年在不变量理论的著名专家Gordan P (1837-1912)指导下获得博士学位，学位论文为“三元双二次形的形式系统的结构”。1915 年应邀赴格丁根(Göttingen)大学工作，在希尔伯特(Hilbert D, 1862-1943)和克莱因(Klein F, 1849-1925)的支持下，1919 年成为格丁根大学的讲师，1922 年成为编外副教授，1928-1929 年应邀赴莫斯科大学讲学，并出席第八届国际数学家代表大会，1933 年10 月因纳粹政府迫害移居美国，任布林·莫尔(Bryn Mawr)女子学院教授，1934 年起在普林斯顿高级研究所工作。从1907年至1929年用德文发表17篇重要论文。她是抽象代数的奠基人之一，她最重要的论文是“不变变分问题” (Invariante Variationsprobleme，1918)，由此才有了Noether对称性，Noether定理等。

1.2 介绍一本科学史书

Kosmann-Schwarzbach Y 于2011 年 出 版 英 文书《Noether 定理：20 世纪不变性与守恒律》[1]. 这本书的法文版于2004 年和2006 年由巴黎综合工科学校出版，法文书名为Les Théorèmes de Noether.Invariance et lois de conservation au XXesiècle。本书分两部分，第一部分为Noether “不变变分问题”的英译。第二部分为“20 世纪不变性与守恒律：Noether定理的起源与承认”，包括7小节：

(1) Noether定理的起源；

(2) Noether定理；

(3) 用现代和科学史来看Noether定理；

(4) Noether 思想的传播，从Bessel-Hagen 到Hill，1921-1951；

(5) 1950年后Noether第一定理的承认；

(6) 1950年后Noether第二定理的承认；

(7) 1970年后--纯正的推广。

书后附录5个：

(1) 1918 年2 月15 日Noether 给Klein 的 明信片；

(2) 1918年3月12日Noether给Klein的信；

(3) 1921年3月8日Klein给Pauli的信；

(3) 1926年1月7日Noether给Einstein的信；

(5) 给Göttingen数学学会的信。

这本书是研究Noether 定理的科学史，史料较齐全，观点正确，值得一读。资料显示作者在1979-1987年的工作涉及非线性偏微分方程的广义对称性，场论中的动量映射，纤维流形上的矢量场等。这本书没有提到中国学者的相关工作，说明当时中国学者的工作影响力还不够。

1.3 “不变变分问题”的翻译

Noether 的 重 要 论 文 Invariante Variationsprobleme[2]被译成俄文，英文，法文，意大利文和中文。

俄文本出现于Polak LS 1959 年的俄文书《力学的变分原理》(Пoлaк Л С. Бaриaциoнныe Принципы Meхaники. Moсквa: ГИФMЛ, 1959)中, Эмми Neтeр. Инвaриaнтныe Бaриaциoнныe Зaдaч. 由Жaркoв Д Б 翻译。

英文本于1971 年由Tavel MA 翻译为Invariant variational problems (Transport Theory and Statistical Physics，1971，1(3): 186-207)。

法文本是Kosmann-Schwarzbach 的书，2004 年出版。

意大利文本于1960—1990年间由Tonti E 翻译。

中文本于2005 年由梅凤翔根据俄文本翻译，发表在《力学进展》上(2005, 35(1)：116-124)。

一篇论文被译成多种文字反映了Noether 定理的认可度和重要性。

1.4 Noether的两个定理

Noether 在其“不变变分问题”中给出了两个定

理[2].

定理1 如果积分I在群Gρ下是不变的，那么在成为散度的Lagrange表示之间存在ρ个非线性独立组合，反之亦然，这意味着I在群Gρ下是不变的。定理在无限个参数下的极限情形也成立。

定理2 如果积分I在依赖于ρ个任意函数及其至σ阶导数的群G∞ρ下是不变的，那么在Lagrange表示及其至σ阶导数之间存在ρ个等式。反之亦然。

两个定理中的积分I是指高阶Lagrange 函数f的多重积分

函数f是n个独立变量x1,···,xλ,···,xn和μ个依赖变量u1,···,ui,···,uμ及其至某固定k阶导数的函数。

Noether 两个定理非常重要、非常普遍，被认为是变分原理中最重要的两个。Noether第一定理给出对称性(不变性)与守恒量(不变量)之间的关系，对数学，力学和物理学尤为重要。Noether 定理由于变量多，函数多，函数的导数多，而不易读懂。

1.5 Noether定理的起源

Noether 回答了关于对称性与守恒律的两个定理的一些数学问题，这些问题是由Einstein 提出广义相对论的一般协变方程以及由Hilbert 和Klein 寻求新的物理理论而引起的[1]。他们或用于解释新理论中能量-动量张量守恒问题，或使之与已出现的能量守恒律的提法相符合。Noether第一定理使力学和当时已知的狭义相对论中守恒定理得到广泛推广。利用连续变换群的Lie理论，她将微分不变量理论应用于物理的变分方程，提出了特别重要的一般结果。

1.6 Noether定理和Noether思想的传播

文献[1]指出，1950 年之后Noether 定理才得到认可。 在Noether 文章发表后的三年间仅有Bessel-Hagen 的 论 文(1921)，Weitzenböck 的 不 变量理论著作(1923)以及Caurant 和Hilbert 的手册(1924)涉及Noether 的工作。其后有20 世纪30 年代关于量子力学的文献以及Hill 1951 年的文章。1950-1980 年在数学和力学方面涉及Noether 定理的文献[1]列举了如下18篇(部)。

(1) Geĺfand IM (1913-2009)和Fomin SV(1917-1975) 1961 年的俄文书《变分法》，1963 年被译成英文，书中给出变分法的近代表述及其对物理和力学的应用，指出Maxwell 方程实际上是变换的15 参数族(群)下的不变量，即存在5 个守恒律以及由Lorentz 群下方程的不变性导致的10 个守恒律。书中介绍了简单积分的Noether 第一定理，在英文版中涉及Noether第二定理。

(2) Funk P (1886-1969)，Hilbert 的学生，于1962 年出版德文书《变分法及其在物理和技术中的应用》并提到Noether的两个定理。

(3) Souriau JM 在1964 年的法文书《几何与相对论》中写道：“设由变分原理控制的特殊系统，并存在无限小变换使系统不变。Emmy Noether 的方法可以确定某个量，并证明其大小的数值是常数(即设这个量守恒)”。1970 年出版法文书《动力系统的结构》，涉及变分法的变分问题的变换，提出对经典力学的Noether 定理的形式，因为是在流形的框架下，他的提法是现代的。

(4)Lanzos C的英文书《力学的变分原理》(1949年第一版，1962 年第二版，1966 年第三版，1970 年第四版)，前两版未提及Noether的结果，在第三版和第四版的前言中，他写道：“本版不同于前版加上了一节关于Noether 不变变分问题。Noether 的原始论文不易弄懂。”

(5) Rund H 的英文书《变分法中的Hamilton-Jacobi 理论：它在数学和物理中的作用》(1966)给出Noether 定理的表述，先是对单个独立变量，而后对多重积分问题。

(6) Trautman A 于1950 年代开始研究广义相对论中的守恒律，他是首先用近代数学语言，即流形的语言，介绍Noether的论文。

(7) Edelen DGB 的英文书《场的非局部变分和局部不变性》(1969)，考虑作用在独立变量流形上的坐标变换或点变换下泛函的几何性质，讨论了Noether定理的两种情形。

(8) Smale S (1930-)1970 年的论文“拓扑与力学”，在“力学中的对称”一节中，他首先断言“Noether 是阐明对称性与积分类系的大可信赖的人”，而后利用位形流形的切丛提出有对称的力学系统并引入角动量的概念。他的方法是表示为切丛的纯Lagrange 方程和表示为余切丛的Hamilton 形式之间的中间方法。

(9) Sniatycki JS在1970年的论文“Lagrange形式中经典场论的几何结构”中，将Noether 的结果转换为用流形和射丛语言表示的不变几何形式。

(10) Krupka D于1971年和1973年发表的论文涉及纤维流形中变分问题的几何形象。

(11) Goldschmidt H和Stenberg S在1973年的长文“变分法中的Hamilton-Cartan 形式”中，利用纤维流形和射丛仿射结构，给出多变量变分法的几何解释，对发展Noether 定理和Bessel-Hagen 推广是重要的一步。

(12) Garcia PL 在1974 年的论文“变分法中的Poincaré-Cartan 不变量”中，强调不变变分问题的现代“流形代数”和老的“Noether 定理”之间概念的一致化, 但未引用Noether的文章。

(13) Arnold VI (1937-2010)的书《经典力学的数学方法》(俄文1974, 1979；法文1976；英文1978,1989；德文1988；中文1992)中有一节“Noether 定理”，指出由Lagrange函数的不变性可导出守恒量。

(14) Marsden JE (1942-2010) 1974，1978 年的工作跟随Souriau 将Noether 定理称为守恒定理的Hamilton表示。

(15) Logan JD 于1970 年写出博士学位论文“Noether 定理和变分法”， 他是Drobot 的学生，Drobot 是Steinhaus 的学生，Steinhaus 是Hilbert 的学生。1977年的“不变变分原理”中指出“Noether 定理已成为近代场论的基石之一”。

(16) Ibragimov NH 在1969—1983 年的工作中涉及不变变分问题和守恒律，Noether 等式，应用于数学物理的变换群等。

(17) Kijowski J 和Tulczyjew WM在1979年的《场论的辛构架》中提供了导出物理理论变分公式的系统方法，基于辛流形的Lagrange 子流形的概念发展了对粒子物理和场论的新的物理理论。

(18) Goldstein H (1922-2015)的《经典力学》(1950, 1980, 2002)第一版讨论了力学中某些守恒定理，但未提及Noether定理。

以上是文献[1]列举的18 篇(部)关于Noether定理对数学和力学的应用，大多为20 世纪60∼70 年代的工作，大多涉及流形语言，而作者都有较高知名度，如Souriau JM，Smale S，Arnold VI，Marsden JE, Tulczyjew WM 等，其中最后两位是“分析力学近代发展讨论会”(1982，Torino)学术委员会成员。

2 经典力学中的Noether定理

本节讨论经典力学中的Noether 定理， 包括Hamilton 作用量的不变性，含速度变换下的Noether 定理，完整非保守系统的Noether 定理，非完整系统的Noether 定理，Birkhoff系统的Noether定理，被积函数用动能和势能的高阶导数替代的情形，Noether等式的弱化，对连续介质力学的应用，对Noether对称性的理解等。

2.1 Hamilton作用量的不变性

经典Noether 定理出现于一些教材中，如文献[3-6]。在Noether 的积分I中独立变量取为时间，依赖变量取为广义坐标，即

被积函数取为Lagrange 函数，即f=L(t,q,˙q)，则积分I成为Hamilton作用量

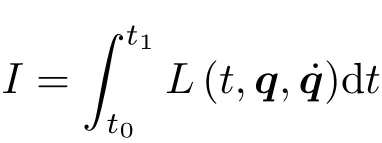
取无限小变换

其中ε为一无限小参数，ξ0，ξs为无限小生成元。表示不变变分问题的Noether等式有形式

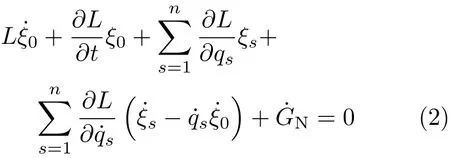
其中GN为规范函数。Noether守恒量为

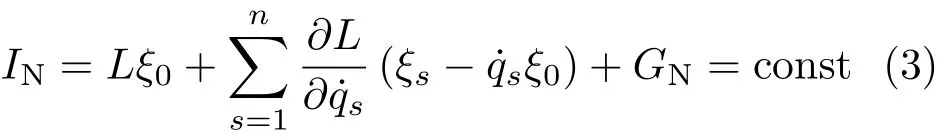
这样给出经典Noether 定理：如果无限小变换式(1)的生成元ξ0，ξs和规范函数GN满足Noether 等式(2)，则Lagrange系统

有Noether守恒量式(3)。

“经典Noether 定理”一词由文献[7]提出。利用经典Noether 定理不仅可得到力学中的基本守恒律，还可以得到更多的守恒律。如果Lagrange 函数L不含t，即

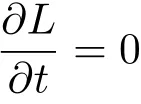
取生成元

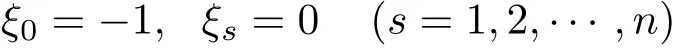
则由式(2)，得到

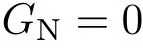
式(3)给出

这就是广义能量积分。如果q1为循环坐标，即

取生成元为

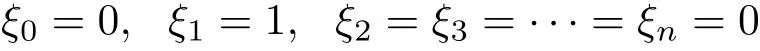
则式(2)给出

式(3)给出

这就是循环积分，代表广义动量守恒。基本守恒律也可直接由Lagrange方程(4)导出。

设单自由度系统的Lagrange函数为

它代表Emden方程

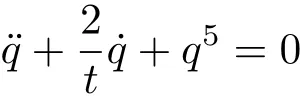
Noether等式(2)给出

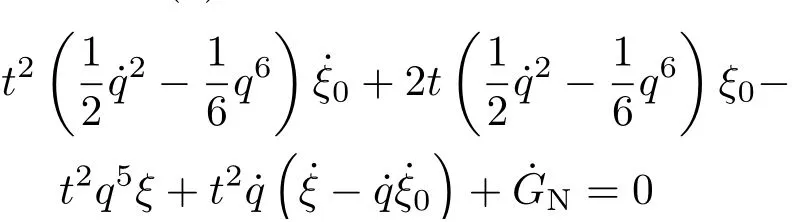
可找到它的解

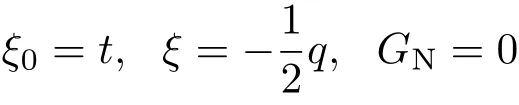
守恒量式(3)给出

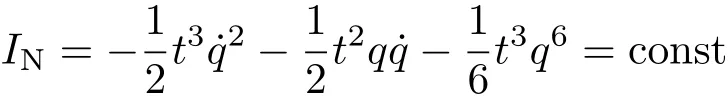
这样的守恒量还不能由Lagrange方程导出。

经典Noether 定理是Noether 第一定理对Lagrange系统的一个应用，由此，不仅可直接导出力学的基本守恒律，还可以找到更多的守恒律。

2.2 含速度变换下的Noether 定理

经典Noether定理的变换是不含速度的，这符合Noether 的原意。南斯拉夫学者Djukić 和Vujanović将变换式(1)推广到含速度情形[8]，即代替式(1)，有

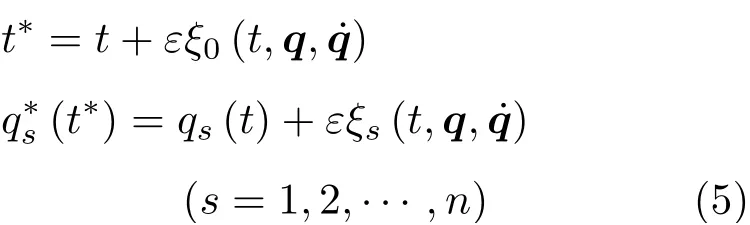
此时，对Lagrange 系统，Noether 等式仍为式(2)，Noether 守恒量仍为式(3)，不同的是相应的Killing方程。这种推广有利于找到更多的守恒量。例如，Kepler问题的Lagrange 函数为

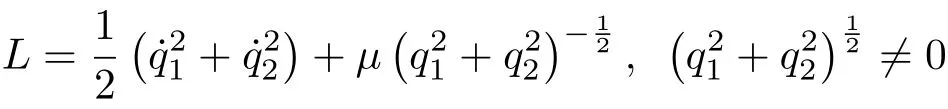
Noether等式(2)给出

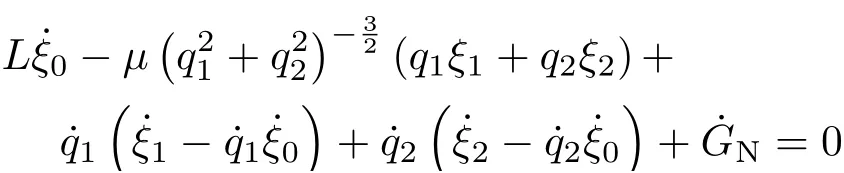
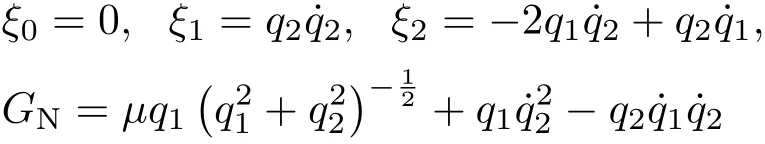
可找到它的解守恒量式(3)给出

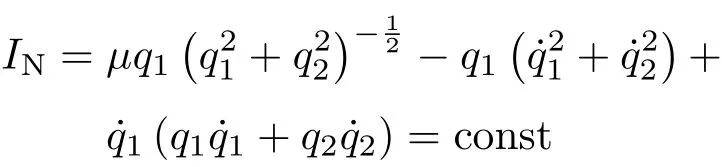
它是Runge-Lenz矢量分量的守恒量。

这种推广已被广泛认可，如文献[6,9-10]。

2.3 完整非保守系统的Noether 定理

经典Noether 定理是对Lagrange 系统给出的。如果Hamilton作用量S的全变分满足

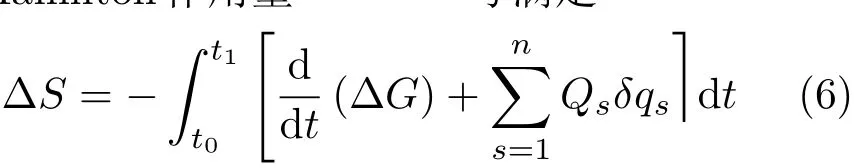
其中ΔG=εGN,Qs(s=1,2,···,n)为非势广义力，则称变换为广义准对称变换。此时对系统

Noether等式成为

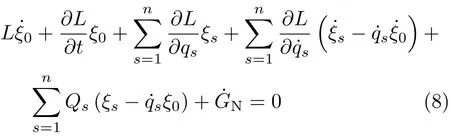
而守恒量仍有式(3)。式(8)称为Noether-Bessel-Hagen方程。

以 上 结 果 由Djukić 和Vujanović 给 出[8]。Vujanović BD 是南斯拉夫著名学者，1982 年6 月由IUTAM 和ISIMM 在意大利都灵举办“分析力学近代发展讨论会”，Vujanović 为学术委员会成员。有关完整非保守系统的工作还可参见文献[6,9,11]。Noether 定理的这种推广可以解决完整非保守系统的对称性与守恒量问题。

2.4 非完整系统的Noether定理

微分方程为

约束方程为

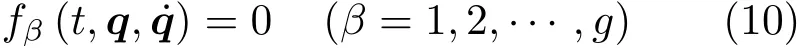
在运动微分方程积分之前，可由方程(9)和(10)求出约束乘子λβ为t,q,˙q 的函数，令与非完整系统方程(9)和(10)相应的完整系统的方程为

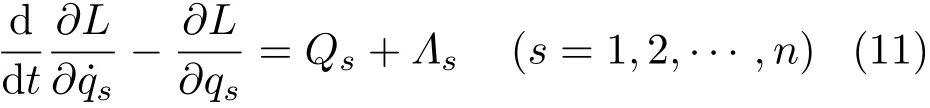
此时Noether等式有形式

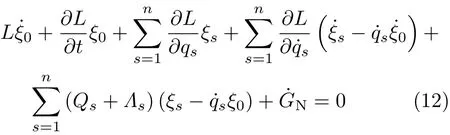
非完整约束方程(10)对生成元ξ0,ξs的限制为

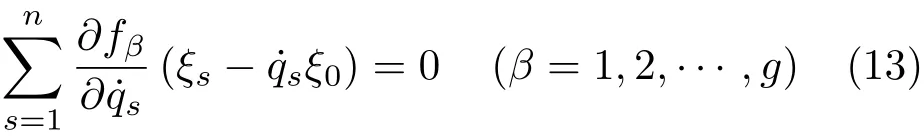
相应的守恒量仍为式(3)。如果无限小生成元ξ0,ξs和规范函数GN满足式(12)，则相应完整系统方程(11)存在Noether 守恒量式(3)。进而如果还满足限制方程(13)，则存在非完整系统的Noether守恒量式

(3)。

例如，Appell-Hamel的Lagrange函数和非完整约束分别为

方程(9)给出

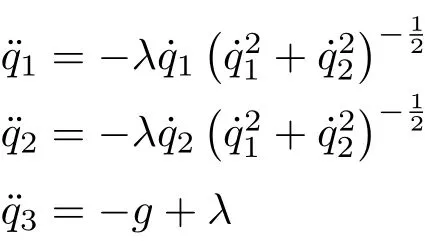
可求出约束乘子

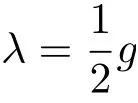
以及非完整约束力

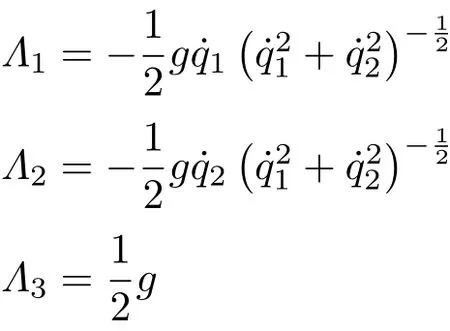
Noether等式(12)给出

限制方程(13)给出

可找到如下解

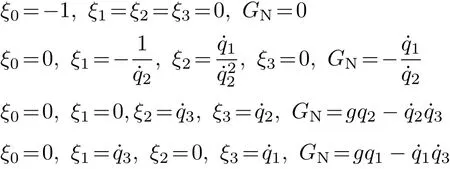
相应的守恒量分别为

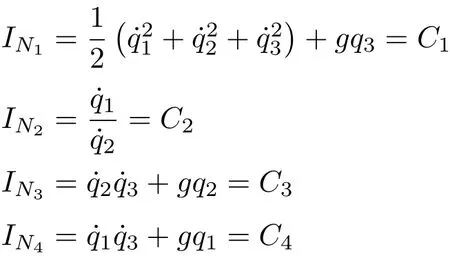
有关非完整系统的Noether定理，见文献[6,9,12-15]。

2.5 Birkhoff系统的Noether定理

以Pfaff作用量替代Hamilton 作用量，可建立Birkhoff系统的Noether定理。

令

Noether等式(2)成为[16]

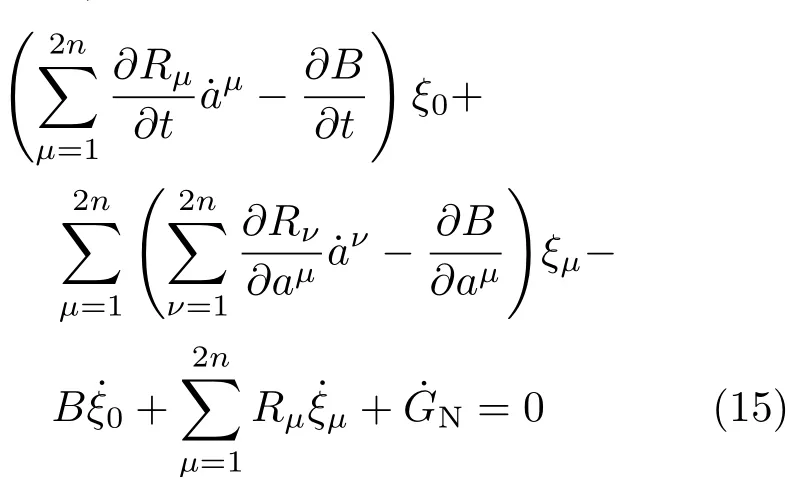
Noether守恒量方程(3)成为文献[17]由直接变分也得到上述结果。进而，对广义Birkhoff方程

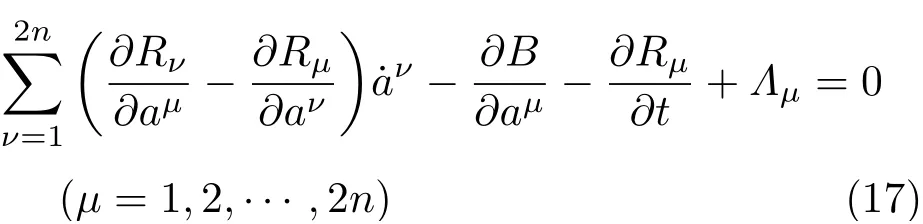
在式(15)左端应添加一项

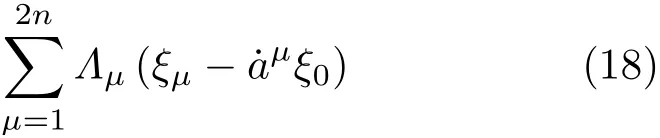
而守恒量仍为式(16)。

2.6 被积函数用动能和势能高阶导数替代的情形

泛函表示为

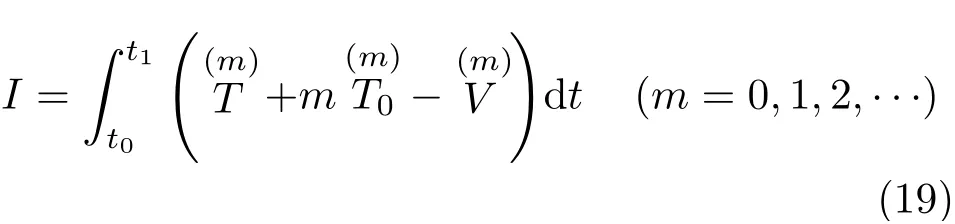
其中T为系统动能，V为系统势能，而

由式(19)出发可建立高阶系统的Noether 定理[9]。当m=0时，式(19)为Hamilton作用量。

2.7 Noether等式的弱化

将Noether等式(8)改写为下列形式

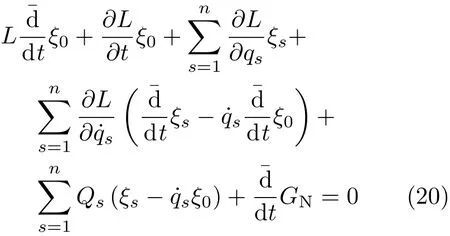
其中

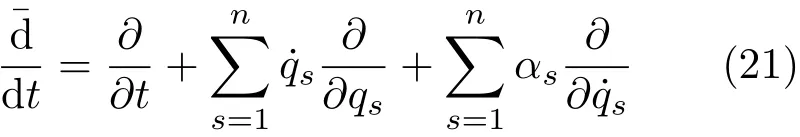
方程为

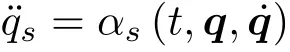
即在Noether 等式中出现¨qs时以αs替代，这样的Noether 等式称为弱Noether 等式[18]。如果生成元ξ0，ξs和规范函数GN不依赖于速度，则弱Noether等式(20)成为Noether 等式(8)。如果ξ0，ξs，GN依赖于速度，两者会有所不同。由弱Noether 对称性也可找到守恒量式(3)。例如，对二自由度系统

Noether等式(8)给出

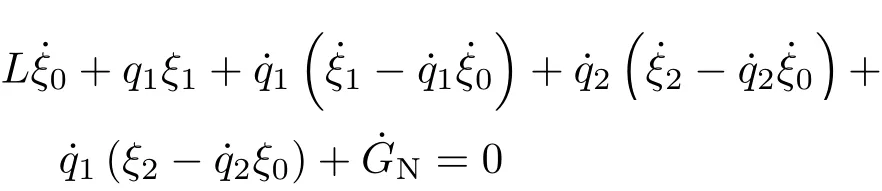
弱Noether等式(20)给出

生成元和规范函数取为

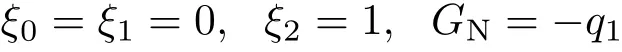
它们满足两个Noether 等式。这种对称性是Noether的，也是弱Noether的。生成元取为

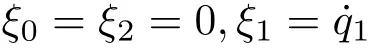
由Noether等式得

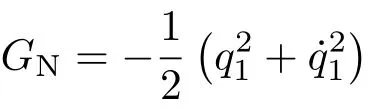
由弱Noether等式得

相应的守恒量分别为

两者稍有不同。

生成元取为

由弱Noether等式得

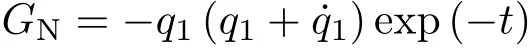
但由Noether等式找不到相应的规范函数GN。

2.8 对连续介质力学的应用

专著[9]介绍了连续介质力学的Noether定理。

2.9 对Noether对称性的一种理解

有些作者将Noether 对称性理解为Lagrange 函数的不变性。

Arnold 在其著作中给出如下Noether 定理：如果系统(M,L)允许有单参数微分同胚群hs:M→M,s∈R，那么对应L的Lagrange 方程有一个第一积分I:TM→R。在M的局部坐标下，积分I写成形式[19]

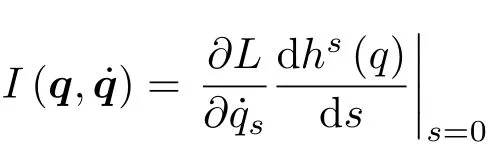
José 和Saletan 写道：“如果一个Lagrange 函数在一变换族下是不变的，其动力学系统有一运动常数，那么它可由Lagrange函数和变换来找到。”[20]

这里的变换，时间是不变的。在时间不变的变换下，Lagrange函数的不变性意味着

其中

而Noether等式为

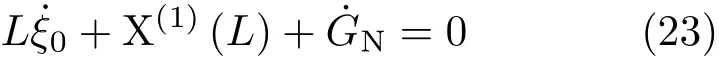
由式(22)给出的守恒量为

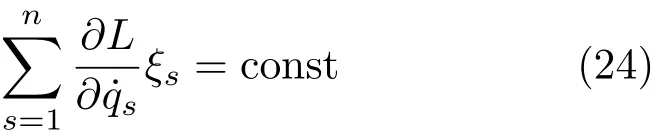
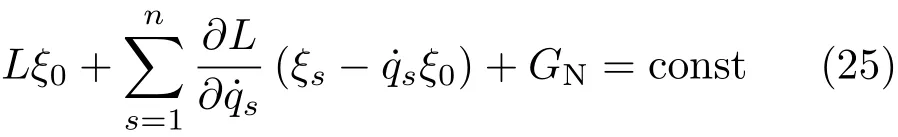
由式(23)给出的守恒量为显然, Lagrange 函数的不变性与经典Noether 定理的Noether 对称性以及它们导出的守恒量一般是不一样的。例如，对Lagrange系统

取生成元为

则式(22)满足，由式(23)得

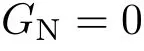
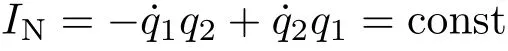
守恒量式(24)和式(25)都给出因此，这个对称性是Lagrange 函数的不变性，也是Noether对称性。

取生成元

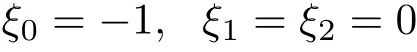
它不是Lagrange 函数的不变性，而是Noether 对称性。守恒量式(25)给出

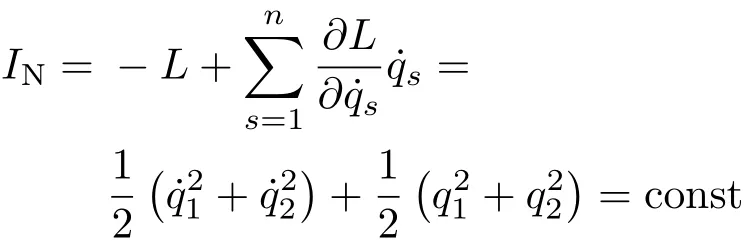
2.10 各类Noether 定理

列举一些Noether 定理， 包括对经典力学的Noether 定理[21]；对单面约束系统的Noether定 理[22-24]； 对Vacco 动 力 学 的Noether 定 理[25]；Poincaré-Chetaev 方 程 的Noether 定 理[26]；对 相对论性系统的Noether 定理[27-29]；对高阶系统的Noether 定理[30]；对广义力学系统的Noether 定理[31]；对物理系统的Noether 定理[32-33]等。此外Olver的专著有十处提到了Noether定理[34]。

文献[1]列举了1970 年之后Noether 定理的纯正(genuine)推广，包括射丛和广义对称性，守恒律的特征与第一定理的逆，形式变分学，非变分方程的对称性与守恒律等。本节所指经典力学中的Noether定理不是Noether 定理的纯正推广，而是Noether 第一定理在经典力学中的应用。这些在文献[1]中几乎都未提及。

3 结语

Polak 指出,力学的变分原理的应用和物理意义的基础是两个定理：Hilbert 独立性定理和Noether定理。前一个定理给出变分原理的数学论据，后一个定理揭示出它的物理意义。

Noether在1918年的论文“不变变分问题”中给出的两个定理，形式简单而思想深刻，需要认真学习、领会。第一定理对分析力学尤为重要，利用Noether 定理不仅可以找到牛顿力学的经典守恒律以及Lagrange 力学的广义动量守恒律和广义能量守恒律，而且可找到更多的守恒律。力学系统的守恒律对研究力学系统的动力学行为，稳定性，计算等都有指导意义。Noether 的工作和她的学术思想必将进一步发扬光大。