一种轿车车轮应力状态测量与分析方法1)
2020-03-16任念祖杨清淞杜天强刘振国
刘 程 任念祖 杨清淞 陈 超 杜天强 田 程 刘振国
(中国汽车技术研究中心有限公司试验所零部件研究部,天津300300)
轿车车轮是车辆中最重要的安全部件之一。如果车辆在行驶过程中车轮出现疲劳破坏,那么会直接影响到驾乘人员的生命财产安全,因此可靠性设计是车轮设计最重要的内容之一[1]。近些年随着用户对车辆燃油经济性需求的提高,对车轮的轻量化水平提出了更高要求,为此工程师们通过设计车轮新结构,应用更多新材料、新工艺来达到轻量化目的[2]。这些车轮新产品的出现,使得其可靠性设计也面临着新的挑战。当前车轮可靠性设计方法主要分为基于仿真计算的结构优化设计和基于试验的产品优化设计两个方面[3-5]。在车轮设计初期,由于车轮的轮辋直接与轮胎接触,其结构形式由标准化的轮胎尺寸确定,一般会利用有限元结构优化方法对轮辐结构进行优化设计,通过有限元可以计算车轮在特定载荷下的应力状态[6],但是车轮最终的疲劳强度不仅与基本结构有关,还与车轮的加工工艺以及使用条件有关。车轮的最终受力状态是由多种因素共同作用的结果[7]。而仿真计算过程中并不能完全考虑到这些因素[8-11]。另外一种为台架可靠性试验方法,利用台架试验考核车轮典型工况下的疲劳寿命,试验样品为最终的产品状态,可以真实地反映车轮载荷状态。但是由于试验过程中很难对车轮所有位置的载荷状态进行测量,一般只是根据工程经验对一些特殊位置的单向载荷进行测量作为设计优化的依据[12-13]。
针对以上问题,本文建立了一种基于仿真和试验相结合的方法,分析车轮受力状态。本文首先分析了车轮在使用过程中的载荷状态,然后依据载荷状态确立了车轮两种可靠性试验方法,接着根据台架试验方法原理建立车轮有限元模型,预测在可靠性试验过程中车轮危险点出现的位置。其次是利用应变花测量危险点处不同试验条件下的应变状态。最后,对车轮在不同试验条件下的应力状态进行对比分析,为车轮的优化设计提供指导。
1 轿车车轮典型工况载荷分布
轿车车轮在使用过程中轮辋与轮胎配合使用,车轮中心位置与轮毂相连接。在车辆行驶过程中轮胎的载荷通过轮辋、轮辐、轮心将载荷传递给轮毂,然后通过轮毂将载荷传递到车辆悬架以及车身,同时车身载荷也会通过轮毂传递给车轮,为此车轮在使用过程中会承受三个方向的平动载荷和三个方向的转动载荷。不同行驶状态,车轮对应承受载荷也不同,下面将对直线和转弯行驶两种典型工况下车轮的载荷状态进行分析。
1.1 直线行驶工况
车辆在使用过程中,绝大部分行驶状态为直线行驶[14],有研究表明在直线匀速行驶工况下,车轮的垂向受力分析如图1 所示,轮毂传递的驱动力矩以及轮胎产生的摩擦力矩较小,车轮主要承受垂向载荷。此时车轮承受车身传递给轮毂的垂向载荷Fg,以及轮胎传递给车轮的垂向载荷Fv,可表示为

式中,FT为车轮静态垂向载荷,k车轮动态载荷系数。
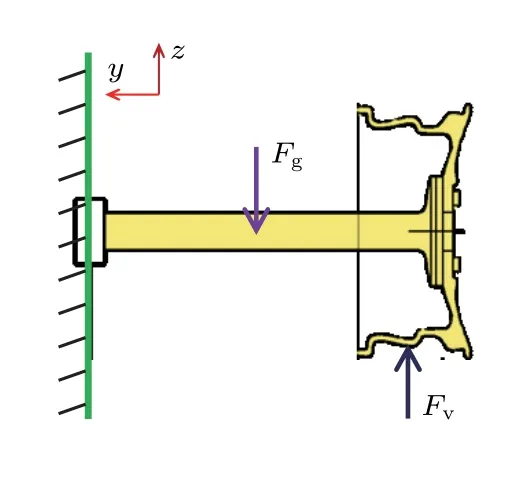
图1 车轮直线行驶工况受力分析
1.2 转弯行驶工况
车轮使用过程中另外一个较多的工况为转弯行驶工况[14]。此工况下车轮的受力如图2所示,此时车轮不仅需要承受垂向载荷,也需要承受侧向载荷。假设轮胎与车轮之间的综合作用点位置为点C,此时车轮除了承受垂向载荷Fg,侧向载荷Fy外,在车轮中心位置也需要承载轮胎载荷对车轮中心位置产生的弯曲力矩
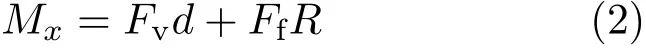
式中,Fv为轮胎传递给车轮的动态垂向载荷,Ff为轮胎传递给车轮的侧向载荷,d为车轮偏置距,R为车轮滚动半径。

图2 车轮转弯行驶工况受力分析
2 轿车车轮可靠性台架试验方法
为了考核车轮使用过程中直线行驶和转弯行驶两种状态下的可靠性,工程师设计了车轮的两种典型的可靠性试验,具体试验原理及试验方法如下。
2.1 径向疲劳台架试验方法
径向疲劳的试验目标是为了考察直线行驶车轮承受径向载荷时,对应的疲劳可靠性能力,根据文献[15]中要求,试验时通过设备轮毂将车轮压在转鼓表面,转鼓与车轮之间的载荷为

式中,Fvmax为车轮或者汽车制造厂规定的车最大径向载荷数,K为强化试验系数,具体取值可参考文献[15]。
式(1)与式(3)形式相同,只是此试验载荷考察的为车轮极限工况下的载荷。
2.2 弯曲疲劳台架试验方法
车轮弯曲疲劳试验台,主要是考察车轮在转弯状态下的车轮所能够承受弯曲载荷的能力,根据文献[15]中要求,试验时车轮承受的弯曲载荷为

式中,R为轮胎静负荷半径,m;d为车轮偏距,m;μ为摩擦系数;Fvmax为车轮最大垂直静载荷,N;S为试验强化系数。其中摩擦系数μ和试验强化系数S一般根据不同的设计要求确定,具体可参考文献[15]。
式(4)与式(2)之间的主要区别是Fvmaxd为最大径向载荷产生的弯曲力矩,μFvmaxR为最侧向力产生的弯曲力矩,即此试验是考察车轮在极限工况下对应的弯曲疲劳载荷。
试验时将车轮轮缘固定,通过在车轮轴端施加力F来产生力矩M,力F的计算公式为

式中,L为试验设备加载臂长度。
3 轿车车轮可靠性有限元计算方法
通过上节中分析车轮疲劳试验原理及过程可以看出,车轮不同的试验项目考察车轮不同部位的载荷状态,如车轮的径向疲劳试验主要考察车轮轮辋承受载荷的能力,而弯曲疲劳试验主要考察车轮轮辐承受弯曲载荷的能力。并且以上疲劳试验只是作为车轮最后的可靠性能力的考核,并不能直接指导设计,只有了解在这些试验状态下的应力分布才能为进一步的优化设计提供依据。因此本文提出利用台架试验测量车轮在不同工况下的应力分布,以此为依据来对车轮疲劳寿命进行预测。但是台架测量时,工程师并不知道车轮应力集中点的位置。针对此问题,本文提出了一种有限元计算方法来预测车轮疲劳试验时应力分布危险点位置,并作为车轮的疲劳台架应力试验测点位置。下面主要针对径向疲劳和弯曲疲劳两种有限元仿真计算方法进行简要阐述。
3.1 径向疲劳有限元仿真
根据1.1 和2.1 节中描述原理可以看出,台架试验过程中转鼓通过轮胎将载荷传递给车轮,为了简化仿真复杂度,一般将轮胎与车轮之间的相互作用力简化为轮胎作用在车轮轮辋位置的接触力。但是精确表述轮胎对轮辋的压力分布是困难的,参考文献[16],可以在轮胎与转鼓挤压接触的位置将径向负荷近似为余弦载荷。假设在车轮平面内加载压力在2θ角度内沿垂直方向为余弦函数分布,在轮辋两侧胎圈座的轴向方向为均匀分布。如图3 所示,假设两侧车轮胎圈位置的载荷为对称分布,即每一侧的载荷为

式中,Fr为弯曲疲劳台架试验对应的径向载荷。
另一方面,根据轮胎与车轮之间的载荷分布定义,轮胎胎圈位置每一侧载荷可表示为

式中,B为胎圈宽度,2θ0为轮胎与车轮载荷作用角度范围,rb为轮胎胎圈的半径。A为任意位移轮胎传递给车轮胎圈位置的压力分布幅值,可定义为
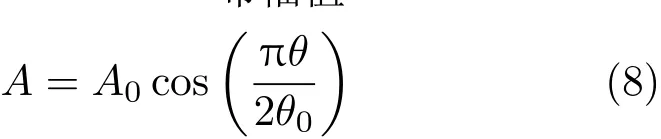
根据式(7)和式(8),即可以得到车轮胎圈位置的压力分布最大幅值为

根据文献[16],一般假设θ0= 2πup/9,根据所研究车轮的尺寸,压力的最大幅值A0为1.4 MPa。
确定载荷后,接下来就是对车轮进行有限元网格划分。由于车轮的结构复杂,网格划分之前需要进行几何清理,将几何体中的小圆角与倒角进行清理,最后利用软件Hypermesh 进行四面体网格划分,网格的大小为5 mm,最小尺寸控制在2 mm,最后得到车轮的网格模型。接下来需要定义模型的材料属性,本文研究ZL101A-1 铝合金车轮,其材料的密度为2.7 t/m3,弹性模量为27 GPa,泊松比为0.32。根据本文所研究车轮的结构特点,在径向载荷下,车轮的最大辐孔中间位置,也就是车轮轮辋胎圈承受压力幅值最大的位置,承受载荷能力最弱,容易出现应力集中。在车轮有限元模型上加载连续的余弦压力较繁琐,仿真时可以将其离散为有限段,本文中设置为20 段,每一段内加载均匀压力,压力幅值为这一段内的平均幅值。同时为了模拟轮胎的充气压力对车轮表面的作用,在轮辋表面与轮胎内气体接触的位置加载均匀的压力载荷。本文根据文献[15]的要求以及所研究车轮的型号,定义施加的充气压力为0.45 MPa。为与径向疲劳可靠性试验状态一致,试验过程中约束轮辐位置的所有螺栓孔的自由度。建立有限元模型并提交给求解软件的静态求解器,最后可以得到车轮在此载荷下的应力分布状态。
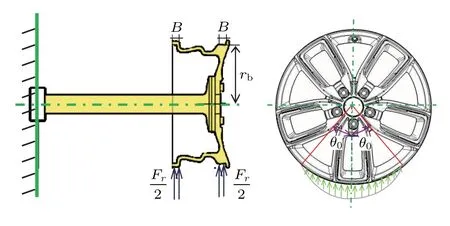
图3 径向疲劳试验时车轮载荷简化
如图4 所示,可以看出车轮的轮辋位置出现了较大的应力集中点,而轮辐位置的变形量较小。此工况下车轮的应力集中点主要集中在车轮轮辋上靠近车轮反面的边缘位置,同时在轮辐位置也有较大的应力集中。
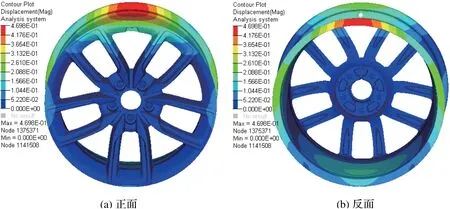
图4 径向疲劳应变仿真分析
3.2 弯曲疲劳有限元仿真
根据1.1 和2.1 节中描述原理,在车轮弯曲疲劳试验时车轮受力分析的有限元模型中,装配0.9 m长的加载轴,将该模型导入软件中进行有限元前处理。采用四面体单元对装配体模型进行网格划分,车轮模型的单元大小为5 mm,允许最小尺寸为2 mm。依据文献[15] 的方法要求,对轮辋内侧外沿节点施加固定约束。加载轴的法兰面和车轮安装面之间的螺栓连接用一维单元模拟。在加载轴末端施加垂直于加载轴轴向的力2747 N,力的方向为指向轮辐的最大通孔位置的中心线上。
设置分析步骤,最后将静态分析模型提交给求解器,对应的车轮应力分布如图5 所示,可以看出径向疲劳试验中,车轮的主要变形位置位于轮辐上。弯曲疲劳模拟中车轮轮辐和轮心位置变形较大,轮辋位置变形较小。可以看出在轮辐与轮心的连接位置出现了应力集中,同时在车轮螺栓安装位置存在应力集中。
在系统数字化和智能化的飞速发展的今天,《信号与系统》理论和数字信号处理技术的应用随处可见。特别是数字信号处理理论的学习对于通信类专业的学生尤为重要。近几年来,全国很多高校学生扩招,本科学生水平良莠不齐,数字信号处理和信号系统课程对数学能力的要求比较高等,学生学习成绩和效果不理想。为了改善目前这种状况,提高学生理论和实践的能力,对于该门课程的教学内容、方法也在不断更新,特别是教学方法。为避免上述的不利因素,提出MATLAB案例实践教学的方法进行探索,将会具有很强的进步意义。
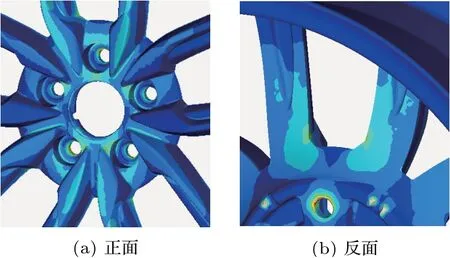
图5 弯曲疲劳应力分布局部放大
4 轿车车轮危险点位置应力测量
通过以上有限元分析可以得出:如图6 所示,从图中可以看出轮辐位置的1,2,3 点容易出现应力集中,并且在轮辐的倒角位置4,以及轮心位置5 也有可能出现应力最大点。在径向疲劳仿真中,可以看出轮胎与车轮胎圈座接触的位置会出现应力集中,但由于此位置应变片无法粘贴,为此在胎圈座正对的车轮内部作为应力测量点6。
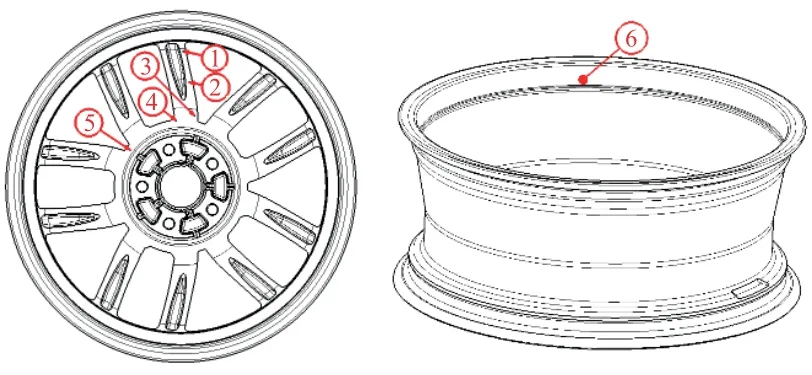
图6 应变测量点位置
根据图6 中所示的应力点集中可能位置,粘贴测量应变片。如图7 所示,为了研究测点位置平面应力的变化,本文采用0-45-90 应变花测量其平面应力,同时在应变片花的粘贴时,将0°,45°,90°位置应变片分布分别定义为水平方向、中间方向、垂直方向。

图7 试验车轮应变粘贴位置
其中水平方向的应变方向为平行于对应位置的轮廓线方向,如1 号应变花的水平方向为平行于轮辐的长度方向,垂直方向为垂直于轮辐长度方向;4号及5 号应变花水平方向为平行于对应位置的倒角方向;6 号应变花的水平方向为平行于车轮外缘,而对应的垂直方向为平行于车轮的轴线方向。由于试验过程中车轮产生温度变化较小,为简化试验过程,试验中采用四分之一桥路的形式。
4.1 径向疲劳台架测量与分析
车轮的径向疲劳中车轮应力测量如图8 所示,试验时直接将车轮应变连接到imc 采集器上,并通过计算机控制数据采集参数。试验时通过转鼓给车轮加载径向载荷。在进行车轮径向疲劳试验过程中,文献中对车轮旋转速度并没有进行特殊规定,为了减少车轮动态响应对测试结果的影响,试验时只考虑车轮准静态滚动过程中车轮载荷变化,车轮速度设置为1 km/h。

图8 径向疲劳台架试验
限于篇幅,文中只对几个典型位置的应变变化规律进行展示,首先对比了1,6 两个测点之间的水平方向和垂直方向的应变随车轮转角的变化过程。如图9 所示,C 曲线表示车轮顺时针旋转,A 曲线表示车轮逆时针旋转。同时可以看出在车轮准静态滚动过程中,测点1 位置出现了两个应变变化峰峰值,这两个峰值正好相差180°。这是由于最大峰峰值对应轮胎与转鼓接触的位置,而另外一个峰值是由于,当测点位置位于轮胎与地面接触位置正对面的位置时,由于轮胎的接触挤压使得轮胎与胎圈位置的压力增大,从而使得车轮辐条位置的受力增大。可以看出测点1 位置的水平方向和垂直方向的应力幅值的变化中出现了较大的峰值。正反方向的载荷变化规律基本相同,但峰值大小的变化主要是由轮胎的非线性导致的。同时可以看出第1 个测点的水平方向的峰值要比垂直方向大。从相位可以看出水平方向相位与垂直方向相位变化相差180°。如图10所示,测点6 的应变变化过程基本与测点1 相同,但是最大峰值变化较快,表明在车轮滚动过程中,轮胎与地面接触时,从测点6 位置所承受的载荷迅速变化。测点6 垂直方向的载荷变化可以看出,车轮正反方向旋转时应变存在一定的差异,水平方向应变值要比垂直方向大了10倍。

图9 测点1 位置应变变化历程
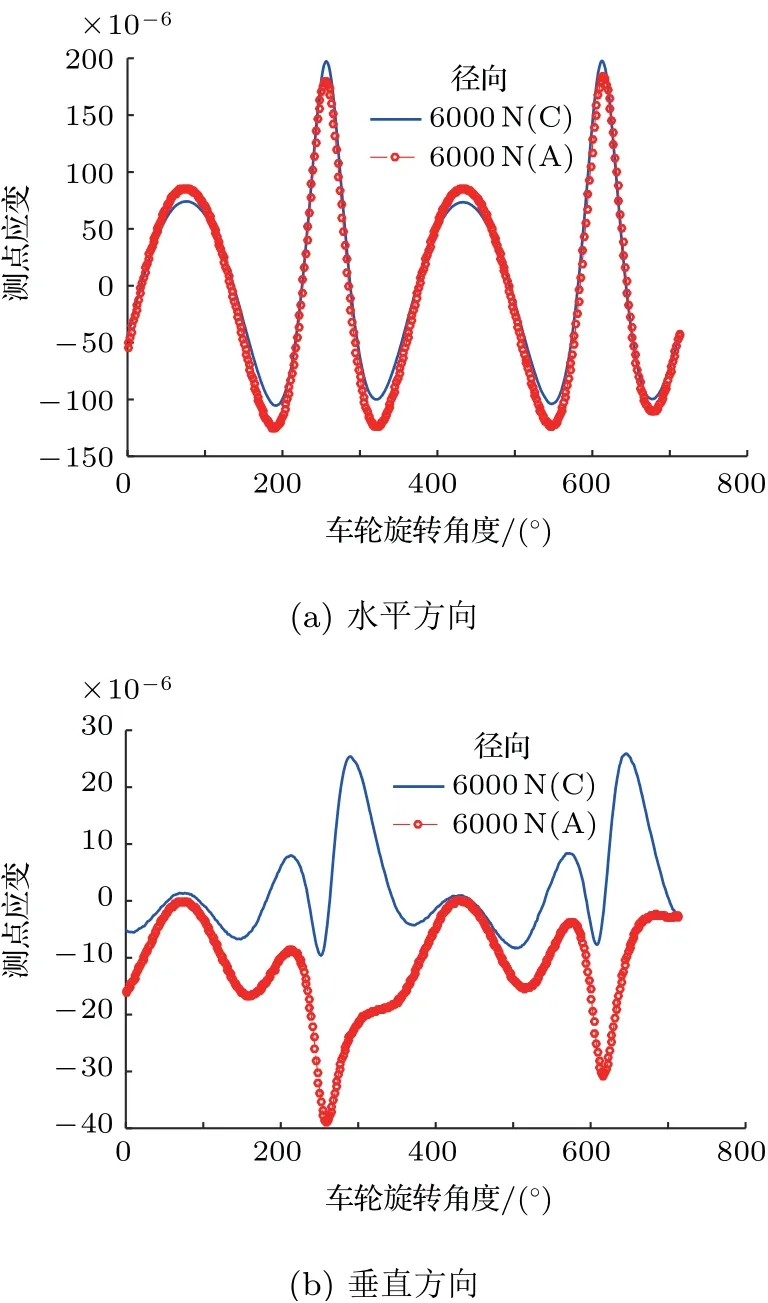
图10 测点6 位置应力变化历程
对比测点1和测点6可以看出,在径向载荷试验时,车轮的轮辋所承受的载荷最大,其中水平方向的载荷相对垂直方向具有绝对优势。同时轮辐上水平方向也有较大的载荷变化。越靠近轮心位置的载荷变化较小。
4.2 弯曲疲劳台架测量与分析
车轮弯曲疲劳试验中的车轮应力测量如图11所示,试验时将车轮应变直接连接到imc 采集器上,并通过计算机控制数据采集参数。试验时通过弯曲疲劳试验机给车轮加载弯曲载荷。此弯曲疲劳试验机原理是通过控制离心力产生弯矩,而离心力的大小是通过偏心质量大小以及旋转速度来定义。试验过程中分为5个恒定径向载荷加载,为了试验操作方便性,不同载荷加载时只改变离心质量的旋转速度。

图11 车轮弯曲疲劳台架测试流程
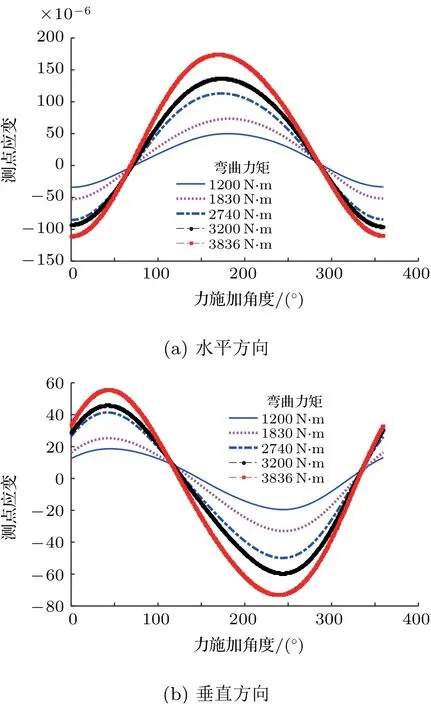
图12 测点1 位置应变变化历程
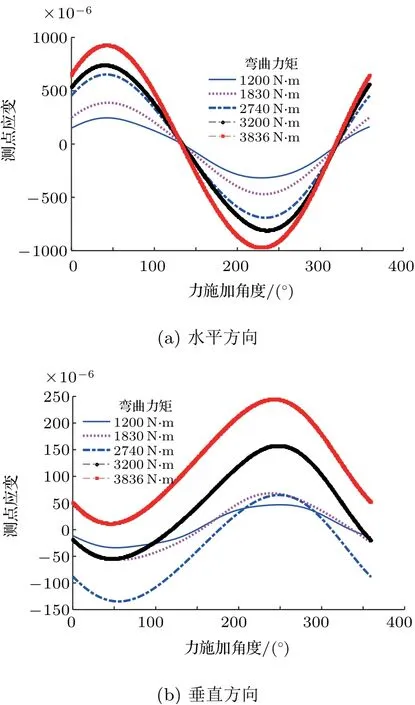
图13 测点4 位置应力变化历程
通过以上分析可以看出,在车轮的弯曲疲劳试验中,车轮轮辐沿长度方向并且靠近车轮轮心位置的点会出现较大的交变应力应变,同时也会对轮辋轴向方向产生较大的应力应变。
5 结束语
本文从车轮具体使用工况出发,分析了车轮可靠性的两种典型使用工况,基于此建立车轮可靠性台架试验时应力状态测试和分析方法。利用有限元仿真与试验相结合的方法,分析车轮径向疲劳试验和弯曲疲劳试验过程中,车轮的应力状态变化规律,可以得出以下结论:
(1) 车轮径向疲劳试验时,轮胎会对车轮的载荷产生较大的影响,轮胎与转鼓的挤压变形以及正反转动都会对车轮的应力状态产生影响。
(2) 车轮的径向疲劳试验时,车轮的最大载荷出现在轮辋与轮胎接触位置沿车轮圆周方向,而在靠近轮心位置的载荷较小。
(3) 车轮弯曲疲劳试验时,车轮的最大载荷出现在轮辐靠近轮心的位置,最大应变为沿轮辐的长度方向。
(4) 不同的载荷对车轮应变的变化规律并没有影响,但是会对最大和最小峰值产生影响。
