一类特殊连图的Tutte多项式

（辽宁师范大学 数学学院，辽宁 大连 116029）

1 引言及预备知识

图论中有许多值得研究的问题，其中关于图的等价分类问题就是图理论中的重要问题之一.图的不变量[1-7]是研究图等价分类的重要方法.图多项式是常见的图不变量，在空间图理论中具有十分重要的作用和地位.在图多项式中，Tutte 多项式是重要的多项式，另外Tutte 多项式也可以与Chromatic 多项式[8-9]紧密联系起来.

给定2个图G,H，u1,v1是图G的任意2个顶点，u2,v2是图H的任意2个顶点，将顶点u1,u2是用一条边连接起来，v1,v2是用n条边连接起来（见图1），所得到的图记作(1,n)，n≥ 1.

图1 图(1,n)

本文通过减边缩边定义，推导出来图(1,n)的Tutte 多项式计算公式.

T(G;x,y)通常也简记为T(G)或TG.

定义2[11]Tutte 多项式的减边缩边定义：（1）给定一个图G，G′和G′分别表示在图G中删掉一条边e和沿着边e收缩到一点的图，且边e既不是环边也不是割边，则T(G)=T(G′) +T(G′)；（2）假设图G是由i个环边和l个割边组成的，则T(G)=xi yl.

定义3[12]令图θn表示由2个顶点和n条连接这2个顶点的边构成的图（见图2），也称为s-theta 图.

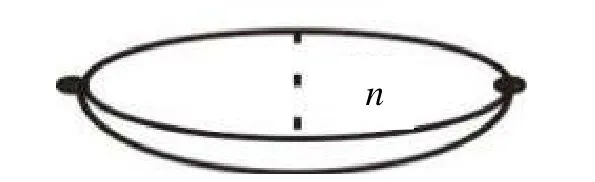
图2 图 nθ

给定图G1，G2，G1UG2表示图G1和G2的不交并，G1∨G2表示图G1和G2的一点并.

性质1[10]395若e为图G中的一条边，那么

2 主要结果及证明

定理对于图(1,n)，n≥ 1，有

其中：TG,TH分别为图G,H的Tutte 多项式；T(G:H)为图G,H的两点并的Tutte 多项式.

证明对图(1,n)的n条边中的一条边进行减边缩边的运算，再对n-1条边进行缩边减边的运算，以此类推，那么有等式

成立，其中：图Hn1-，Fn1-，En1-见图3.

图3 图H n1-，Fn1-，En1-

由式（2）可知

推论图θn的Tutte 多项式为.

证明根据定理和Tutte 多形式的定义，有

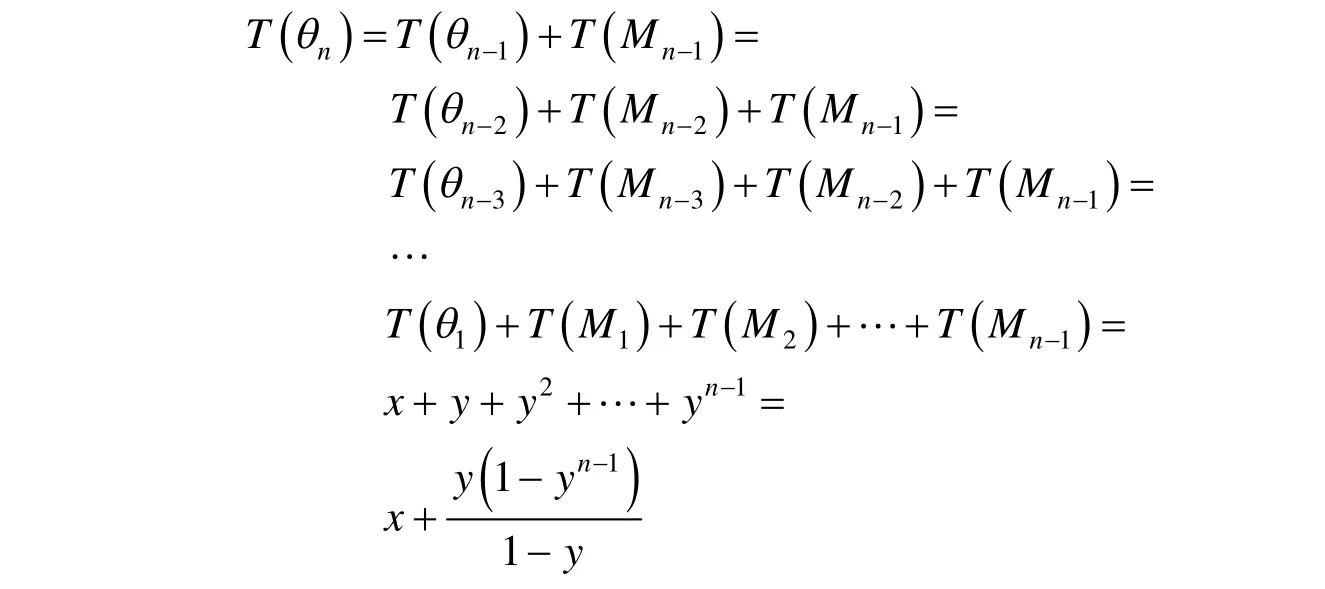
其中：图M i(i=1,2,L,n)为一个点连接i条环边所构成的图，且T(Mn)=yn，T(θ1)=x. 证毕.

3 结语

本文主要研究了一类特殊连图的Tutte 多项式，目前仅有扇图、轮图和Flower 图计算出了Tutte 多项式的具体表达方式.未来还可以研究其它更多图的Tutte 多项式的性质以及进一步探究Yamada 多项式与Tutte 多项式之间的联系.