基于DBSCAN的时序数据异常检测阈值选择算法研究

刘峰麟，殷铭，袁平

（1.四川大学计算机学院，成都 610065；2.东华大学信息科学与技术学院，上海 201620；3.重庆第二师范学院数学与信息工程学院，重庆 400067)

0 引言

异常检测是从一个数据集合当中检测出和推断的预期值不一致的数据元素，这些和预期值不吻合的数据元素，就被称为异常。异常检测广泛应用于信用卡欺诈检测、网络的入侵检测等多个领域中[1]。随着互联网的高速发展，以及微服务的大规模实践，庞大的后台系统每天产生大量的时序数据。从大量的时序数据中准确检测出异常，及时触发报警、排出故障对于保证互联网服务的高可用有重大意义。异常检测作为工业界服务器后台智能运维的重要组成部分，在各大公司都有着广泛应用。通过统计后台机器的关键指标信息构成时序数据，进行异常检测，可以极大降低运维成本。例如，腾讯有自研的Metis，采用统计、无监督、监督的方式对内部应用指标进行异常检测，以降低运维成本；推特、雅虎、领英等知名互联网公司都开源有自己的异常检测工具。

异常从类型上可以分为三类：点异常、上下文异常、集合异常[1]。如果单个数据相对于其余数据可以被认为是异常的，则该数据被称作点异常。如果数据在特定上下文中是异常的，但是在其他情况下不是异常，则该数据被称为上下文异常。如果数据所在的集合和该集合同处于一个数据集的其他兄弟集合不一致，则称该集合为集合异常。时序数据的异常检测有基于插件的方法和基于分解的方法[2]。基于插件的方法是根据历史时序数据集合，通过时序预测算法，得到未来一段时间的时序数据，若对于i时刻，存在，则认为i时刻存在异常，反之则正常。基于插件是指把经典的时序数据预测算法作为插件，嵌入到异常检测算法中。基于分解的方法是对时序数据进行分解，提取周期、趋势、季节性、自相关、非线性、偏态、峰度、林中小丘、李亚普诺夫指数等特征，通过检测噪声成分，如果噪声分量，则认为是异常，反之则正常。在时序数据的异常检测中，Nikolay等人[2]采用3σ准则，假定数据的分布服从正态分布。在正态分布的数据中，σ表示标准差，μ表示均值，3σ准则认为 99.7%的数据都在（μ-3σ,μ+3σ）区间内。然而，在数据不是正太分布的情况下，无法选出正确阈值。Zhao[3]提出枚举所有的阈值，并采用F-score作为度量来避免阈值选择问题。枚举阈值的方式会带来大量的计算，增加异常检测的时间延迟，回避了阈值选择的问题。为了解决上述问题，本文利用EWMA算法对时序数据进行预测建模，然后利用衡量预测精度的指标建立误差模型，提出了一个基于DBSCAN的时序数据异常检测阈值选择算法来对每个指标选择阈值，从而检测时序数据的异常，提高准确率。

1 算法实现

1.1 时序模型

建立时序模型是指对后台系统关键指标信息采集的数据进行建模，得到关键指标数据的观测时序数据模型和预测时序数据模型。时序模型建立的流程如图1所示。关键指标数据主要包括服务器运行时的CPU、I/O等数据，通过监控任务进行定时采集可以得到关键指标的书序数据。时序数据通过提前部署到服务器的程序进行采集，因而一般有着固定时间间隔。通常时序数据是完整的，但在个别情况下时序数据会出现数据丢失的情况。建立时序模型首先通过多个数据点提取原始时序数据的采样间隔时间，其中i是数据点的逻辑索引。若>interval，则进行线性差值，插入序列到点i和i+1之间，插值后的到完整的观测序列。经典的时序预测算法有MA（Moving Average）、HW（Holt Winter）等，MA（Moving Average）是通过创建数据集的不同子集的平均数来分析数据点的技术。MA也是一种卷积，过滤掉了时间序列中的高频扰动，保留有用的低频趋势。MA通常与时间序列数据一起使用，以平滑短期波动，突出长期趋势或周期。MA的衍生改进算法版本有SMA、WMA等。EWMA（Exponentially Weighted Moving Average）又称作EMA（Exponential Moving Average）是采用指数衰减加权因子的一阶无限冲激响应滤波器。对于时序数据的EWMA序列可以表示

其中，系数α表示权重降低的程度，是介于0和1之间的常数平滑因子。根据线性插值补全数据得到完整的观测时序数据模型和预测时序数据，可以建立误差模型。误差模型的度量指标由计算预测精度的三个主要指标构成，它们分别是：MAE（Mean Absolute Error）、MAPE（Mean Absolute Percentage Error）、MASE（Mean Absolute Scaled Error）。对于有：

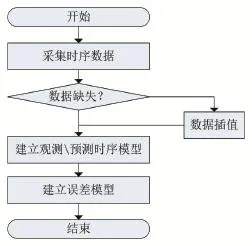
图1 时序模型建立流程图

1.2 基于DBSCAN的阈值选择算法

DBSCAN是经典的聚类算法，它依靠数据点间定义的密度度量来聚类。它通过指定数据聚类最小点数MinPts，和聚类距离半径ε自动依据数据点的密度聚类。相对于我们熟悉的K-means算法，不需要指定聚类的个数。聚类是一种无监督学习，它在样本没有标记的情况可以把数据分成不同的组，聚类算法分组的依据是数据间的距离度量值。在本算法中，采用最常见的欧氏距离作为DBSCAN的距离度量算法。

阈值选择对于时序数据异常检测来说至关重要。异常就是超过了一定阈值的数据，而阈值选择是一个复杂的问题，涉及到数据上下文等多个方面，好的阈值可以更准确地区分出正常和异常。误差模型中的阈值选择可以看做是另一个数据序列的异常检测问题。阈值选择不准确的一个原因是阈值数据中存在噪点。从这个角度出发，在没有样本标记的误差模型数据中，运用聚类算法剔除噪点，有助于选择更加合适的阈值。本文提出的阈值选择算法通过DBSCAN聚类算法在误差模型中发现噪点数据序列。对每个一个误差度量指标剔除掉噪点后得到修正误差模型k=1,2,3。然后，对修正误差模型中的每一个误差度量指标计算对应的误差阈值thk：

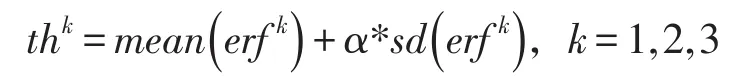
其中，mean是均值函数，sd是标准差函数，α调谐系数。接下来，对数据点用投票机制进行异常检测，如果一个数据点的多个误差度量指标中过半数的误差度量指标超过修正误差模型中对应的阈值，则该数据点视为异常。经过三个误差度量指标构成的投票机制，超过半数以上的度量指标判定该数据点异常的话，则最终认定该数据点是一个异常数据点，如上述，最终得到的时序数据异常检测的异常点结果可以用集合表示为

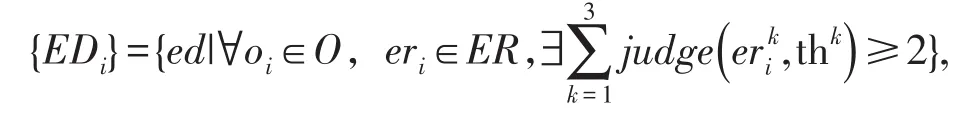
综上，基于DBSCAN的阈值选择算法的时序数据异常检测过程描述如下:

2 实验结果与分析

本文的异常检测实验依托于雅虎EGADS异常检测框架，在EGADS框架的基础上进行二次开发，实现该阈值选择算法。EGADS是一个良好的异常检测开源平台，它实现了基础数据处理、时序建模以及常见异常检测算法，开发者只需要对框架定义好的接口实现自己的算法即可得到异常检测的文本和图像结果，这有助于算法的分析和实践。

2.1 数据集

实验运用的时序数据是后台服务器的运行情况数据，该数据以（timestamp,value）形式存储。timestamp是以秒为单位的Unix时间戳，value是用小数表示的服务器CPU使用情况。实验数据通过后台工程师进行过异常标注，并且从工程实践的角度进行了重新讨论和审校，增加了部分异常点。

2.2 实验结果

在工程实践过程中，异常点的报警有助于运维人员及时根据异常点修复邻近时间窗口的异常。因此结合实际需要，在统计检测结果时，如果异常点所在的相邻几个时间窗口在存在真实异常，则表示异常召回成功。经过实验，对CPU使用情况数据的异常检测召回率、准确率、假阴性率结果如表1所示。

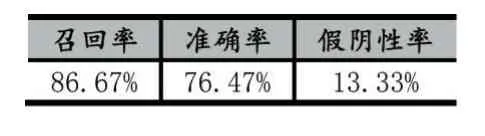
表1

3 程序运行界面效果

该程序运行的界面效果如图2所示，图中红色曲线是根据观测数据进行数据补全后建立的观测时序数据数据模型绘制出的观测时序图，横坐标是时间，纵坐标是观测值。图中蓝色曲线是根据经典的时序预测算法，在完整的时序观测数据基础上建立的预测时序数据模型绘制出的预测时序图，横坐标是时间，纵坐标是预测值。观测时序图中的黑色竖线是根据基于DBSCAN的时序数据异常检测阈值选择算法筛选的阈值，以投票机制对数据点误差统计度量进行筛检测到的数据异常点。

图2 时序数据异常检测程序界面

4 结语

本文总结了时序数据异常检测领域的有关文献，阐述了该领域的研究和应用现状。针对时序数据异常检测的阈值选择问题，提出了基于DBSCAN的时序数据异常检测阈值选择算法，该算法从阈值选择角度优化了时序数据异常检测的效果，具有实际工程价值。实验部分基于EGADS进行二次开发，在一个后台服务器运行数据上进行了测试，效果较好。

时序数据的异常检测是当下智能运维的重要组成部分[4]。今后还可以从以下几个方面深入，一，在时序数据建模上充分考虑周期性、季节性等特征；二，该算法检测异常的时间窗口较大，在时序预测和误差度量模型上改进，减小时间窗口；三，时序数据聚类效果好坏的一个关键因素是选择的距离度量算法是否能很好地适应时序数据的特征，考虑改进简单的欧氏距离度量算法，获得更适应时序数据特征的距离度量算法；四，在时序数据异常检测过程当中引入深度学习，进一步优化传统算法的效果。