基于销售网络的商品社团发现

丁云平

（四川大学计算机学院，成都610065）

0 引言

信息网络(Information Network)是 Jiawei Han、Philip S.Yu等在EDBT 2009和SIGMOD 2010的Tutorial上正式提出和倡导的新研究方向，是对现实空间中海量、多维、复杂结构数据和问题更具一般性的抽象[1，2]。近年来，信息网络的研究被广泛应用于通信网络、社交网络、生物网络等。

销售信息网络作为信息网络的一种，将商品的销售关系用网络图的形式进行表示，每个商品节点有销售量等属性，连接节点的边表示商品的共售关系。通过对销售信息进行网络建模，用户能够从多角度、多层次的观察和分析基于图的复杂主题对象，从而实时、直观地发现商品的销售情况，制定相应的销售策略。如图1所示。

图1 由传统销售项目集到新一代基于信息网络的销售网络

社团结构是信息网络的一个重要特性，在信息网络研究中是一热点问题[3-5]。社团结构是指网络中的顶点可以分成组，组内节点连接比较稠密，而组间顶点连接比较稀疏。由于社团结构广泛地存在于实际网络当中，是网络的重要性质，因此对社团结构的研究是了解网络结构和功能的重要途径。近年来关于社团的研究和相关的算法很多，但是这些研究仅考虑了网络本身的拓扑结构，并不考虑现实世界中的网络具有的显式或隐式信息，不适用于销售信息网络的研究。

1 相关概念与定义

为了更好的描述本文提出的算法，本节首先对相关概念进行数学定义。

定义1销售信息网络在无向图G=(V,E,W,N)中，V和E分别表示节点集和边集，W为边的权重，表示与之相连的两个商品节点共售的次数，N为节点的属性，表示节点的销量。表示节点的数量，表示边的数量。

定义2节点v的邻居对于给定节点v，其邻居节点集合NG(v)={u:(u,v)∈E}，dG(v)表示节点v的度。

定义3相关系数为了判断两个商品的相关性，引入相关系数（corru,v）这一概念，通过该参数来度量商品u，v的相关性：

其取值范围若为（1，+∞），则 u，v正相关，若为 1，则 u，v相互独立，若为[0，1）则 u，v负相关。

定义4杰卡德距离给定无向图G=(V,E,W,N)，节点u,v的杰卡德距离定义为：

考虑节点的相关性，初始的杰卡德距离为：

2 基于相关性的社团发现算法

传统的社团发现只考虑网络的拓扑结构，即同一个社团内部节点尽可能紧密、不同社团的节点之间尽可能稀疏，这种思想不能很好地反映现实世界的真实现象。例如，商品ABCDE只要有一次被购买，两两之间就会存在一条边，但真实情况是ABCD经常被一起购买，E只有一次和它们一起购买，如果采用传统的社团发现算法，只考虑网络的拓扑结构，挖掘出来的社团很可能是ABCDE，这与真实情况相悖，本文通过分析商品节点间的相关性解决这个问题。

为了解决传统社团发现算法中存在的弊端，在本节中，本文在文献[6]的基础上，引入销售信息网络自身的信息，提出了基于节点相关性的距离动力学社团发现算法。销售信息网络的每条边与初始距离d相关联，该距离受到两种交互模型和自身信息的影响，距离d动态地变化，增大或者减少，最后距离收敛（距离为1或者0）。最后移除距离为1的链接，销售信息网络将会被划分成若干不同的商品社团。

销售信息网络的每个节点，与其邻居在交互过程中，不同的邻居会对其产生不同的影响。设e={u,v}∈E是节点u和v之间的一条连边，由于网络拓扑结构和节点自身信息的作用，会有两种不同的情况会影响两个节点之间的距离d(u,v)。（1）直接影响；（2）间接影响。

（1）直接影响

节点u和节点v之间的距离d(u,v)明显地受到两个直接连接节点u和v的影响，但不同于社交网络，直接邻居的影响是积极的。在销售信息网络中，直接邻居的影响可能是消极的。本文通过节点之间的相关性描述两个节点之间的影响是积极的还是消极的。如果两个节点是负相关的，那么它们之间的距离直接为1（1为两个节点的最大距离），如果两个节点是正相关的，那么直接连接会导致距离d(u,v)的减小，公式如下:

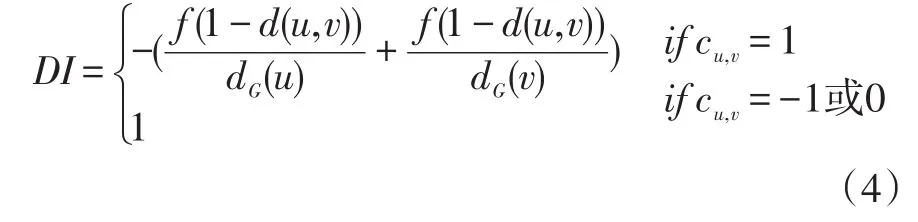
其中分母dG(.)为节点的度，f(.)是一个耦合函数（本文采用sin），1-d(u,v))表示u和v之间的关联度，两个节点之间的关联度越高，他们之间的影响越大。是归一化因子，用于考虑不同的连接节点之间的不同影响，即与度较小的商品节点相比，具有较大度的商品节点更难受到影响。

（2）间接影响

两个商品节点间的距离同样会受到其邻居的影响，为了定义邻居对距离的正面或负面影响，本文提出了一种基于相关性的启发式策略，基本思想是分析邻居节点x与u，v的相关性。如果邻居和节点u，v都是正相关的，则该邻居会吸引两个节点靠近，从而使距离减小，如果邻居和其中一个是负相关的，另外一个是正相关的，则会导致两个节点之间的距离增大，如果和其中两个节点都是负相关的，则认为该邻居会使两个节点的距离减小。如果邻居节点和其中一个或两个是不相关的，则认为该邻居节点不会对其距离产生影响，公式如下：

这里采用的归一化因子不同于公式（1），表示共售比重大的邻居对节点的影响更大。

最后距离动态变化公式为：

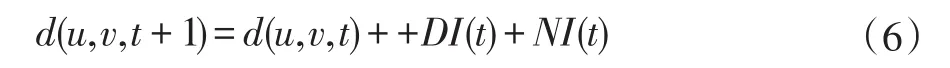
算法伪代码如算法1所示：

3 实验分析

3.1 实验数据

在这个实验中，一共使用了四个数据集。包括真实数据集amazon0302、chess和mushroom，以及IBM模拟数据生成器生成的模拟数据集T40110D100K。

表1 实验数据集相关统计信息

4组不同数据集节点度的分布情况如图1所示。

3.2 实验结果与分析

为了证明CCD算法的有效性，与文献[6]提出的算法Attractor进行对比，该算法在设计上只考虑网络的拓扑结构。实验结果如图2所示，从图中可以看出，本文提出的算法在四个数据集上均具有良好的表现，且在数据较大时，本文提出的算法在运行时间上更具优势。这是因为本文提出的算法在考虑商品节点相关性后，可以加快距离的收敛，从而减少算法运行时间。

图1 4组数据节点度分布

图2 运行时间

4 结语

本文提出基于相关性的距离动态社团发现算法，用于发现销售信息网络中更符合一般经验的商品社团。在两种距离交互模型的影响下，考虑商品节点之间的相关性，节点间的距离逐渐收敛为0或1，通过移除距离为1的边，从而动态地划分商品社团。相比于原始的Attractor算法，本文的算法能够较快地使网络之间的距离收敛，从而减少算法的运行时间，实验结果显示该算法具有较好的有效性。下一步将主要研究如何如何衡量发现的商品社团的好坏。