基于二元Copula函数的短期金融市场间相关性研究——以沪深股市为例

张钟元， 姜玥宏

( 辽宁石油化工大学 理学院， 辽宁 抚顺 113001)

随着国际经济形势的不断变化和国内产业结构的调整，金融市场短期内出现较大幅度的波动。作为金融市场的重要组成部分，股票市场是经济的晴雨表，直观反馈金融市场环境变化。股票市场间具有联动的相关性[1]，探讨金融市场相关性对于分析政策效果、风险防范、投资预测等具有重要意义。2008年金融危机美股大跌45%，市场失望情绪向其他国家股市蔓延并席卷全球。投资者对资本市场的判断直接影响他们在其他股市的投资行为，波动由一个资本市场向其他资本市场扩散，这种“溢出效应”[2]对于同一地区的股票市场影响更大。

“Copula”原意为“连接、交换”。Copula函数主要用于描述随机变量间的相关性，通过随机变量的边缘分布确定联合分布。由于选择边缘分布不受限制，在金融模型构建中更加方便。本文首先梳理金融市场的Copula理论研究现状，然后介绍使用的模型与方法，选取近年来波动幅度最大的2015年沪深股市数据进行数据处理和统计分析，经过整体性检验后估计典型Copula函数的参数，研究沪深股市指数日收益率的相关性后选出最优的Copula函数，经检验得出结论及相关经济解释。

一、文献综述

随着现代金融研究中统计建模方法的快速发展，国外学者首先将Copula函数引入金融领域，并逐步成为金融领域相关性分析和多元统计分析的一种重要工具。Copula理论在金融领域发展的时间较短，最早可以追溯到1959年，Sklar提出一个Copula函数用于描述变量间相关性。Nelsen进一步明晰了Copula函数的定义，同时介绍阿基米德Copula函数及其相关性[3]。Embrechts将Copula函数理论应用到金融学领域，针对相关性度量方法及线性相关指标局限性进行深入探讨。Bouye等人在金融数量分析中使用Copula函数，拓展其在金融领域的应用[4]。其后众多学者进一步研究，使Copula函数在金融领域的应用逐步完善。Bedford和Cooke提出随机变量选取的可视化模型[5]，Chen研究了多变量相关关系[6]，Nikoloulopoulos和Joe等介绍了Copula函数的尾部相关性和非对称性在金融数据处理上的应用[7]，Hobak Haff阐述了Copula函数在金融领域的参数估计方法[8]。Copula函数在金融领域应用的广度和深度不断加强，取得了一系列成果。

我国受资本市场发展限制，对Copula函数的研究起步较晚，但也取得了丰富的研究成果。张尧庭首次在国内介绍了Copula函数概念、性质，并分析其在股市风险分析中的作用[9]。金融波动和危机的频繁出现后，韦艳华、张世英进行了上证指数和深证指数的相关性分析，证明Copula函数在股市相关性分析中的优越性与实用性[10]。孙志宾、顾岚对Copula函数分类后说明其在金融领域分析的有效性[11]。随着Copula函数的研究，史道济、姚庆祝介绍Kendall秩相关系数τ和Spearman秩相关系数ρ的计算方法，针对1995—2002年数据进行模拟验证[12]。Copula函数在金融领域应用渐渐成熟，在相关性验证、风险评价等方面取得较为丰富的研究成果。陈守东、胡铮洋使用Copula函数对1996—2004年数据进行模拟分析，度量证券市场的风险[13]。吴吉林、张二华使用2005—2009年的上证、恒生、日经、标准普尔 500建立Copula模型，计算相依结构判定次贷危机风险[14]。沈传河、王向荣针对2006—2013上证及深证指数数据，使用Clayton Copula函数研究货币与资本两个市场的联合分布变化情况[15]。马薇等人利用2009—2014年的深证和恒生数据测度风险相关性，发现2008年金融危机后Clayton-Gumbel Copula函数对两市拟合效果最好[16]。白雪、牛锋使用EVT-Copula方法的建模，对涵盖较多金融大事件的2007—2015年金融体系收益率数据拟合，进行风险测评[17]。

国内外Copula函数研究已经取得了较为丰硕的成果，特别在波动期的金融市场联动、风险评估等方面表现突出。但是，现有研究大多使用长期数据进行估计，缺乏针对短期数据的分析。长期数据更易满足模型限定条件保障模拟效果，然而短线投资者利用长期数据分析结果会忽略一些短期变化。我国正处于经济快速变化时期，国际经济政策和国内深化改革措施都会产生短期较大波动，有必要针对短期数据进行分析。

二、模型与方法

Copula函数是将联合分布函数与各自的边缘分布函数相连接的连接函数。在金融的相关分析中，大多用于金融市场间相关性研究，在已有的Copula函数中主要使用椭球类Copula函数和阿基米德Copula函数。

(一)Copula函数及检验

定义1二元Copula函数C(·,·)具有以下性质[18]：

(1)C(·,·)的定义域为：I2即[0,1]2；

(2)C(·,·)有零基面且是二维递增的；

(3)对任意变量u，v∈[0,1]满足：C(u,1)=u和C(1,v)=v。

基于常用二元Copula函数的相关性度量，主要使用Kendall秩相关系数τ和Spearman秩相关系数ρ。

(二)经典椭球类Copula函数定义及其相关性

椭球类Copula函数由椭球分布得到，多为对称函数，常用于金融分析包括正态Copula函数和t-Copula函数，其性质相对简单，模拟算法较为成熟。

1.二元正态Copula函数

二元正态Copula函数的分布函数、密度函数分别为：

(1)

(2)

(1)(2)式中，Φ(u)、Φ(v)为标准一元正态分布函数，Φ-1(u)Φ-1(v)为其逆函数，ρ∈(-1,1)为Φ-1(u)、Φ-1(v)的线性相关系数。

二元正态Copula函数是较为基础的Copula函数，具有对称的尾部，适用于尾部渐进独立的二维随机向量。由于二元正态Copula函数具有对称性，无法准确描述金融市场之间的非对称相关关系，实际中非对称情况更为普遍，因而受到数据限制，应用范围相对较窄。

2.二元t-Copula函数

二元t-Copula函数的分布函数、密度函数分别为[19]：

(3)

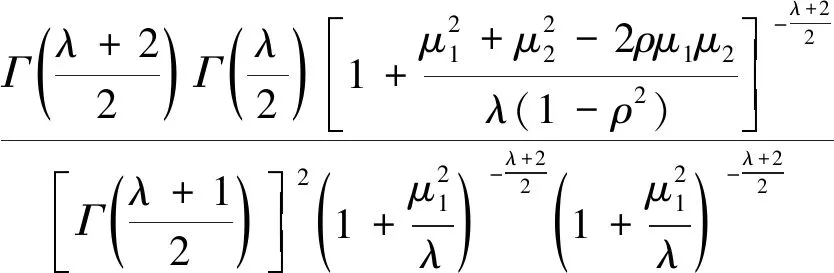
(4)

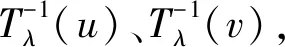
与二元正态Copula函数类似，对于市场之间对称的相关关系分析较好，二元t-Copula函数仍需要相依结构的正态假设。虽然极端值模拟仍然不够准确，但二元t-Copula函数具有较厚的尾部，对变量间尾部的变化更为敏感。在实际金融市场应用中，能够拟合具有尾部相关情形，适用程度更广。

(三)经典二元阿基米德Copula函数及性质

Copula族中应用最广泛的是阿基米德Copula函数，包括许多参数族，由不同的生成元构造，具有构造简单、分布特征各异的Copula函数，而且各个Copula函数的相依结构差异很大，易于区分。

定义2设φ:[0,1]→[0,∞]为连续、严格递减凸函数，φ(1)=0，则：

C(u,v)=φ[-1](φ(u)+φ(v))

(5)

如果φ(0)非∞而为有限值，φ[-1]定义为：

(5)式中，φ为阿基米德Copula函数的生成函数，且满足：

φ(u)+φ(v)≤φ(0)

对任意的0≤u,v≤1，有φ(1)=0，φ′(u)<0，φ″(u)>0。

阿基米德Copula函数在金融中应用广泛，较为典型的是Gumbel Copula函数、Clayton Copula函数、Frank Copula函数。

1.Gumbel Copula函数

Gumbel Copula函数的生成元、分布函数、密度函数分别为：

φ(t)=(-lnt)α,α≤1

(6)

CG(u,v,α)=

(7)

(8)

Gumbel Copula函数具有非对称性密度，其尾部上高下低，呈“J”字形，对变量分布上尾部的变化感知明显，适宜分析具有上尾相关特性的金融市场相关关系。因而在牛市时期，股票市场之间相关性增强，即一个股票市场股票价格暴涨会带动另一个股票市场股价上涨。因此该函数可以有效分析两个股票市场之间的相关性。

2.Clayton Copula函数

Clayton Copula函数的生成元、分布函数、密度函数分别为(9)(10)(11)式所示[20]：

(9)

(10)

cC(u,v;α)=(1+α)(uv)-α-1(u-α+

(11)

Clayton Copula函数具有非对称性密度，其尾部上低下高呈“L”形，函数具有对变量分布下尾部的变化感知明显的特点，分析下尾相关特性的金融市场之间相关关系具有独特优势。对于熊市时期股票市场之间的相关性增强情形拟合较好，即股票市场间形成价格跌幅的联动预期一致，两个股票市场之间存在较强的正相关性。

3.Frank Copula函数

Frank Copula函数的生成元、分布函数、密度函数分别为(12)(13)(14)所示[21]：

(12)

CF(u,v;α)=

(13)

cF(u,v;α)=

(14)

当α>0时，随机变量u、v正相关；当α→0时，随机变量u、v趋近于独立；当α<0时，随机变量u、v负相关。

Frank Copula函数具有对称性密度函数，具有对称的尾部，分布呈“U”字型，适合描述具有对称相关结构的金融市场之间相关关系。变量在分布的尾部具有渐进独立性，表现为对上尾部和下尾部相关性变化均不敏感，对金融市场中的尾部相关性变化感应度较低。

(四)经验Copula函数

在金融领域中需要评价模型优劣性，因此引入经验Copula的概念来评价模型模拟效果的优劣。

定义3设(xi,yi)(i=1,2,…,n)为取自二维总体(X,Y)的样本，记X、Y的经验分布函数为别为Fn(x)和Gn(x)，定义样本的经验Copula[22]如下：

u,v∈[0,1]

(15)

(15)式中，I[·]为示性函数，当Fn(xi)≤u时，I[Fn(xi)≤u]=1,否则I[Fn(xi)≤u]=0。

并使用平方欧氏距离进行判定：

(16)

(16)式中，ui=Fn(xi)，vi=Fn(yi)(i=1,2,…,n)。平方欧氏距离的计算结果越小，意味着模型的拟合效果越好。

三、实证分析

(一)数据的选取与处理

股市综合指数是考察股票市场的重要评定指标，是较为直观的观测指标，作为动态指标在统计计算中具有一定难度。因此在现有研究中，衡量股票市场中股票价格水平多采用股票指数，将日收益率作为统计指标[23]。本文研究主要针对短期数据的不确定变化，因此选择近几年年内伴有剧烈振幅的股市数据，经过筛选发现股市在2015年震荡幅度相对最大。由此，本文采集了2015年1月5日至2015年12月31日的上证和深证股票市场的开盘价、最高价、最低价、收盘价等共计488组数据，以此计算沪深股市的日收益率：

日收益率=(收盘价-开盘价)/开盘价

下文将使用沪、深两市日收益率数据，建立二元Copula函数模型分析两市相关性问题。本文数据来源于同花顺网站，模拟采用MATLAB软件编程计算。

(二)正态性检验

金融数据建模首先需要检验样本是否符合正态分布，本文运用SPSS软件得到样本的收益率序列的描述统计量和频率直方图,如表1、图1所示。

表1 日收益率序列的描述统计量

(a)深市日收益率

(b)沪市日收益率

从表1和图1(a)图1(b)可以看出沪深两市日收益率序列，都存在一定程度尖峰厚尾、非对称的特性，显然与正态分布存在差异。沪市日收益率序列偏度大于零，深市日收益率序列偏度小于零，两市日收益率序列都呈现高峰且具有比正态分布更厚的尾部。对沪深日收益率序列分别进行正态性检验，调用jbtest函数和lillirtest函数的检验结果，如表2所示。

表2 沪深股指的正态性检验

表2沪深股指的正态性检验中两种检验的h的值均为1，p的值均小于0.01，说明沪、深市的日收益率序列均不服从正态分布，而是服从某种对称的尖峰厚尾分布。调用ecdf和ksdensity函数，使用样条插值法和核密度估计法，得到的上证指数日收益率经验分布函数和核分布估计差别非常微小，从图像上看几乎一致；类似的，深证成指日收益率的经验分布函数和核分布估计差别同样微小，图形基本重合，具体如图2(a)(b)所示。因此，采用核分布函数作为总体的近似分布函数，重合度、可靠性较好。

(a)沪市日收益率

(b)深市日收益率

(三)Copula函数的选择

通过绘制二元频数分布直方图(见图3)观察联合密度函数的尾部特征，本文选用椭球类的t-Copula函数和阿基米德Copula函数中的Gumbel Copula、Clayton Copula和Frank Copula函数。这些函数分别具有尾部渐进独立性特征、中上尾特征、下尾特征以及对上下尾部都不敏感特征，较好地满足对尾部特征拟合的全面验证。对数据进行拟合后估计Copula函数的参数，使用密度函数图、最小欧式距离检验，最终筛选出拟合效果最好的Copula函数。

(a)频数直方图

(b)频率直方图

从沪深股市日收益率的边缘分布的二元直方图看，其不满足二元正态Copula函数基本条件，将其排除。利用MATLAB编程对剩余四种Copula函数计算，可以得出四种Copula函数中相应的参数值。具体结果如表3所示。

表3 沪深股指的四类Copula参数

使用Copula函数中估计出的参数，通过MATLAB软件绘制Copula函数的密度函数与分布函数图。将其与图3和图4对比，发现Clayton Copula与沪深股市的二元频数直方图上尾部图像不符，Frank Copula函数与沪深股市的二元频数直方图下尾部图像不符。因此，本文仅展示与二元频数直方图尾部特征基本吻合的t-Copula函数与Gumbel Copula函数，密度函数与分布函数图与二元频数分布直方图呈现如下(见图4、图5)。

2015年股市大起大落，其中沪市4月份、6月份、11月份、12月份上涨幅度在全年中较为显著，而深市在4月份、6月份以及11月份的上涨幅度尤为突出，通过以上图形可以看出，两股市之间在上尾部呈现很强的相关性。其中，Gumbel Copula函数拟合图像具有明显上尾特征，能更好地反映沪深股市日收益率之间尾部的相关性，拟合效果比t-Copula函数更好。

(a)密度函数图

(b)分布函数图

(a)密度函数图

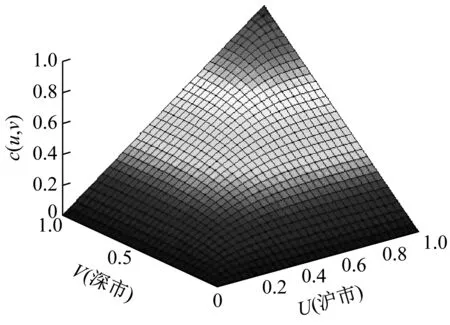
(b)分布函数图

分别计算t-Copula函数、Gumbel Copula函数、Clayton Copula函数和Frank Copula函数对应的Kendall秩相关系数τ和Spearman秩相关系数ρ，具体数值如表4所示。

表4 沪深股指四类Copula函数中的Kendall秩相关系数τ和Spearman秩相关系数ρ

表4中的数据对比结果发现Gumbel Copula的Kendall秩相关系数τ和Spearman秩相关系数ρ更接近直接观测原始数据。说明参数为αG=2.8659的Gumbel Copula反映沪深股市日收益率之间的相关性效果更佳。

(四)模型评价

为了评价两个模型优劣，建立经验Copula函数，对二元t-Copula函数和Gumbel Copula函数模型进行检验。两个函数的平方欧式距离公式如(17)(18)：

(17)

(18)

四、结论与展望

本文通过取自同花顺中2015年度沪深股市的488组数据，使用短期振荡幅度较大的股市数据进行Copula函数拟合，运用MATLAB软件进行数据编程计算，对经典Copula函数进行筛选，筛选出恰当的短期数据拟合函数。频率直方图显示沪深股市都呈现尖峰厚尾特点，对统计量进行分析后发现各个收益率序列不具有正态性，并使用相关性分析，估计出二元Copula、Gumbel Copula、Clayton Copula以及Frank Copula函数的参数值。实证分析中，2015年沪深股票市场日收益率的时间序列具有异常峰值，结果显示出样本波动的突发性和显著性；参数估计结果显示,沪深股市日收益率波动之间是强正相关关系，波动的运动趋势基本一致；模型拟合筛选通过正态性检验、相关系数检验以及经验函数检验，结果显示在几种常用Copula函数中Gumbel Copula函数可以更好地拟合沪深股市的日收益率序列。研究表明，沪深两市的股票收益率和市场波动性具有互动性和整合性，即当上证股市上涨时深成股市也随之上涨。因而本文研究可以有效地进行股市短期的相关性预测，预测结果既可以辅助投资者进行风险控制，同时也可以为政府宏观调整进行辅助分析，具有一定实际意义。

图6 经验Copula分布函数图

本文研究短期股票市场数据的相关性，扩大了Copula函数的应用范围，为投资者股票的投资组合决策提供了短期数据分析理论依据。研究选取了近几年股市波动幅度最大的一年数据进行实证分析，分析结果与前人对长期数据研究存在差异性。一方面，短周期数据不能完美地满足序列的对称性，数据中存在一些偏离性的特殊值，显示出股市日波动的显著性。另一方面，从拟合结果看，短期数据的Copula函数选取与长期数据也具有差异性，这对短期投资策略调整具有重要意义。因此，作为长期跟踪的辅助分析手段，短期数据Copula函数拟合分析对投资者实时调整投资策略具有一定实际意义。同时，对短周期股票市场数据进行相关性分析，减少了数据收集量，降低了Copula函数应用的原有门槛，使分析更具可操作性。而短期数据变动更为明显，对于市场反应更加迅速，有助于增加预测的时效性。随着中国经济改革深入，国内外经济环境也更为复杂，政策性调整和国际贸易形势将更加多变，而股市受政策影响容易出现较大幅度波动，这对投资者影响较大。基于本文研究结果，建议在投资者出现较大政策或经济形势波动时，在长期数据分析基础上，及时增加短期股票市场之间相关性的分析，考察股市间这种溢出效应。特别在长期数据难以获取或者受其他因素影响无法获取时，建议投资者及时采用短期数据Copula函数拟合进行预测，这将有助于在金融风险管理分析中度量风险，进而让投资者做出更为适当的决策。

本文研究了短期数据的Copula函数拟合问题，由于时间及能力的限制仍存在有待解决的问题。本文对二维数据拟合过程中使用较为成熟的椭圆Copula函数与部分单参数阿基米德Copula函数，对阿基米德Copula函数双参数、多参数及多维Copula函数并未涉及。现有Copula函数在金融领域应用前景比较好，但在具体计算机软件开发实现上存在一定困难，这也使Copula函数应用受限，随着这些问题的不断解决， Copula函数在未来金融领域中相关性问题研究中将更为有效。