HOPF BIFURCATION ANALYSIS IN A MONOD-HALDANE PREDATOR-PREY MODEL WITH THREE DELAYS∗

Renxiang Shi

(Dept. of Mathematics, Nanjing University of Chinese Medicine,Nanjing 210023, Jiangsu, PR China)

Abstract We analysis Hopf bifurcation in a Monod-Haldane predator-prey model with three delays in this paper. Fixing τ1 and τ2 and taking τ3 as parameter,the direction and stability of Hopf bifurcation are studied by using center manifold theorem and normal form. At last some simulations are given to support our results.

Keywords Hopf bifurcation;Monod-Haldane predator-prey model;delays

1 Introduction

The dynamics of predator-prey model with delay have attract many interest for researchers [1-8], For example [3,8] discussed the effect of delay on the global stability for predator-prey system,[6]discussed Hopf bifurcation of a ratio-dependent predator-prey system with two delays,besides[4]studied Hopf bifurcation of delayed predator-prey model with stage-structure for prey.

We know that Holling functional response is usually used to represent the grasping for predator and the functional responses is usually monotonic. But in microbial dynamics or chemical kinetics, the functional response represents the uptake of substance by the microorganisms,and the nonmonotonic responses occur by experiment.For example the inhibitory effect on the growth rate occurs when the nutrient concentration reaches a sufficient level[9]. This case always exists when micro-organisms are used for waste decomposition or for water purification [11]. The response functionis proposed by Ardrew to present the inhibitory effect which is called Monod-Haldane function [10] at hight concentration. Besides Sokol and

Howell [12] proposed a simple Monod-Haldane function of formto describe the uptake of phenol by a pure culture of Pseudomonas putida growing on phenol in a continuous culture. In [13] the ability of predator for prey is expressed by simplified Monod-Haldane functionSo we think Monod-Haldane function in predator-prey model should be more realistic in some situation. Besides the diffusion between patch is introduced into predator-prey model should be more reasonable. As we know, some kinds of delays always exist during the works about predator-prey system, such as the hunting delay for predator, the delay caused by gestation or maturation for predator and so on. Recently the following predator-prey system [21] with three delays was studied:

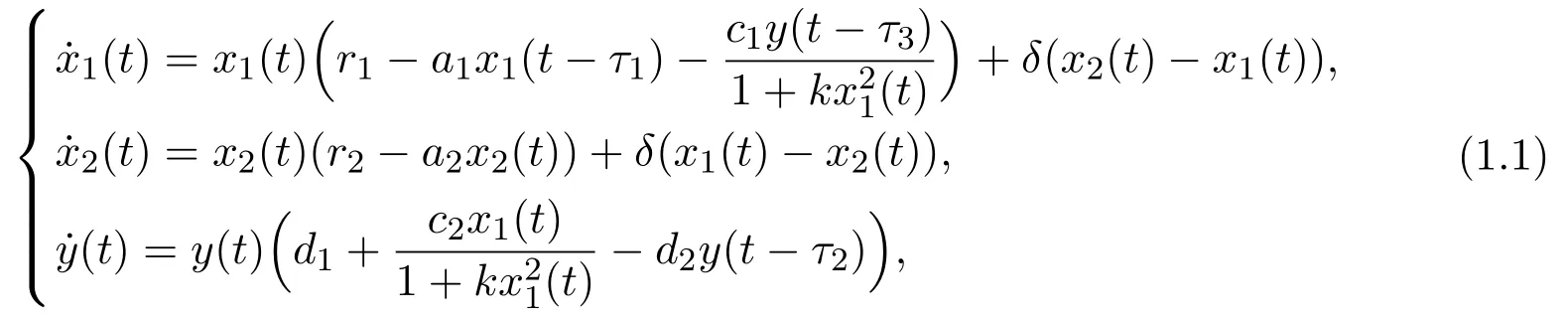
with the initial condition:

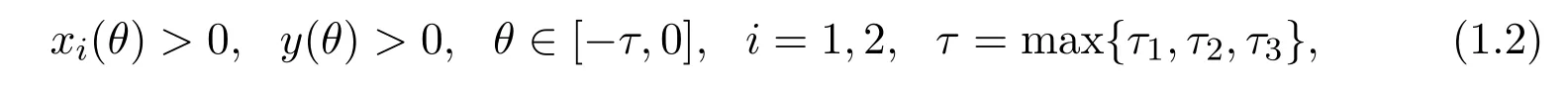
wherex1(t),x2(t)denote the numbers of prey species in patch 1 and patch 2 respectively,y(t)denotes the numbers of predator species in patch 1,c1is the capture rate.Monod-Haldane response functionexpresses the capture ability of predator,c2denotes the conversion rate,ri(i=1,2) is the birth rate of prey species in patchirespectively,ai(i= 1,2) andd2are the coefficients of intra-specific competition,d1is the birth rate for predator, the delaysτ1,τ2represent negative feedback of prey and predator in patch 1 respectively,τ3is the hunting delay.δis the diffusion coefficient.

Assumingτ3= 0, the author [2] studied the Hopf bifurcation of system (1.1)with two delays (τ1andτ2) under four cases: (1)τ1̸=0, τ2=0, (2)τ1=0, τ2̸=0,(3)τ1=τ2=τ ̸=0, (4)τ1̸=τ2, τ1∈(0,τ10), τ2>0. But delayτ3always exists in reality, we should consider its importance for dynamics. Although there are many works about Hopf bifurcation with two delays [6,14-17]. But in my opinion, the Hopf bifurcations with three delays[19,20]are rarely. In[20], the author considered the following model HIV-1 system with three delays:

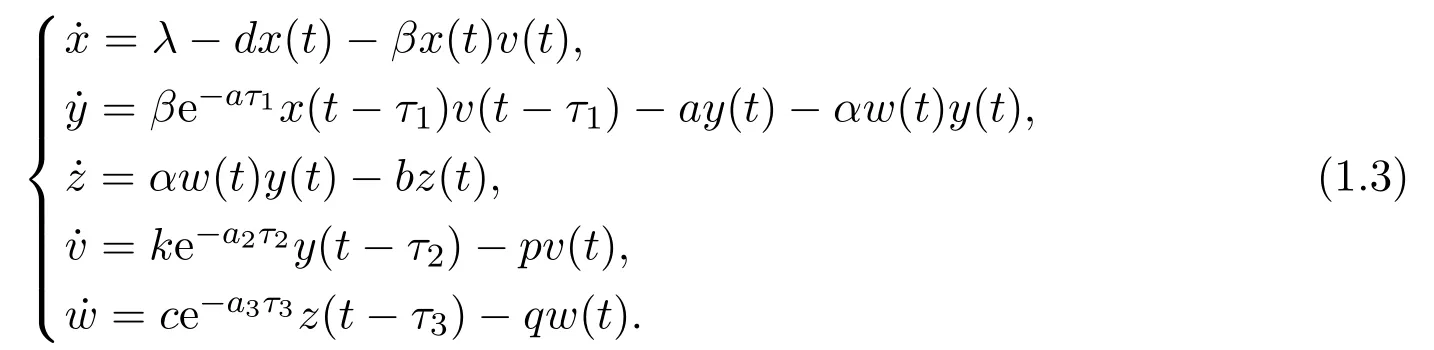
The dynamics were discussed under three cases: (1)τ1>0,τ2=τ3= 0, (2)τ1∈(0,τ10), τ2>0, τ3=0, (3)τ1∈(0,τ10), τ2∈(0,τ20), τ3>0.

Stimulated by above work, we should discuss the Hopf bifurcation of system(1.1) with three delays in this paper. In the first part, based on work [2], we give dynamics of system (1.1) under two cases: (1)τ1>0, τ2=τ3=0, (2)τ1∈(0,τ10),τ2>0, τ3= 0, then we discuss Hopf bifurcation of system (1.1) with three delays(τ1∈(0,τ10), τ2∈(0,τ2∗), τ3>0) and give the direction and stability of Hopf bifurcation by center manifold theorem and normal form[18], at last we should give simulation to support our results.

2 Preliminary Work

Before our discussion, we give the following result:

Theorem 2.1The solution of system(1.1)with initial(1.2)is positive.

ProofBy the fundamental theory of functional differential equation [22], system (1.1) with initial condition (1.2) has a unique solution (x1(t),x2(t),y(t)), t ∈(0,+∞).

Now we provex1(t)>0, t>0. Otherwise, there exists at∗∈(0,+∞),x1(t∗)=0. We definet1=inf{t:x1(t)=0}, from the first equation of (1.1) we get ˙x1(t1)=δx2(t1)<0, sox2(t1)<0. Definet2= inf{t:x2(t) = 0}, we knowt2< t1. From the second equation of (1.1), we get ˙x2(t2) =δx1(t2)<0, sox1(t2)<0, which is a contradiction.

Similarly, we provex2(t)>0,t>0. Suppose on the contrary that there exists at∗∈(0,+∞),x2(t∗)=0. We definet3=inf{t:x2(t)=0},from the second equation of (1.1) we get ˙x2(t3) =δx1(t3)<0, sox1(t3)<0. Definet4= inf{t:x1(t) = 0},we knowt4< t3. From the first equation of (1.1), we get ˙x1(t4) =δx2(t4)<0, sox2(t4)<0, which is a contradiction.

From the third equation of (1.1), we get

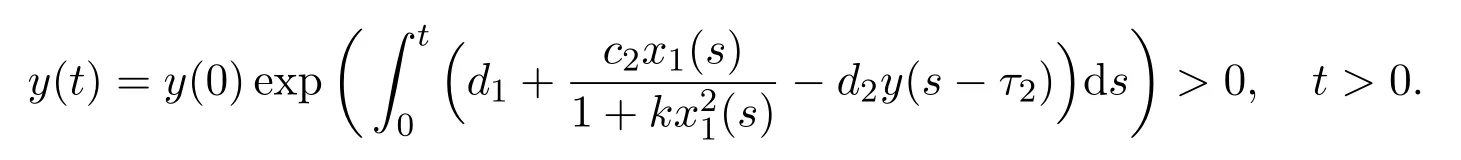
The solution is positive, which means that preys and predator always exist.

From [2], we know system (1.1) has at least a positive equilibriumwhere

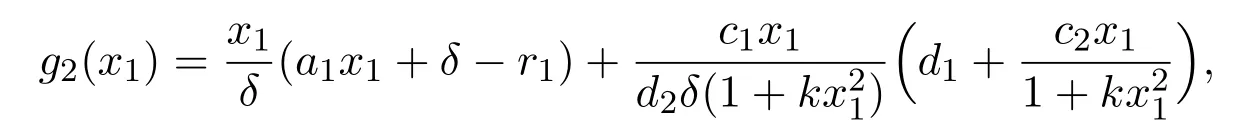
if the following hypothesis hold:

furthermore we have:

Lemma 2.1[2]The solutions of system(1.1)with initial condition(1.2)are ultimately bounded, that is, there exist positive constants M1,M2and T such that for t ≥T:

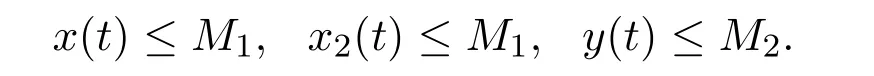
By transformationsystem (1.1) becomes

where

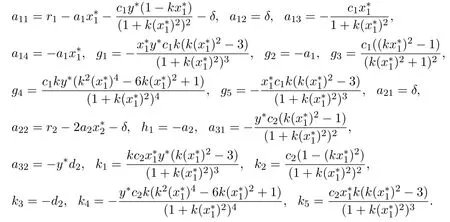
For system (1.1), the characteristic equation ofis

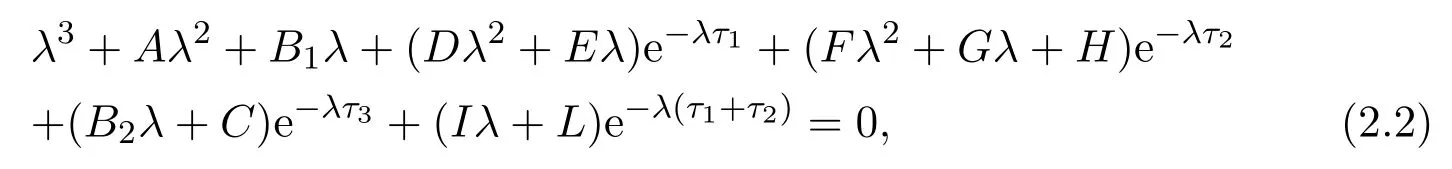
where

Whenτ3=0, denoteB=B1+B2, then equation (2.2) becomes

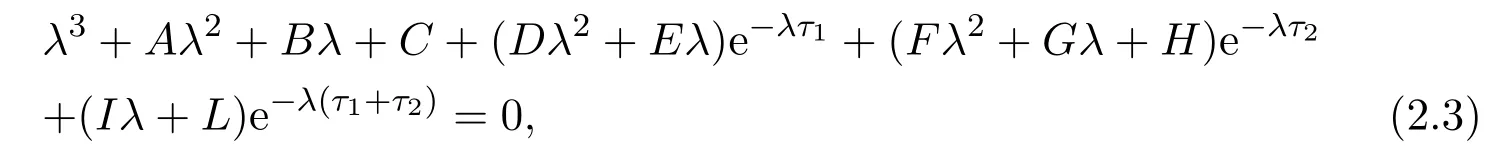
which is the the characteristic equation in [2]. The dynamics of system (1.1) is similar to [2], so whenτ1=τ2=τ3=0, equation (2.3) becomes

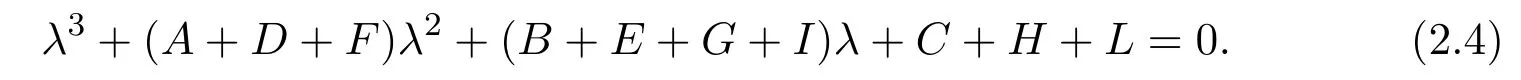
All the roots of equation (2.4) have negative real parts if and only if

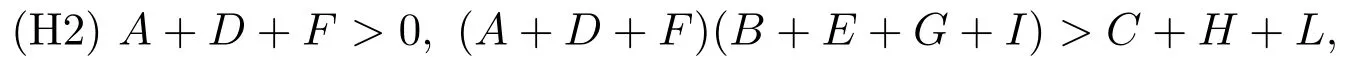
so the equilibrium pointof system(1.1)is locally asymptotically stable if (H2) holds.

whereA12=A+F, A11=B+G,A10=C+H,B12=D, B11=E+I, B10=L.

Lettingλ=iω(ω >0) be the root of equation (2.5), from the discussion in [2],we obtain

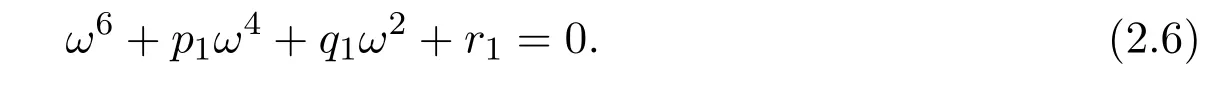
By denotingv=ω2, equation (2.6) becomes

Lemma 2.2[2]For the third degree exponential polynomial equation(2.5), we have the following conclusions

(i)When r1≥0andall roots of equation(2.5)have negativereal parts for all τ1≥0, thus the equilibrium pointof system(1.1)isasymptotically stable for τ1≥0.

(ii)If either r1<0or r1≥0,all hold, equation(2.7)has at least one positive root vk and all roots of equation(2.5)have negative real parts for τ1∈[0,τ10), then system(1.1)at the positive equilibriumpoint E∗is local asymptotically stable for τ1∈[0,τ10).

(iii)If all the conditions stated in(ii)and h′(vk)̸= 0are satisfied, then system(1.1)exhibits the Hopf bifurcation at the positive equilibrium point E∗for τ1=

The definitions ofr1,p1,could be founded in [2].

Case (2)τ1∈(0,τ10), τ2>0, τ3=0, we have:

Lemma 2.3[2]For system(1.1), suppose that(H4),(H5)in[2]hold, and τ1∈(0,τ10), then the positive equilibrium point E∗of system(1.1)is locally asymptotically stable for τ2∈[0,τ2∗)and system(1.1)at the positive equilibrium point E∗undergoes a Hopf bifurcation when τ2=τ2∗. That is, system(1.1)has a branch of periodic solutions bifurcating from the E∗near τ2=τ2∗.

The definitions of (H4),(H5) andτ2∗could be founded in [2].

3 Hopf Bifurcation about Three Delays

Whenτ1>0, τ2>0, τ3>0, we takeτ3as parameter,τ1andτ2in its stable interval, letiw(w >0) be a root of equation (2.2), we obtain

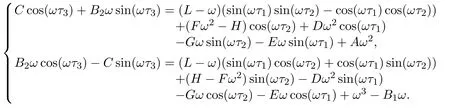
Eliminatingτ3, we obtain

where

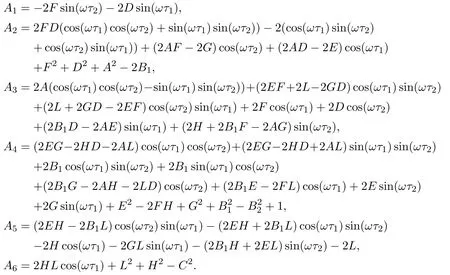
Denote

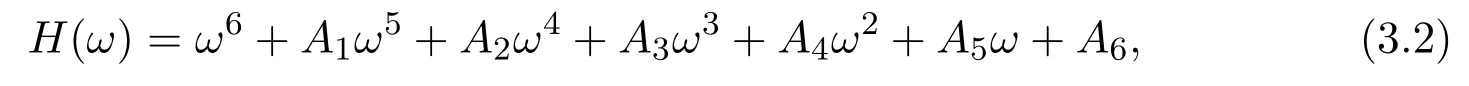
we then give the following hypothesis:

(H6) Equation (3.1) has finite positive roots.If (H6) holds, we denoteω1,ω2,··· ,ωkto be positive roots of equation (3.1).

For every fixedωi(i=1,2,··· ,k),then exists a sequence0,1,2,···}, whenτ1∈(0,τ10),τ2∈(0,τ2∗),

where

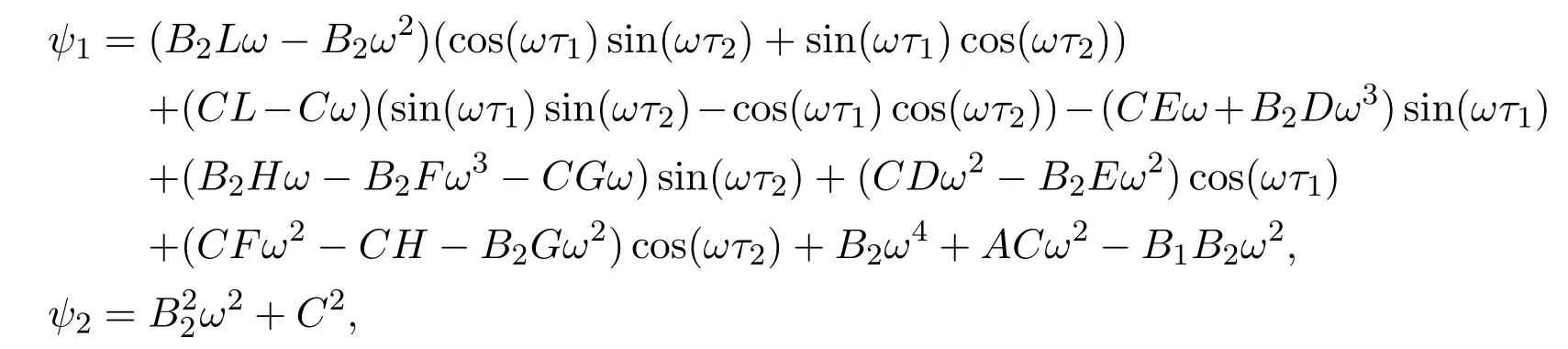
then±iωiare a pair of purely imaginary roots of equation(3.1)when1,2,··· ,k,j=0,1,···}. Let

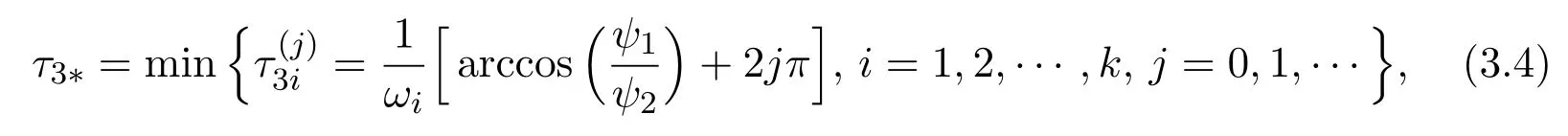
then equation (2.2) has a pair of purely imaginary root±iω3∗whenτ3=τ3∗. We differentiate both sides of equation (2.2) with respect toτ3and derive

where

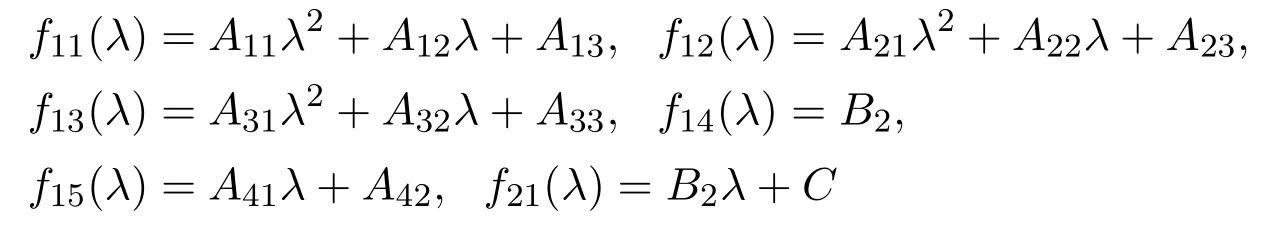
with

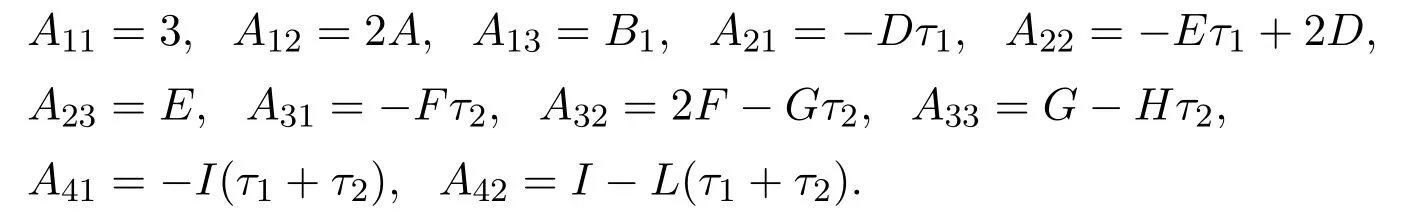
We have

where

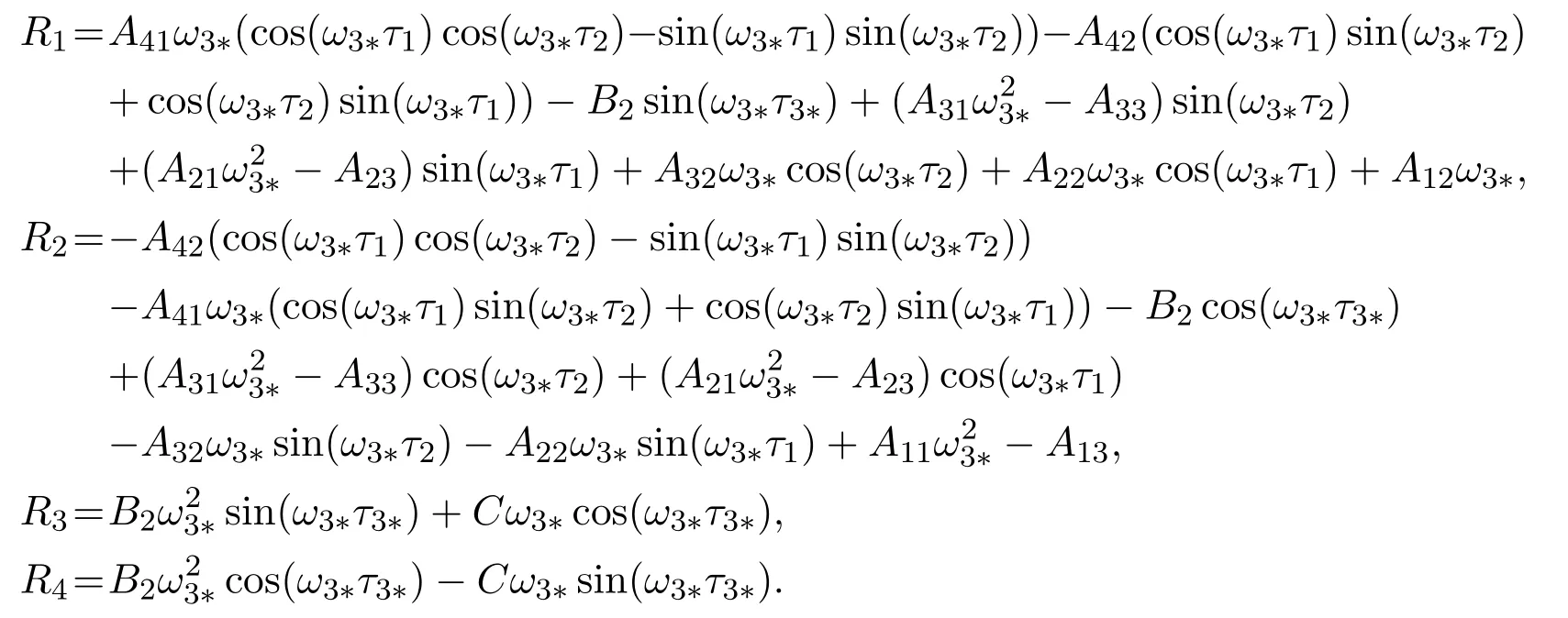
Suppose

We have the following results:

Theorem 3.1For system(1.1), we assume that(H1),(H2)hold, and suppose condition(i),(ii)in Lemma2.2,(H4),(H5)in[2],(H6),(H7)are satisfied, and τ1∈(0,τ10),τ2∈(0,τ2∗),then there exists a δ>0such that the following conclusions hold:

(i)The positive equilibriumof system(1.1)is asymptotically stablewhen τ3∈(0,τ3∗)and unstable when τ3∈[τ3∗,τ3+δ).

(ii)System(1.1)can undergo Hopf bifurcation atwhen τ3=τ3∗.

4 Direction and Stability of Hopf Bifurcation

Now we should study the property of Hopf by center manifold theorem and normal form [18]. We assumeτ2< τ1< τ3∗, whereτ2∈(0,τ2∗), τ1∈(0,τ10), then system (1.1) undergoes Hopf bifurcation atE∗whenτ3=τ3∗.

Letτ3=τ3∗+µ, t=sτ3,ui(sτ3) =For convenience, denotingasui(t), system (2.1) could be written inC([−1,0],R3),

Lµ:C →R3,f:R×C →R3are given respectively

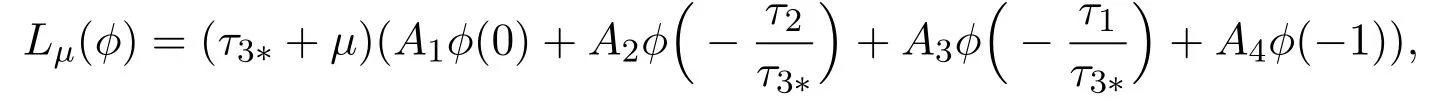
where

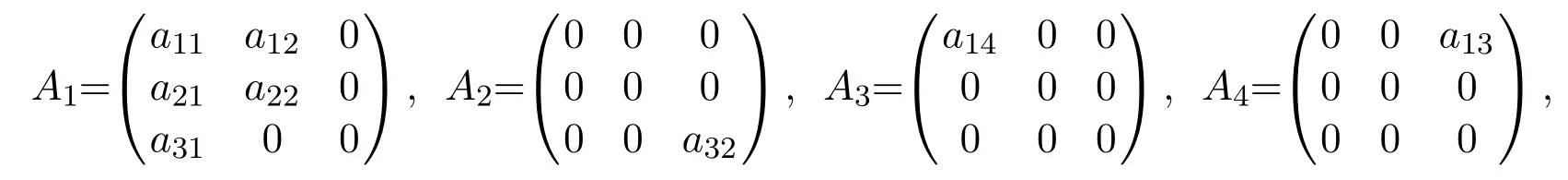
and

where

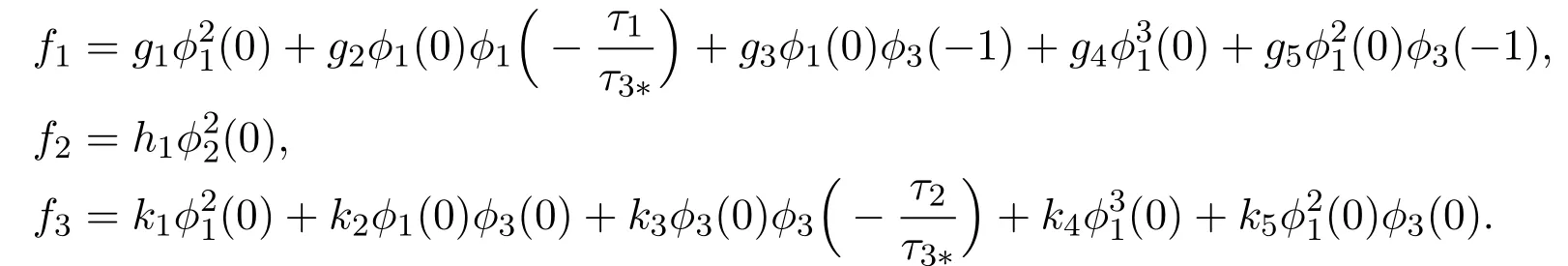
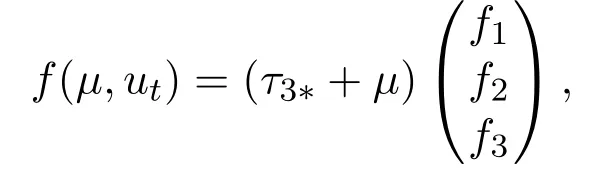
By Riesz representation theorem, there exists aη(θ,µ) of bounded variation forθ ∈[−1,0] such that

forϕ ∈C([−1,0],R3). In fact, we choose

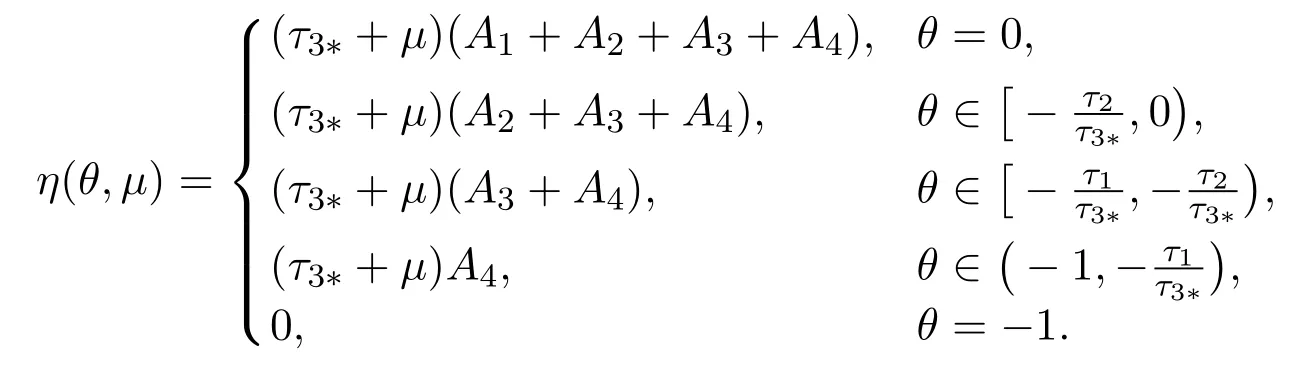
Forϕ ∈C1([−1,0],R3), define

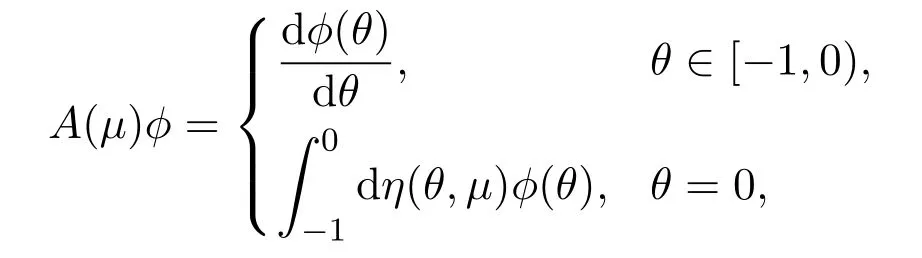
and

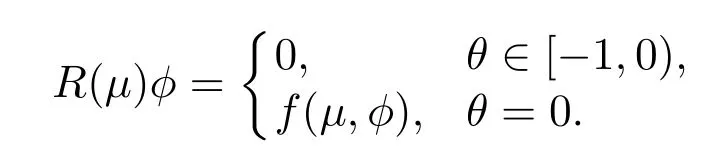
Then system (4.1) can be written as

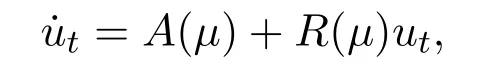
Forψ ∈C1([0,1],(R3)∗), define

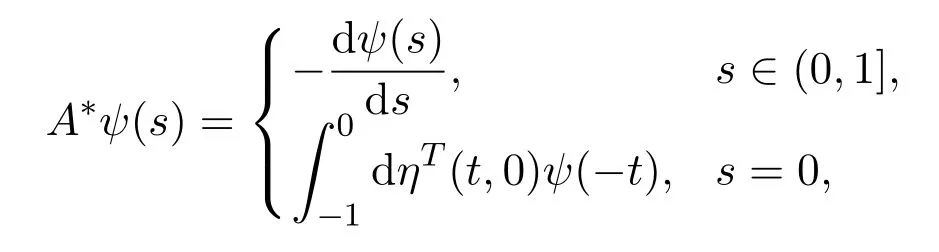
and a bilinear inner product

whenη(θ) =η(θ,0), thenA(0),A∗(0) are adjoint operators, From Section 3, we know±iω3∗τ3∗are eigenvalues ofA(0), thus they are also eigenvalues ofA∗(0). We compute the eigenvector ofA(0) andA∗(0) corresponding toiω3∗τ3∗and−iω3∗τ3∗.

Suppose thatq(θ) = (1,q2,q3)eiω3∗τ3∗θis the eigenvector ofA(0) corresponding toiω3∗τ3∗, by computing we obtain

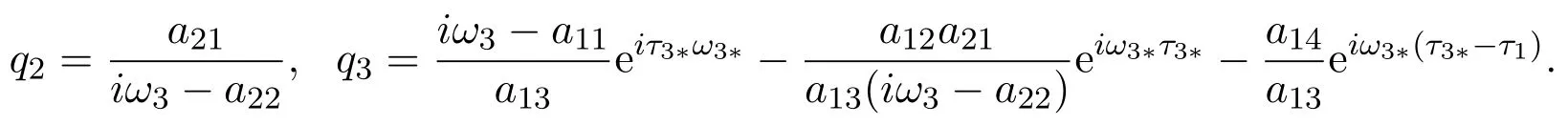
On the other hand, supposingwe obtain

Fromwe compute the value

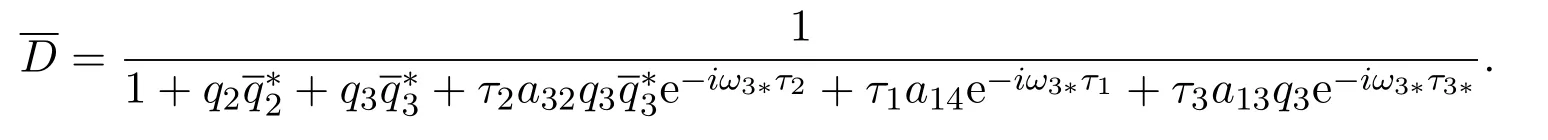
We compute center manifoldC0atµ=0, letutbe a solution of equation (4.1), and define

on the center manifoldC0, then we have

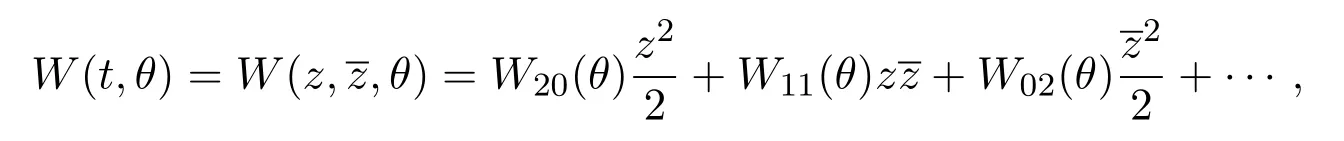
whereare the local coordinates for center manifoldC0in the direction ofq∗andWe noteW(t,θ) is real ifutis real. We consider only real solution, for the solutionut ∈C0of equation (4.1), sinceµ=0

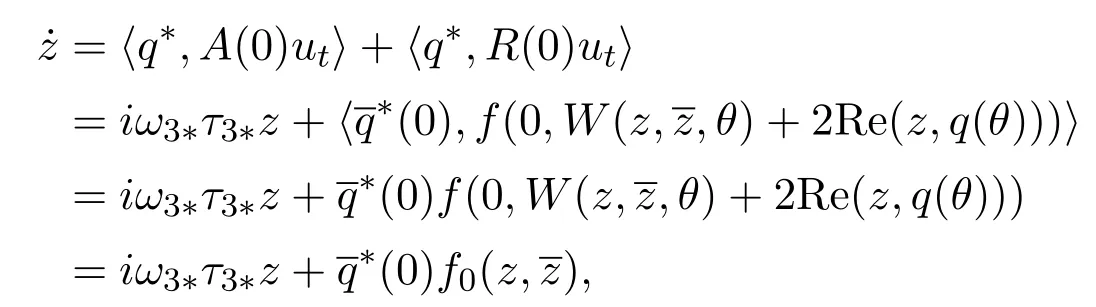
we write equation

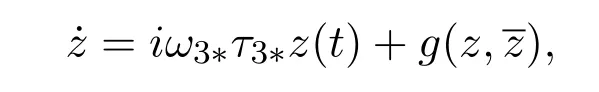
where

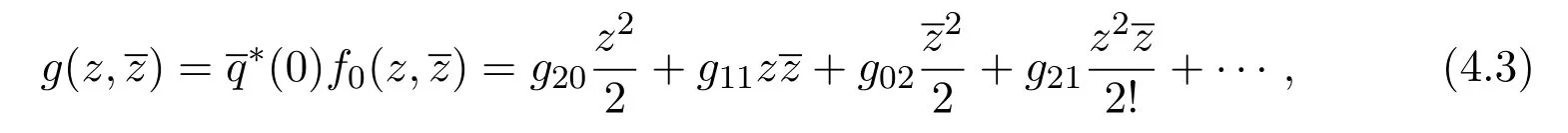
then

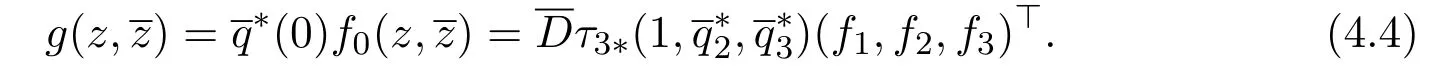
Fromut(θ)=(u1t(θ),u2t(θ),u3t(θ))=W(t,θ)+zq(θ)+we have

From (4.3),(4.4) we have

where

Comparing the above coefficients with (4.3), we obtain

with

whereE1,E2could be determined by

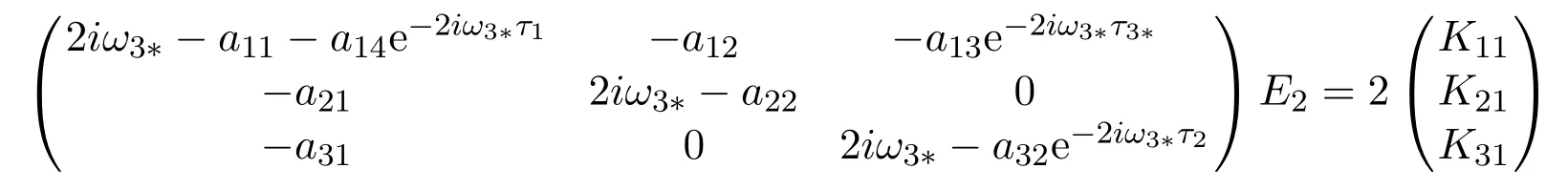
and

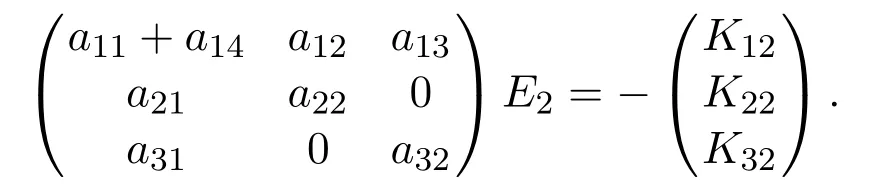
Then we can calculate the following value according to the above analysis:

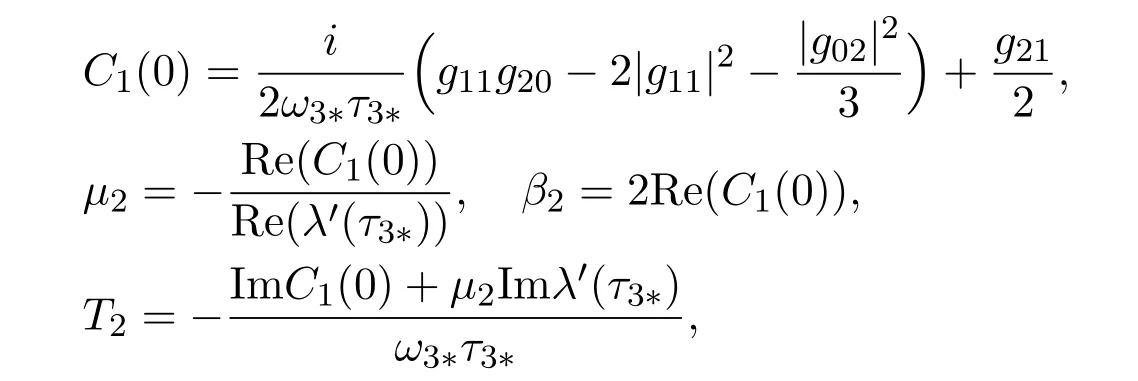
so we have the following result [18]:

Theorem 4.1(i)The sign of µ2determines the direction of Hopf bifurcation,when µ2>0(<0), the bifurcation is supercritical(subcritical).

(ii)The sign of β2determines the stability of bifurcating periodic solution, when β2>0(<0), the bifurcating periodic solutions are unstable(unstable).

(iii)The sign of T2determines the period of bifurcating periodic solution, when T2>0(<0), the period of bifurcating periodic solutions increases(decreases).

5 Numerical Simulation

Now we give simulation of system(1.1),all the parameters are same to[2],system(1.1) becomes:

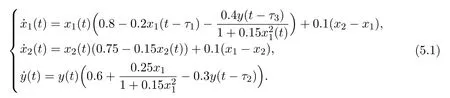
By computation,system(5.1)has two positive equilibriumsandIn [2], the author gave simulation aroundunder four cases: (1)τ1>0, τ2= 0, (2)τ1= 0, τ2>0, (3)τ1=τ2=τ >0, (4)τ1∈(0,τ10), τ2>0.

Now we give simulation aroundunder three cases: (1)τ1>0,τ2=0, τ3=0, (2)τ1∈(0,τ10), τ2>0, τ3=0, (3)τ1∈(0,τ10), τ2∈(0,τ2∗), τ3>0.

In case (1), we getτ10=1.970 98. Whenτ1=1.9<1.970 98,is locally asymptotically stable, whenτ1= 2.0>1.970 98, Hopf bifurcation occurs and periodic orbits bifurcate fromwhich are illustrated by Figures 1 and 2.

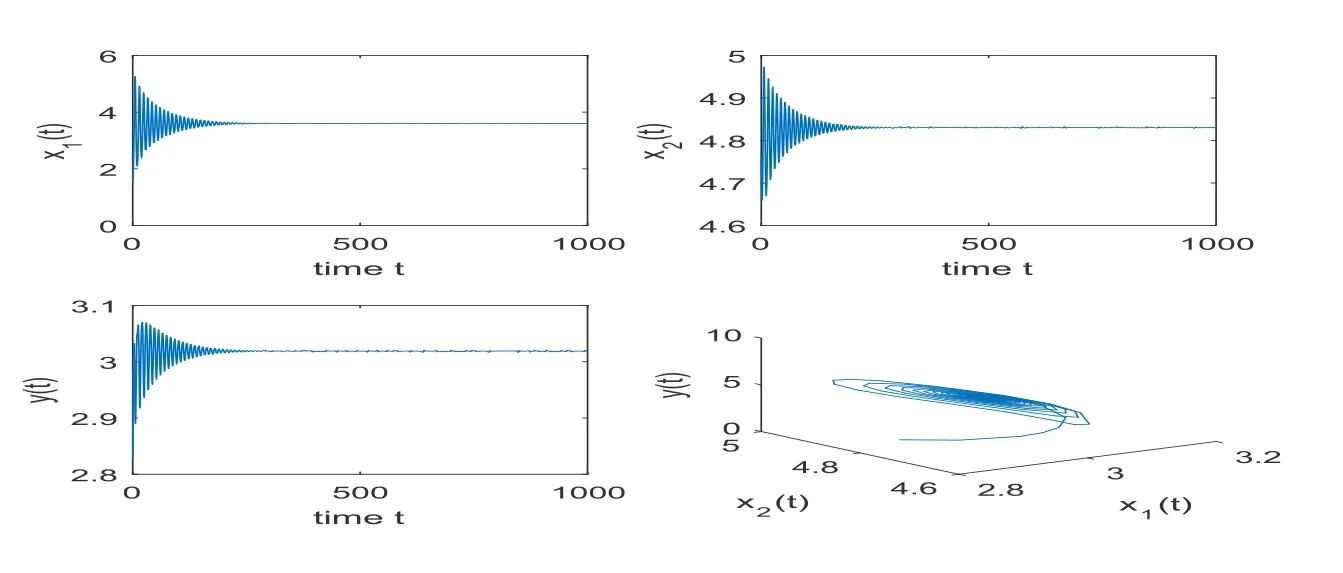
Figure 1: When τ1=1.9<τ10 =1.97098,τ2=0,τ3 =0, is locally asymptotically stable.

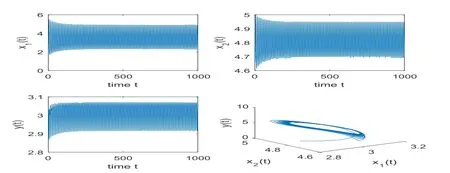
Figure 2: When τ1 =2.0>τ10 =1.970 98,τ2 =0,τ3 =0,the periodic solutions bifurcates from .

In case (2), fixingτ1= 1.93∈(0,τ10), we getτ2∗= 1.365 92. Whenτ2= 0.6<τ2∗,is locally asymptotically stable;whenτ2=1.5>τ2∗,Hopf bifurcation occurs and periodic orbits bifurcate from, which are illustrated by Figures 3 and 4.

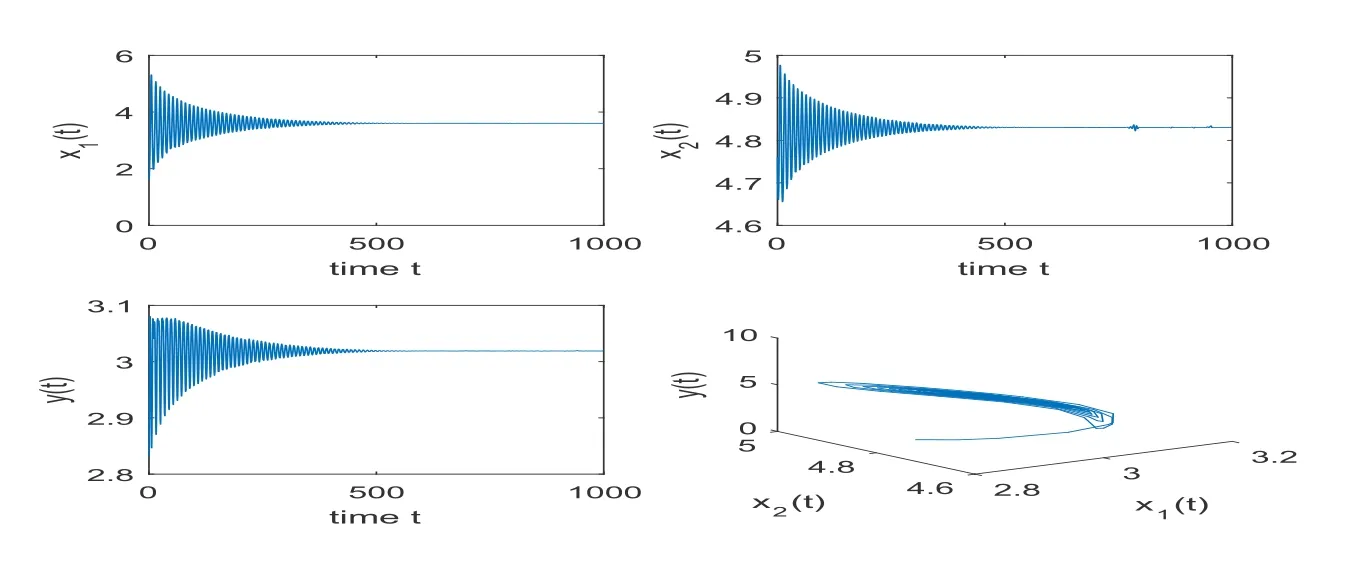
Figure 3: When τ1 =1.93∈(0,τ10),τ2 =0.6<τ2∗=1.365 92,τ3 =0,is locally asymptotically stable.

Figure 4: When τ1 =1.93 ∈(0,τ10),τ2 =1.5>τ2∗=1.365 92,τ3 =0,the periodic solutions bifurcates from .

In case (3), fixingτ1= 1.94∈(0,τ10), τ2= 1∈(0,τ2∗), we getτ3∗= 5.599 73.

Whenτ3= 5.0< τ3∗,is asymptotically asymptotically stable; whenτ3= 8.0>τ3∗, Hopf bifurcation occurs and periodic orbits bifurcate from, which are illustrated by Figures 5 and 6. In addition we getµ2=−4.442 68∗103.β2=3.001 2∗103,T2= 5.031 68∗102. From Theorem 4.1, the Hopf bifurcation is subcritical, the bifurcating periodic solutions are unstable, and the period of the bifurcating periodic solutions increases.

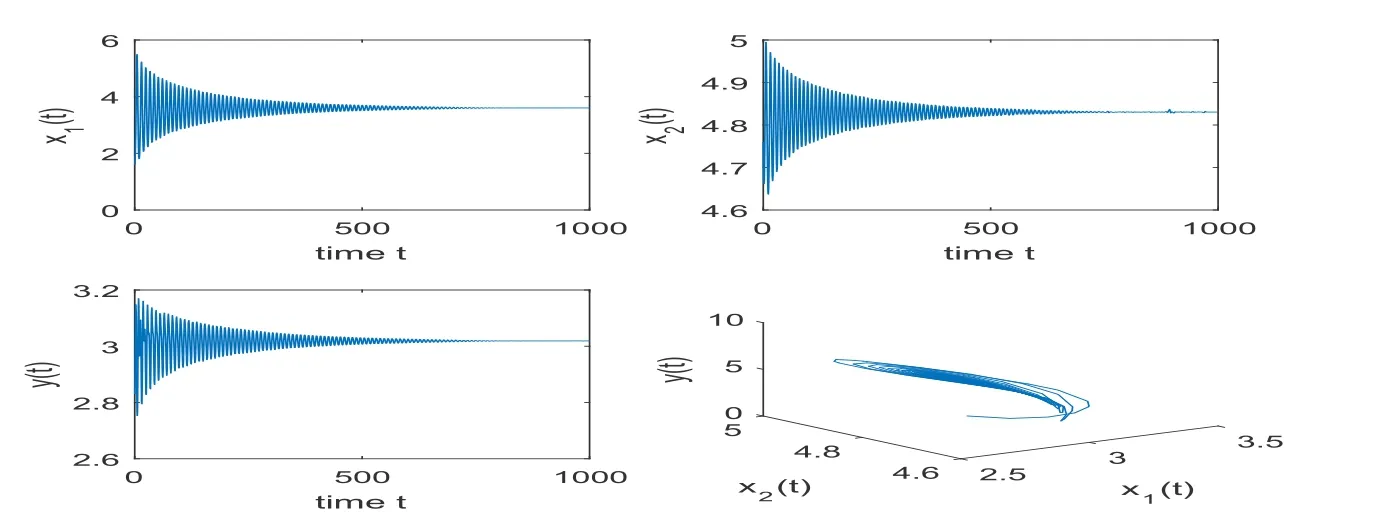
Figure 5: Whe nτ1 =1.94 ∈(0,τ10),τ2 =1.0∈(0,τ2∗),τ3 =5.0<τ3∗, is locally asymptotically stable.

Figure 6: When τ1 =1.94 ∈(0,τ10),τ2 =1.0 ∈(0,τ2∗),τ3 =8.0>(0,τ3∗),the periodic solutions bifurcates from .

6 Conclusion

In this paper, we analyse Hopf bifurcation in a Monold-Haldane predator-prey model with three delays and diffusion. First we give the description of this system and then based on the work[2]we give the dynamics of this system with three delays under two cases: (1)τ >0, τ2=0, τ3=0, (2)τ1∈(0,τ10), τ2>0, τ3=0. Because whenτ3=0, the dynamics of system (1.1) were studied in [2], dynamics of case (1)and case (2) are similar to those of case (II) and case (IV) respectively. Then we discuss Hopf bifurcation of system(1.1)when three delays coexists and give the direction and stability of Hopf bifurcation by center manifold theorem and normal form.At last, we conclude that there exist two positive equilibria(1.026,4.24,2.28),(3.6,4.83,3.01) and give the simulation around(3.6,4.83,3.01) under three cases: (1)τ1>0, τ2=0, τ3=0, (2)τ1∈(0,τ10), τ2>0, τ3=0, (3)τ1∈(0,τ10),τ2∈(0,τ2∗), τ3= 0 to support our results. We know that the work about Hopf bifurcation with two delays are interesting. But the work about three delays should be more interesting and real contrary to [2].

Recently there exist many works about dynamics of predator-prey system. As we know, time delay always exists, so the dynamics of predator-prey system with delay should be more real. Besides diffusion exist under case that more than one kind of preys in different patches and the predator only prey on one prey, so we use system (1.1) to describe predator-prey system with diffusion. During these delays,one is the feedback of prey, the other one denote the feedback of predator and the last one denote the hunting delay for predator. Our result suggest that every delay could lead instability for system, and delay has great influence on the dynamics of predator-prey system. So how to control delays should be important for the stability of predator-prey system. When the delays are sufficiently small,equilibrium point is stable,but once one delay cross corresponding critical value,Hopf bifurcation occurs for system.