WEAK AND SMOOTH GLOBAL SOLUTION FOR LANDAU-LIFSHITZ-BLOCH-MAXWELL EQUATION∗†
2020-03-14BolingGuoYongqianHanDaiwenHuang
Boling Guo, Yongqian Han, Daiwen Huang
(Institute of Applied Physics and Computational Math., P.O. Box 8009,Beijing 100088, PR China)
Fangfang Li‡
(Institute of Applied Math., Academy of Math. and Systems Science,China Academy of Sciences, Beijing, 100190, PR China)
Abstract This paper is devoted to investigate the existence and uniqueness of the solution of Landau-Lifshitz-Bloch-Maxwell equation. The Landau-Lifshitz-Bloch-Maxwell equation, which fits well for a wide range of temperature, is used to study the dynamics of magnetization vector in a ferromagnetic body.If the initial data is in (H1,L2,L2), the existence of the global weak solution is established. If the initial data is in(Hm+1,Hm,Hm)(m ≥1), the existence and uniqueness of the global smooth solution are established.
Keywords Landau-Lifshitz-Bloch-Maxwell equation;global solution;paramagnetic-ferromagnetic transition; temperature-dependent magnetic theory;Landau-Lifshitz theory
1 Introduction
In this paper, we consider the periodic initial value problem of the following equations
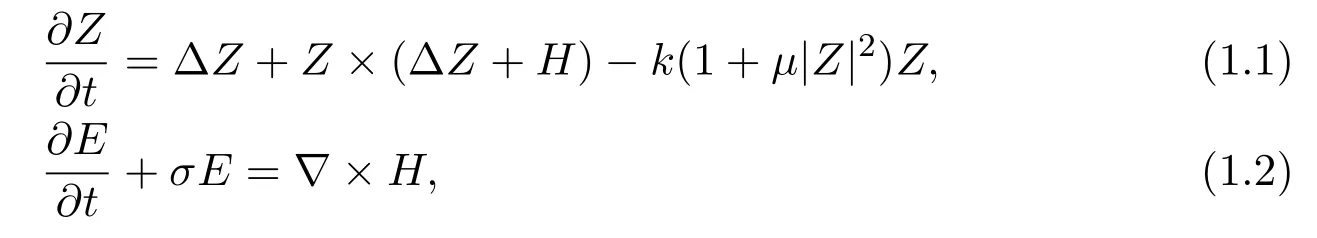
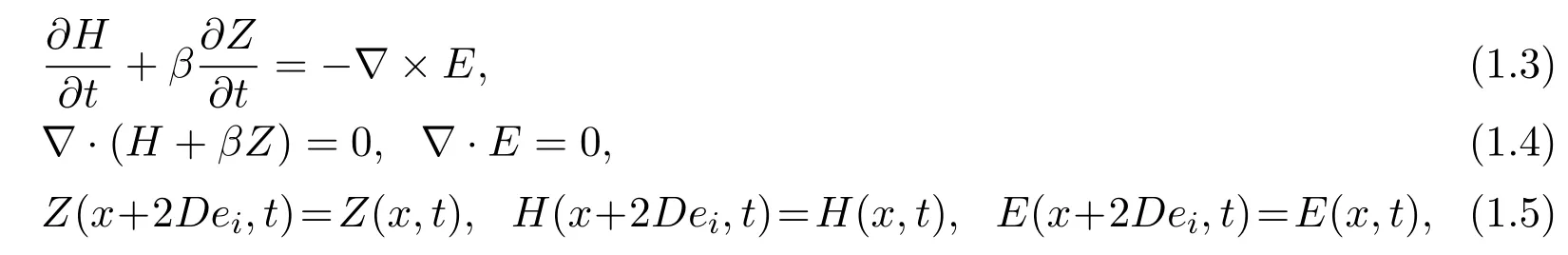
with the initial conditions

whereσ,k,µ,βare positive constants,Z ∈R3is the spin polarization,H(x,t) =(H1,H2,H3) is the magnetic field,E(x,t)=(E1(x,t),E2(x,t),E3(x,t)) is the electric field andHe= ∆Z+His the effective magnetic field.x ∈Ω⊂Rd,d= 2,3,
Here the operator∇is defined as follows:
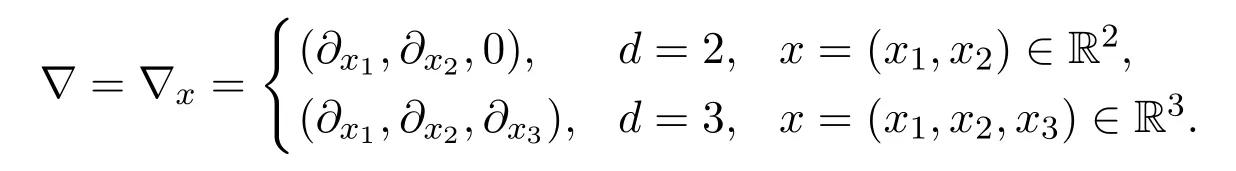
System (1.1)-(1.4) was studied in [4] under the additional assumption that temperature is equal to constant. In [3,4], Berti et. al. proposed a model for the study of the dynamics of magnetization vector in a ferromagnetic body. This model fits well for a wide range of temperature, and then can be used to establish a link between micromagnetics and the phase transition occurring from paramagnetic to ferromagnetic regimes.
System (1.1)-(1.4) generalizes some classical models for magnetically saturated bodies such as the well known Landau-Lifshitz equation. Landau-Lifshitz equation well describes the magnetization dynamics of ferromagnet at low temperature [22].The Landau- Lifshitz-Gilbert equation is described as follows

whereM(x,t) = (M1(x,t),M2(x,t),M3(x,t)) is a magnetization vector,λ >0 is a Gilbert constant, “×” denotes the vector outer product. Equation (1.7) has been investigated widely. Many important results have been obtained, see [6,17,20,21]and therein references.
Equation (1.7) withλ= 0 is so-called Schr¨odinger map [5]. This Schr¨odinger map has been widely studied in [1,2,5,7,8,19,21,24–26] and therein references.
The model of [4] is very close to the Landau-Lifshitz-Bloch (LLB) equation. In order to describe the dynamics of magnetization vectorZin a ferromagnetic body for a wide range of temperature,Garanin et. al.[10–12]derived the Landau-Lifshitz-Bloch(LLB)equation from statistical mechanics with the mean field approximation.At high temperature (θ ≥θc,θc-Curie value), the LLB model is commonly used to describe the dynamics of magnetic fields with non-constant modulus.
The LLB equation is given as follows
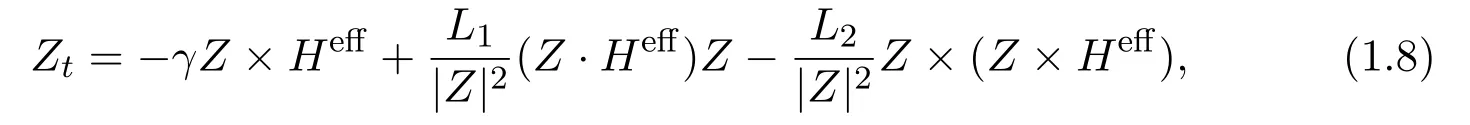
whereγ, L1, L2are constants,γis the gyromagnetic ratio,Heffis the effective field.By introducing the dimensionless fieldz, (1.8) can be rewritten as follows
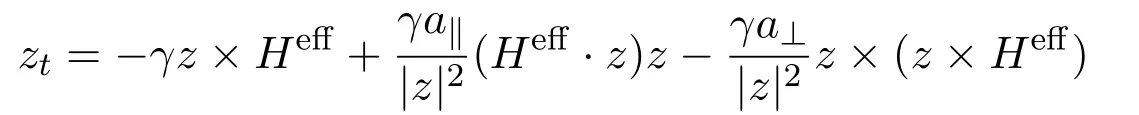
withγa∥=L1,γa⊥=L2. Herea∥anda⊥are dimensionless damping parameters that depend on the temperature, and are defined as follows [3]
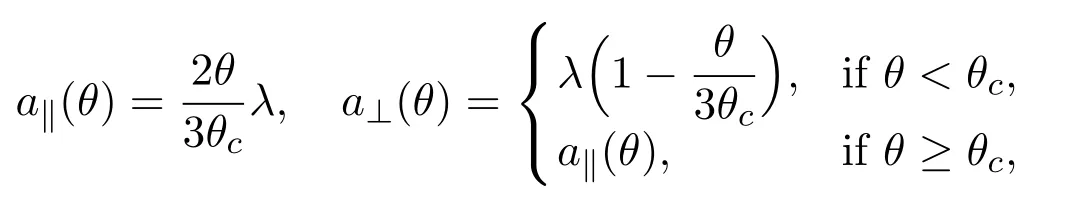
whereλ>0 is a constant. In [23], the author pointed that ifL1=L2, (1.8) can be reduced as follows
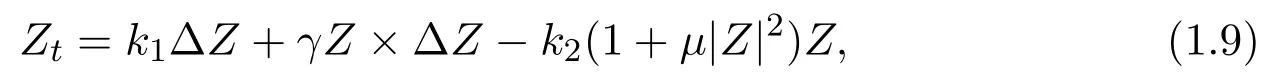
wherek1>0, k2>0, γ >0, µ >0. The existence of weak solution for equation(1.9) has been obtained in [23]. Equation (1.9) withk= 0 is used to discuss the hydrodynamics of Heisenberg paramagnet, see [9] and therein references. The existence and uniqueness of global smooth solution of equation (1.9) withk= 0 were established in [18].
Inspired by the ideas in[13–17],we will consider the existence of the global weak solution and the global smooth solution of Landau-Lifshitz-Bloch-Maxwell equation(1.1)-(1.6).
Note that system (1.1)-(1.4) is over-determined. Therefore we have to assume that the initial functionsZ0,H0andE0satisfy the following equations
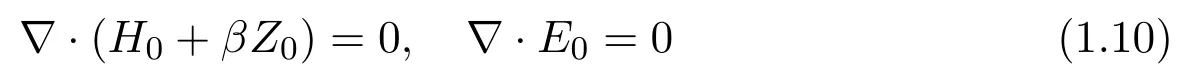
in distribution.
Let (Z0,H0,E0)∈(Hm+1,Hm,Hm). Form= 0, the existence of global solutions of problem (1.1)-(1.6) is proved.
Theorem 1.1Assume that, and(1.10)is satisfied. The constants k,σ,µ,β are positive. Then theperiodic initial value problem(1.1)-(1.6)has at least one global generalized solution(Z(x,t),H(x,t),E(x,t))such that

Theorem 1.2Assume that Z0(x)∈H1(Rd), H0(x)∈L2(Rd), E0(x)∈L2(Rd),and(1.10)is satisfied. The constants k,σ,µ,β are positive. Then there exists a global generalized solution(Z(x,t),H(x,t),E(x,t))of the initial value problem(1.1)-(1.4)(1.6)such that
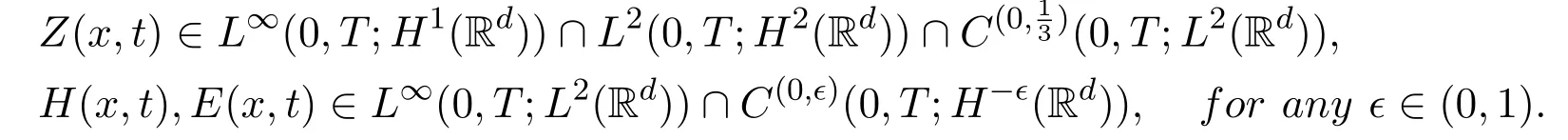
For more regular initial data, that ism ≥1, not only the existence but also the uniqueness of global solution of problem (1.1)-(1.6) are proved.
Theorem 1.3Assume that d=2,Ω⊂R2, k,µ,σ,β>0,(Z0(x),H0(x),E0(x))∈m ≥1, and(Z0,H0,E0)satisfies(1.10). Then thereexists a unique global solution(Z,H,E)of the periodic initial value problem(1.1)-(1.6). Moreover, we have
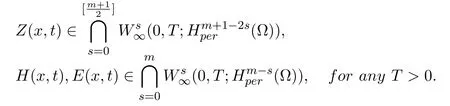
Theorem 1.4Assume that d= 2, k,µ,σ,β >0,(Z0(x),H0(x),E0(x))∈
(Hm+1(R2), Hm(R2), Hm(R2)), m ≥1, and(Z0,H0,E0)satisfies(1.10). Then there exists a unique global solution(Z,H,E)of the initial value problem(1.1)-(1.4)(1.6). Moreover, we have
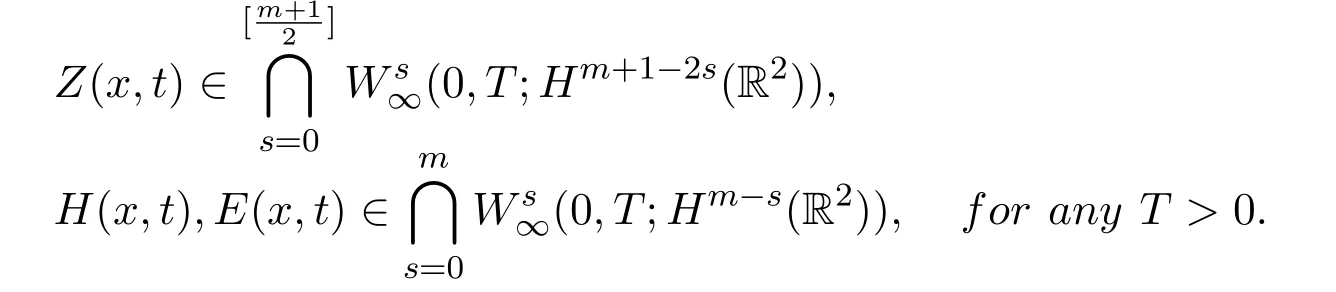
Theorem 1.5Assume that d=3,Ω⊂R3,k,µ,σ,β>0,(Z0(x),H0(x),E0(x))∈m ≥1,(Z0,H0,E0)satisfies(1.10), and there existsa positive constant δ0≪1such thatThen there exists a uniqueglobal solution(Z,H,E)of the periodic initial value problem(1.1)-(1.6). Moreover,we have
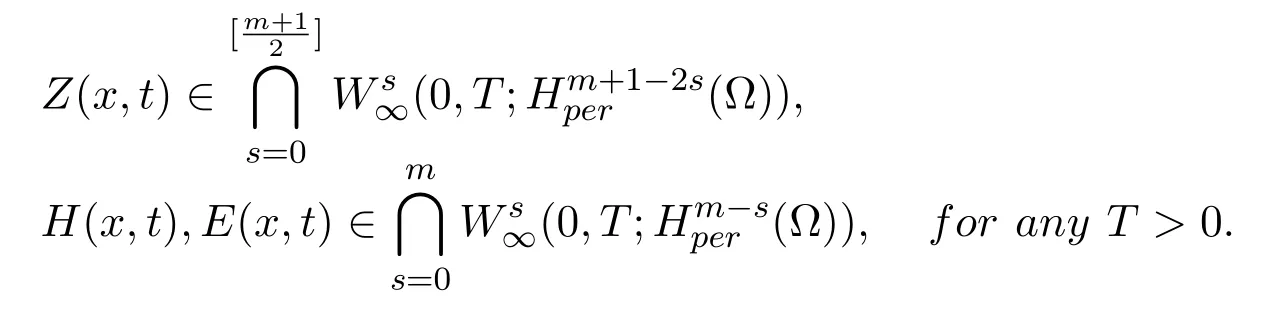
Theorem 1.6Assume that d= 3, k,µ,σ,β >0,(Z0(x),H0(x),E0(x))∈
(Hm+1(R3), Hm(R3), Hm(R3)), m ≥1,(Z0,H0,E0)satisfies(1.10), and there ex-ists a positive constant δ0≪1such thatThen there exists a uniqueglobal solution(Z,H,E)of the initial value problem(1.1)-(1.4) (1.6). Moreover, we have
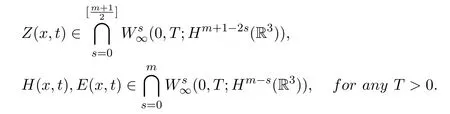
Remark 1.1In Theorems 1.5 and 1.6, we only assume thatis small enough, no matter the size of (H0,E0) and(m ≥0). Indeed,Z0can be highly oscillatory initial value. For example,
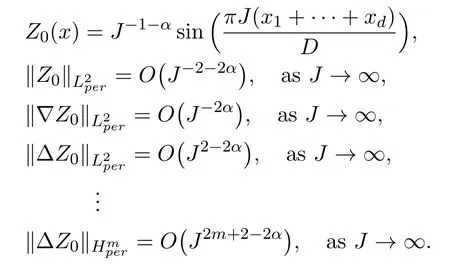
Ifα ∈(0,1/2), thenZ0satisfies the condition of Theorem 1.5 withJ ≫1, that isis large enough withJ ≫1.
In the proofs of Theorems 1.1-1.6, the main difficulties are that system (1.1)-(1.4) is over-determined and equation (1.1) is quasi-linear. The over-determination is overcame by using the conservation of Maxwell equation (1.2)-(1.4). Other main ingredients, which are applied to obtain a priori uniform estimates, consist of the symplectic structure of the termZ×∆Z,the dissipation of the term−k(1+µ|Z|2)Zand the regularity which is derived from the term ∆Zof equation (1.1).
In order to solve problem (1.1)-(1.6), let us introduce the following transformation

and rewrite equations (1.1)-(1.6) as follows
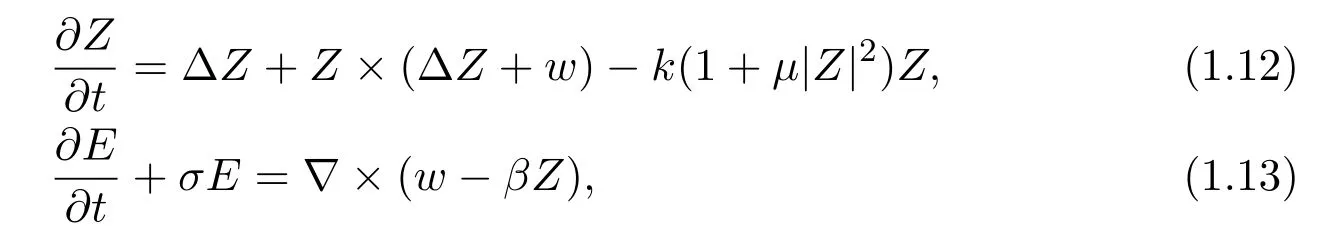
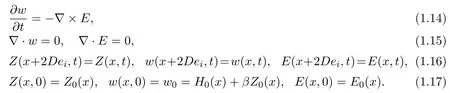
We first construct the solutions of equations (1.12)-(1.14) with (1.16) (1.17),and then prove that these solutions satisfy equation (1.15) under condition (1.10).Consequently, we get that there exist solutions of problem (1.12)-(1.17).
This paper is organized as follows. In Section 2, the Galerkin approximate solutions of problem (1.12)-(1.14) with (1.16) (1.17) are constructed, and a priori uniform estimate of these solutions in (H1,L2,L2) is established. In Section 3, the existence of the generalized solutions of problem (1.12)- (1.17) is proved. Consequently, Theorems 1.1 and 1.2 are proved. In Section 4, a priori uniform estimates of the Galerkin approximate solutions in (Hm+1,Hm,Hm) (m ≥1) are established,and the existence and uniqueness of the global solution of problem (1.12)-(1.17) are proved. Consequently, Theorems 1.3-1.6 are obtained.
2 Approximate Solutions and A Priori Estimates for the Periodic Initial Value Problem
We use Galerkin method to solve equations (1.12)-(1.14) with (1.16) (1.17). In this section, we first establish aprioriestimates for the approximate solutions of(1.12)-(1.14) with (1.16) (1.17).
Letωn(x)(n= 1,2,···) be the unit eigenfunctions satisfying the equation

with periodicityωn(x−Dei)=ωn(x+Dei)(i=1,2,··· ,d),andλn(n=1,2,···)be the corresponding eigenvalues which are different from each other.{ωn(x)}consists of the orthogonal normal ofm=0,1,···.
Therefore
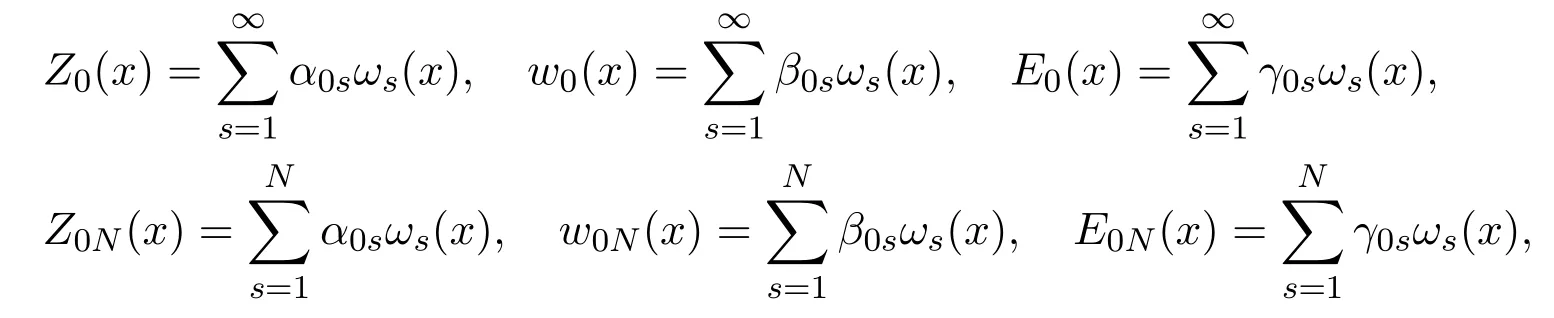
where

If (Z0,w0,E0)(m ≥0), then

Denote the approximate solution of problem (1.12)-(1.14) byZN(x,t),wN(x,t)andEN(x,t) defined in the following forms
HereαsN(t),βsN(t) andγsN(t) are three dimensional vector-valued functions,s=1,2,··· ,N, N=1,2,···, which satisfy the following system of ordinary differential equations of first order
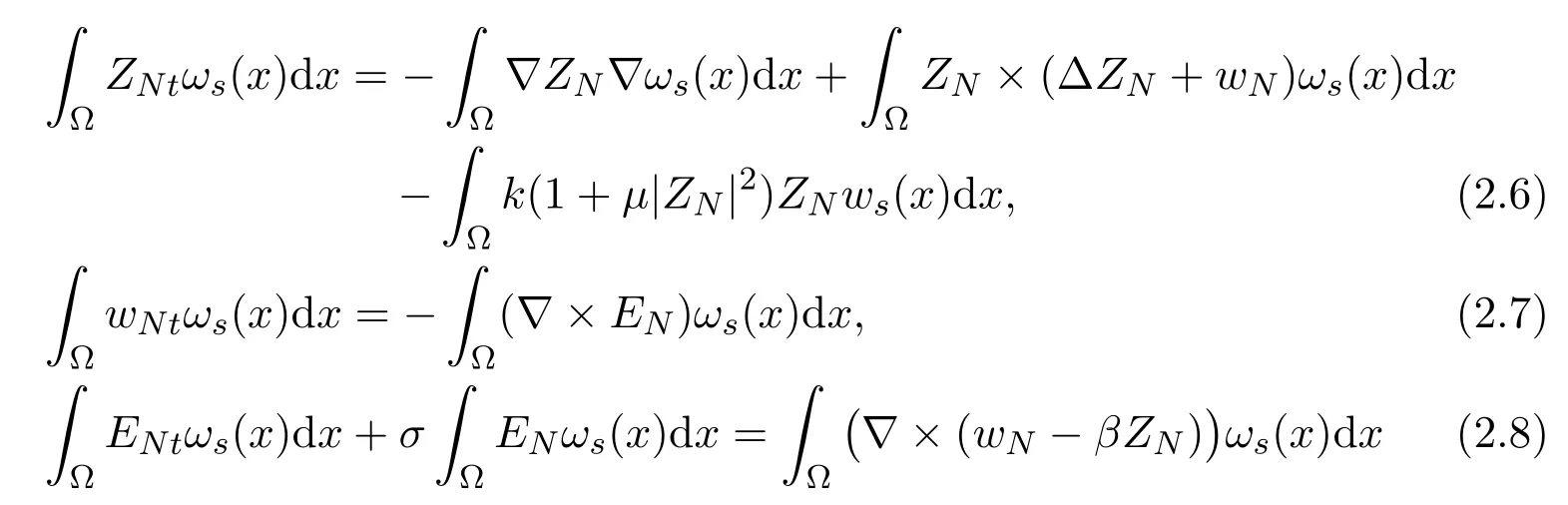
with the initial conditions
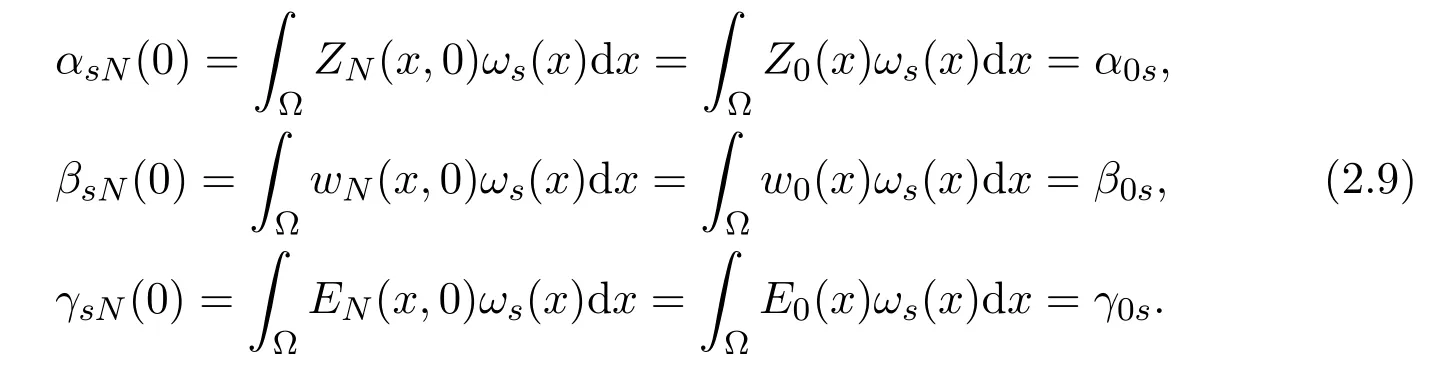
Obviously, we have
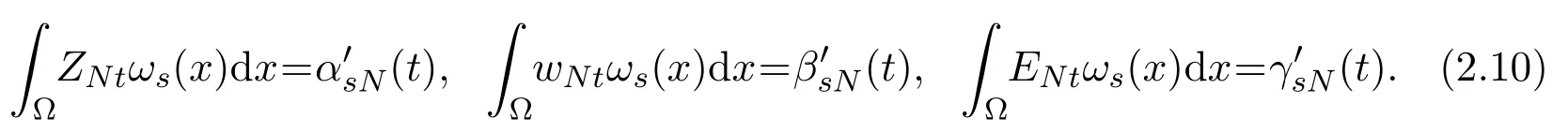
For simplicity, we introduce a notation as follows
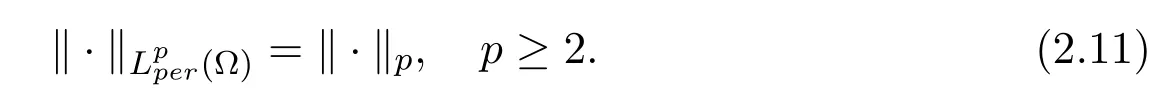
Lemma 2.1Assumethenfor the solutions of the initial value problem(2.6)-(2.9), we have the following estimate
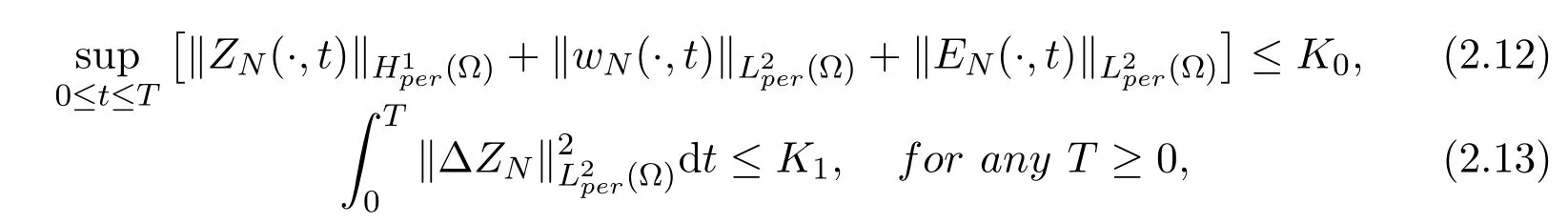
where K0and K1are constants which are independent of N and D.
ProofMultiplying (2.6) byαsN(t), and summing up the results with respect tos=1,2,··· ,N, we get
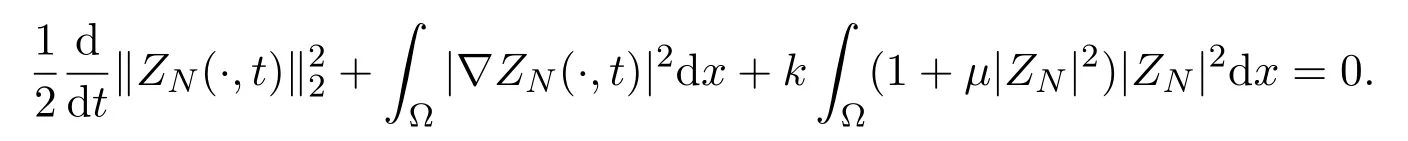
Sincek,µ>0, one has
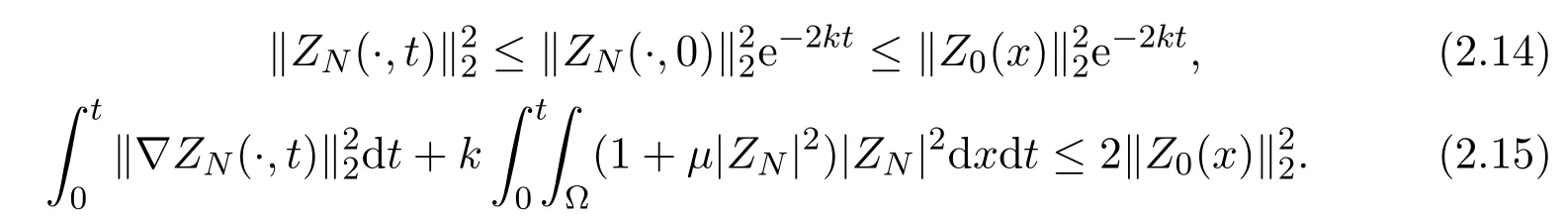
Making the scalar product ofβsN(t) with (2.7) and the scalar product ofγsN(t)with (2.8) respectively, adding the two obtained equalities, and then summing up the results with respect tos=1,2,··· ,N, we get
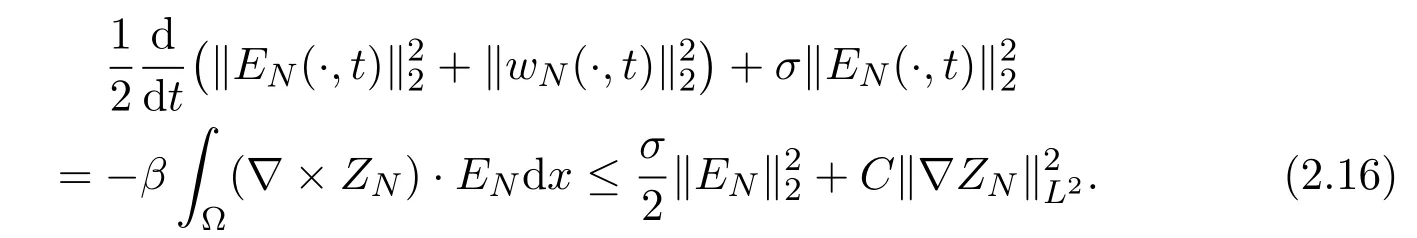
From (2.16) and (2.15), we have

Making the scalar product of−λsαsN(t)with(2.6),summing up the results with respect tos=1,2,···,N, and noticing that
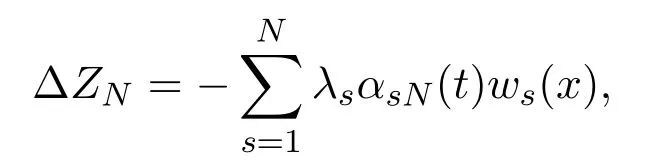
we have

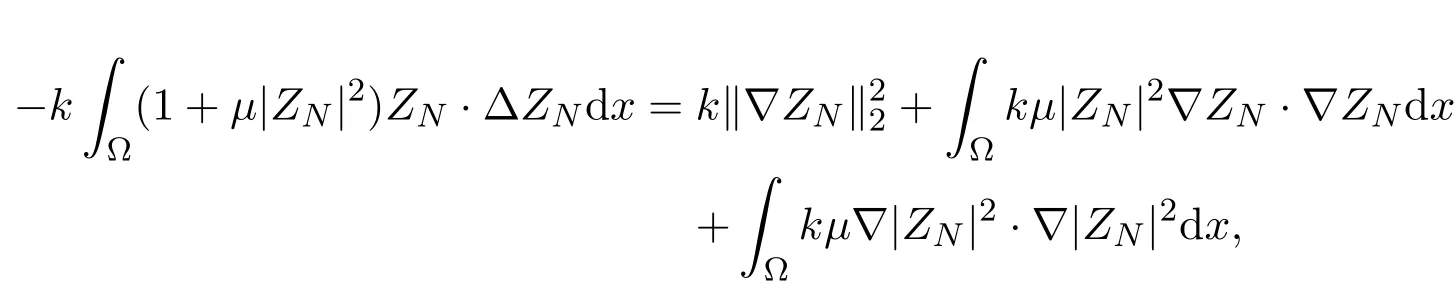
and then
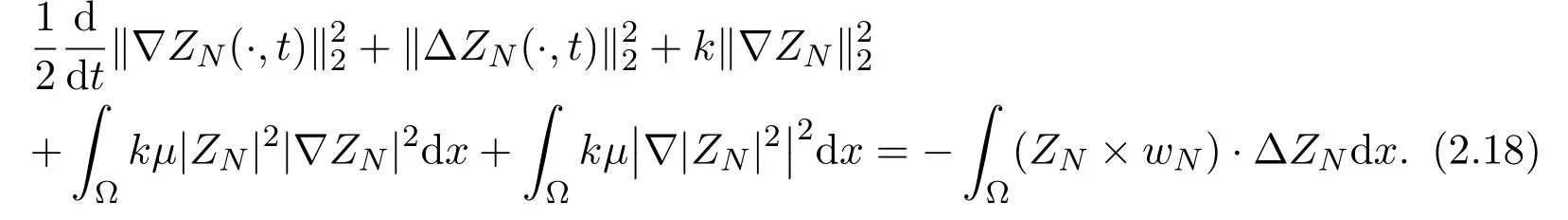
By Gagliardo-Nirenberg inequality and estimates (2.14) (2.17), we obtain

Applying (2.18) (2.19) and Gronwall inequality, we can prove estimates (2.12) and(2.13).
Lemma 2.2Assume that the conditions of Lemma2.1are satisfied. For the solution(ZN(x,t), wN(x,t),EN(x,t))of the initial value problem(2.6)-(2.9), there is the following estimate
ProofFor anyφ ∈φcan be represented as
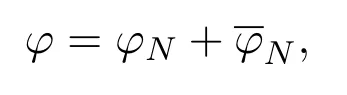
where
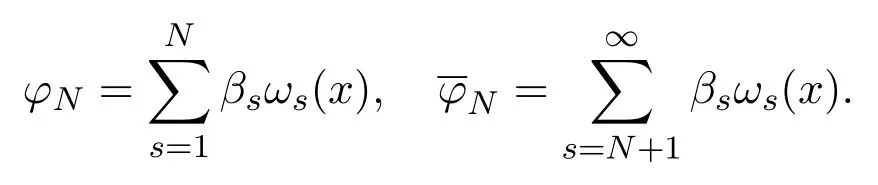
Fors ≥N+1, it yields that

Then by Lemma 2.1, there are the following estimates
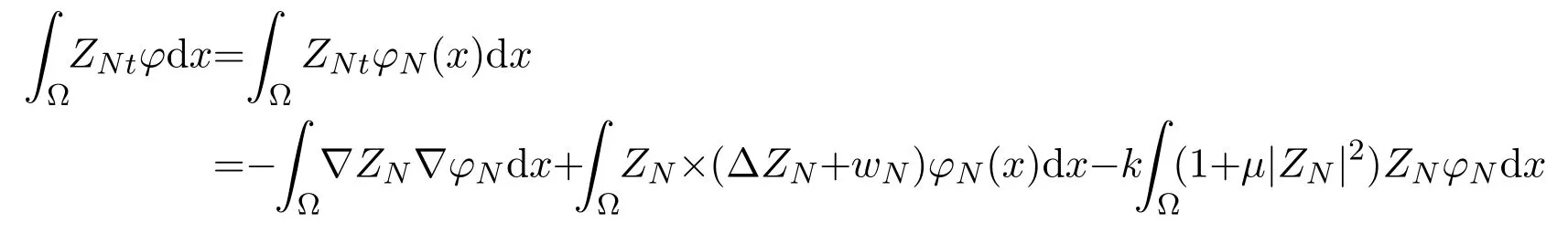
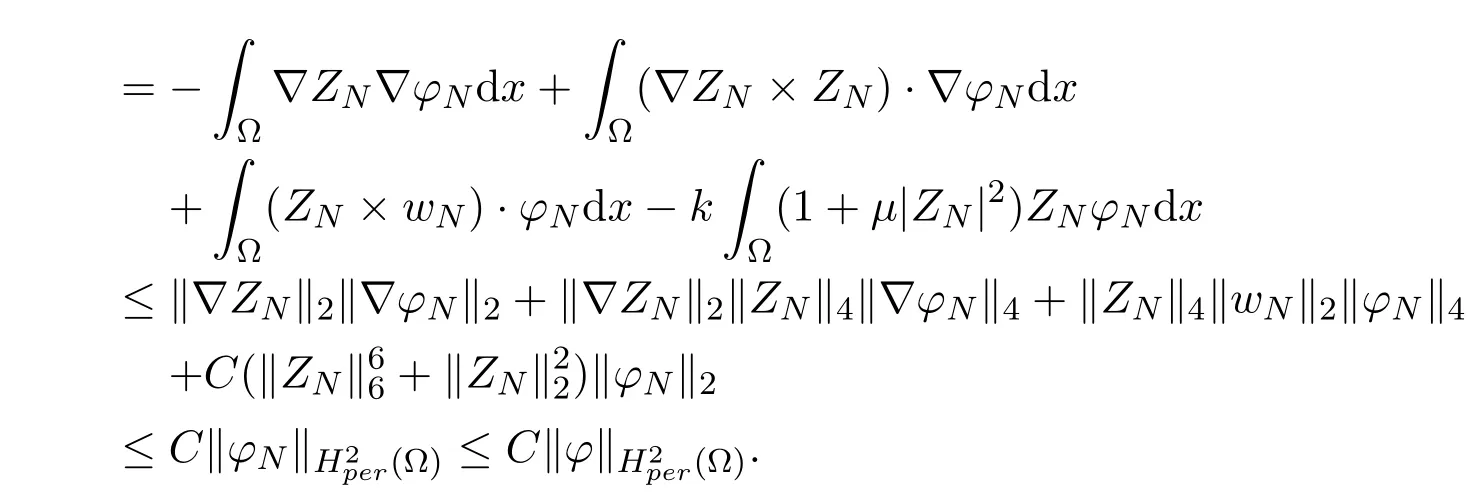
Similarly, fors ≥N+1, it yields that
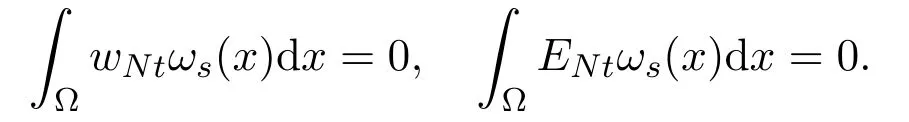
Then by Lemma 2.1, there are the following estimates

Thus the following estimate holds

This lemma is proved.
Lemma 2.3Assume that the conditions of Lemma2.1are satisfied. For the solution(ZN(x,t), wN(x,t),EN(x,t))of the initial value problem(2.6)-(2.9), there are the following estimates for any t1,t2≥0
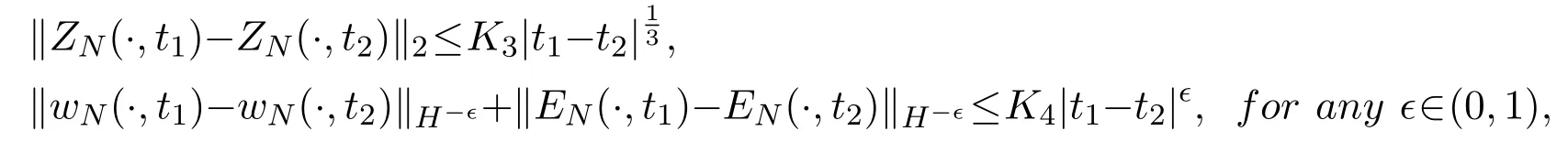
where the constants K3and K4are independent of N and D.
ProofBy the Sobolev interpolation inequality of negative order, it yields that
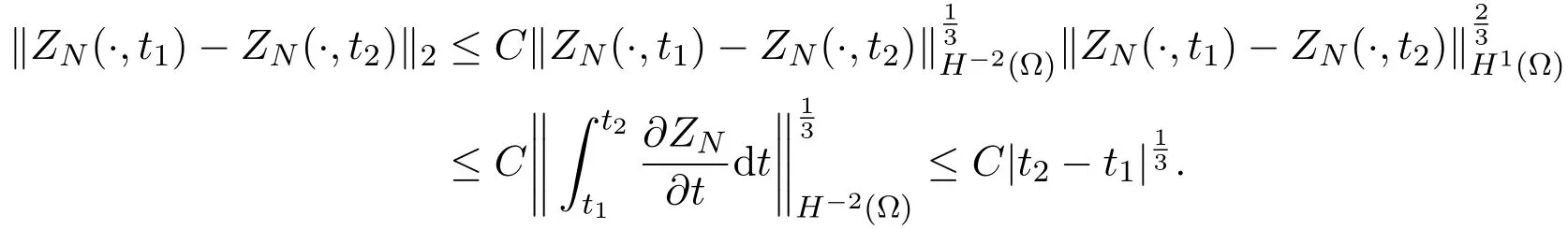
Similarly, for anyϵ ∈(0,1), we have
This lemma is proved.
By using the above estimates of the approximate solution, we have:
Lemma 2.4Under the conditions of Lemma2.1, there exists a unique global solution(αsN(t),βsN(t),γsN(t))(s=1,2,··· ,N, t ∈[0,T], for any T >0)of the initial value problem for the ordinary differential equations(2.6)-(2.9). Moreover this solution is continuously differentiable.
3 Existence of Generalized Solution
This section is devoted to prove the existence of the generalized solution for the periodic initial value problem (1.12)-(1.17). First we give the definition of the generalized solution.
Definition 3.1A triple of three-dimensional vector functions(Z(x,t),w(x,t),E(x,t)∈is called the generalized solution for the periodic initial value problem (1.12)-(1.17), if for any vector-valued test functionφ(x,t)and for any scalar test functionthe following equations hold
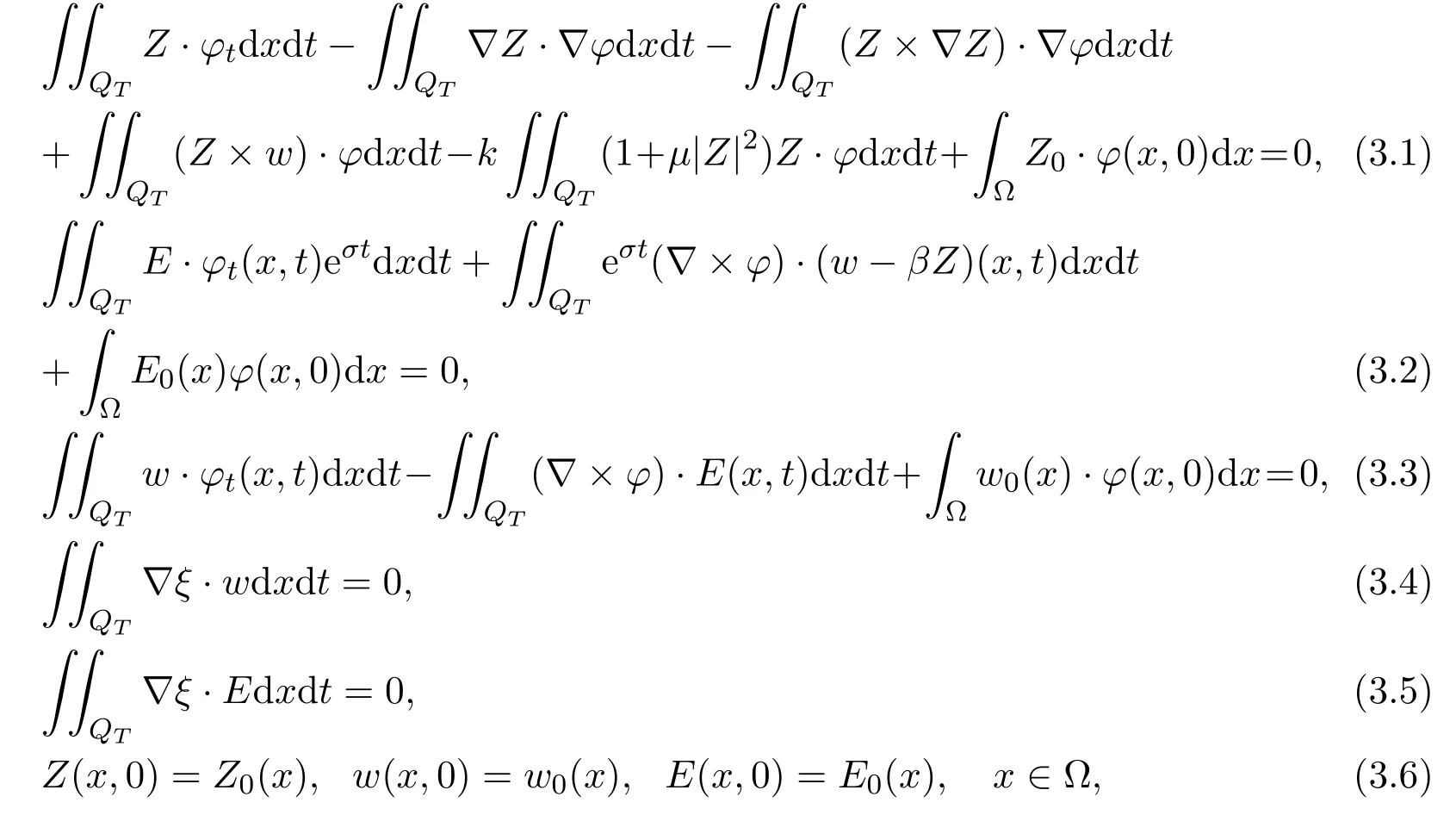
whereQT=Ω×[0,T].
Lemma 3.2Let the initial vector functions(Z0(x),H0(x),E0(x))satisfy the condition
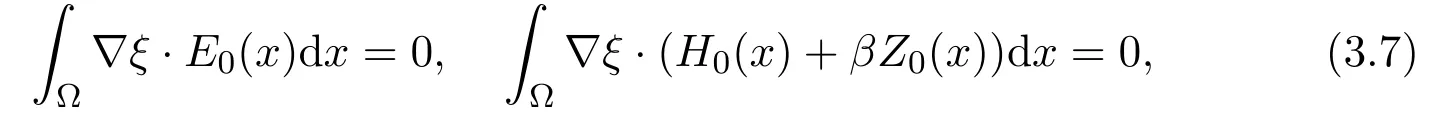
for all ξ(x)Then for anywith ξ(x,T)=0and ξ0=ξ(x,0), we have from(3.2)and(3.3)that
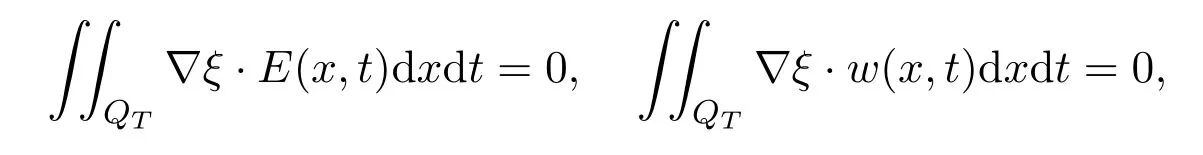
that is(3.4)and(3.5)hold.
ProofTake
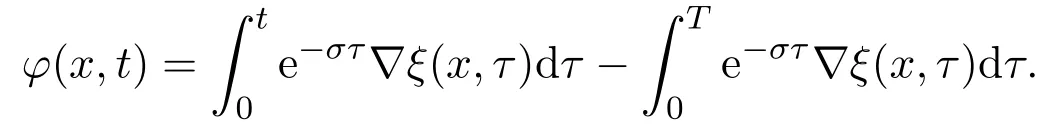
Noting thatby (3.2) we get
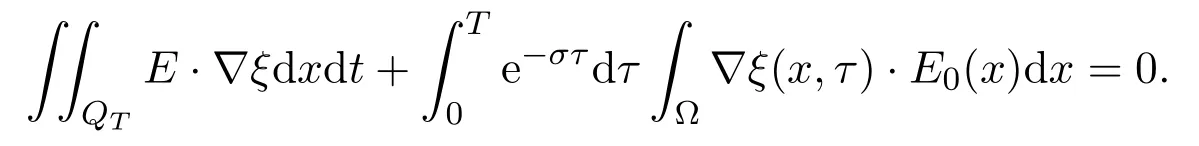
Since
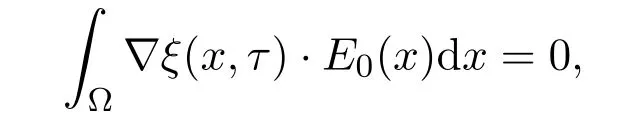
we obtain
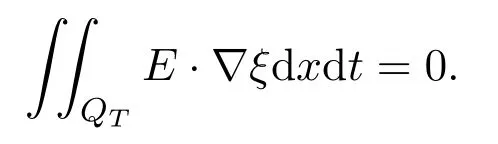
Letting
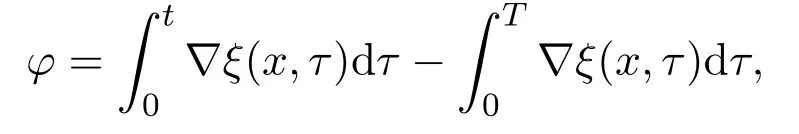
we have from (3.3)
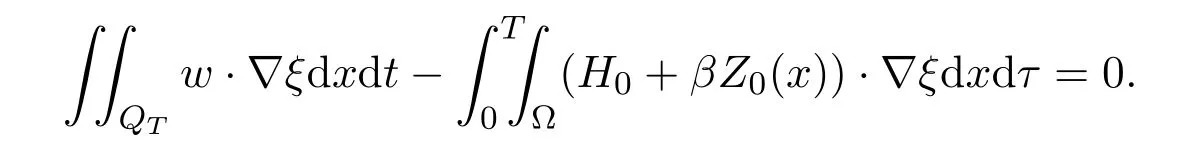
From
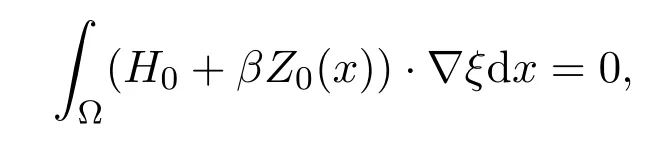
it follows that
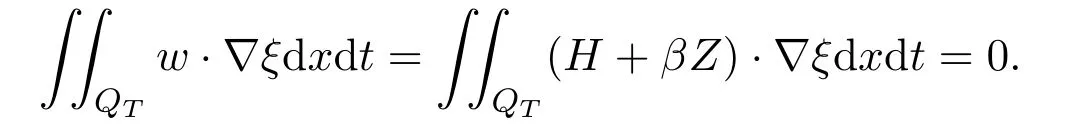
This lemma is proved.
Theorem 3.1Assume thatand(3.7)is satisfied. The constants k,σ,µ,β are positive. Then the pe-riodic initial value problem(1.12)-(1.17)has at least one global generalized solution(Z(x,t),w(x,t),E(x,t))such that
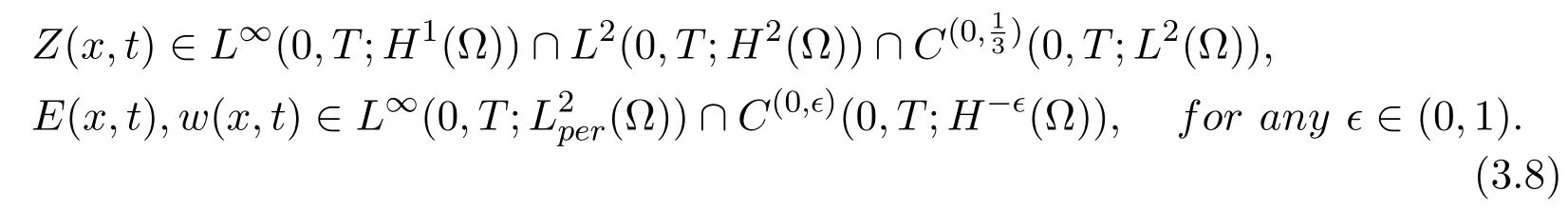
Moreover, we have

where Kj(j=0,1,2)is a constant which is independent of D.
ProofFor any vector-valued test functionwithφ(x,t)|t=T=0, we define an approximate sequence
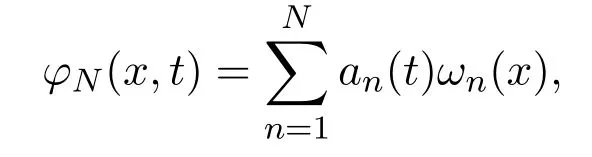
where
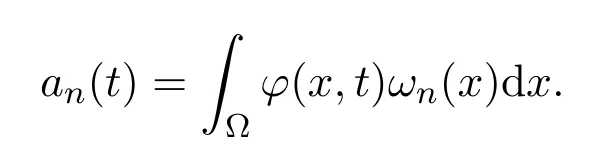
We know thatφNis uniformly convergent toφ(x,t) inthat is,
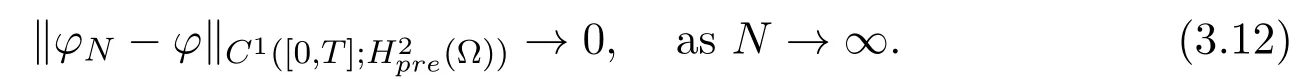
From the uniform estimates of the solution{ZN(x,t), wN(x,t), EN(x,t)}in Lemmas 2.1 and 2.2, by the Sobolev imbedding theorem and Lions-Aubin lemma, it yields that there exists a subsequence, which is still denoted by{ZN(x,t),wN(x,t),EN(x,t)}, such that
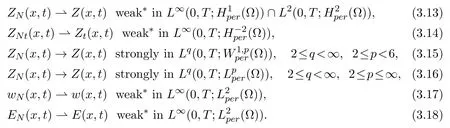
Making the scaler product ofas(t) with (2.6), the scaler product ofas(t) with(2.7), the scaler product of eσtaswith (2.8), and summing up the products with respect tos=1,2,··· ,N, we get

Rewriting (3.19), we get
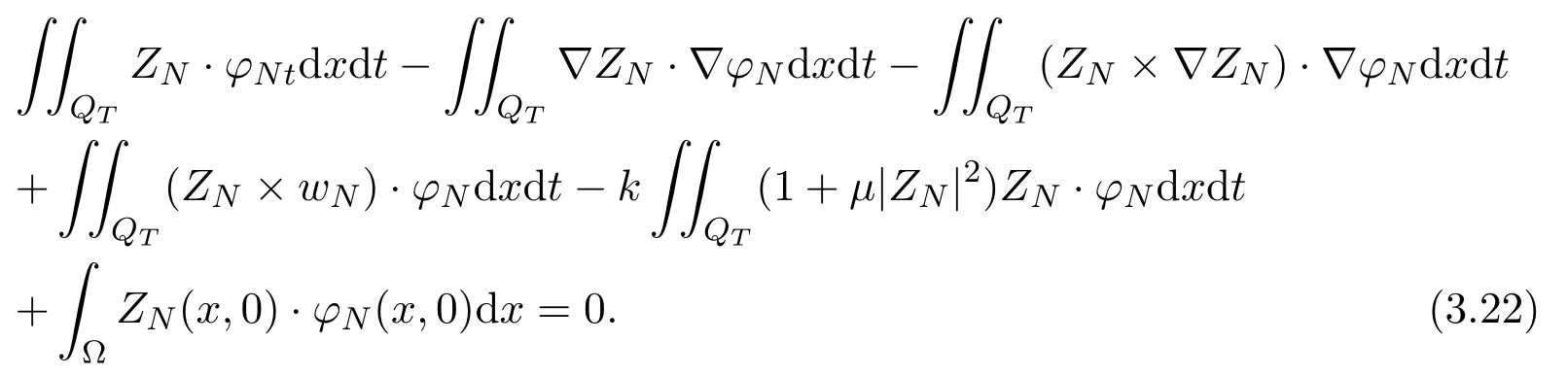
Rewriting (3.20), we get
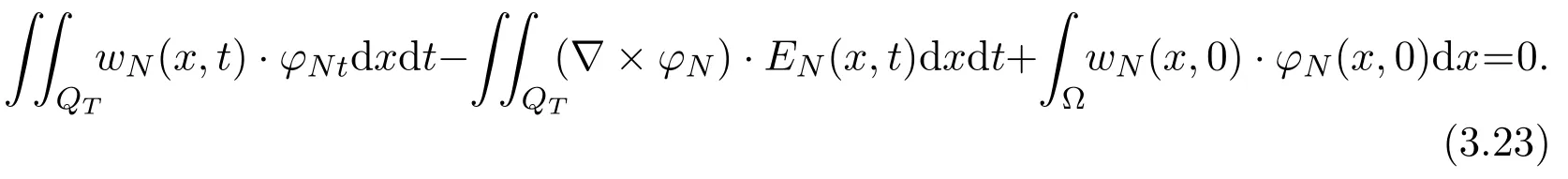
Rewriting (3.21), we get
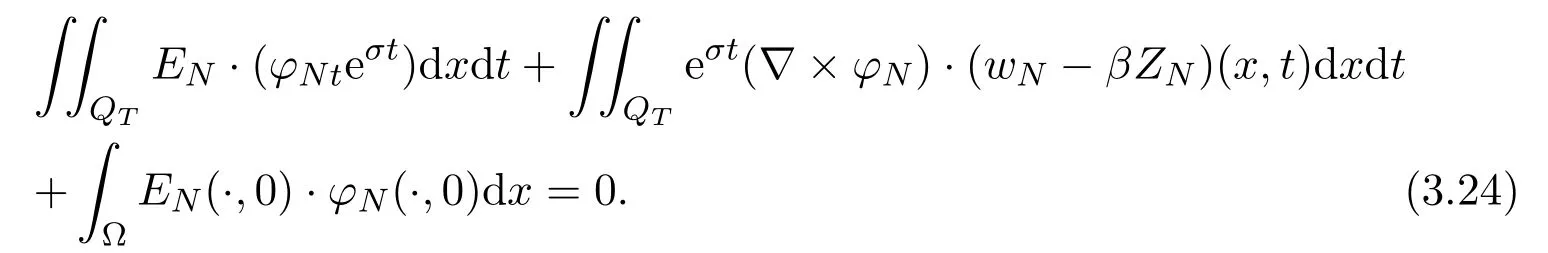
(2.2)-(2.4) and (3.12) imply that
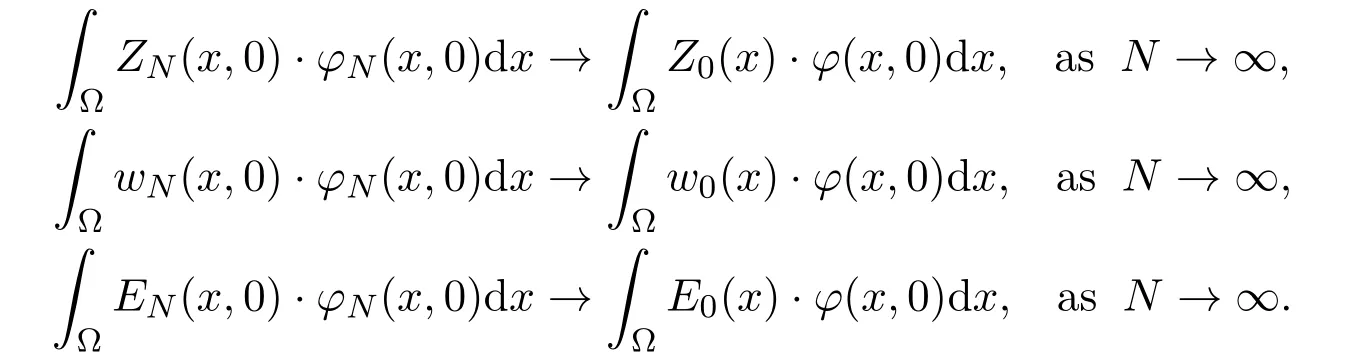
Note that
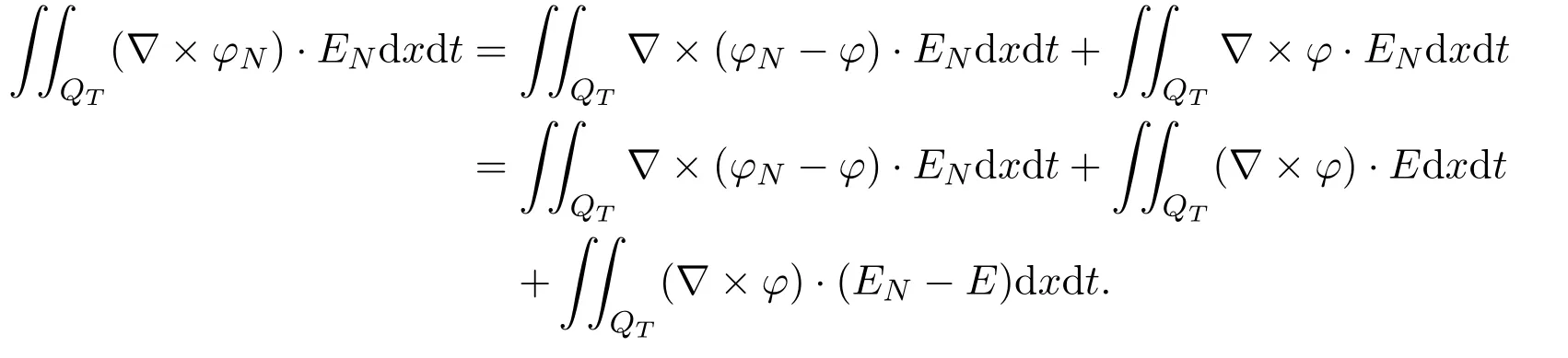
(3.12) means that
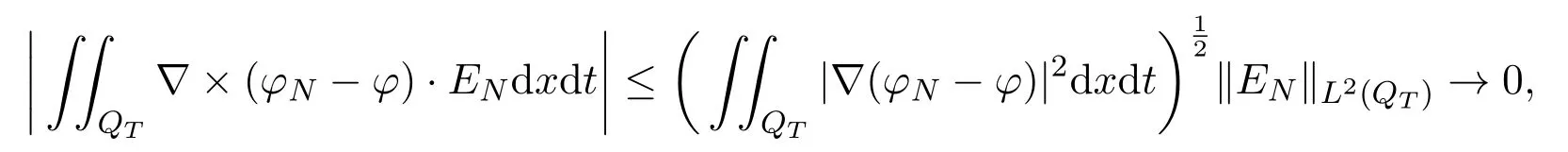
asN →∞. (3.18) implies that
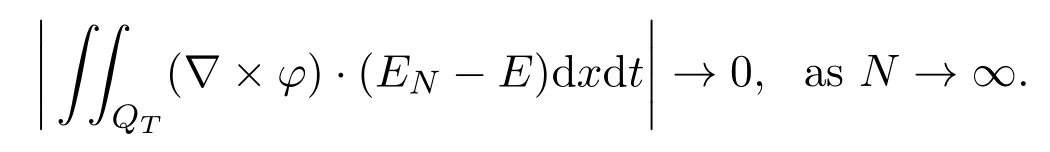
Therefore we have
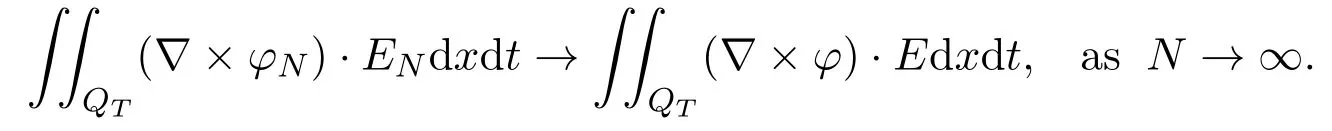
Similarly we can prove that
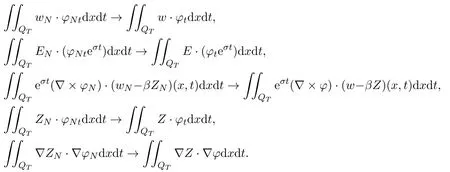
as→∞. (3.15) (3.16) and (3.12) imply that
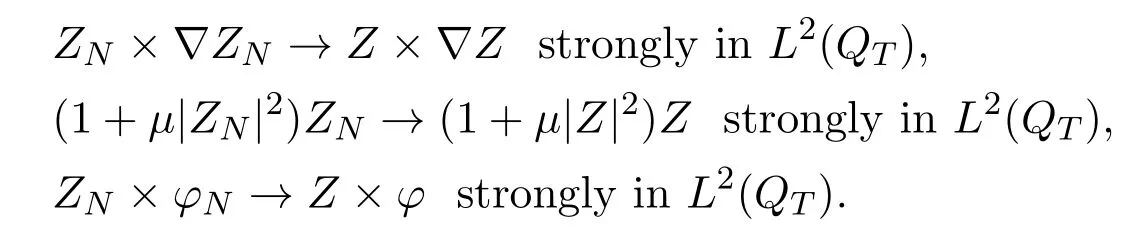
Thus we obtain that
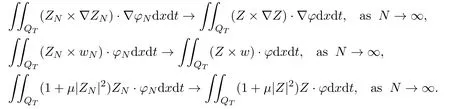
Therefore, takingN →∞in (3.22)-(3.24), we obtain that the limit functionsZ(x,t),w(x,t),E(x,t) satisfy the integral equalities (3.1)-(3.3). By Lemma 3.2,equations(3.4)(3.5)hold. Obviously (3.6)holds. The generalized global solution of the periodic initial value problem (1.12)-(1.17) is obtained.
Employing the proof of Lemma 2.3, we get
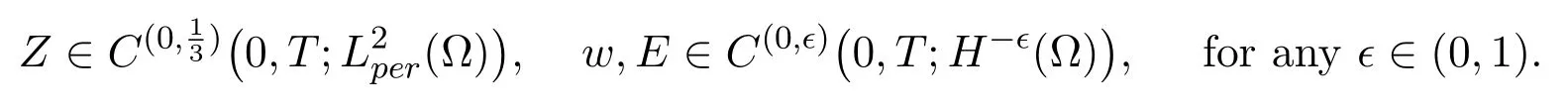
This theorem is proved.
Since a priori estimates (3.9)-(3.11) are uniform with respect toD, by using the diagonal method and lettingD →∞, we can get the following result.
Theorem 3.2Assume that Z0(x)∈H1(Rd), H0(x)∈L2(Rd), E0(x)∈L2(Rd),and(3.4)is satisfied. The constants k,σ,µ,β are positive. Then there exists a global generalized solution(Z(x,t),w(x,t),E(x,t))of the initial value problem(1.12)-(1.15) (1.17)such that
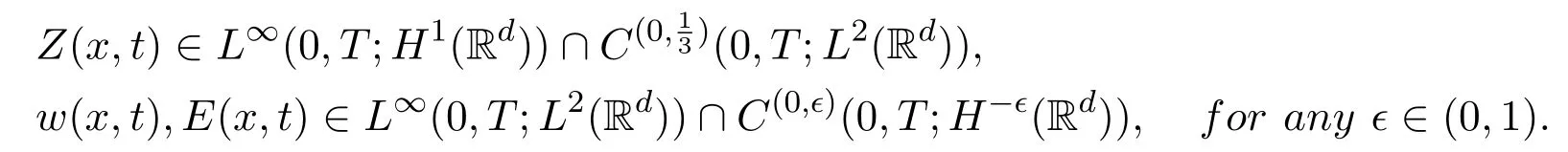
4 Regularity and Global Smooth Solution
In this section, we devote to proving the existence and uniqueness of global smooth solution to the periodic problem (1.12)-(1.17) and the initial value problem(1.12)-(1.15) (1.17). For this aim, we study the regularity of Galerkin approximate solution (ZN,wN,EN) of the problem (2.6)-(2.9).
In Subsection 4.1,we consider the case ofd=2. For this case,the global smooth solution exists and is unique no matter the size of the initial data (Z0,H0,E0).
In Subsection 4.2, we consider the case ofd=3. For this case, we only establish the existence and uniqueness of global smooth solution provided∥Z0∥H1is small enough.
The following Gagliardo-Nirenberg inequality will be used many times.
Lemma 4.1(Gagliardo-Nirenberg Inequality)Assume that u ∈Lq(Ω), Dmu ∈Lr(Ω),Ω⊂Rn,1≤q,r ≤∞,0≤j ≤m. Then
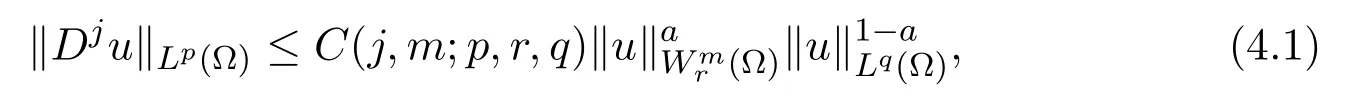
where C(j,m;p,r,q)is a positive constant, and
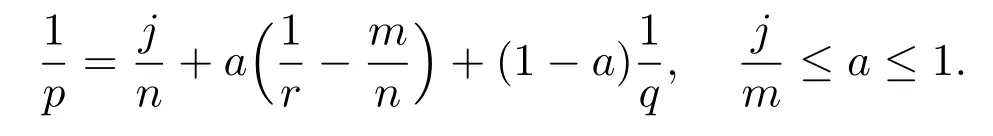
4.1 Dimension d=2
In this subsection, we consider the special case whichd= 2 andx ∈Ω⊂R2.We first establish a priori estimates of Galerkin approximate solution(ZN,wN,EN),and then prove the existence and uniqueness of the solution (Z,w,E).
Lemma 4.2Assume thatThen for the solutions of problem(2.6)-(2.9), we have
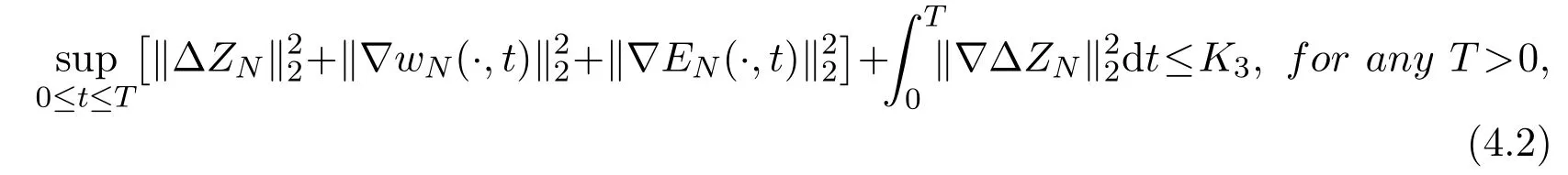
where the constant K3depends only onandand is independent of N and D.
ProofMaking the scalar product ofwith (2.6), summing the resulting equality with respect tos=1,2,··· ,N, and noting that
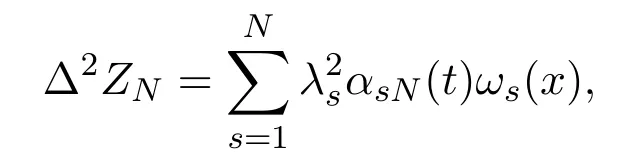
we get
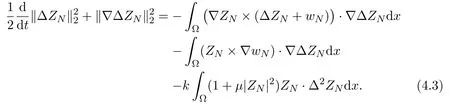
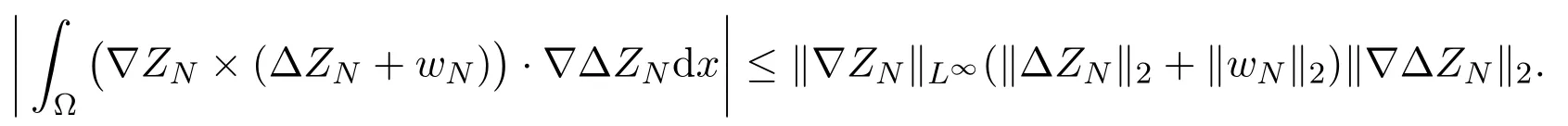
By Gagliardo-Nirenlerg inequality, we get
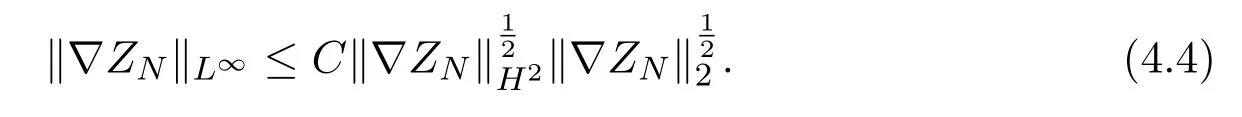
Thus, we have
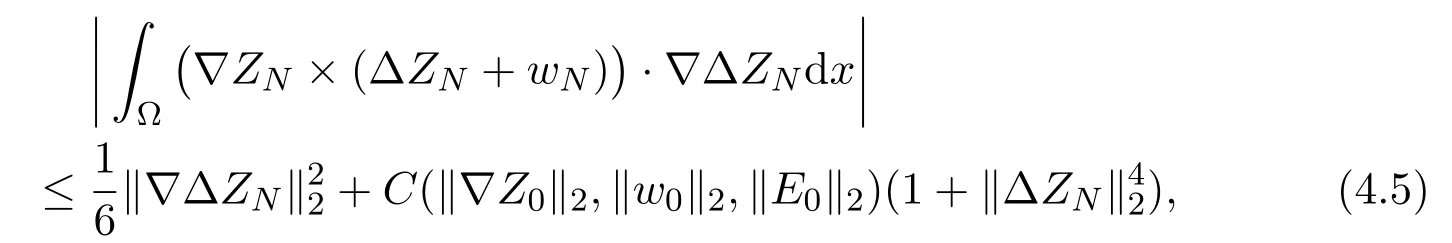
where we have used the estimate (2.12). Similarly, we get
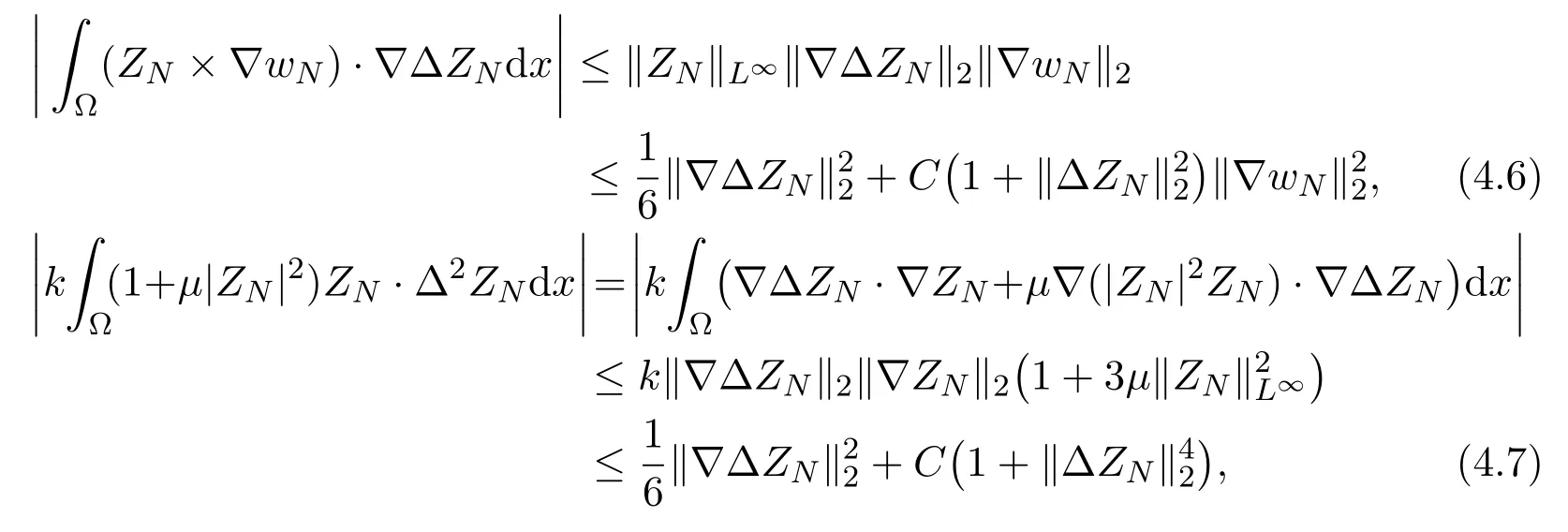
where we have used Sobolev imbedding theoremThus inserting estimates (4.5)-(4.7) into (4.3), we have
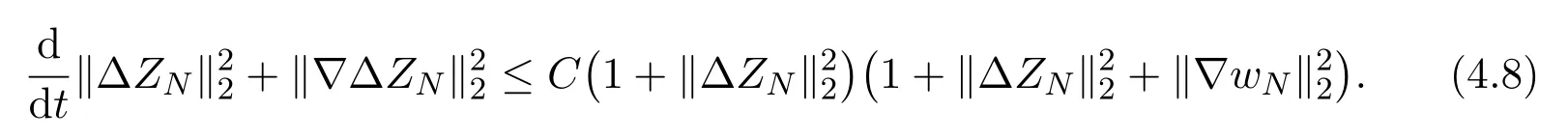
Next making the scalar product ofλsβswith (2.7) and the scalar product ofλsγswith (2.8) respectively, summing the resulting equalities with respect tos=1,2,··· ,N, and noting that
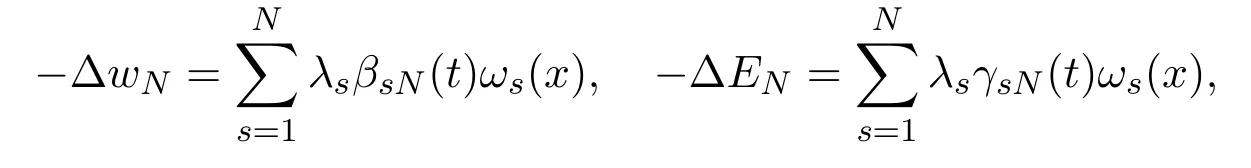
we obtain

Summing (4.9) with (4.10), we get
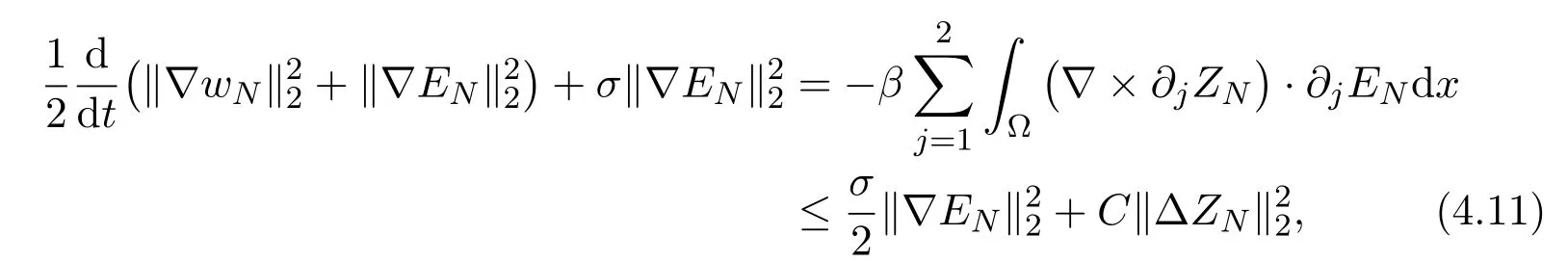
where the following fact has been used

Combining (4.8) and (4.11) we have
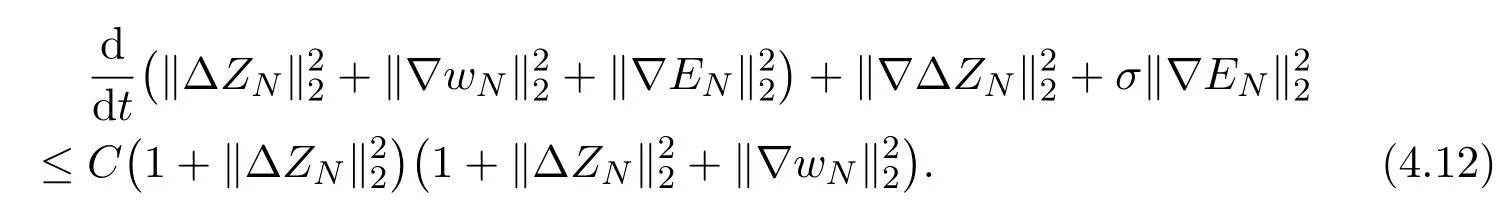
By using estimates (2.13) (4.12) and applying Gronwall inequality, we can prove estimate (4.2).
By the induction form, we can prove the following lemma.
Lemma 4.3Assume that(m ≥0), then the solutions(ZN(x),wN(x),EN(x))of the problem(2.6)-(2.9)satisfy the following estimate
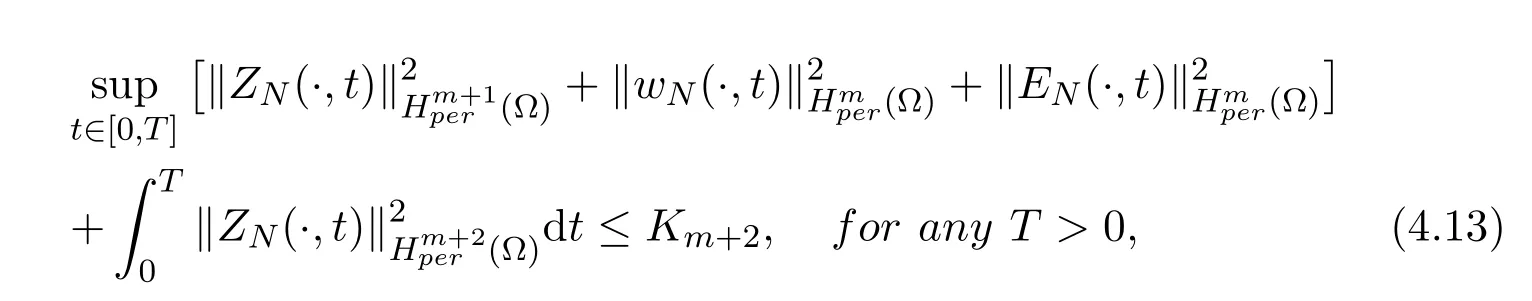
where the constant Km+2is independent of D and N.
ProofFrom Lemmas 2.1 and 4.2, the estimate (4.13) is verified form=0,1.
Making the scalar product ofwith (2.6), summing the resulting equality with respect tos=1,2,··· ,N, and noting that
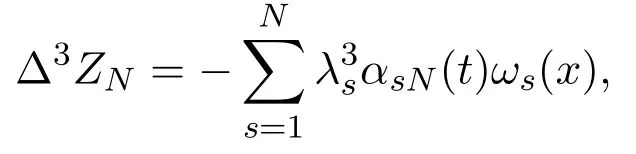
we get
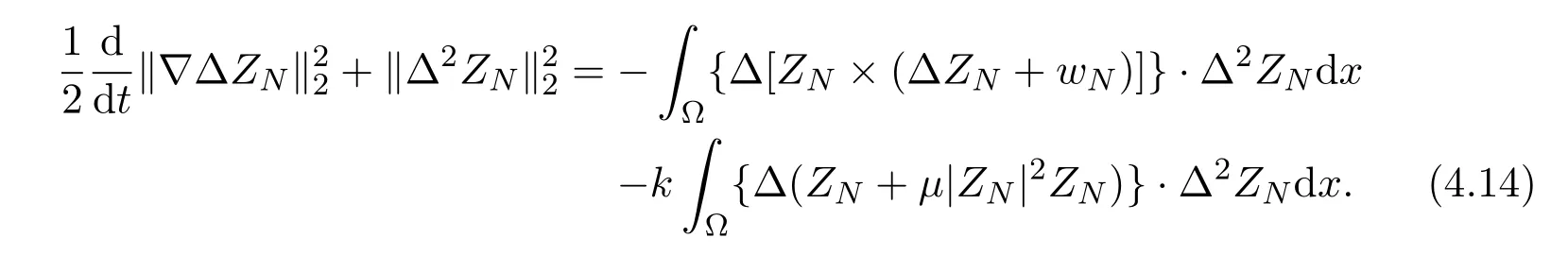
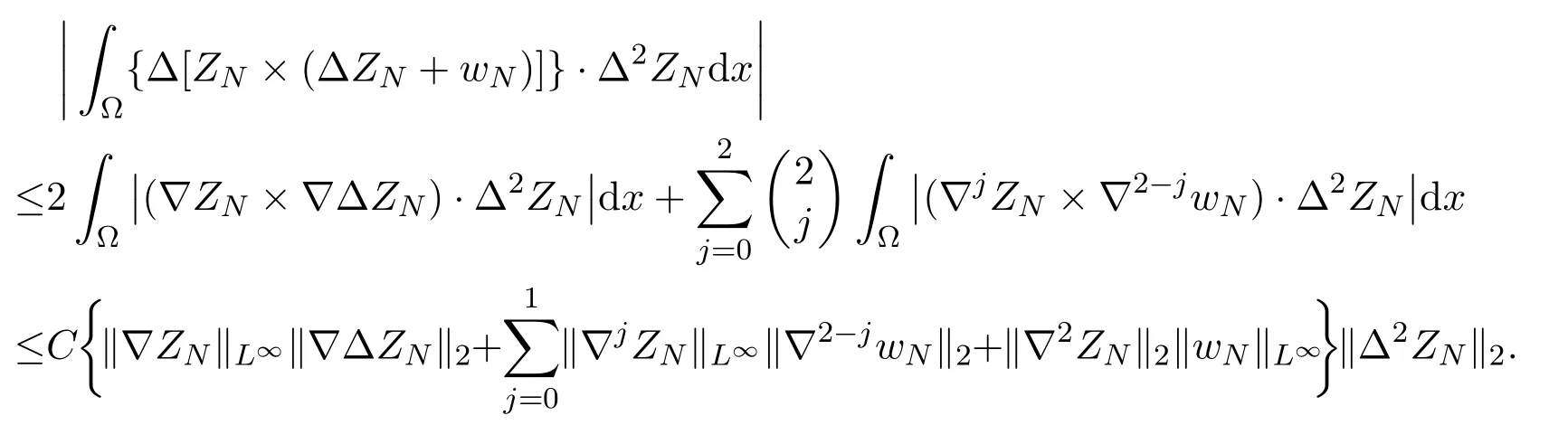
Using Sobolev imbedding theorem and the estimate (4.2), we get
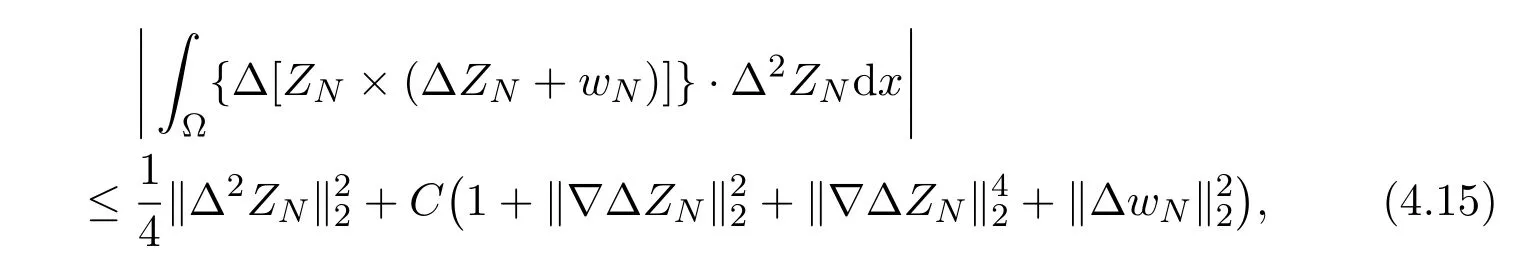
where we have used Sobolev imbedding theoremSimilarly, we get
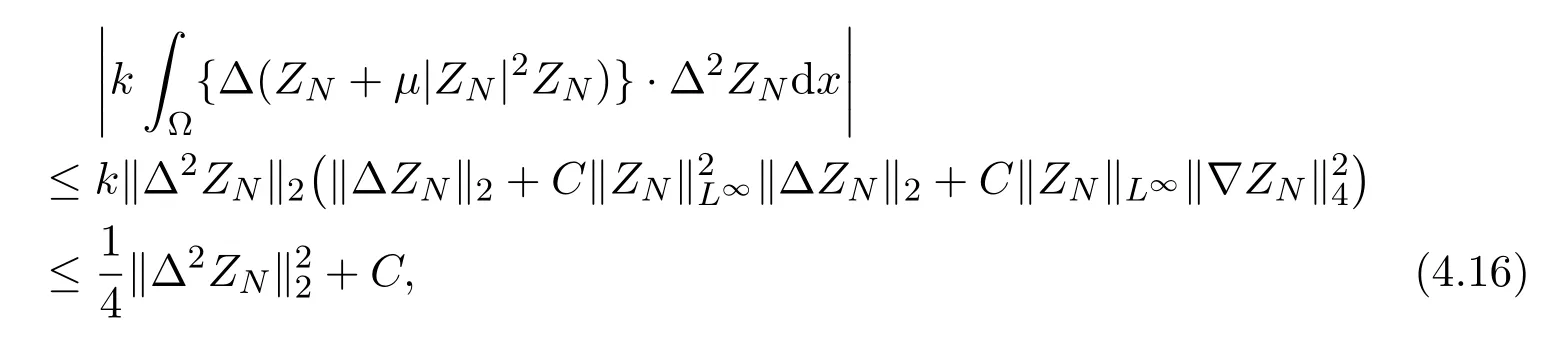
where we have used the estimate(4.2), and Sobolev imbedding theoremsThus inserting estimates (4.15) (4.16) into (4.14),we have
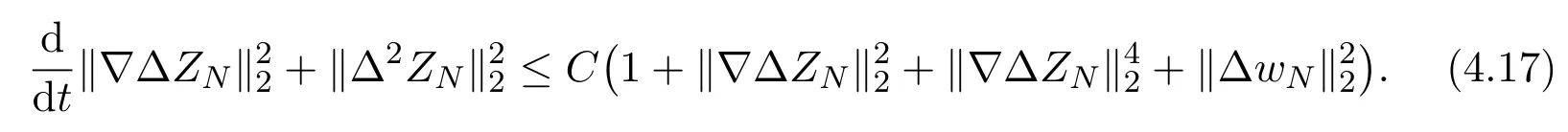
Making the scalar product ofwith(2.7)and the scalar product ofwith(2.8) respectively, summing the resulting equalities with respect tos=1,2,··· ,N,and noting that
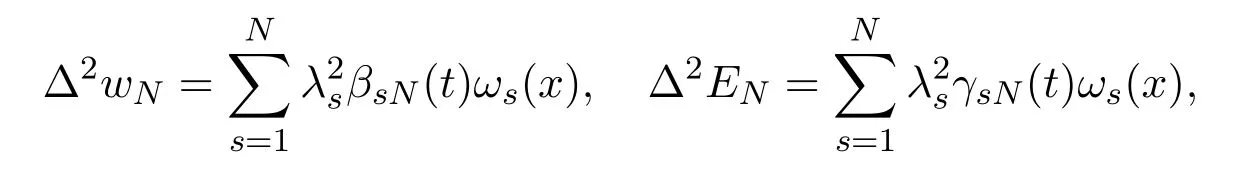
we obtain

Summing (4.18) with (4.19), we get
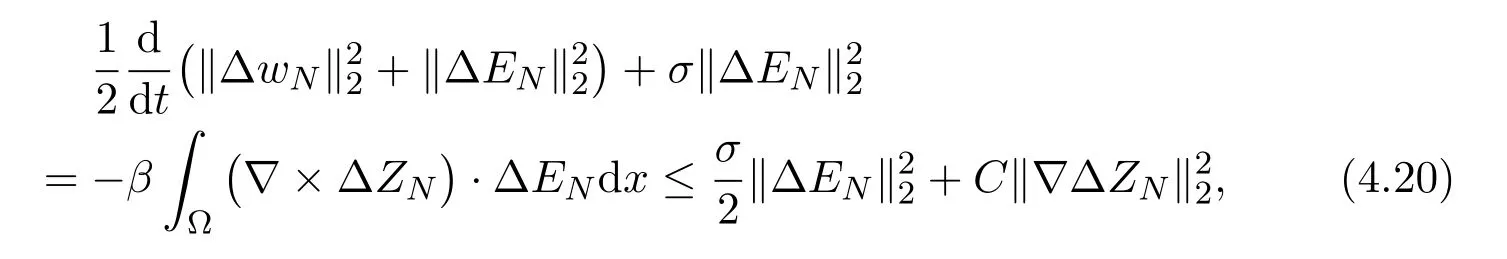
where the following fact has been used

Combining (4.17) and (4.20) we have
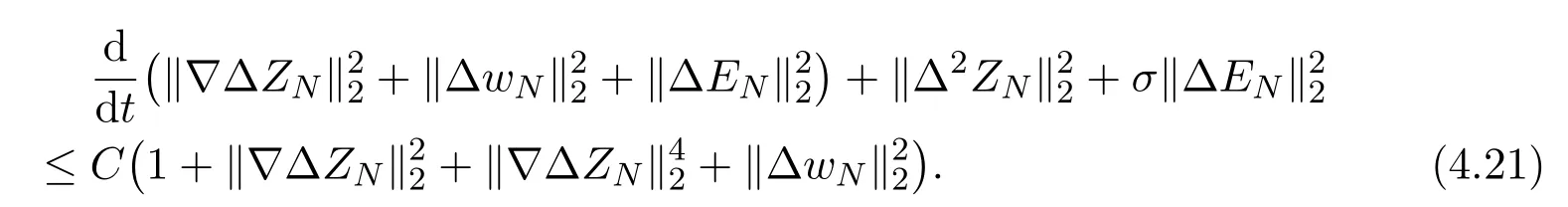
Using estimates (4.2) (4.21) and applying Gronwall inequality, we get

where the constantK4is independent ofNandD.
Now assume that the estimate (4.13) is valid form=M ≥2, that is, we have
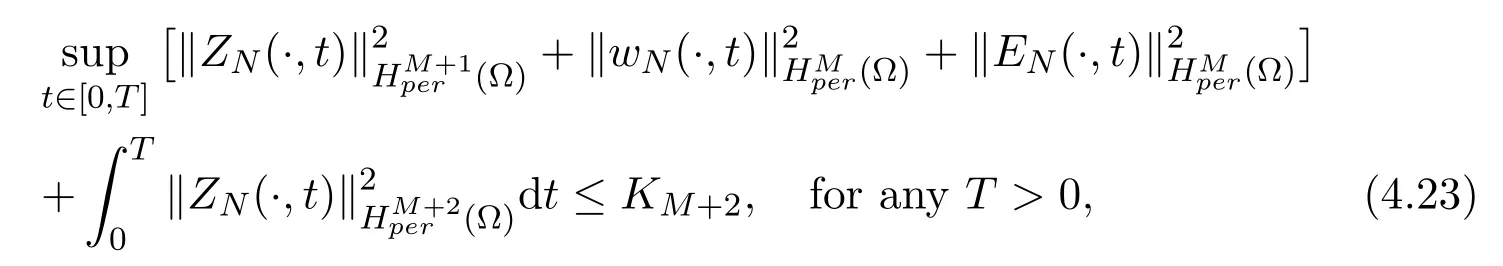
where the constantKM+2is independent ofNandD. Next we will prove (4.13)withm=M+1.
Making the scalar product ofwith(2.6),summing the resulting equality with respect tos=1,2,··· ,N, and noting that
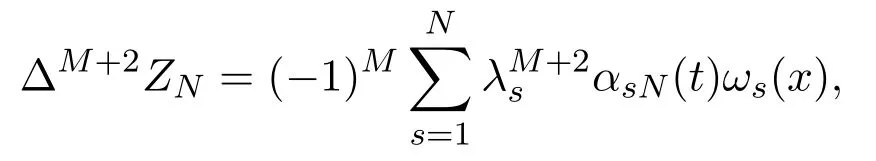
we get
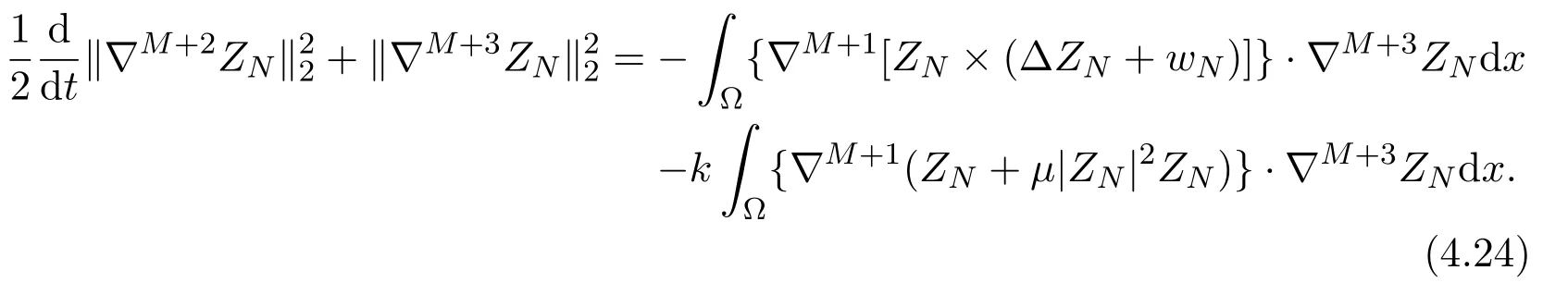

where the characteristic function
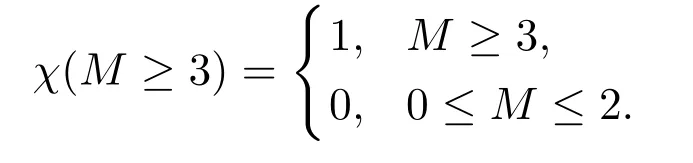
Using Sobolev imbedding theorems and the estimate (4.23), we get
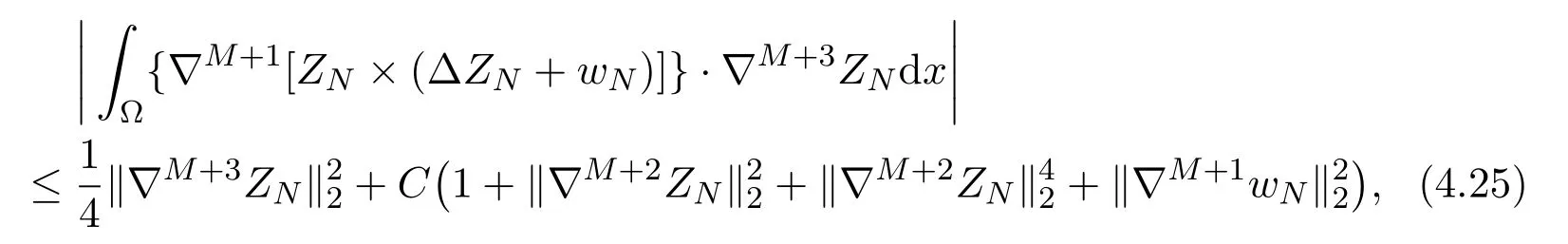
where we have used Sobolev imbedding theorems
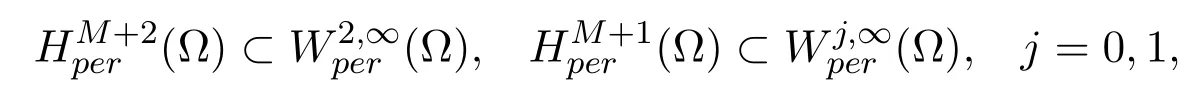
and
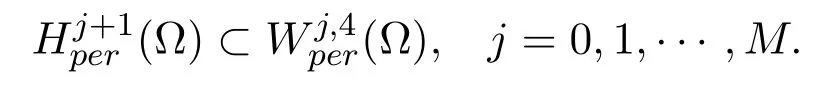
Similarly, we have
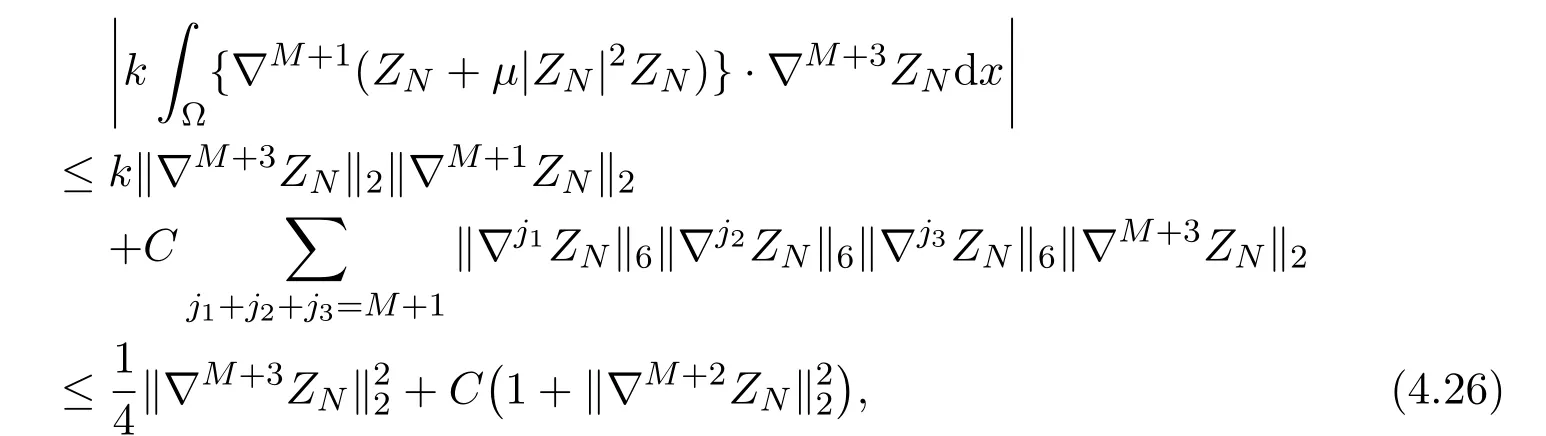
where we have used the estimate (4.23) and Sobolev imbedding theorems
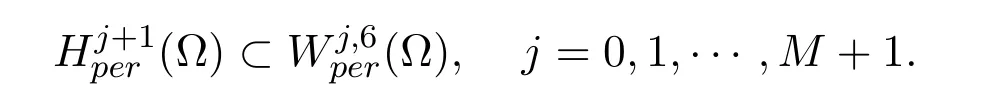
Thus inserting estimates (4.25) (4.26) into (4.24), we obtain
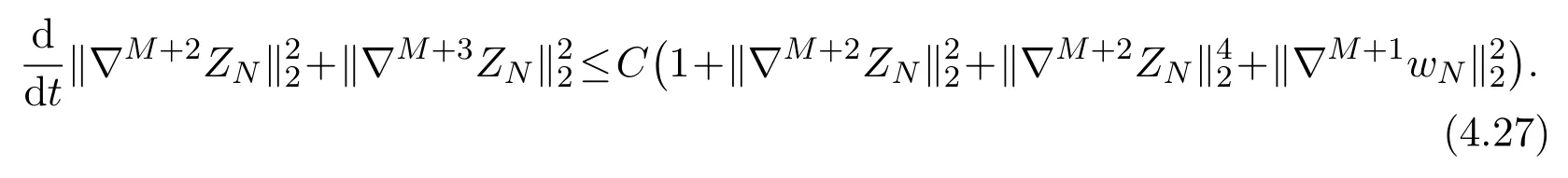
Making the scalar product ofwith (2.7) and the scalar product ofwith (2.8) respectively, summing the resulting equalities with respect tos=1,2,··· ,N, and noting that
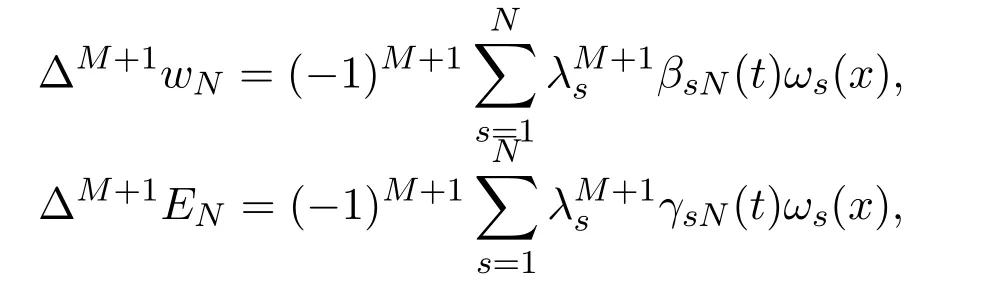
we obtain
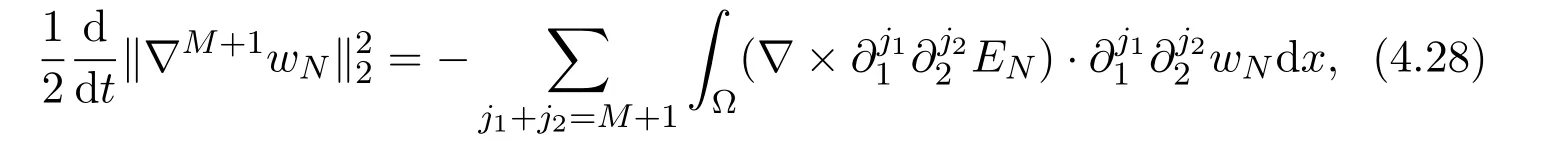
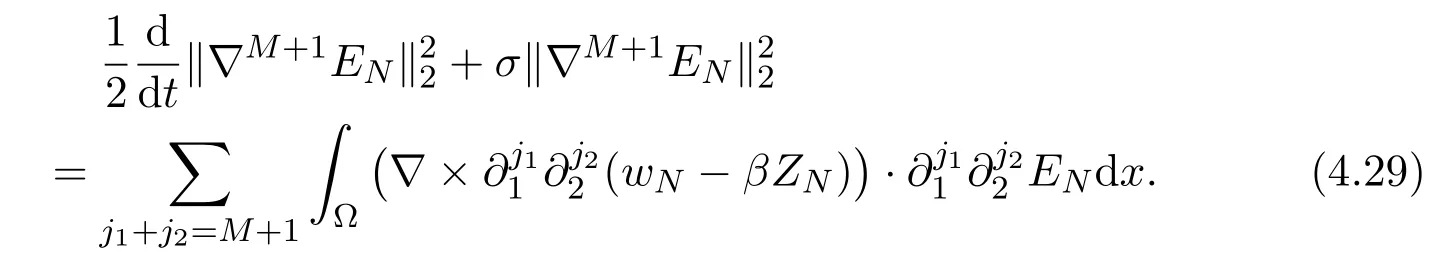
Summing (4.28) with (4.29), we get
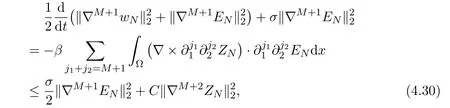
where the following fact has been used
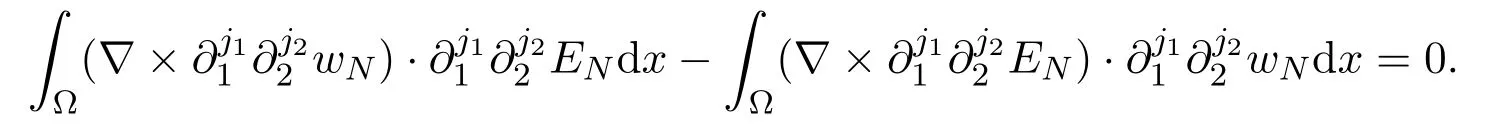
Combining (4.27) and (4.30) we have
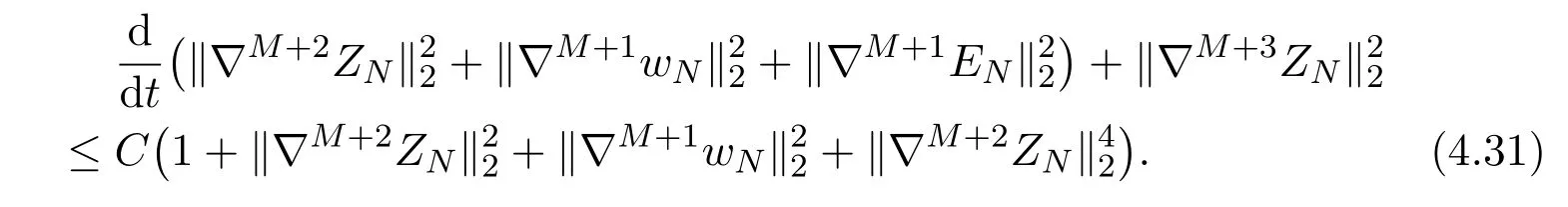
Using estimates (4.23) (4.31) and applying Gronwall inequality, we establish the estimate (4.13) withm=M+1.
By the induction, this lemma is proved.
Thanks to that the estimate (4.13) is uniform with respect toN, letN →∞,we obtain the following result.
Theorem 4.1Assume that d=2,Ω⊂R2, k,µ,σ,β >0,(Z0(x),H0(x),E0(x))Thenthere exists a unique global solution(Z,w,E)of the periodic initial value problem(1.12)-(1.17). Moreover, we have
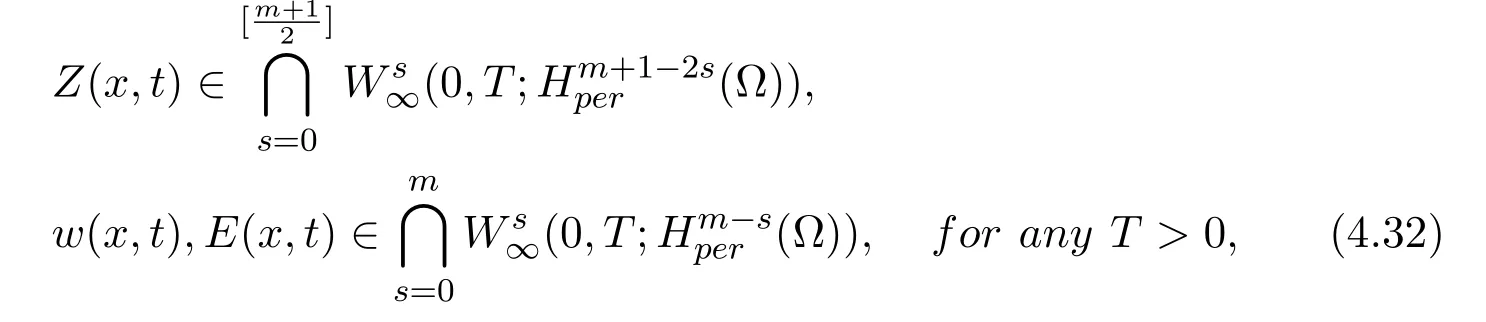
and
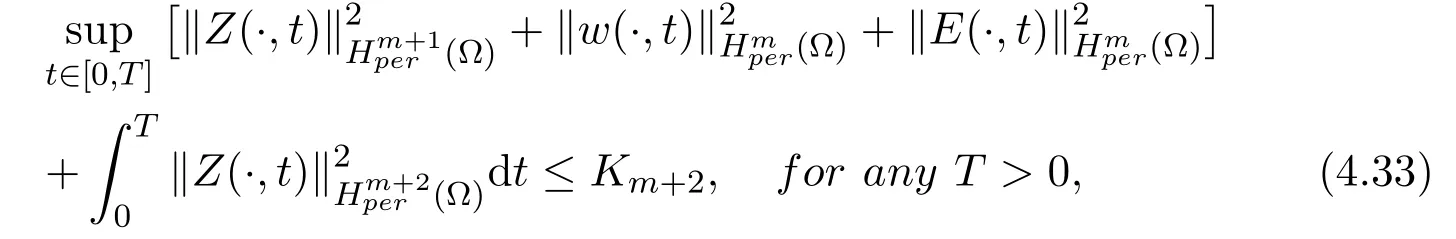
where the constant Km+2is independent of D.
ProofSimilar to the proof of Theorem 3.1,letN →∞,we can prove that there exists a global solution
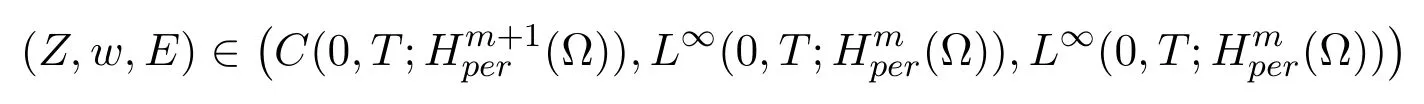
of problem (1.12)-(1.17), and the estimate (4.33) holds. The result (4.32) can be proved by using equations (1.12)-(1.14).
Now we devote to proving the uniqueness. Assume that there exist two solutions(Zj,wj,Ej) (j= 1,2). Let (φ,ψ,ξ) = (Z1−Z2,w1−w2,E1−E2), then (φ,ψ,ξ)satisfies the following equations

Making the scalar product of equation (4.34) withφ −∆φ, we have

By using Gagliardo-Nirenberg inequality, one has
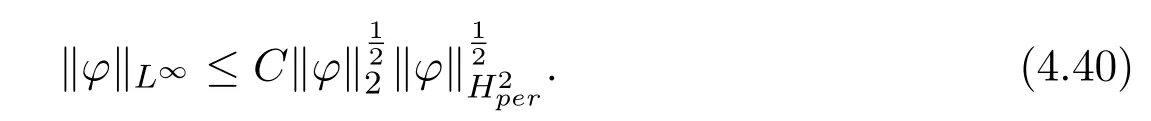
Applying the estimate (4.33) withm ≥1 and inequality (4.40), we get
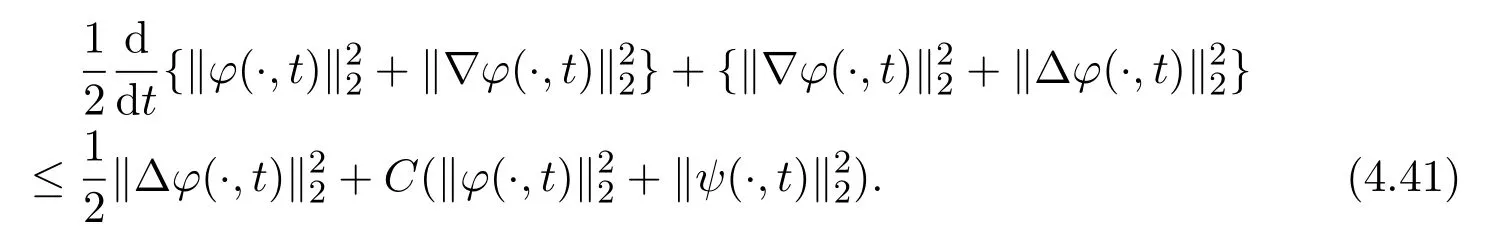
Next making the scalar product of equation(4.35)withψ,and the scalar product of equation (4.36) withξ, we have
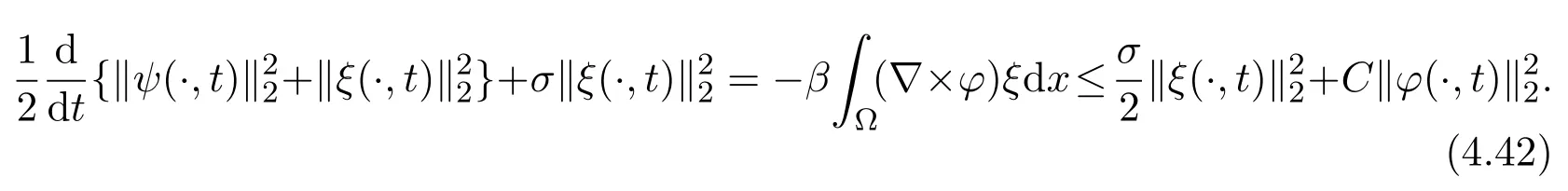
Summing (4.41) with (4.42) and applying Gronwall inequality, we get
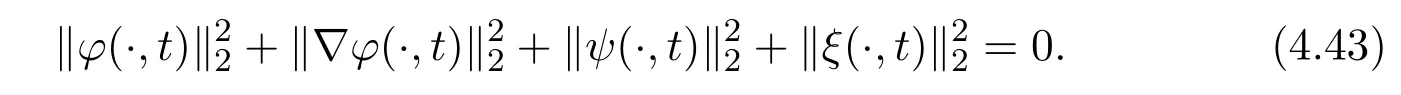
Therefore the global solution (Z,w,E) is unique form ≥1.
This theorem is proved.
Since a priori estimate(4.33)is uniform with respect toD,by using the diagonal method and lettingD →∞, we can get the following result.
Theorem 4.2Assume that d= 2, k,µ,σ,β >0,(Z0(x),H0(x),E0(x))∈(Hm+1(R2), Hm(R2), Hm(R2)), m ≥1, ∇(H0+βZ0)=0, ∇·E0=0. Then there exists a unique global solution(Z,w,E)of the initial value problem(1.12)-(1.15)(1.17). Moreover, we have

and
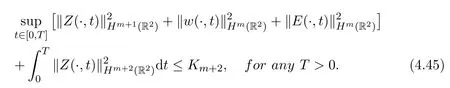
4.2 Dimension d=3
In this subsection, we consider the special case whend= 3 andx ∈Ω⊂R3.We first establish a priori estimates of Galerkin approximate solution(ZN,wN,EN),and then prove the existence and uniqueness of the solution (Z,w,E).
Lemma 4.4Assume thatσ, β µ and k are positive constants. Then for any T >0, there exists a positive constant δ0≪1such that if

the solutions of problem(2.6)-(2.9)satisfy the following estimate
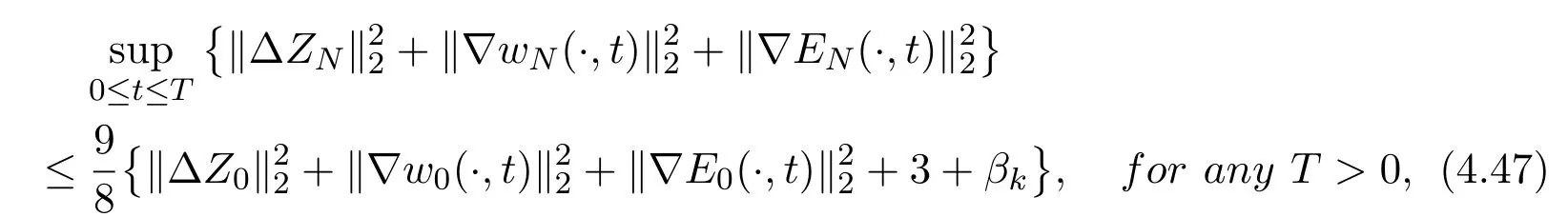
where constant
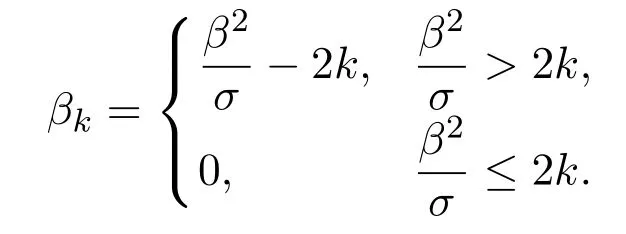
ProofRepeating the proceeding of the proof of Lemma 4.2 and revising some estimates, we can prove this lemma. In fact, the estimates (2.14) and (2.19) imply that
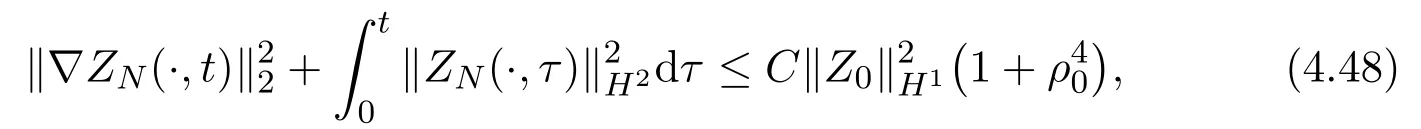
whereThe estimate (4.4) is replaced by
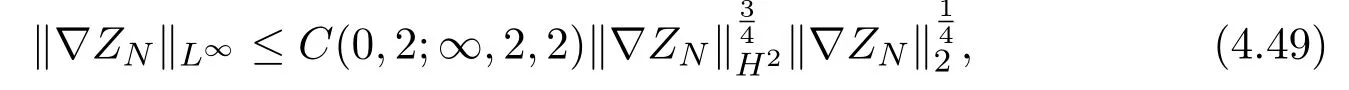
and the estimate (4.5) is reformulated by
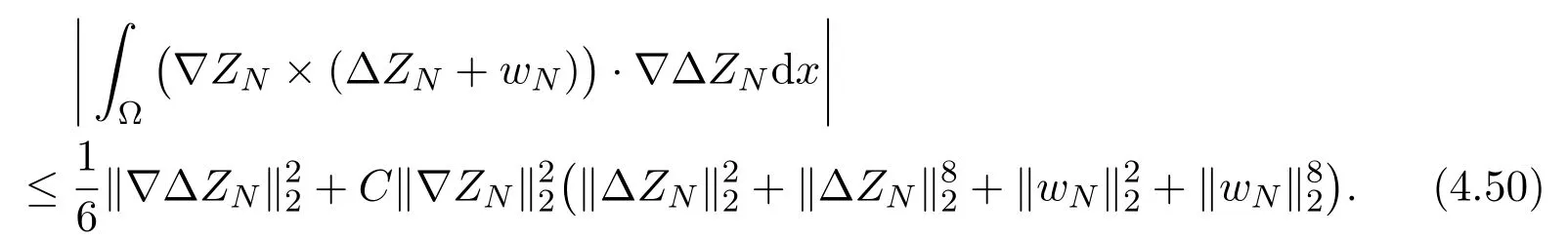
Similarly, the estimate (4.6) is replaced by

the estimate (4.7) is reformulated by
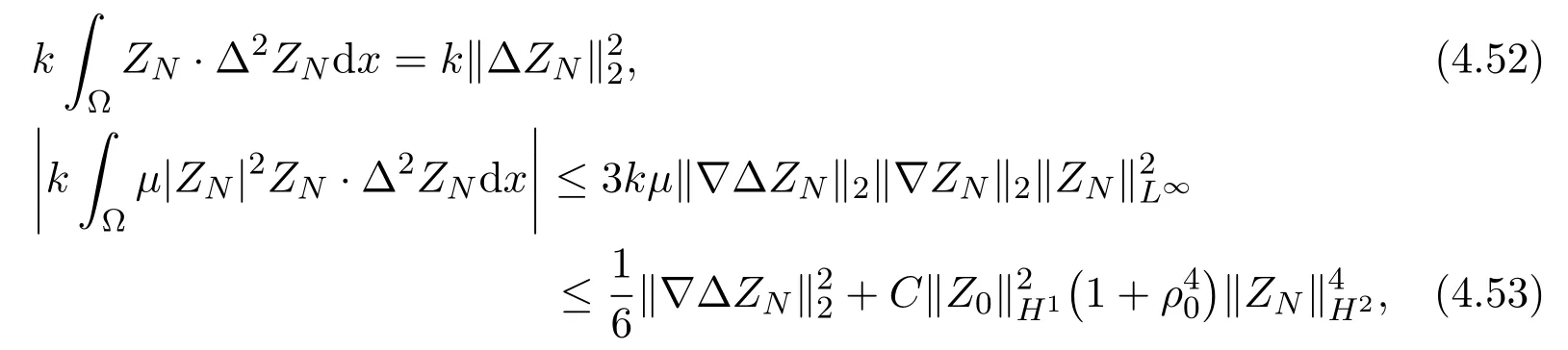
the estimate (4.8) is replaced by
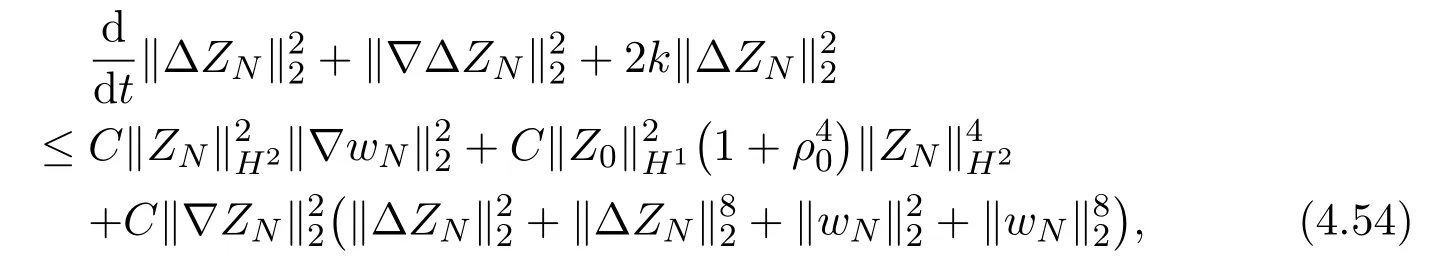
the estimate (4.11) is replaced by

and the estimate (4.12) is reformulated by

Integrating(4.56)with respect totfrom 0 toT,and using the estimate(2.15)(4.48),we have
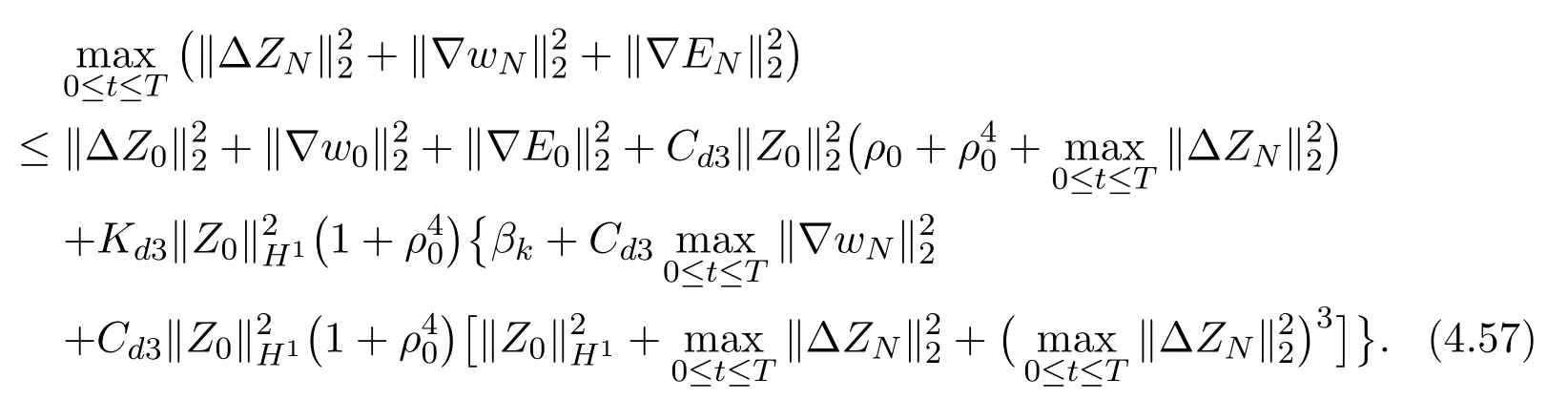
Takeδ0>0 small enough and letsuch that
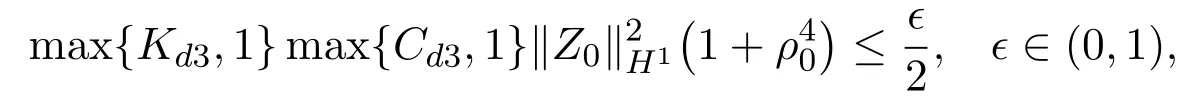
where
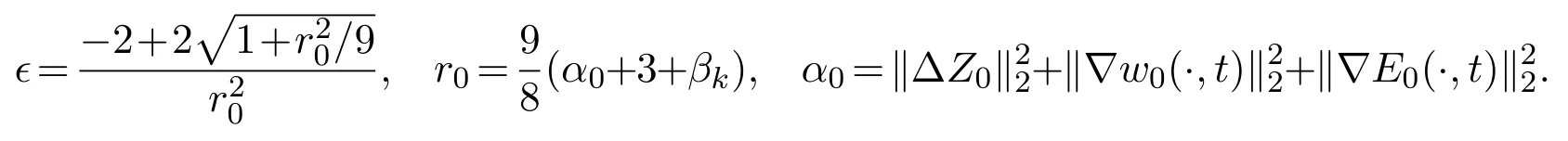
Thus we get
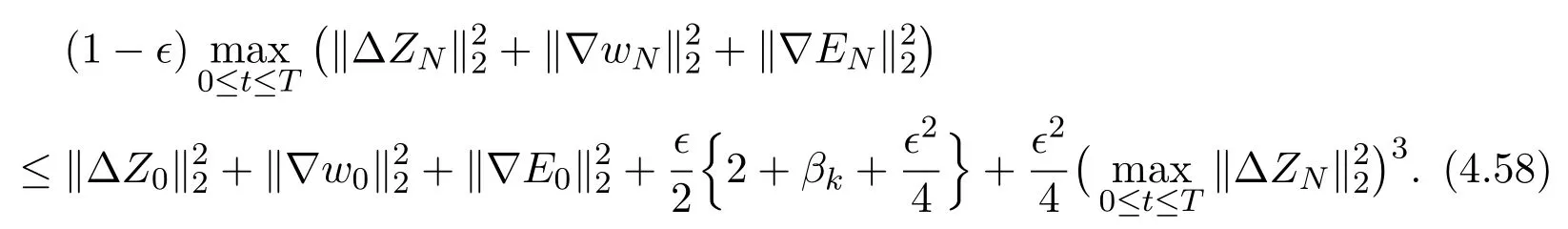
Consider the polynomial
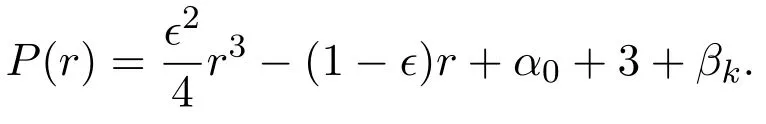
We find the fact that

Thanks to

there exists anr1>0 such that

Since(ZN(x,t),wN(x,t),EN(x,t))is continuous with respect tot, we have that

is continuous with respect toT, and
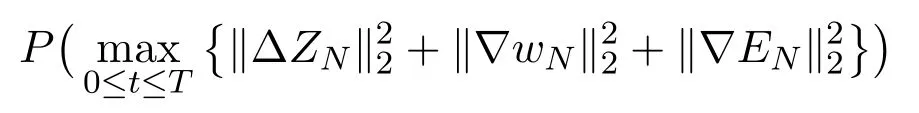
is also continuous with respect toT. Therefore the facts (4.58) (4.59) (4.60) mean that the estimate (4.47) is valid.
This lemma is proved.
Using Lemma 4.4, Lemma 4.3 can be proved whend= 3. Now repeating the proceeding of the proofs of Theorems 4.1 and 4.2, we obtain the following results.
Theorem 4.3Assume that d=3,Ω⊂R3, k,µ,σ,β>0,(Z0(x),H0(x),E0(x))∈and thereexists a positive constant δ0≪1such thatThen there exists aunique global solution(Z,w,E)of the periodic initial value problem(1.12)-(1.17).Moreover, we have
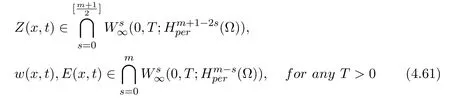
and
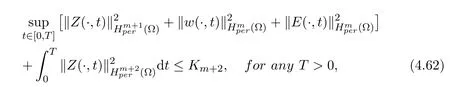
where the constant Km+2is independent of D.
Theorem 4.4Assume that d= 3, k,µ,σ,β >0,(Z0(x),H0(x),E0(x))∈(Hm+1(R3), Hm(R3), Hm(R3)), m ≥1, ∇(H0+βZ0) = 0, ∇·E0= 0, and thereexists a positive constant δ0≪1such thatThen there existsa unique global solution(Z,w,E)of the initial value problem(1.12)-(1.15) (1.17).Moreover, we have
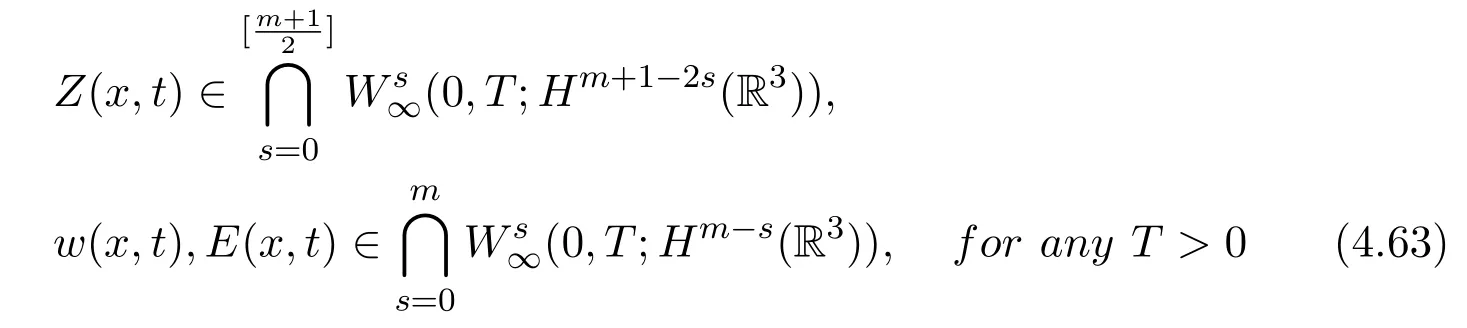
and
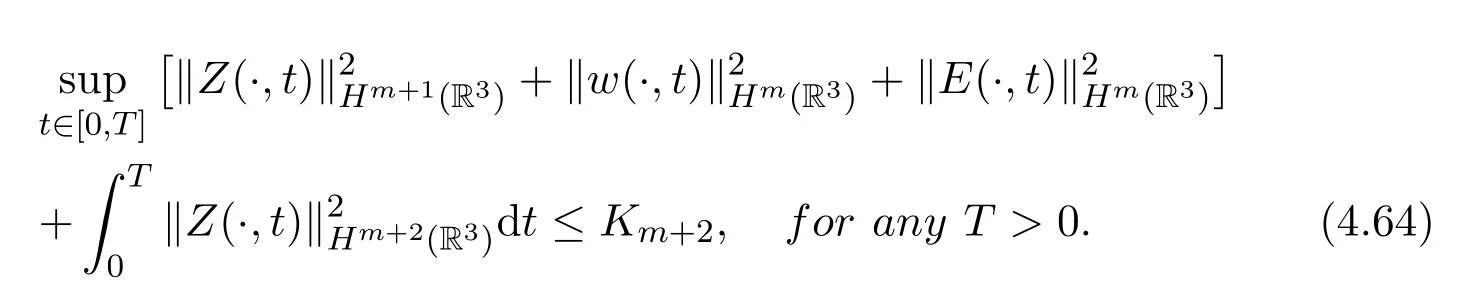
杂志排行
Annals of Applied Mathematics的其它文章
- INFORMATION FOR AUTHORS
- A FAST AND HIGH ACCURACY NUMERICAL SIMULATION FOR A FRACTIONAL BLACK-SCHOLES MODEL ON TWO ASSETS∗†
- HOPF BIFURCATION ANALYSIS IN A MONOD-HALDANE PREDATOR-PREY MODEL WITH THREE DELAYS∗
- LONG-TERM DYNAMIC ANALYSIS OF ENDANGERED SPECIES WITH STAGE-STRUCTURE AND MIGRATIONS IN POLLUTED ENVIRONMENTS∗†
- AN EFFECTIVE DETAILED ROUTING ALGORITHM CONSIDERING ADVANCED TECHNOLOGY NODES∗
